双线重载铁路路基动力响应规律研究

董俊利，冷伍明，2，徐 方，2，张期树，杨 奇，刘思慧

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

重载铁路具有运量大、能耗低、排放少、污染小等优点,是环境友好型的运输方式,也是世界铁路货运发展的总体趋势。路基占重载铁路线路的比重一般超过70%[1],其不仅要承受轨道结构重量,还需承受重载列车荷载的反复作用。随着货运重载化(大轴重、长编组、高行车密度)的持续发展,线路振动响应增强,对路基的服役性能提出了更高的要求。因此,研究重载铁路路基的动力响应具有重要现实意义。

模型试验、现场试验与数值仿真分析是研究铁路路基动力响应特性的主要方法。Momoya等[2]和Ishikawa等[3]基于缩尺(1∶5)模型试验,发现定点循环加载无法真实反映列车移动荷载下路基的长期变形特性。Shear等[4]采用“M”波模拟列车荷载,开展1∶3的缩尺模型试验,发现轨枕振动存在临界加速度使得路基沉降显著增大。Li等[5]开展现场试验采集了重载线路钢轨、轨枕、路基面和坡面的加速度,分析了振动响应沿路基面和坡面的传播特性。Liu等[6]通过大量监测数据的对比分析,发现重载列车运行下路基面动应力沿横向的衰减速率低于客运列车运行的工况。肖世伟等[7]基于大秦重载铁路路基的现场动力响应测试指出,满载条件下,C80敞车引起的路基动应力高于机车引起的动应力。王炳龙等[8]基于沪宁铁路路基的动力响应测试与分析,指出动应力沿路基面横向呈“马鞍形”分布。聂如松等[9]开展了朔黄重载铁路路涵过渡段的现场动力测试分析,发现重载列车作用下振动能量从路肩向坡脚衰减剧烈,路基的振动频率范围为0～20 Hz。目前,既有模型试验多以小比例尺为主,试验结果难以映射到实际工况;现场试验则由于测试位置多限于路基外部轮廓,而难以获得路基内部受荷核心区域的响应特性。

随着计算机技术的快速发展,数值仿真方法在铁路路基的动力响应分析中得到了广泛应用。文献[10-11]建立双线无砟轨道路基的三维有限元模型,分析表明单向和双向运行模式下路基动应力峰值均随列车速度的增大而增大,双向运行模型下路基面的竖向动位移最大。文献[12-13]基于完全耦合的列车-轨道-路基三维模型分析,指出桩承式路基中桩的存在可有效降低路基的动力响应水平。薛富春等[14]开展了双线高速铁路轨道-路基-地基的三维有限元仿真分析,发现路基内竖向加速度最大,横向加速度最小。文献[15-16]建立了桩承式路堤三维有限元模型,发现线路竖向速度与加速度从道床顶面到地基顶面均衰减了80%。刘文劼等[17]和Mei等[18]基于车辆-轨道耦合动力学理论[19],建立了朔黄重载铁路典型路基段的三维动力有限元模型,指出列车相邻转向架通过时引起的动应力存在明显的叠加效应。

目前,关于重载铁路路基动力响应方面的研究相对落后,相关研究多局限于单线重载路基,且分析对象亦多侧重于动应力这一单一指标。然而,国内外重载线路多以双线为主[20],其运行模式与普通/高速铁路存在显著区别。以朔黄线为例,上行线为重车线,下行线为轻车线,上、下行线路基荷载存在显著差异,致使其路基动力响应有别于普通/高速铁路线路。因此,开展双线重载铁路路基动力响应特性的研究具有显著的工程意义。本文建立双线重载铁路路基的三维有限元模型,并基于实测数据完成校核,系统研究了不同轴重重载列车在双向、满载单向和空载单向3种运行模式下的路基动力响应规律。

1 数值模型

1.1 重载列车荷载的模拟方法

列车运行时,车轮作用于钢轨,并通过钢轨与轨枕间的连接与接触将重载列车荷载传递至下部的道床、路基与地基。钢轨和轨枕连接处的接触力Q(t)可视为重载列车作用于轨枕的等效荷载,因此,数值仿真分析中,可将列车荷载转换为作用于轨枕上的周期性荷载。采用图1所示的典型连续弹性支承梁模型,推导接触力Q(t)的近似解析表达式。

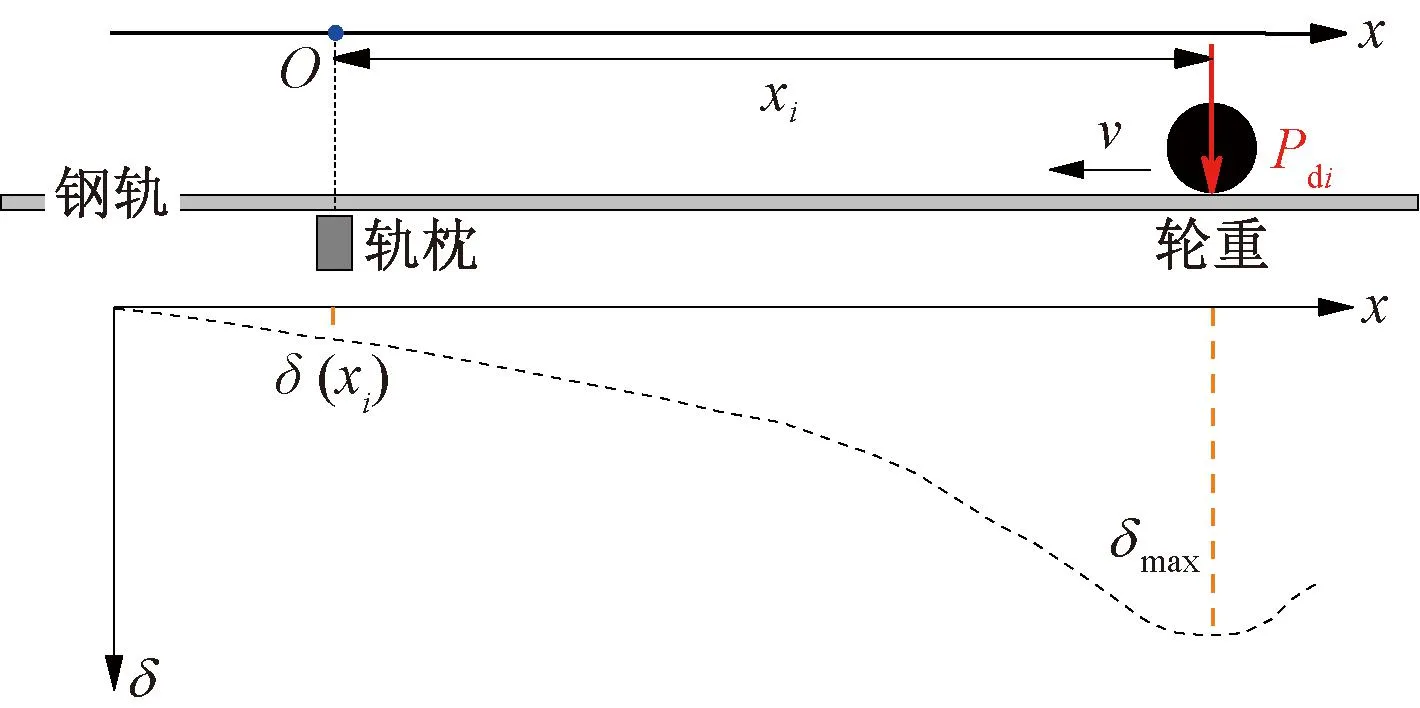
图1 钢轨与轨枕间接触力计算模型示意

图1中,钢轨视为支承于Winkler地基上的无限长Euler-Bernoulli梁。定义钢轨在动轮载Pd作用下的挠度曲线(向下为正)为δ(x),则连续支承梁模型的挠曲线微分方程[21]为

(1)

式中:EI为钢轨的抗弯刚度;u为轨道基础的弹性模量,由钢轨支座刚度D与轨枕间距a求得,u=D/a;x为目标轨枕与动轮载Pd间的距离。

引入钢轨基础与钢轨的刚比系数k,k=[u/(4EI)]1/4,则式( 1 )可转化为

(2)

式( 2 )为4阶常系数线性齐次微分方程,其边界条件为

(3)

在上述边界条件下,求解式( 1 )可得距离目标轨枕x处的动轮载Pd于目标轨枕处引起的竖向挠度,即

(4)

令φ(x)=e-k|x|[cos(kx)+sin(k|x|)],则列车运行时作用在轨枕上的钢轨压力(或轨枕反作用力)R为

(5)

动轮载Pd以匀速v在钢轨上移动,若荷载作用点与目标轨枕的初始距离为x0,经过时间t后,φ(x)的表达式为

φ(x)=φ(x0-vt)

(6)

动轮载Pd可通过静轮载P0乘以荷载放大系数获得,即

Pd=P0(1+αv+βp)

(7)

式中:αv为速度系数,αv=0.45v/100,v为行车速度;βp为偏载系数,模型中不考虑偏载情况,则βp=0。

对于多个轮载(如转向架加载),接触力Q(t)随时间的变化可通过叠加法得到

(8)

式中:n为轮对荷载数量;xi为目标轨枕与第i个轮对动荷载Pdi间的距离。

大量实测数据和理论分析表明,单个轮对荷载近似按图2所示的比例分配给临近轨枕,即单轮荷载主要由附近的5根轨枕共同承担[22]。本文建立含有5根轨枕的重载路基有限元仿真模型,并通过在5根轨枕上输入荷载时程曲线模拟列车竖向荷载。依据列车运行方向确定轮载最先到达的轨枕,若列车动轮载作用在第1根轨枕上的荷载时程曲线为F(t),则作用在其余4根轨枕上的荷载时程曲线为F(t-iΔt)。其中,i=1, 2, 3, 4;Δt=a/v。

图2 列车轮载在五根轨枕上分担示意

为探讨大轴重列车作用下双线重载铁路路基的动力响应特性,动荷载波形考虑了5节车厢。列车车型选择C80B和C96敞车,其满载轴重分别为25、30 t。敞车结构见图3,相关尺寸见表1。依据式( 8 )计算得列车运行速度v=80 km/h时,连续5节车厢通过目标轨枕的等效荷载时程曲线,如图4所示。由图4可知,等效荷载时程曲线呈“M”形分布,与聂如松等[22]和庄妍等[15]的研究结果一致,符合列车动荷载的典型分布特征;另外空载列车的等效荷载明显小于满载列车,上、下行线列车动荷载的显著差异,可能引起路基动力响应表现出不同的特性。本文重点研究不同轴重列车在3种运行模式下的双线路基动力响应规律,暂未落脚于轮轨接触和轨道不平顺的影响,因此采用上述方法对重载列车荷载进行等效模拟,避免车辆模型和轮轨接触关系的处理,以减小多工况仿真分析的计算成本。

表1 列车车型参数

图3 敞车结构参数

图4 等效荷载时程曲线

1.2 计算参数与模拟工况

本文依托朔黄铁路双线路基段工程实例,基于Abaqus软件建立双线重载路基的三维有限元仿真模型,如图5所示。其中满载列车线(上行线)为Ⅲa型轨枕,轨枕间距a=0.6 m;空载列车线(下行线)为Ⅱ-J2型轨枕,轨枕间距a=0.54 m。模型底部采用固定约束,四周边界采用无限元处理[23],以模拟无限远地基对振动波的吸收效应。图5中,X轴为线路横断面方向,Y轴为竖直方向,Z轴为线路纵向。数值仿真中模型尺寸对计算量和计算精度均有一定影响,本文建立含有5根轨枕的双线重载铁路轨枕-路基-地基三维有限元仿真模型,轨道和路堤尺寸均参照朔黄重载铁路实际工况设置,具体尺寸为:道床厚0.5 m;路堤高7.0 m,其中基床表层厚0.6 m,基床底层厚1.9 m,基床以下路基厚4.5 m;路基面宽11.96 m,路基坡率1∶1.5。

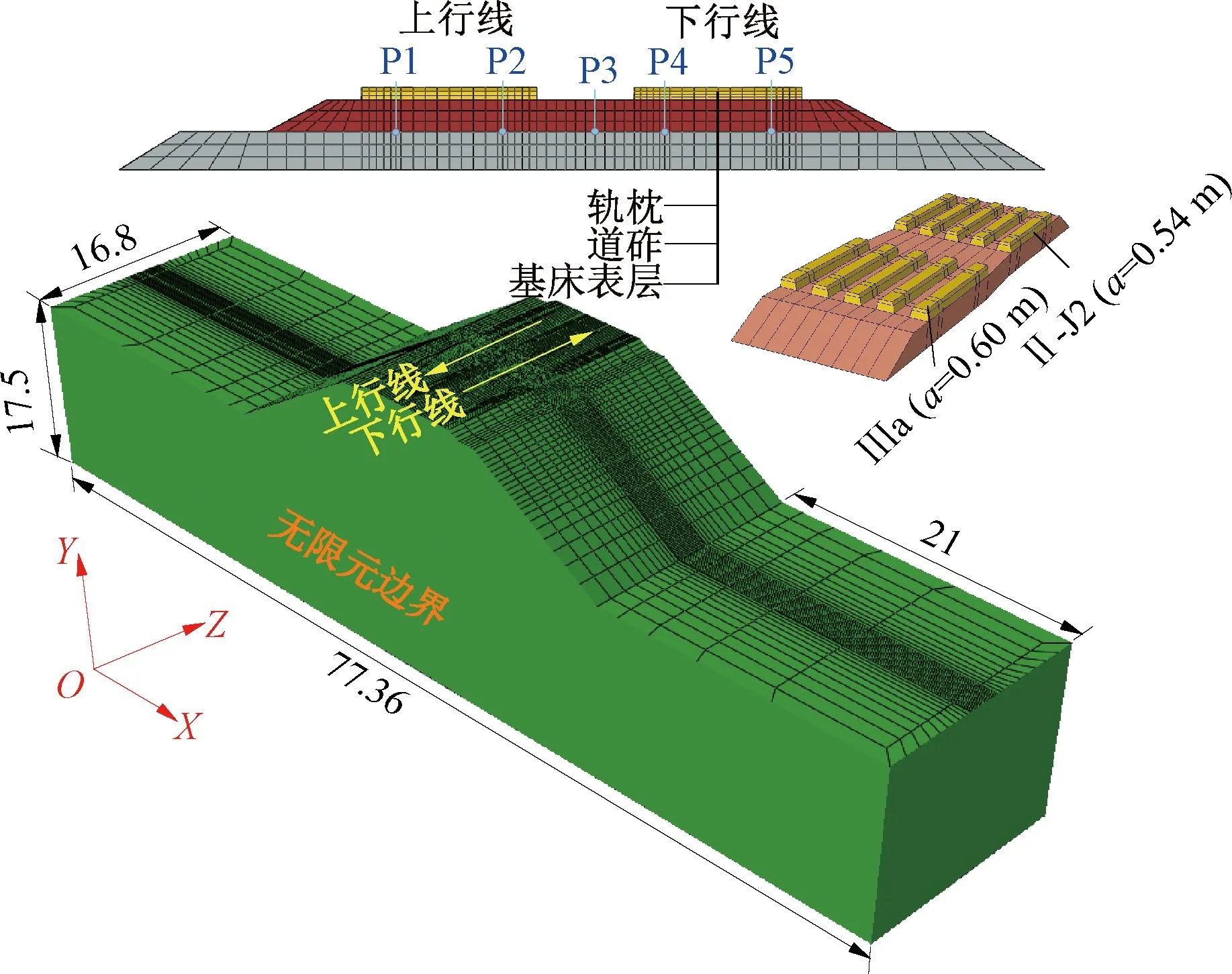
图5 双线重载铁路路基有限元网格示意(单位:m)

模型路基纵向(Z向)总长度为16.8 m,加载区前后设置有7 m过渡区,并采用无限元模拟纵向边界,消除此边界处应力波反射对仿真结果的影响。模型路基横向(Y向)边界距路基坡脚21 m,同样采用无限元模拟,以消除边界处应力波的反射效应。路基模型计算深度的设置则主要考虑路基动力响应的衰减情况;相关研究[17,22]表明,重载铁路路基面以下2.5 m深度处动应力衰减量可达60%,本文路基模型中地基深度为17.5 m,模型底部距路基面的距离达到24.5 m,满足计算要求。选取沿路基中心线对称分布的5个测点P1～P5(见图5),分析重载列车作用下路基的动力响应。其中,P1、P2位于上行线钢轨下方;P3位于线路中心;P4、P5位于下行线钢轨下方。轨枕-路基-地基耦合模型的本构参数参照朔黄重载铁路各结构层材料的相关试验结果[1],具体如表2所示。数值仿真中,考虑3种不同的运行模式:满载和空载列车双向运行及满载和空载列车分别单向运行。表3为具体仿真工况。

表2 轨道路基模型的材料参数

表3 仿真计算工况

阻尼是指振动系统受阻滞使能量随时间而耗散的物理现象。在各种阻尼形式中,Rayleigh阻尼矩阵计算方便且节约内存,并可满足一定的计算精度。Rayleigh阻尼采用质量矩阵M和刚度矩阵K的线性组合,可表示为[24]

C=αM+βK

(9)

式中:C为体系的阻尼矩阵;α为质量比例阻尼系数;β为刚度比例阻尼系数。

通常假定不同振型下阻尼比Dr为定值[25-26],在选定目标频率ω1和ω2的情况下,可利用式(11)和式(12)确定α和β,即

(10)

(11)

式中:Dr为阻尼比;ω1为模型基频;ω2为对路基系统动力响应有显著影响的高阶振型频率。

本文模型中材料的阻尼比Dr取值参考文献[1],变化范围为[0.05, 0.15]。利用Abaqus求出模型的目标频率ω1和ω2,将其代入式(11)和式(12)中可获得各结构的阻尼系数α和β,表4统计了模型中各层材料的Rayleigh阻尼参数。

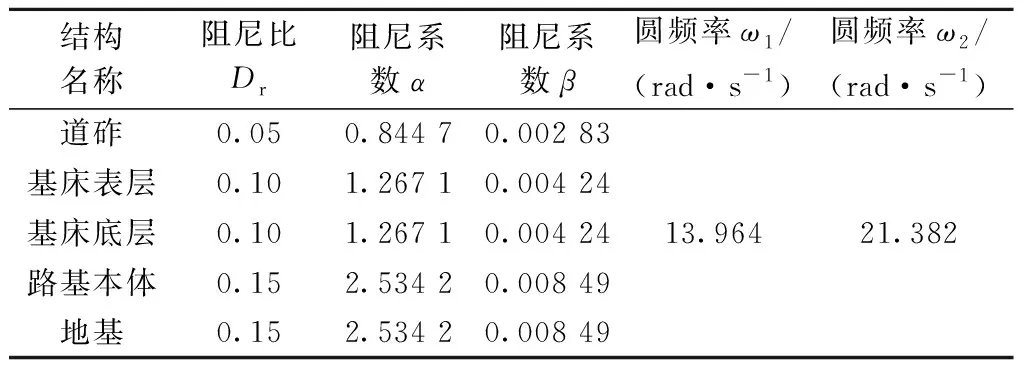
表4 模型中路基层的Rayleigh阻尼参数

2 数值模型验证

采用朔黄重载铁路现场试验工点在C80B敞车满载单向运行工况下的路基动力响应实测结果进行验证。现场试验工点及测点布置分别如图6和图7所示,采用的测试设备为891-Ⅱ型拾振器+IMC采集仪+信号放大器+便携式计算机,拾振器布置在上行线侧的路肩位置。

图6 测试系统现场布置

图7 测点布置(单位:m)

C80B敞车以运行速度v=74 km/h驶过时,测点处的竖向动位移时程曲线如图8所示。由图8可知,测点处的动位移时程曲线呈现明显的周期性;列车相邻转向架通过时,各轮对引起的动位移存在叠加效应,动位移的峰值由相邻转向架的4个轮对共同作用引起。

图8 路肩测点处动位移时程曲线

数值分析获得路肩测点位置处的竖向动位移结果与现场试验结果对比如图9所示。由图9可知,数值仿真的动位移时程曲线波形与现场测试结果类似,且峰值接近。二者差别的主要原因在于现场实地条件更加复杂,对振动波的传播存在一定影响。

图9 数值模型与现场试验的动位移对比分析

文献[27]以朔黄重载铁路为工程背景,通过模型试验测试了满载列车荷载作用下路基面的动应力响应特性。图10为C80B敞车满载单向运行条件下,本文有限元模型所得上行线路基面轨道中心处的动应力与同轴重加载条件下室内模型试验结果的对比。由图10可知,数值仿真所得竖向动应力时程曲线与试验结果较为一致,且动应力峰值十分接近。将本文仿真计算结果与文献[1, 5, 7, 27, 32-36]报道的现场实测、模型试验和数值模拟结果进行对比,发现路基同一结构层处的动力响应(速度、加速度、动位移和动应力)均位于同一量级且峰值较为接近。由此可见,本文的数值仿真模型能够从动位移和动应力两个不同的维度模拟重载铁路路基的动力响应,具有良好的可靠性,可用于多工况仿真分析。

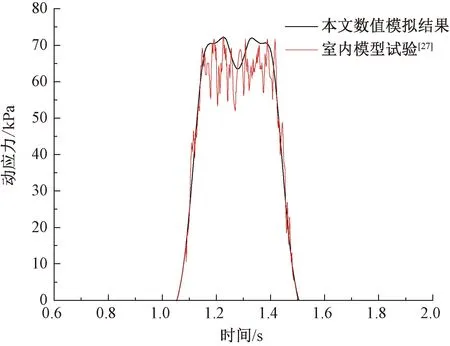
图10 数值模型与室内模型试验的动应力对比分析

3 双线重载路基动力响应分析

3.1 竖向动应力

3.1.1 竖向动应力峰值沿路基面的横向分布

重载铁路路基动应力响应水平是重载铁路设计中需考虑的关键因素之一[28]。图11为6种工况下,路基模型中间断面处(Z=8.4 m)路基面动应力峰值的横向(X向)分布曲线。由图11可知,动应力峰值在轨枕下方呈“马鞍形”分布,均为钢轨下方最大,轨枕中部次之,轨枕端部最小。双向列车与满载列车单向运行时,上行线路基面处的动应力峰值十分接近,而下行线路基面在列车双向运行下的动应力峰值则略高于空载列车单向运行时的数值。

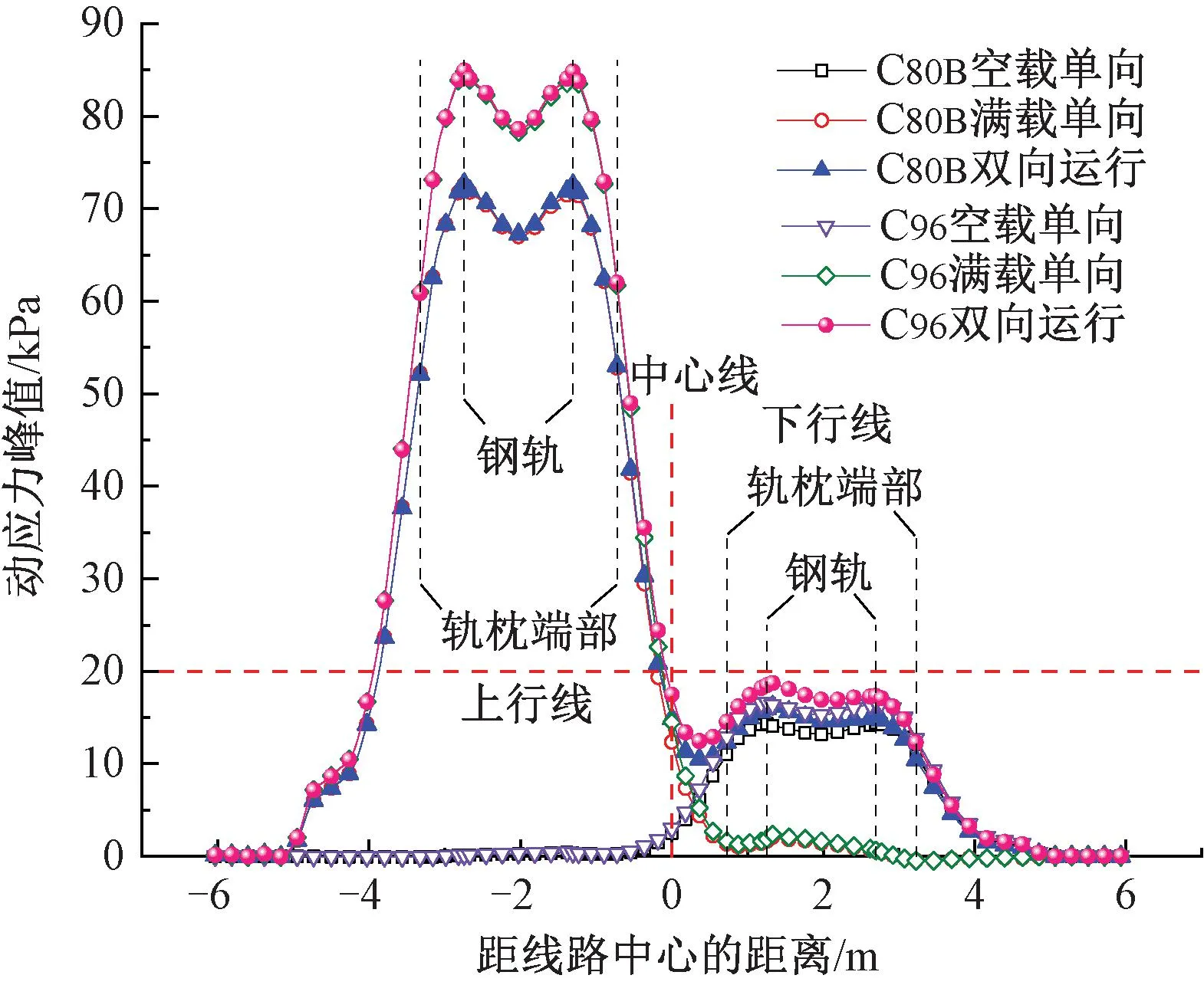
图11 动应力峰值沿路基面的横向分布

列车双向运行下,满载列车轴重由25 t(C80B)增加到30 t(C96)时,5个观测点处的动应力峰值平均增加了16.6%,其中上行线钢轨下动应力峰值最大,由72.1 kPa增加至85 kPa。两种敞车运行下,路基面中心线处的动应力峰值均不足20 kPa,显著小于上行线钢轨下方的动应力水平。此外,满载列车单向通过上行线时,会在下行线侧路基面引起小幅动应力;而空载列车单向通过下行线时,则基本不会在上行线侧路基面引起动应力,说明满载列车的影响范围大于空载列车。

3.1.2 竖向动应力峰值沿路基深度的分布

路基动应力沿深度方向的分布及衰减规律是确定路基基床层厚度的依据[29-30]。图12为C96敞车满载单向运行下,本文数值模拟与Boussinesq公式计算所得P2点处动应力的对比结果。由图12可见,Boussinesq公式计算值略小于数值仿真计算结果。采用Boussinesq公式计算路基动应力时将路基整体近似为单一均匀层,且计算时仅考虑了轮载正下方轨枕荷载的扩散效应,未考虑邻近轨枕荷载于计算点处的叠加效应,这是导致Boussinesq公式计算值偏小的主要原因。图12整体反映出数值仿真结果与Boussinesq公式计算结果量值接近,且路基动应力随深度增加的衰减规律一致,侧面说明了数值仿真结果的合理性。

图12 数值仿真与Boussinesq公式计算所得动应力

图13为6种工况下,测点P2、P3和P4处动应力峰值沿路基深度的分布曲线。P2点处(图13(a))双向列车和满载列车单向运行下,动应力传递至基床层底部(2.5 m)时衰减约71.4%,说明基床层吸收了大部分的振动能量。路基面中心P3点(图13(b))处动应力峰值随深度增加先增大后减小,呈凸形分布,6种工况下P3点处的动应力最大值均位于路基面下0.92 m深度处,其数值约为路基面处动应力峰值的1.47倍。P4点处(图13(c))双向列车与空载列车单向运行下,动应力峰值均随深度的增加而逐渐衰减;满载列车单向运行下的曲线仍为凸形分布,峰值点深度约为2.34 m深度。双向列车运行时,P4点处动应力峰值沿深度的衰减速率较P2和P3点小。

图13 动应力峰值沿路基深度的分布

此外,由图13(a)可知,双向列车与满载列车单向运行下,P2点均位于列车荷载作用区域,动应力随深度的增加逐渐衰减;而空载列车单向运行时,P2点位于列车荷载作用区外,该点处动应力随深度增加呈先增大后减小的规律变化。可见不同线路运行模式下,测点与列车荷载作用区域存在2种不同的空间位置关系,加之列车振动荷载传播路径和扩散效应的影响,致使同一点位处动应力随深度呈现不同的变化规律。另外,图13(c)表明单向列车运行时,空载列车于P4点处引起的动应力在0～1.65 m深度范围内占主导地位,而满载列车引起动应力则在1.65 m深度以下占主导作用。

3.2 竖向动位移

图14为C96敞车运行下,测点P2、P3和P4处的动位移时程曲线,图中负值表示位移方向竖直向下。由图14可知,列车双向运行时的动位移峰值大于单向运行。第一节车厢的前转向架和最后一节车厢的后转向架通过观测点时,动位移时程曲线呈“V”形分布;而前后两节车厢的相邻转向架通过时,曲线近似呈“U”形分布,其原因在于相邻转向架的轮对荷载存在叠加效应,延长了动应力维持高值的时长。

图14 竖向动位移时程曲线(C96敞车)

图15为6种工况下,路基模型中间断面处动位移峰值的横向分布曲线。以C96敞车为例,满载、空载列车单向运行下,动位移最大值分别为2.187、0.408 mm,前者是后者的5.36倍,表明满载列车引起的路基变形远大于空载列车,且满载列车单向运行在下行线钢轨下方路基面引起的动位移最大值是空载列车单向运行时的2.15倍。另外,由图15可知,路基面动位移呈现显著的非均匀分布规律,曲线整体表现为凹形分布,最大值位于轨枕中部位置的下方。如果路基面长期处于不均匀变形状态,长此以往可能会映射至钢轨并引起或加剧轨道的高低不平顺[31]。

图15 动位移峰值沿路基面的横向分布

3.3 竖向速度

图16为3种运行模式下,C96敞车通过时测点P2、P3和P4的竖向速度时程曲线,图16中,正值代表速度方向竖直向上。由图16可知,竖向速度时程曲线呈现明显的周期性,且向上和向下的加速度幅值基本相同。

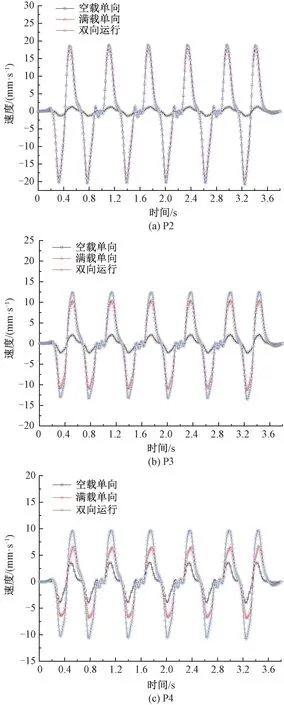
图16 竖向速度时程曲线(C96敞车)

图17为6种工况下路基面速度峰值沿P2、P3和P4点的横向分布图。由图17可知,3个测点在列车双向运行下的速度峰值均高于列车单向运行时的值。各测点处的速度均随轴重的增加而增加,但增加幅度有限,说明轴重对路基面速度响应的影响相对较小。C96敞车工况下,下行线P4点在满载列车单向运行时的速度峰值(6.68 mm/s)明显高于空载列车单向运行时的峰值(3.59 mm/s),前者是后者的1.86倍。

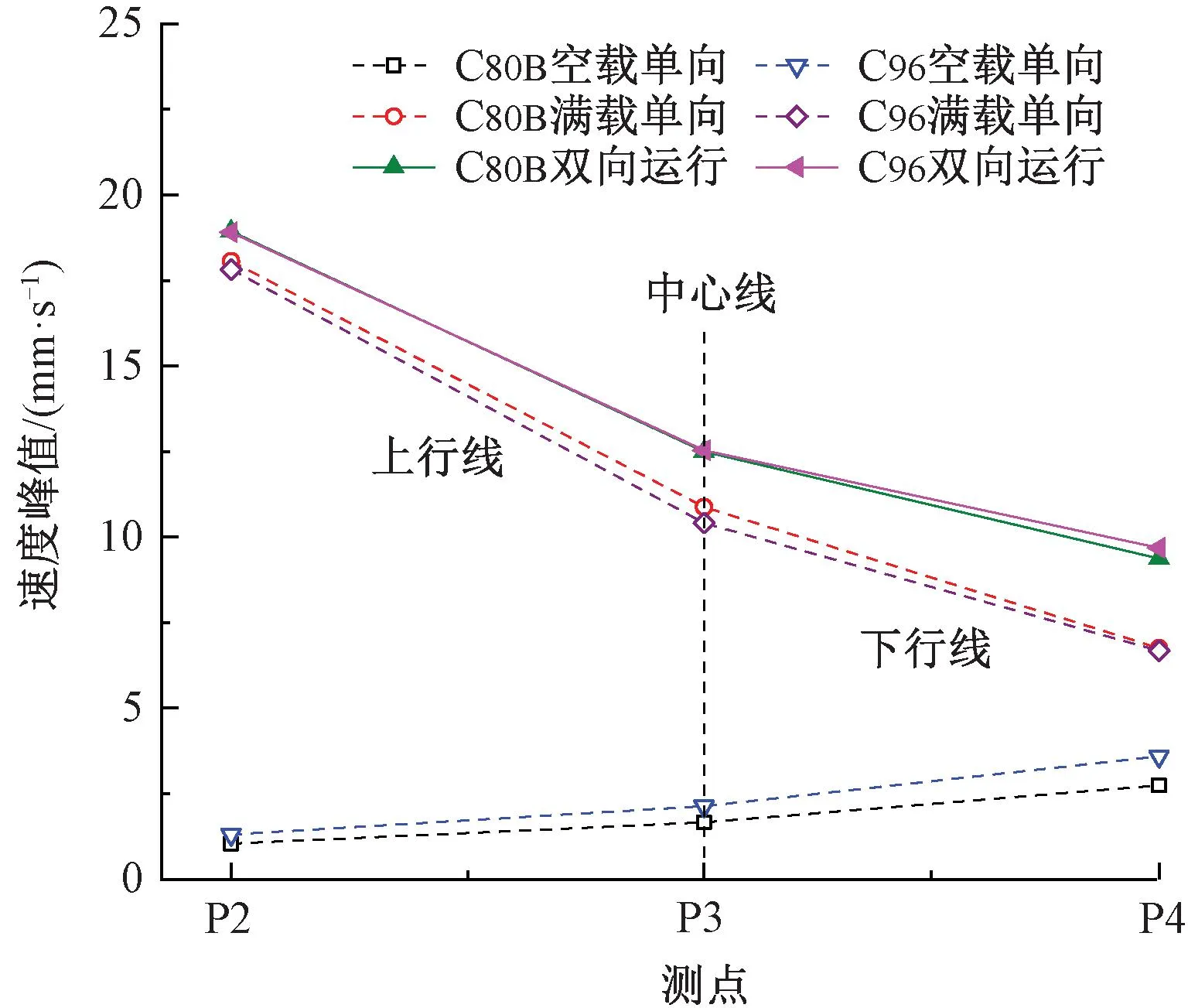
图17 测点处竖向速度峰值

3.4 竖向加速度

C96敞车3种运行模式下P2、P3和P4点的竖向加速度时程曲线如图18所示,图18中正值代表加速度方向竖直向上。竖向加速度时程曲线可以很好地反映相邻转向架的通过情况,且3个观测点在6种工况下的向上加速度略大于向下加速度。

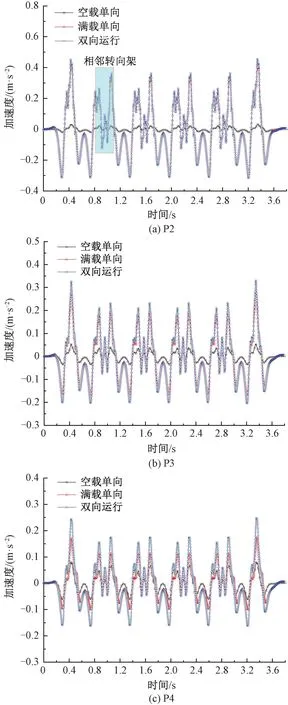
图18 竖向加速度时程曲线(C96敞车)

图19为6种工况下路基面加速度峰值沿P2、P3和P4点的横向分布。由图19可知,C80B敞车运行下,上行线P2点在列车双向运行与满载列车单向运行下的加速度峰值分别为0.408、0.393 m/s2;C96敞车通过时,上述加速度峰值分别提高到0.456、0.426 m/s2,分别增加了11.76%、8.40%。路基面中心P3点在列车双向运行下的加速度峰值是满载列车单向运行的1.2倍,而满载列车单向运行时的加速度峰值是空载列车单向运行时的5.0倍。下行线P4点在空载列车单向运行下的加速度峰值明显低于满载列车单向运行下的峰值,后者为前者的1.97倍。

值得注意的是:由图11可知,满载列车单向运行在下行线路基面引起的动应力低于空载列车单向运行时引起的动应力值;然而,不同于动应力的响应规律,图15、图17和图19反映出满载列车单向运行在下行线路基面引起的动位移、速度和加速度峰值均大于空载列车单向运行于下行线时引起的响应值。此外,双线列车运行时路基的动力响应水平均大于单向列车运行的工况,表明双线列车荷载存在一定的叠加效应。

图20为3种运行模式下,C96敞车通过时测点P2处竖向加速度峰值沿路基深度分布曲线。P2点位于上行线钢轨下方,双向列车和满载列车单向运行下,其所在位置属于列车荷载作用区域,加速度峰值随深度的增加而减小,且衰减速率呈现先快后慢的变化规律。

图20 加速度峰值沿路基深度的分布

4 结论

本文建立了双线重载铁路路基的数值仿真模型,并基于现场实测数据和既有模型试验数据完成验证,系统分析了C80B与C96两种典型敞车在3种不同运行模式下的路基动力响应规律,所得主要结论如下:

1)不同运行模式下,列车于本侧路基面引起的竖向动应力沿横向均呈“马鞍形”分布,即钢轨下方>轨枕中部>轨枕端部。空载列车单向运行时,基本不会在上行线侧路基引起动应力。列车轴重由25 t增加到30 t时,路基面的动应力峰值由72.1 kPa增加至85 kPa。

2)列车通过上行线时,本侧钢轨下方(P2点)处动应力随深度增加逐渐减小,基床层的衰减率超过70%,表明基床层吸收了大部分的振动能量;路基面中心处(P3点)动应力随深度增加先增大后减小;下行线钢轨下方(P4点)双向与单向空载列车运行下的动应力均随深度增加逐渐减小,而满载列车单向运行下则先增大后减小。

3)路基面上,满载列车单向运行引起的动位移峰值可达到空载列车单向运行时的5.36倍。3种运行模式下,路基面动位移呈现明显的非均匀性分布特性,竖向动位移峰值沿路基面横向整体表现为凹形分布。

4)路基面处向上和向下的速度响应幅值基本相同,列车轴重对路基速度响应的影响较小;列车轴重由25 t增至30 t时,本侧线路钢轨下方路基面处加速度峰值增加约10%。

5)双线列车运行时,路基的动力响应水平大于单向列车运行的工况,表明双线列车荷载存在叠加效应;满载列车单向运行于上行线时,下行线钢轨下方路基面处的加速度、速度和动位移峰值均大于空载列车单向运行于下行线的工况,分别可达后者的1.97倍、2.16倍和2.15倍。