悬浮隧道支撑锚索在管体运动状态下的动频率与湿模态
朱 灿, 刘 炎, 易壮鹏
(长沙理工大学 土木工程学院, 长沙 410114)
悬浮隧道是具有显著优势的跨越深、长水道的水下交通结构,近年来受到许多学者的关注[1-2],其中流体环境中的流固耦合机理,交通荷载、地震[3]、爆炸[4]荷载下的结构响应,以及构件、结构力学模型等,是研究的焦点。
张力腿形式是悬浮隧道最常见也是公众最易接受的固定方式,顶底分别与管体、河床连接的锚索是重要支撑构件,对结构稳定和安全起至关重要的作用,因而锚索本身及与隧道管体相互作用的动力行为受到广泛关注。一方面,研究者进行了大量的锚索单独建模研究,如:尾流振子模型[5]、参振模型[6]和Euler梁模型[7],等。研究者还对水流环境中一般悬索进行了多模态[8]和参激振动[9]的非线性建模,克服了不能考虑锚索分布参数、几何非线性和多模态振动的不足。海洋立管[10]、锚链等海洋索的建模技术,以及非流体环境中索的研究成果[11],可为悬浮隧道锚索建模提供借鉴。另一方面,管体运动可导致锚索大幅振动,锚索的参数振动反过来可激发整体振动,锚索单独建模已不能全面反映这种构件之间的动力耦合。于是,研究锚索与管体之间耦合振动的模型应运而生,如:管体等效为阻尼-弹簧-质量块的锚索参振模型[12]、锚索-管体模型[13]。随着研究的深入,锚索及悬浮隧道系统的力学模型越来越精确。
锚索频率、模态的精确获取对识别悬浮隧道振动性能至关重要,而水下锚索的频率与管体运动息息相关。管体运动使得锚索张力不断变化,对应的频率将是一个变值,进而对锚索动力性能产生显著影响,当结构参数组合位于某些特定区间时管体过大的位移会使锚索由张紧进入松弛状态[14]。已有悬浮隧道锚索涡激振动、参激振动及空气中运动边界索[15]的研究大多将锚索频率视为定值,这与实际的吻合程度值得进一步深入探讨。实际上,发生涡激振动时锚索频率的变化极可能导致锁定区间扩大,极限环解将更加复杂;当管体运动频率与锚索固有频率满足一定关系时,将发生参激振动,锚索频率的变化可能激发锚索的大幅振动。然而已有研究对水下索结构频率变化及引起的非线性行为较少涉及,悬浮隧道锚索在管体运动下的频率分布规律值得进一步探讨。此外,锚索湿重沿展向分布存在变化,某些参数分布区间内锚索模态不能假定为谐波函数,进行精确分析需考虑流体环境中锚索的湿模态。已有关于弹性约束充液管道[16]和海洋立管的模态分析表明流体会影响结构的固有频率和模态分布,湿模态分析对处于流体环境的结构振动研究不可缺少。
锚索支撑式悬浮隧道中,管体运动将通过张力变化影响锚索频率,随着管体的运动锚索会出现动频率。基于此,本文将锚索自振特性与结构参数直接关联,提出一种管体运动状态下求解锚索动频率和湿模态的新颖方法。将锚索等效为梁或弦,建立四类力学模型分别探讨管体运动时锚索抗弯刚度、湿重等因素对自振特性的影响。所提动频率概念可为进一步研究构件涡振频率锁定,以及参激、参强联合作用下的复杂非线性行为提供新的处理思路。
1 悬浮隧道管体运动状态下支撑锚索的动力模型与自振特性
1.1 管体运动状态下的锚索动力模型
如图1(a)所示锚索支撑的悬浮隧道,为研究管体运动状态下锚索自振特性,以典型节段管体下方锚索如图1(b)所示为对象建立力学模型。图1中:L为锚索长度;O-xy为以顶端为中心的坐标系;x为轴向;y为横向;θ为水平倾角;f(x,t)为流体作用力,t为时间。为获取管体运动时锚索振动方程,引入假定:①锚索截面材料、几何特性沿长度不变;②锚索顶部与管体的连接等效为具有一定刚度的弹簧;③只考虑x-y平面内的横向振动;④管体、锚索均处于运动状态且锚索张力随时间变化,为获取锚索动频率将整体结构进行拟静态处理且只考虑管体竖向周期振动,锚索即时轴力N(x,t)为[17-18]

图1 悬浮隧道整体布置及锚索模型示意图Fig.1 Schematic diagram of the global layout and cable model of the SFT
N(x,t)=Nt-Waxsinθ+Kacos(Ωt)sinθ
(1)
式中:Nt为锚索顶端张力,Wa=(ρc-ρw)Acg为锚索单位长度湿重;ρc和ρw分别为锚索、流体的密度;Ac为锚索截面积;g为重力加速度;K为管体与锚索之间的连接刚度;α和Ω分别为管体运动幅值和频率。⑤Nt(即式(1)中x,a同时为零的N(x,t)值)由管体振幅为零时锚索索力与该索支撑范围内净浮力相等的原则确定
(2)
式中:At为管体横截面积;d为锚索纵向间距;nc为所截取管体节段锚索的肢数;λ1为管体浮重比。
此外,锚索的截面面积Ac按式(3)取值
(3)
式中:λ2为锚索安全系数;[σ]为锚索容许应力值。管体与锚索之间的连接刚度K取为
(4)
为研究锚索抗弯刚度、湿重等参数对结构自振特性的影响规律,建立如图2所示的M1~M4四类模型。图2中:M1模型同时考虑锚索抗弯刚度和湿重;M2模型忽略湿重;M3模型忽略抗弯刚度;M4模型同时忽略锚索抗弯刚度和湿重。
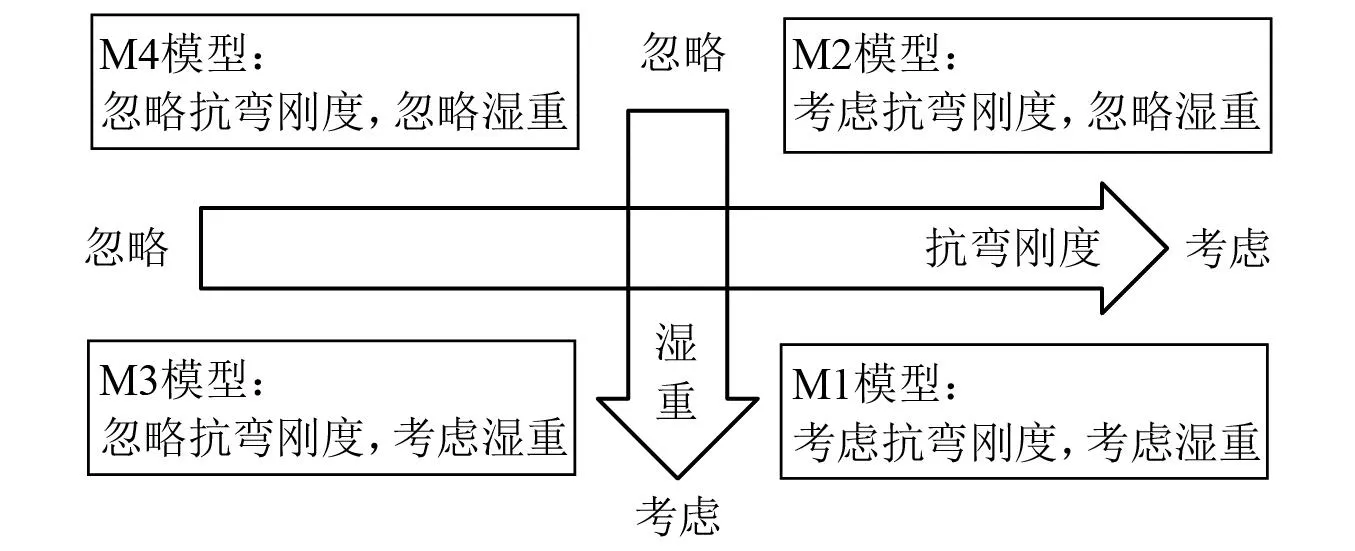
图2 管体运动状态下的锚索模型Fig.2 Cable models under tube motion
在上述四类模型中锚索的顶端静张力、截面积和连接刚度等参数根据悬浮隧道结构的受力特点按照假定⑤依据式(2)~式(4)取值。
1.2 M1模型—考虑锚索抗弯刚度和考虑湿重
在管体运动状态下,根据引入的基本假定,同时考虑抗弯刚度和湿重时锚索的振动方程可写为
(5)

(6)
将位移写为u(x,t)=φ(x)exp(iωt)以分离轴向坐标x和时间t两类变量,其中:ω为振动频率;φ(x)为与ω对应的模态。将其代入与式(5)对应的无阻尼自由振动方程,可以得到
(7)
式(7)的解可以表示为
φ(x)=
A1sinη1x+A2cosη1x+A3sinhη2x+A4coshη2x
(8)
式中,A1~A4为模态系数,且有
(9)
根据两端x=0,x=L的边界条件u(x,t)=0, ∂2u(x,t)/∂t2=0可求得系数A2~A4等于0,且有
η1(x,t)=nπ/L,(n=1,2,3,…)
(10)
式中,频率ω不能写为其他参数的显式,同时与x的分布有关,采用与张杰等研究中类似的处理方法将式(10)在[0,L]内对x积分,可以得到关于ω的超越方程
6η1(L,t)N(L,t)=3nπWa
(11)
式(11)可求解M1模型的锚索固有频率ω,它与锚索的张力分布、自质量、刚度及管体运动状态等相关。由式(8)可知锚索振动模态为φ(x)=A1sinη1x,由于此时η1(x,t)为x函数,锚索湿重使得轴力沿高度分布不一致,将幅值进行修正后的振动模态写为
(12)

1.3 M2模型—忽略锚索湿重
当不考虑锚索湿重时,Wa=0,此时锚索张力沿高度方向为恒定值。振动模态φ(x)可以用式(8)表示。同样, 根据两端边界条件u(x,t)=0, ∂2u(x,t)/∂t2=0可知模态系数A2~A4为0,且振动频率的求解方程可以表示为
η1(0,t)=nπ/L,(n=1,2,3,…)
(13)
此时,锚索的第n阶固有频率ωn可以直接写为
(14)
且振动模态可以写为φ(x)=A1sinη1x,由于此时η1与x无关,模态为标准正弦函数,其中系数A1可由模态规范化条件获取。在忽略湿重的情况下,模态选用正弦函数可简化涡激、参激及参强联合振动等更复杂非线性动力行为的分析,然而忽略湿重将导致频率、模态与实际情况存在误差,后文将讨论这种假设在悬浮隧道支撑锚索中的影响。
1.4 M3模型—忽略锚索抗弯刚度
当支撑锚索忽略抗弯刚度而考虑自身湿重时,对应式(5)和式(7)中与EcIc相关的项消失,此时求解频率和阻尼的常微分方程可以写为
(15)
式(15)为弦的一般求解方程,其解可以表位为
φ(x)=A1sinη3x+A2cosη3x
(16)
式中,A1和A2为模态系数,且
(17)
根据两端x=0,x=L的弦边界条件可求得系数A2等于0,且有
η3(x,t)=nπ/L,(n=1,2,3,…)
(18)
由于考虑了湿重沿锚索长度方向的分布,式(18)中ω与x的分布有关,同样将式(18)在[0,L]内对x积分,可以得到第n阶固有频率ωn的表达式
(19)
为考虑湿重的索导致的轴力沿高度方向分布不一致,将锚索振动模态的幅值进行修正并写为

(20)
式中,系数A1由模态规范化获取。
1.5 M4模型—同时忽略锚索抗弯刚度和湿重
当支撑锚索忽略抗弯刚度且不考虑自身湿重时,由式(11)~式(14)并取Wa=0可将频率写为
(21)
且振动模态可以写为φ(x)=A1sin[η3(0,t)x],同样η3(0,t)与x无关,模态为标准正弦函数。
2 算例分析
作为一种新型的水下交通结构,通过参数分析获取管体运动状态下锚索与各种悬浮隧道结构参数的对应关系从研究角度来说是可行的。本文参阅已有悬浮隧道的研究,选取基本参数如下:管体横截面积At=165.13 m2,流体与锚索的密度分别为ρw=1 000 kg·m-3和ρc=7 850 kg·m-3,附加质量系数Cm=1.0,锚索弹性模量Ec=210 GPa,锚索容许应力[σ]=1 350 MPa,锚索安全系数λ2=4,肢数nc=2, 纵向间距d=100 m, 管体运动频率Ω=2 rad·s-1。管体的浮重比λ1、运动幅值为a以及锚索的水平倾角θ、竖向高度h为重要的影响参数,研究其在一定范围内变化时各锚索模型所得动频率与湿模态的分布规律。此外,锚索轴向力Nt、截面积Ac、惯性矩Ic、长度L及与管体的连接刚度K可由式(2)~(6)根据相应的关系确定。
2.1 管体运动状态下锚索的动频率与湿模态
图3给出了悬浮隧道支撑锚索在管体运动状态下基于M1~M4模型的频率图,其中λ1=1.35,a=0.05 m,θ=60,h=100 m。对于悬浮隧道结构体系而言,管体在竖向周期运动acos(Ωt)的状态下锚索与管体之间通过作用力N(x,t)和连接刚度K相互作用,基于M1~M4模型得到的锚索频率随时间的推移呈现周期性变化。为与已有固有频率概念不随时间变化相区别,本文称随管体运动而发生变化的锚索频率为“动频率”,典型的锚索各阶动频率如图3(a)所示。更进一步,将基于静力平衡时锚索索力与支撑范围内净浮力相等原则得到的几何、材料参数分别代入可写为显式的M2~M4模型的频率公式(即式(14)、式(19)、式(21)),可得
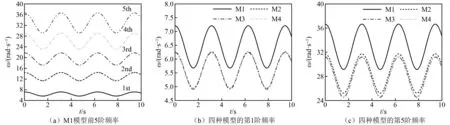
图3 管体运动状态下的锚索动频率Fig.3 Dynamic frequencies of cable under tube motion

(22)
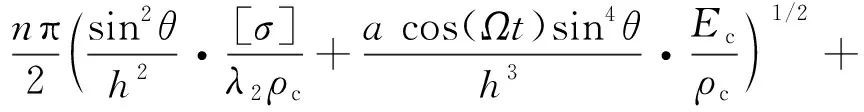
(23)
(24)
由式(22)~式(24)可知,锚索动频率的变化周期为2π/Ω,且极大值、极小值与cos(Ωt)=±1对应。此外,由图3(a)和式(22)~式(24)可知,动频率极大值与极小值之间的变化幅度随着频率阶次的升高而变大。通过基于M1~M4四种模型所得典型频率(见图3(b)中的第1阶和图3(c)中的第5阶)的比较,M1模型所得频率明显大于其他三种模型所得频率,基于M3模型与M4模型所得频率非常接近。这些说明锚索的抗弯刚度、湿重及其他结构参数对不同阶次的频率有着不同程度的影响,后文将分析M1~M4模型所得频率与浮重比、锚索倾角、竖向高度、管体运动幅值之间的变化规律和参数敏感程度。
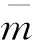
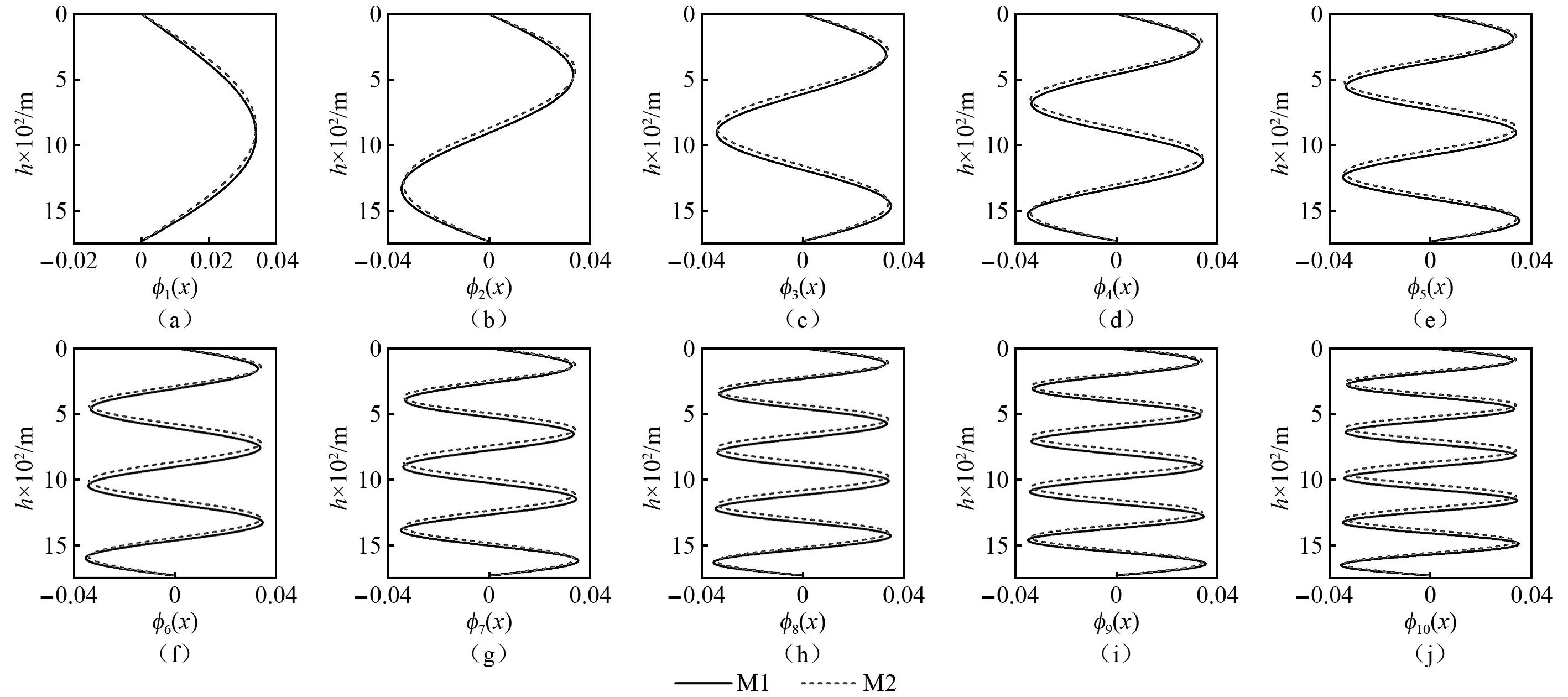
图4 锚索的规范化模态示意图Fig.4 Diagram of normalized modes for cables
2.2 锚索随浮重比变化的振动频率
锚索频率在管体运动状态下随着时间变化在极大值与极小值之间变化,为了描述其幅度与各类结构参数之间的变化规律引入“频率带”的概念,即某一组特定参数下频率带的上、下限值分别取动频率的极大、极小值。图5给出了基于四种模型所得锚索频率随浮重比λ1变化的规律图(a=0.05 m,θ=60,h=50 m),其中四个子图对应阴影部分所标识的区域分别为基于M1~M4所得第2阶动频率的频率带,其余阶次的频率带只标注了上、下限,中间部分为频率带范围。此外,每阶频率带的范围与频率阶次密切相关,由式(23)和式(24)及图5(c)、图5(d)的计算结果可知M3、M4模型所得各阶动频率带宽与频率阶次n成正比,例如M4模型中构成频率带宽的上限ωnt、下限ωnb可写为

图5 锚索“频率带”随浮重比变化的分布图Fig.5 Diagram of “frequency band” for cable versus buoyancy weight ratio
(25)
而由式(11)、式(14)(或式(22))及图5(a)、图5(b)的计算结果可知由于锚索抗弯刚度的存在M1、M2模型所得各阶频率带宽度与频率阶次n接近于成正比。
由图5可知,在浮重比λ1由1.01增至1.50的过程中,基于M1、M2模型所得低阶次频率变化不明显而高阶次频率增加明显;基于M3、M4模型所得各阶频率均不随λ1的变化而变化,其原因在于两种模型的频率表达式(23)和式(24)中与λ1相关的项已经消去。更进一步,图6给出了基于不同模型所得的各阶次频率:对比M1模型和M2模型所得各阶频率可知,在考虑抗弯刚度的情况下湿重对频率的影响很大,不可忽略;对比M3模型和M4模型发现,在不考虑抗弯刚度的情况下湿重对频率的影响很小,几乎可忽略。此外,对比M1模型和M3模型所得各阶频率可看出,在考虑湿重的情况下抗弯刚度对频率的影响很大,在λ1变化范围内均不可忽略;对比M2模型和M4模型可得,在不考虑湿重的情况下抗弯刚度对频率的影响较小,在λ1取小值时可忽略而λ1取大值时不可忽略。
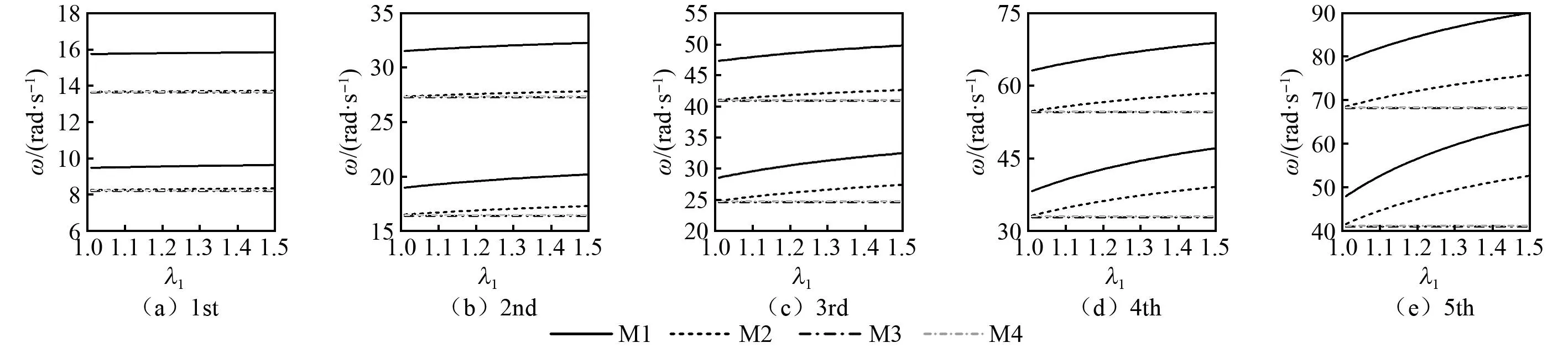
图6 锚索各阶动频率随浮重比变化的对比图Fig.6 Comparison diagram of each-order dynamic frequency for cable versus buoyancy weight ratio
2.3 锚索随倾角变化的振动频率
图7给出了基于四种锚索模型所得频率带随水平倾角θ变化的分布规律(λ1=1.35,a=0.05 m,h=50 m),同样阴影部分区域标识第2阶动频率的频率带,其余阶次的频率带只标注上、下限。由图7可知,各阶频率带的带宽均随着θ的增大而变宽,当锚索竖直(θ=90)时频率带的带宽达到极值。在θ增大的过程中,基于M1模型得到的频率带下限单调递减,对应的上限则先减后增;基于M2~M4模型得到的频率带上限和下限均单调递增,最终稳定于某一值附近。基于M1模型所得频率带与其余三种模型的最大差异区间位于θ取较小值时,此时由同时考虑锚索抗弯刚度和湿重影响得到的频率值显著大于忽略其中一种或两种因素得到的频率值。

图7 锚索“频率带”随水平倾角变化的分布图Fig.7 Diagram of “frequency band” for cable versus horizontal inclined angle
图8给出了由M1~M4得到的随水平倾角θ变化的各阶次频率,通过不同模型所得频率之间的对比可知锚索抗弯刚度与湿重对频率的影响存在与图6类似的规律。在考虑抗弯刚度的情况下湿重对频率的影响很大,不可忽略;在不考虑抗弯刚度的情况下湿重对频率的影响很小,几乎可忽略。在考虑湿重的情况下抗弯刚度对频率的影响很大,在θ变化范围内对应频率带分布差异明显;在不考虑湿重的情况下抗弯刚度对频率存在一定的影响,在θ取小时可忽略而λ1较大时不可忽略。

图8 锚索各阶动频率随水平倾角变化的对比图Fig.8 Comparison diagram of each-order dynamic frequency for cable versus horizontal inclined angle
2.4 锚索随竖向高度变化的振动频率
图9给出了基于M1~M4模型所得频率带随锚索竖向高度h的变化规律(λ1=1.35,a=0.08 m,θ=60)。由图9可知,以阴影部分区域(第2阶)为代表的典型动频率带随h变化的分布特征呈现与其他参数不同的规律。整体上,基于四类模型所得各阶动频率的带宽均随h的增大而变窄。当h增至某一值时,由M3、M4模型所得各阶动频率带宽与频率阶次n成正比,由M1、M2模型所得各阶动频率带宽与频率阶次n接近于成正比。在h增大的过程中:M1~M4模型对应的频率带上限均单调递减且在h较小时减幅非常显著;下限在h大于某特定值时先增后减,在h小于该值时锚索出现松弛且分布特性因模型各异。
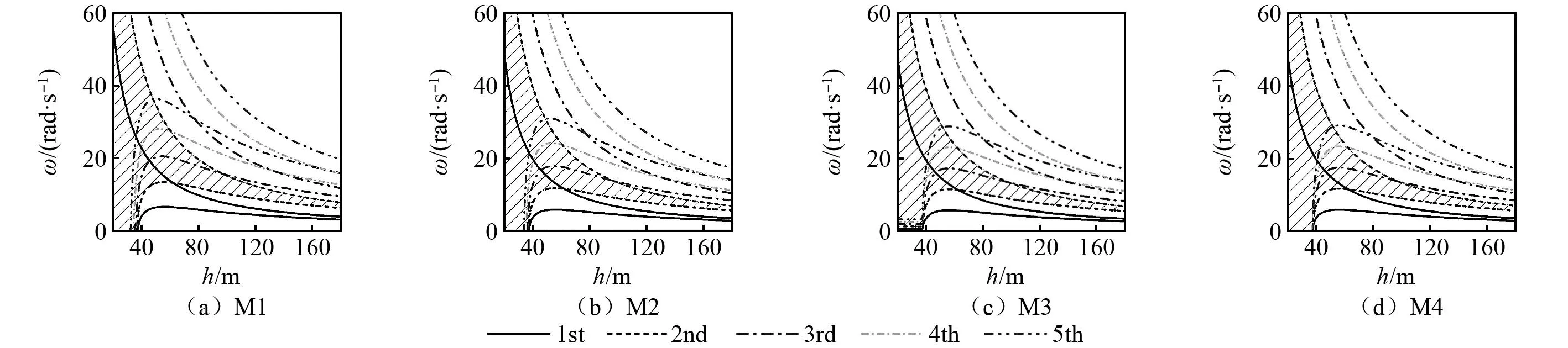
图9 锚索“频率带”随竖向高度变化的分布图Fig.9 Diagram of “frequency band” for cable versus vertical height
对于M1、M2模型,在h变化过程中下限与水平轴相交于hst,此交点为张紧与松弛两种状态的分界点,hst的取值与几何、材料参数及模态阶次有关,其中,M2模型对应的hst可由令式(22)右边大括号内的项等于零且cos(Ωt)=-1所得关于hst的方程求得。对于M3模型,由式(23)右边两个大括号内的项等于零且cos(Ωt)=-1可分别得到两个交点hst1 图10给出了基于M1~M4模型的各阶次频率随h变化的分布图,通过不同模型之间的对比可知锚索抗弯刚度、湿重对频率的影响存在与图6、图8类似的规律。对比M1模型和M2模型,在考虑抗弯刚度的情况下湿重对频率的影响很大;对比M3模型和M4模型,在不考虑抗弯刚度的情况下湿重对频率的影响很小,几乎可忽略;对比M1模型和M3模型,在考虑湿重时抗弯刚度对频率的影响很大,二者差异在h变化区间内均不可忽略;对比M2模型和M4模型,在不考虑湿重的情况下抗弯刚度对频率的影响较小,在h增至一定值时可忽略。 图10 锚索各阶动频率随竖向高度变化的对比图Fig.10 Comparison diagram of each-order dynamic frequency for cable versus vertical height 图11给出了由M1~M4模型所得频率带随管体运动幅值a变化的分布规律(λ1=1.35,θ=60,h=50 m),以阴影部分区域(第2阶)为代表的典型动频率带随运动幅值变化的分布特征显示四类模型的动频率分布特征除了a增至一定程度时的下限值外整体上分布类似。基于四类模型的各阶动频率带宽均随a的增大而变宽,由于上、下限与cos(Ωt)=±1对应,通过式(22)~式(24)和图11可知当a小于某一值时,由M3、M4模型所得各阶动频率带宽与频率阶次n成正比,由M1、M2模型所得各阶动频率带宽与频率阶次n接近于成正比。在a增大的过程中,四类模型对应的频率带上限均单调递增。 图11 锚索“频率带”随管体运动幅度变化的分布图Fig.11 Diagram of “frequency band” for cable versus amplitude of tube motion 值得注意的是,频率带下限在a小于某特定值时单调递减,而a大于该值时锚索出现松弛且分布特性因模型各异。在a变化过程中,M1模型(见图11(a))和M2模型(见图11(b))的频率带下限与水平轴相交于锚索张紧与松弛状态的分界点ast,其中,令式(22)右边大括号内的项等于零且cos(Ωt)=-1可得M2模型对应的ast,它可表述为几何、材料参数及抗弯刚度、模态阶次等的函数。对于M3模型,此时令式(23)右边两个大括号内的项等于零且cos(Ωt)=-1可分别得到两个交点ast1>ast2,实际下限不会达到零,下限值由ast2代入式(23)得到且在a>ast2时不再变化,图11(c)中频率带下限分布与此吻合。对于M4模型,令式(24)中右边大括号内的项等于零且cos(Ωt)=-1可得下限与水平轴的交点ast=hcos2θ·[σ]/(λ2Ec),可知它为一个与抗弯刚度、模态阶次无关的数,因而正如图11(d)所证实的不同阶次频率对应的ast汇聚在一起。 基于M1~M4模型的各阶次频率随a变化的分布规律如图12所示,通过不同模型之间的对比分析抗弯刚度、湿重对频率带的影响。与图6、图8、图10中结构参数的影响规律类似,通过相关模型所得频率带之间差异的类比可知:在考虑抗弯刚度的情况下湿重对频率的影响很大;在不考虑抗弯刚度时湿重对频率的影响很小几乎不可忽略;考虑湿重时抗弯刚度对频率的影响很大,二者频率带的差异在管体运动时不可忽略;不考虑湿重时抗弯刚度对低阶频率的影响很小而高阶频率中不可忽略。 以悬浮隧道支撑锚索为研究对象,根据考虑构件抗弯刚度、湿重的方式建立了M1~M4四类力学模型,研究了管体运动状态下锚索的自振特性,及与浮重比、锚索倾角、竖向高度和管体运动幅值之间的关系,主要结论如下: (1)在悬浮隧道结构拟静态处理,锚索顶端张力与支撑范围内净浮力相等的前提下,锚索在管体运动状态下出现随着时间变化的周期性“动频率”,随系统参数变化的“频率带”与浮重比、倾角、竖向高度和运动幅值均相关。 (2)锚索湿重、竖向高度是影响湿模态的两个主要因素。h≤500 m时基于四类模型所得湿模态非常接近;h>500 m时存在一定的差异。h较大的情况下,考虑锚索湿重时模态振幅在深度方向逐渐增加,不考虑锚索湿重时振幅在深度方向不变。 (3)考虑抗弯刚度时动频率随浮重比的变化而改变,各阶频率带宽与阶次接近于成正比;不考虑抗弯刚度时动频率上、下限及频率带宽均不随浮重比发生变化,各阶频率带宽与阶次成正比。 (4)在锚索水平倾角增大的过程中,各阶动频率带的带宽增大;基于M1模型得到的频率带下限单调递减,对应上限先减后增;基于M2~M4模型得到的频率带上、下限均单调递增。 (5)在锚索竖向高度h增大的过程中,各阶动频率带的带宽变窄,上限单调递减且在h较小时减幅非常显著;下限在h (6)各阶动频率带的带宽随着管体运动幅值的增大而增大,考虑抗弯刚度时频率带宽与阶次接近于成正比,不考虑抗弯刚度时频率带宽与阶次成正比。频率带的上、下限与cos(Ωt)=±1对应,其中下限在a>ast(即张紧与松弛的分界点)时锚索出现松弛且分布特性因模型各异,且ast与几何、材料参数及抗弯刚度、模态阶次存在对应关系。 (7)考虑抗弯刚度时湿重对频率的影响很大,不可忽略;不考虑抗弯刚度时湿重对频率的影响很小,几乎可忽略;考虑湿重时抗弯刚度对频率的影响很大,在各种参数变化范围内均不可忽略;不考虑湿重时抗弯刚度对低阶频率的影响很小而高阶频率中不可忽略。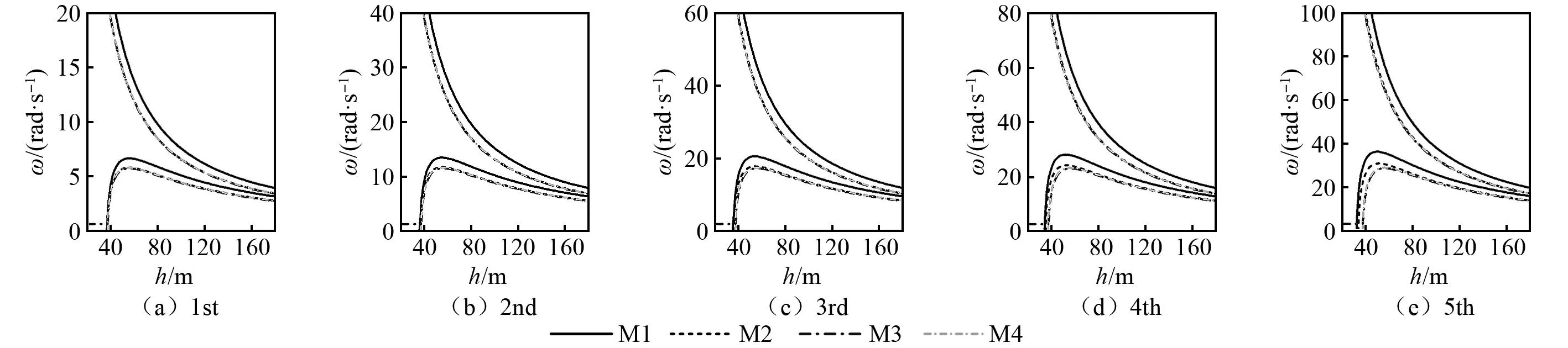
2.5 锚索随管体运动幅值变化的振动频率

3 结 论

