基于有约束L1/2范数稀疏正则化的声源识别方法
潘 薇, 李远文, 冯道方, 黎 敏
(1.北京科技大学 钢铁共性技术协同创新中心,北京 100083; 2.北京科技大学 流体与材料相互作用教育部重点实验室,北京 100083; 3.北京科技大学 机械工程学院,北京 100083)
噪声水平是飞机舱内声学设计的一个重要指标,高强噪声不仅会影响飞行器结构的安全性和机载设备的稳定性,还会影响乘客的舒适度。舱内离散性噪声源具有稀疏分布的特性[1-4],通过识别舱内离散噪声源,实现噪声源高精度定位和声源幅值的准确重构,可以掌握声场的辐射特性,进而可以降低舱内噪声水平,实现噪声有效控制。
近场声全息方法通过记录被测声源表面附近的声压或质点振速,运用空间声场变换算法即可实现声场可视化,从而使得噪声源的识别结果更加直观、可靠。Koopmann等[5]首次提出了基于等效源法的近场声全息技术,该方法可适用于任意形状及尺寸的声源测量,且对声场建模所需的自由度少,计算精度与效率较高,因而得到了广泛的应用。由于传声器的数量有限,导致等效源和测量面之间的传递矩阵总是欠定的。为了处理求解等效源强的这个病态问题,需要引入正则化方法来抑制和滤除奇异值较小的项,防止测量误差在重构过程中被过度放大。传统正则化方法通常可分为L2正则化和L1正则化两类。
在L2正则化方面,大多采用Tikhonov[6]正则化方法来稳定等效源振幅的求解过程。为了进一步提高声源识别的分辨率和适用性,有学者将正则化方式进行了优化。Pereira等[7-8]提出了一种改进的迭代加权(iterative weighted equivalent source method,IWESM)算法,通过引入迭代加权矩阵,大大提升了传统ESM方法的空间分辨率,但该方法并不适用于中高频声源的识别。向宇等[9]利用具有较强指向性的射线波函数来替换传统的单层势或双层势波函数,获得了更精确、更稳定的声源识别结果,但如何优选射线波函数是该方法的难点问题。除了对正则化方式进行改进以外,有学者通过优化正则化参数来得到理想的声源识别性能。Tan等[10]提出了一种增强抗干扰能力的正则化参数确定方法,该方法在低信噪比的情况下鲁棒性较好,但该方法对小奇异值产生了过度惩罚,所以并不适用于高信噪比环境下的远距离测量。Zhang等[11]采用经典黄金分割法搜索正则化参数,一定程度上提高了等效源强求解的稳定性。上述优化方法有效改善了传统ESM的空间分辨率和抗噪性能,但是仍然无法避免声源重构幅值偏低问题。这是由于传统L2范数正则化方法是基于具有伪逆的经典最小二乘原理来求解的,该原理假设模型空间分布连续光滑,正则化方法选出的具有最小范数的解将倾向于将源强能量分散到所有等效源中,容易造成能量耗散,导致声源识别幅值偏低。另外,声全息技术仍然受限于奈奎斯特采样定理,这对上限分析频率的设置带来了影响。因此,在宽频带内寻求重建性能更优的声全息方法具有重要意义。
针对传统基于L2范数正则化等效源方法存在的问题,受到压缩感知(compressive sensing, CS)理论[12-13]的启发,对于空间稀疏分布声源,可以将高维度特征矢量进行降维,通过添加L1范数惩罚来获取等效源强的稀疏解。这种思想突破了奈奎斯特采样定理的频率上限,提高了声源识别方法的位置识别分辨力和强度估计准确度,使得NAH的性能得到了大幅度的提升。Chardon等[14]首次将稀疏正则化应用在基于空间离散傅里叶变换的NAH过程中,而Fernandez-Grande等[15]则首次将压缩感知与等效源法相结合,获得了优于Tikhonov正则化的声源识别结果。为了进一步增强信号的稀疏性,有学者在压缩感知理论基础上,寻求更优的稀疏正交字典。Koyama等[16]基于CS理论找到表示空间近场稀疏特征的基函数,提出一种在空间奈奎斯特极限以上重构声信号的方法,但是该方法仅适用于近场小尺寸声源测量,且目前仅适用于线性阵列测试。Hu等[17]采用奇异值分解(singular value decomposition,SVD)来获得声场的一系列正交基,Bi等[18]针对空间稀疏或扩展源设计了稀疏正则化过程中的三个稀疏基。在合适的基字典中,可以获取具有稀疏或接近稀疏表示的信号,大大降低了采样成本[19]。除此之外,有的学者基于稀疏正则化原理,在求解全局最小值的算法方面进行了优化改进。Hald[20]提出采用最速下降法求解等效源强,即宽带声全息(wideband holography, WBH)方法,通过在中间迭代过程强制滤波,有利于去除虚假声源。虽然WBH方法拓宽了声全息能够识别的声源上限频率,但对于中低频声源的识别能力有限。为此,Xu等[21]在其基础上,提出了基于两步迭代收缩阈值算法(monotonic two-step iterative shrinkage/thresholding,MTwIST),在识别相对较低频率的相干源时,重建精度和分辨率表现得更好。但是,上述方法均是基于L1范数进行的,无法进一步加强解的稀疏性,零值元素不能完全压缩为0,进而产生额外偏置[22-23],也就不能以最少的测量值实现信号的高精度恢复[24]。因此,需要在等效源强求解过程中引入更合适的正则化项,以获取更好的声源识别结果。
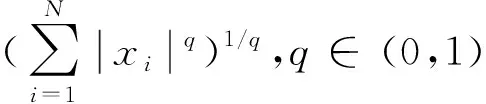
为了解决上述问题,本文提出了一种基于有约束L1/2范数稀疏正则化的声源识别方法。首先,建立等效声源与全息面之间的声场传播模型,基于Tikhonov正则化方法得到等效源强的解范数,作为后续L1/2正则化的解范数约束条件;然后,构造有约束L1/2正则化目标函数,基于CVX工具包求解得到等效源强;最后,在估计等效源强和权值之间进行交替更新,在算法迭代计数达到指定的最大迭代次数时终止,得到声场分布云图,实现声源识别。新方法的优势在于:一方面,通过迭代求解过程,将对声场拟合无意义的等效源项的权重置为零,进一步增强了解的稀疏性,且可以有效避免额外偏置,能够从高维特征中提取并凸显主要有效信息,声源识别精度更高;另一方面,通过设置解范数的约束条件,将关于等效源能量分布的声场先验知识引入正则化过程,有效避免了过度拟合的发生,使得模型的泛化能力更强,计算结果更稳健。
本文基于质点振速传感器采集得到声场辐射振速矢量,研究基于有约束L1/2范数稀疏正则化的声源识别方法,实现空间分布声源的准确定位与幅值量化。开展了数值模拟与普通室内环境中的双声源识别实测实验,证明了方法的有效性。
1 方法理论
1.1 等效源法的基本原理
ESM的基本原理是将实际声场用一系列等效源辐射的声场之和来代替,而等效源通常被布置于声源内部或测量表面附近。假设等效源面上分布N个等效源,测量面上设置M个测点,测量面上M个测点处的质点振速可看作N个等效源辐射质点振速的叠加。
将测量质点振速vh,等效源强度q与格林函数Gv之间的声学响应传递关系写成矩阵形式
vh=Gvq
(1)
式中:vh为测量质点振速列向量(M×1);q为等效源强构成的列向量(N×1);Gv为等效源与测量面之间的质点振速传播格林函数(M×N),表达式如式(2)所示
(2)
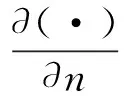
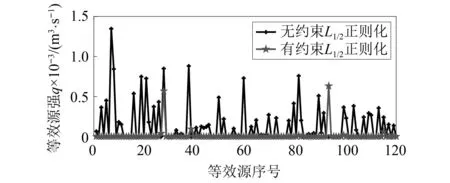
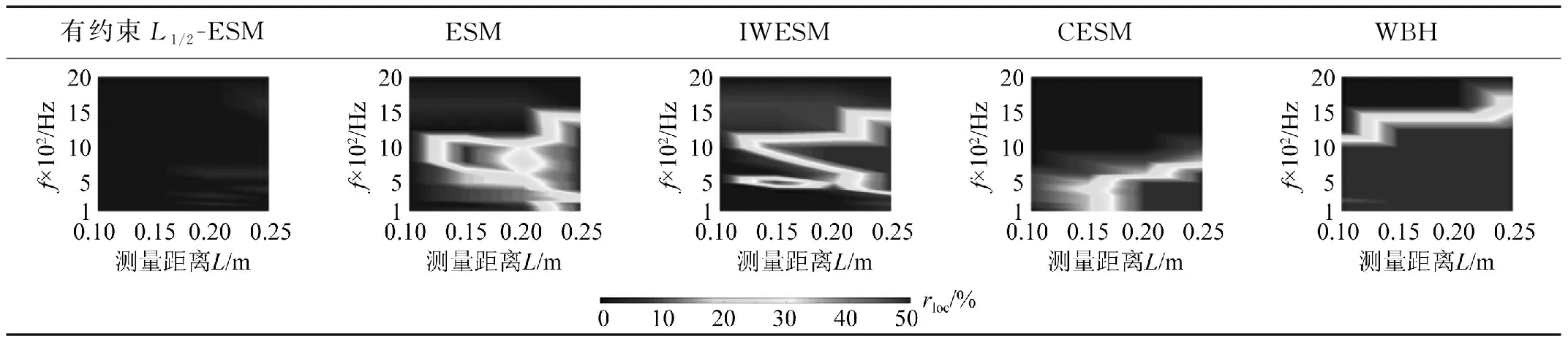
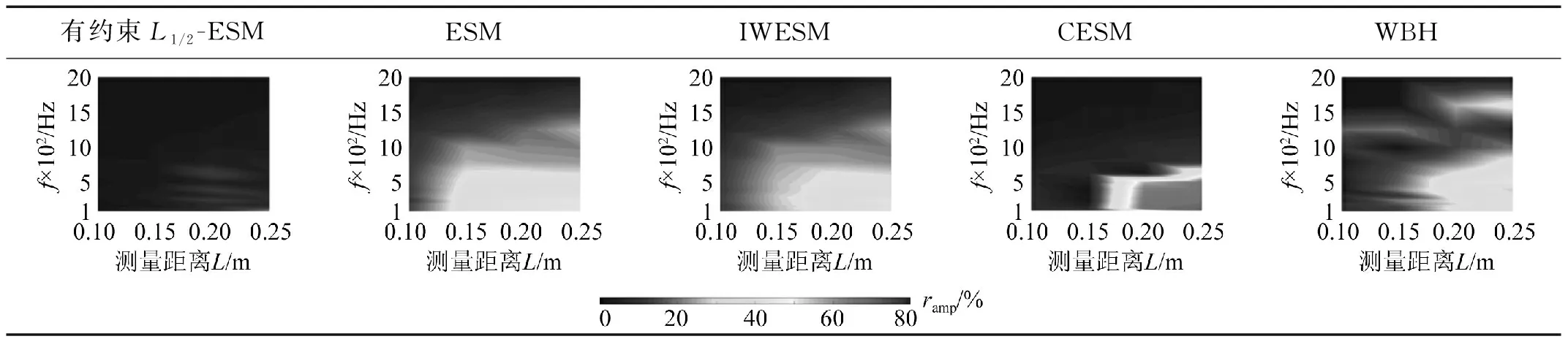
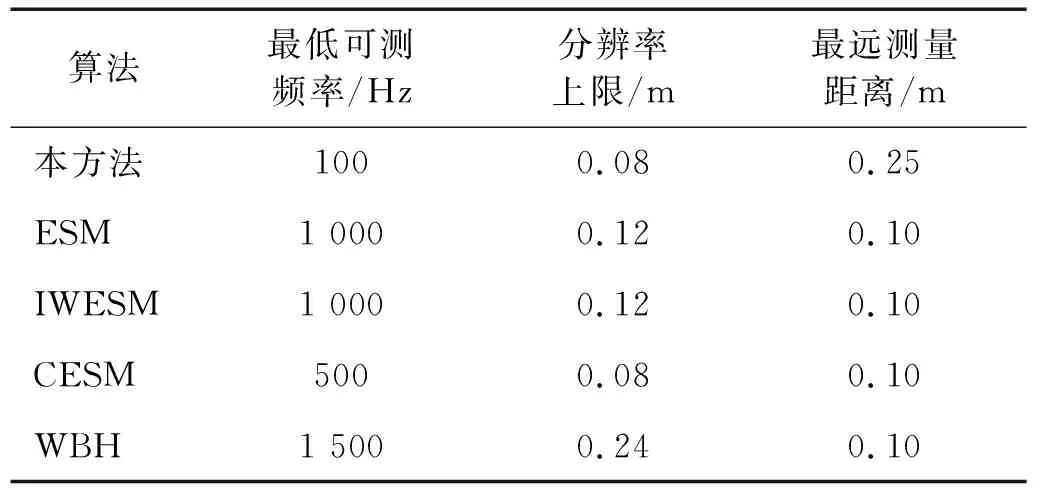
将式(2)代入式(1)中,求解出等效源强向量q,可以实现声源的识别。但是,受限于测试条件和测量成本,测点数目往往少于等效源数目,即M 本文在求解等效源强的过程中引入L1/2范数正则化,其求解公式如式(3)所示 (3) (4) 本文通过施加解范数约束条件,限制数据误差的无限放大,避免了拟合模型盲目寻求小的经验误差,而导致模型对于新样本泛化性差的问题。式(3)本质即为在解范数约束条件下,寻求目标函数最小化对应的q。 根据范数的定义,可以将式(3)改写为 (5) 定义W=q-1/2,那么式(5)可以进一步改写为 (6) 通过式(6),将非凸优化L1/2正则化问题转化为了加权最小二乘优化问题。进一步,通过对惩罚项进行迭代加权处理,逐步动态调整源强分量对损失函数的贡献率,可以限制源强解空间的大小,使得较大权重的等效源强峰值更加突出。 对于第l次迭代,式(6)可改写为 (7) (8) 更新迭代次数l=l+1,当迭代计数l达到指定的最大迭代次数lmax时,终止迭代,否则,转到式(7),重复上述步骤,直到达到最大迭代次数。 方法流程图如图1所示。 图1 基于有约束L1/2范数稀疏正则化的声源识别方法流程图Fig.1 Flow chart of sound source identification method based on constrained L1/2 norm sparse regularization 步骤1在声源附近布置一个测量平面,采集声源辐射的质点振速时域信号,进行傅里叶变换得到每个测量点处的质点振速频域信号vh; 步骤2在声源面附近布置N个等效声源,建立测量面测点处的质点振速信号vh与多个等效源强q之间的传递关系; 步骤3基于Tikhonov正则化求解得到源强的解范数值norm(q,1),作为后续的约束条件; 步骤4设置最大迭代步数,初始迭代次数,以及N个等效源强的初始权重,利用式(7)进行循环迭代; 步骤5通过CVX工具箱求解式(7),得到等效源强解后,更新权重矩阵W(l),直到达到最大迭代次数,输出此时的源强qlmax作为最终的等效源强向量q; 步骤6得到等效源强向量q后,通过建立重构面的质点振速vs与等效源强q之间的传递关系vs=Gvsq,可以实现声源识别。其中,Gvs为等效源与重构面之间的质点振速传播格林函数。 在仿真计算过程中,设置两个单极子脉动球源,同时产生单频信号,球半径0.04 m,表面振速0.03 m/s。布置平面均匀网格传感器阵列,共11×11个测点,测点之间间隔0.04 m。以测量面的中心位置为坐标原点,水平方向为x轴,竖直方向为y轴,垂直于测量面的法向方向为z轴,建立坐标系,双声源和测量面的几何位置如图2所示。重构面与测量面的大小相同,被划分为一系列离散的聚焦点,相邻聚焦点之间的间距均为0.02 m。 图2 数值模拟试验几何位置示意图Fig.2 Geometric position diagram of numerical simulation experiments 图2中:R为双声源间隔;L为传声器到声源表面之间的测量距离;LR为重构面到声源表面之间的重构距离。将等效源布置在声源所在平面上,间隔与测量点间隔相同。为了定量评价方法的准确性,提出以下评价指标。 定义声源定位相对误差 (9) 式中:R为双声源间距;(xA,yA)为声源A位置;(xA0,yA0)为实际声源A的位置;(xB,yB)为声源B的位置;(xB0,yB0)为实际声源B的位置;声源定位相对误差errorloc为两个声源定位误差errorlocA和errorlocB的均值。 定义质点振速幅值重构相对误差 (10) 式中:vtA为声源A处的幅值真值;vrA为重构声源A处的幅值;vtB为声源B处的幅值真值;vrB为重构声源B处的幅值;质点振速幅值重构误差erroramp为双声源幅值误差的均值。 根据声源频率f、测量距离L、双声源间距R、信噪比RSN的不同,设置了如下的仿真试验,如表1所示,以探究声源识别方法的声源定位与幅值重构的准确性,分析算法的分辨率性能。 表1 仿真试验设计Tab.1 Design of simulation experiments 试验设计有两点说明:①考虑到在测量过程中,难以直接测得声源表面的幅值,因此以0.05 m处的测量值为真值,并分别利用式(9)和式(10)来评价声源定位和幅值重构的准确性;②在仿真验证阶段,通常将一定信噪比[39-41]的时域噪声添加到目标信号中。本文采用频域加噪的方式,原因在于,在相同信噪比的情况下,时域加噪是将噪声的能量分散在频谱的各个频点上,而频域加噪是将噪声能量全部集中在单一频点上,此时噪声对于目标信号的干扰作用更强烈,更能够反映出实际测试工况。在本文中,实测情况与仿真环境下添加30 dB信噪比频域噪声较为接近,因此,本文在仿真计算部分,在频域添加信噪比30 dB的高斯随机噪声,约相当于时域添加信噪比-15 dB噪声。 以L=0.10m/R=0.24 m//f=1 000 Hz/LR=0.05 m时的声源识别问题为例,说明对L1/2稀疏正则化添加约束的必要性,对于其他工况得到的结论相同,此处不再赘述。分别在图3中给出有/无约束条件下的L1/2正则化方法得到的声源识别结果与真值结果。其中,理论真值是通过脉动球源的声场辐射理论公式直接计算得到的。 图3 基于有/无约束L1/2正则化与理论声源识别结果对比Fig.3 Comparison between theoretical values and sound source recognition results based on constrained / unconstrained L1/2 regularization in the simulation part 为了更清晰地显示不同方法重构幅值与理论值之间的接近程度,本文将同一工况下的不同方法输出值与理论真值全部按照统一的色阶进行展示。设置颜色栏的下限为所有重构幅值与理论幅值之中的最小值的一半,而上限为所有重构幅值与理论幅值之中的最大值。两个“+”表示真实的双声源位置。 从图3(a)~图3(c)可以看出,基于无约束L1/2正则化方法进行声源识别时,声源识别位置严重偏离真实声源位置,说明方法失效,而添加强约束条件后,声源识别结果与理论值之间十分吻合。 出现这一现象的原因是,当测量数据中包含大量噪声,难以有效地区分出噪声成分与目标信号成分时,为了使得拟合得到的近似解与精确解之间无限逼近,L1/2正则化方法模型倾向于给出由代表最重要特征的少数权重构成的拟合结果。由于模型强烈依赖于少数特征,代表这些凸出特征的权重量级往往较大。与此同时,由于解范数值的增大,拟合模型变得很不稳定,泛化能力大大降低,容易产生过度拟合,进而导致声源识别失效。 因此,本文通过对等效源强解范数添加强约束,平衡约束值所带来的放大误差以及近似解与精确解之间的误差,使得问题在约束允许误差范围内寻到最优解。为了更清晰地展示添加约束前后求解得到的等效源强差异,画出有/无约束时的121个等效源强的幅值对比曲线,如图4所示。 图4 有/无约束L1/2正则化的等效源强对比Fig.4 Comparison of equivalent source strengths for constrained / unconstrained L1/2 regularization 从图4可以看出,在添加约束条件之前,大部分等效源强度较高,且分布无规律,说明在噪声成分的影响下,并没有达到稀疏化的效果。添加约束条件后,大部分等效源强都趋近于0,仅有2个分布在真实声源附近的主峰凸显出来。为了更清晰地展示残差范数、解范数与声源识别误差之间的内在联系,将添加约束前后的解范数、残差范数与声源识别误差列于表2。 表2 添加约束前后的方法对比Tab.2 Comparison of methods before and after adding constraints 从表2可以直观看出,无约束下的L1/2正则化方法虽然可以实现较小的残差范数,但解范数也随之增大,而添加约束条件后,限制了解范数的无限增大,同时通过强制稀疏化可以去除代表噪声成分的等效源强系数,因此声源识别误差更小,说明此约束条件合理有效。 为验证方法的有效性,分别将本方法与传统基于Tikhonov正则化的ESM方法、(迭代加权等效源)IWESM方法、(宽带声全息)WBH方法、基于L1正则化[42]的CESM(压缩感知等效源法)等方法进行对比验证。需要说明的是,被比较的方法都采用的是该方法的最优参数,对于Tikhonov正则化,通常基于L曲线法确定正则化参数,而对于稀疏正则化方法,通常基于交叉验证法确定正则化参数η。 (1)声源识别精度分析。为了分析新方法的声源识别精度,讨论了声源定位误差errorloc和幅值重构误差erroramp随着分析频率f和测量距离L的变化,将结果列于表3和表4中。为了更清晰地展示不同方法的区别,在表5中给出L=0.25 m部分频率下的声源识别结果。同时,为了更加直观地展示方法性能,将声源定位误差errorloc和幅值重构误差erroramp分别在图中的上方和下方标出,若声源定位准确,则仅标记其幅值重构误差。当声源个数与真实情况不符,则判定方法失效。 表3 双声源定位误差Tab.3 Positioning errors of two sound sources 表4 双声源幅值重构误差Tab.4 Amplitude reconstruction errors of two sound sources 表5 声源识别结果(RSN=30 dB,L=0.25 m,R=0.24 m,LR=0.05 m)Tab.5 Sound source identification results(RSN=30 dB,L=0.25 m,R=0.24 m,LR=0.05 m) 从表3~表5可以看出,本文提出的有约束L1/2-ESM方法始终能够保持较低的声源幅值重构和定位误差,即使当测量距离增大或者声源频率降低时,声源识别误差依然维持在20.00%以内。这是因为,在等效源强求解中引入L1/2稀疏无偏约束来准确提取声场特征的同时,添加强约束条件以防止模型过拟合,使得有约束L1/2范数相比其他正则化提供了更加准确和稳健的结果。 从表3~表4可以看出,传统方法的声源识别精度随着测量距离的增大和声源频率的降低而显著下降。其中,ESM和IWESM方法在频率为1 000 Hz以上时,声源识别误差维持在20.00%以内,而对于1 000 Hz以下的频率,在测量距离0.15 m以上时,识别误差有明显的提升,高达40.00%;CESM的最低适用频率为500 Hz,适用测量距离为0.15 m以下;WBH对于声源频率更为敏感,适用的最低频率仅为1 500 Hz左右,在测量距离为0.15 m以上时,对于1 500 Hz以下频率的声源定位误差甚至达到50.00%,说明该方法在中高频范围内才能获得理想效果。 表5显示,当测量距离增至0.25 m时,ESM与IWESM的云图中虽然能够大体显示出100 Hz双声源位置,但受到分辨率限制,结果可读性较差且幅值耗散严重。对于630 Hz双声源,则没有成功辨识。CESM与WBH在1 000 Hz以下频率的识别热点合为一片,且重构幅值过高。出现上述现象的原因是,ESM与IWESM方法不具备稀疏特性,源强能量的耗散导致重构幅值整体偏低。CESM是基于L1解框架提出的,但是其稀疏性有限,仍不足以分辨主瓣较宽的低频声源,同时,模型的过度拟合导致源强幅值偏高。WBH算法中的第一个最陡下降方向寻优相当于延迟求和(delay and sum, DAS)波束形成过程,因此WBH第一次迭代过程的分辨率与DAS相当,对于中低频率,容易在中心位置产生热点声源,在迭代过程中,WBH是在第一次迭代的基础上进一步迭代更新,而中心声源仍然存在,进而产生了错误的识别结果,仅在1 500 Hz以上能够保持良好的性能。 (2)分辨率性能分析。除了声源定位与幅值重构准确性以外,空间分辨率也是反映算法性能的一个重要指标,代表算法能够区分邻近两个声源的最小距离R,R值越小,则算法的分辨率越高。本文讨论了最小可分离源间距R随着分析频率f和测量距离L的变化。将重构面设在声源表面,当能够有效地分离出两个间隔为R/m的双声源时,规定R值下限即为当前工况下的分辨率上限。设置声源间距R从0.08 m开始,以0.04 m幅度依次递增,上限为0.5 m,结果如表6所示。同时,用“○”记号,分别在该频段内,最低频率100 Hz以及最高频率2 000 Hz的极限位置处标记出分辨率的值。 表6 分辨率性能分析结果Tab.6 Analysis results of resolution performance 从表6可以看出,新方法获得了最优异的分辨率性能,具体来说:当测量距离最近为0.05 m时,对于100~2 000 Hz全频段声源,本方法的分辨率均可以达到0.08 m,对应于最低频率100 Hz波长的1/43,而当测量距离增至0.25 m时,本方法的分辨率最大值0.20 m出现在125 Hz及以下频率,对应于此频段内最高频率125 Hz波长的1/17。综上,在0.25 m测量距离范围内,本文方法的分辨率在分析频段信号波长的1/43~1/17之间。这得益于引入了有约束稀疏正则化L1/2范数,相比L1范数,L1/2范数可以对非零元素施加更为均匀的惩罚,保留了声场重要特征信息的同时,抑制了与噪声成分相对应的等效源强分量,大大提高了分辨率性能。 而对于传统方法,按照上述分析过程,ESM和IWESM的分辨率较为接近,在0.25 m测量距离内,分辨率为信号波长的1/28~1/14。CESM虽然具备一定程度的稀疏性能,但L1范数最小化的惩罚不均匀性和对重尾分布噪声的敏感性导致该算法不适用于远距离测量,分辨率随距离增大而下降严重,且性能不稳定,分辨率整体在信号波长的1/43~1/8。对于WBH,在中低频率范围内的声源识别能力有限,而对于1 500 Hz以上的声源频率,分辨率最优也仅能达到信号波长的1/14。 (3)抗噪性能分析。在基于传声器阵列进行声源识别的实测过程中,通常存在难以控制的噪声干扰,影响目标声源的有效辨识。为了验证本方法对于噪声的抗干扰性能,进一步降低频域信噪比。结果发现,当频域信噪比大于或等于15 dB时,本方法可以输出最好的声源识别效果,而当信噪比进一步降低时,本方法与CESM方法性能相当。这是因为当干扰噪声影响较大时,信号的空间稀疏特性受损,此时L1/2范数相对于L1范数的稀疏约束优势逐渐缩小。可见,在大部分实测环境噪声水平范围内,本方法可以在位置和幅值估计方面提供最为准确的声源识别结果。 以RSN=15 dB/L=0.10 m/R=0.24 m/LR=0.05 m的测试工况为例,对比不同方法的声源识别效果差异。由于篇幅限制,此处以630/1 000 Hz为例,将结果列于表7中。 表7 声源识别结果(RSN=15 dB,L=0.10 m,R=0.24 m,LR=0.05 m)Tab.7 Sound source identification results(RSN=15 dB,L=0.10 m,R=0.24 m,LR=0.05 m) 由表7可以看出,当进一步降低信噪比至15 dB时,新方法的声源识别误差仍然保持在5.00%以内,这说明该方法对于背景噪声的鲁棒性较强。相比而言,ESM和WBH方法没有成功识别出双声源位置,IWESM和CESM方法虽然实现了成功辨识,但是幅值重构精度偏低。 为了模拟实际工程测试情况,由计算机驱动两个扬声器同步产生相同频率,随机幅值大小的正弦信号,由此来验证方法对于双声源识别的有效性。同时,在传声器阵列的另一侧布置了一个噪声源,发射与双目标扬声器相同频率的单频噪声,与双扬声器同时发声进而形成噪声环境。 基于P-U传声器阵列高精度扫描装置采集信号,线性阵列包含9个麦克风,间距0.04 m,扫描得到9×9=81个点。同时布置1个位置不变的参考传声器,对非同步采集信号进行相位校正。试验布置如图5所示,实测工况如表8所示。设定固定信噪比噪声的操作步骤如下:首先,将代表目标信号的双扬声器发声,由传声器阵列采集声信号,计算所分析的频点处的功率大小;然后,关闭双扬声器,打开传声器阵列背侧的代表噪声信号的扬声器,通过调整代表噪声信号的背侧扬声器的声功率,设置15 dB信噪比噪声;最后,在定位试验的数据过程采集中,同时打开双目标扬声器和背侧的噪声源,通过扫描测量采集背景噪声干扰下的声信号。需要说明,为了控制单一变量进行分析,在频率和测量距离适用性分析的验证试验中,干扰扬声器不发声。 表8 双声源试验工况设置Tab.8 Parameters setting of double sound source experiments 图5 声源识别试验布置图Fig.5 Layout of sound source identification experiments 采用基于NI-PXIe总线的数据采集系统完成数据采集,采样频率设为44 100 Hz。理论真值同样通过传感器阵列直接测量得到,验证声源识别准确性。 首先说明添加约束条件的必要性,与仿真部分相对应,给出添加约束前后,L=0.10 m/R=0.24 m/f=1 000 Hz/LR=0.05 m的声源识别结果。 由图6(a)和图(b)可以看出,当未添加约束条件时,基于传统L1/2正则化方法无法得到合理的声源识别结果,且整体幅值异常高,而添加约束条件后,得到了较为理想的声源识别结果。计算可知,未添加约束条件时,残差范数在迭代过程中已经降至1.7×10-8,但解范数却放大至0.02。添加约束条件后,残差范数达到1×10-3,而解范数降至3.3×10-4,试验结果进一步验证了在稀疏正则化基础上添加约束条件的必要性。 图6 有/无约束L1/2正则化声源识别结果与真值对比Fig.6 Comparison between theoretical values and sound source recognition results based on constrained / unconstrained L1/2 regularization of the measured part 接下来,验证方法对于频率的适用性,识别误差如图7所示。用同标记符虚线画出多频下的平均误差。 图7 双声源识别误差Fig.7 Identification errors of two sound sources 需要说明,IWESM方法是在ESM的基础上增加强制滤波以去除虚假声源,二者的实测结果较为接近,在实测部分不再单独列出ESM的结果。从图7中可以看出,对于声源定位误差,传统方法中IWESM表现最为优异,平均误差为4.68%,而本方法为3.43%;对于幅值重构误差,传统方法中CESM表现最为优异,平均误差为18.28%,而本方法降至9.37%。为了更清晰的对比不同方法的结果差异,将100 Hz/630 Hz /1 000 Hz /2 000 Hz的识别结果列于表9中。与仿真部分相同,颜色深浅代表质点振速幅值大小,同时将声源定位误差和幅值重构误差分别在图中的上方和下方标出。 表9 不同测量距离的部分声源识别结果(R=0.24 m,LR=0.05 m)Tab.9 Partial sound source identification results at different measurement distances(R=0.24 m,LR=0.05 m) 实测环境并非理想的自由场环境,测量信号中存在地面与墙面反射、随机干扰噪声等,当测量距离增大时,声源信号至传声器之间的传播路径会更加复杂,传声器在接收到目标信号的同时,会接收到更多的干扰噪声,进而会降低目标信号的信噪比。另外,且测量到的倏逝波成分随测量距离的增大呈指数下降,大大增加了基于声全息法的声源识别难度。为了进一步验证方法对于测量距离的适用性,以630 Hz /1 000 Hz频率为例,将0.15 m/0.25 m测量距离下的声源识别结果列于表9中。 从表9可以看出,本方法在不同测量距离下均有效识别出了双声源。当L增至0.15 m时,声源定位和幅值误差基本维持在20.00%以内。当L进一步增至0.25 m,定位误差在15.00%以内,幅值重构误差在25.00%以内。结果表明,即使在测量距离增大的情况下,本算法也能实现较为准确的声源定位和良好的幅值量化。需要说明,当测量距离增大时,个别工况下的识别误差偏高,分析原因如下:首先,喇叭本身的发声属性导致测量信号具备一定的随机性,喇叭在个别频率下的发声性能略差,会导致不同频率声源识别效果之间存在差异。更重要的是,本方法是基于压缩感知理论提出的,当测量距离增大时,相邻传感器接收信号的差距缩小,测量矩阵的有限等距属性(restricted isometry property,RIP)变差,增加了求逆过程的不适定性。但是,相比传统方法,本方法仍能输出最优的识别结果。 对于传统算法,随着测量距离的增大,均呈现出不同程度的失效,甚至难以判定声源位置。具体而言,对于IWESM方法,当L增至0.15 m,定位误差在20.00%以内,但是幅值误差高达48.00%。在0.25 m测量距离时,方法失效。对于CESM方法,当L增至0.15 m时,630 Hz声源识别结果中出现严重的鬼影,且识别源位置严重偏离真实位置,而对于1 000 Hz声源的幅值重构误差为21.00%,定位误差接近27.00%。对于WBH方法,当测量距离增至0.15 m时,同样无法辨识630 Hz频率所对应的两个热点位置。对于1 000 Hz声源,定位误差接近20.00%,幅值重构误差则达到32.00%。对于0.25 m距离,方法失效。上述结果表明,传统等效源方法对于测量距离较为敏感,最远测量距离为0.10 m左右。 以630 Hz/1 000 Hz为例,验证方法的抗噪性能,将声源识别结果列于表10中。由表10可以看出,当减小信噪比至15 dB时,仅有本方法的误差仍可以维持在15.00%以内,而其他传统方法在噪声的影响下,声源识别误差均有不同程度的增大。 表10 信噪比RSN=15 dB的声源识别结果(R=0.24 m,L=0.10 m,LR=0.05 m)Tab.10 Sound source identification results with RSN=15 dB(R=0.24 m,L=0.10 m,LR =0.05 m) 以1 000 Hz为例,验证方法的分辨率性能,并将归一化后的声源定位结果列于表11中。由表11可以看出,当缩短双声源间距为R=0.08 m时,仅有本方法成功分辨出了双声源位置。相比而言,传统方法的声源分辨能力较差。在L=0.10 m时,IWESM与WBH的热点位置出现在两个真实声源之间,无法辨识双声源位置。CESM出现多个鬼影,表示方法失效。在L=0.15 m时,CESM分辨出的声源位置严重偏离真实位置,且其中一个声源幅值偏低,容易视为旁瓣或鬼影,识别结果可读性较差,而其他方法均只出现一个热点位置。 表11 双声源间隔R=0.08 m的声源识别结果(f=1 000 Hz,LR=0)Tab.11 Sound source identification results with double sound source spacing R of 0.08 m(f=1 000 Hz,LR=0) 为了更加清晰直观地对比本文提出算法与传统算法的性能差异,根据仿真与实测结果,将不同方法能够保持良好稳定性能时的最低可测频率、分辨率上限值、最远测量距离(声源识别误差在25.00%以内认为识别有效)等多方面的性能指标进行定量对比,列于表12中。 表12 不同方法性能对比Tab.12 Performance comparison of different methods 由表12可以看出,在最低可测频率方面,传统方法对于500 Hz及以上的频段稳定性较好,而本文方法可以将分析频率下限扩展至100 Hz;在分辨率方面,CESM方法与本文方法由于具备稀疏特性,对于100 Hz的上限均为0.08 m(双声源紧靠),但是CESM方法在全频段内的表现并不稳定;在最远测量距离方面,传统方法在0.10 m测量距离以内表现稳定,而本方法在0.25 m以内可以实现较高的声源识别精度。 针对传统等效源方法对于空间稀疏分布声源识别精度低、稳定性不足的问题,提出了一种基于有约束L1/2范数稀疏正则化的声源识别方法。新方法以Tikhonov正则化的解范数作为约束条件,同时对源强求解过程进行强稀疏化处理,避免了传统最小二乘拟合模型存在的能量耗散,以及传统稀疏正则化拟合模型容易过度拟合的问题,从而有效提高了声源识别的精度与稳定性。 开展了双声源识别的仿真模拟试验,结果表明,当基于无约束L1/2范数进行声源识别时,声源识别误差较大,以L=0.10 m/R=0.24 m//f=1 000 Hz/LR=0.05 m工况为例,声源定位误差为20.83%,幅值重构误差为5.29%,而添加约束条件后,通过抑制模型过拟合保证了强稀疏性,声源定位误差降至0.08%,幅值重构误差也降至2.48%,说明了对稀疏L1/2正则化添加约束条件的必要性和有效性。 在普通室内环境中,对两个扬声器声源开展了噪声测试研究。试验数据表明,在测量距离0.25 m以内时,本文提出的方法对于100~2 000 Hz声源的定位和幅值重构误差始终维持在25.00%以内,而传统方法所适用的最远测量距离仅为0.10 m左右,仅在500 Hz以上能够保持良好的性能。进一步,当缩短双声源间距,仅有本方法成功识别出间隔0.08 m的双声源位置。可以看出,相比传统方法,本方法对于中低频声源识别精度更高。如何在更远距离、更低信噪比的测量情况下进一步提高方法的精度,是本文下一步需要重点开展的工作。1.2 有约束的范数正则化
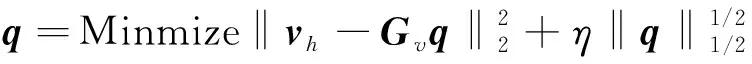

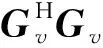
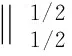
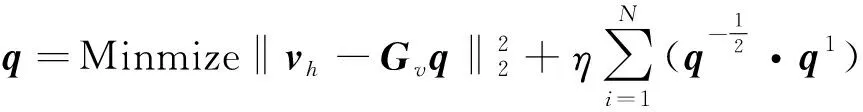
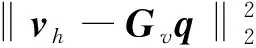

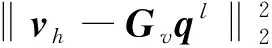
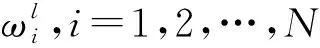
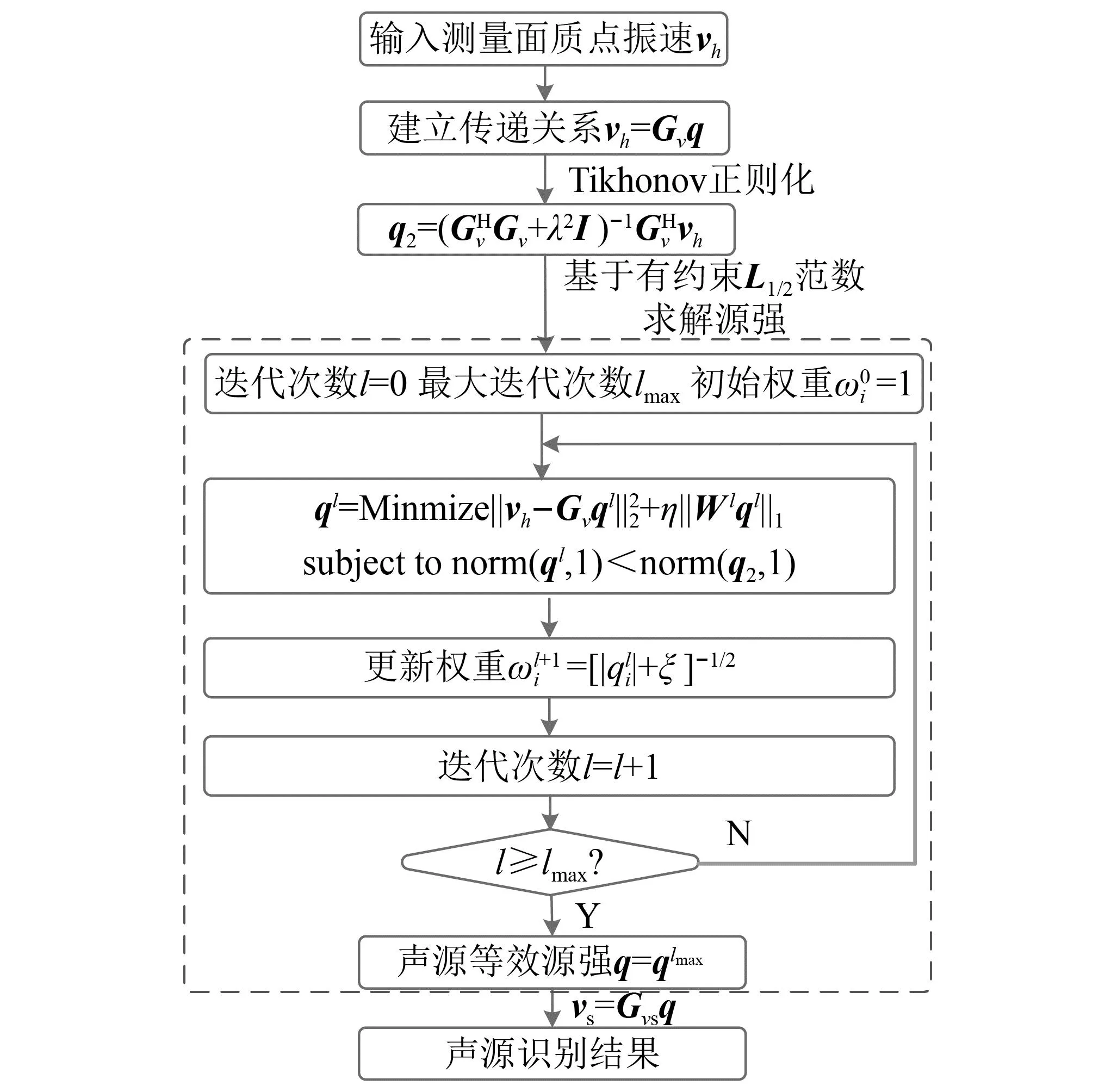
2 仿真计算
2.1 仿真环境及试验参数
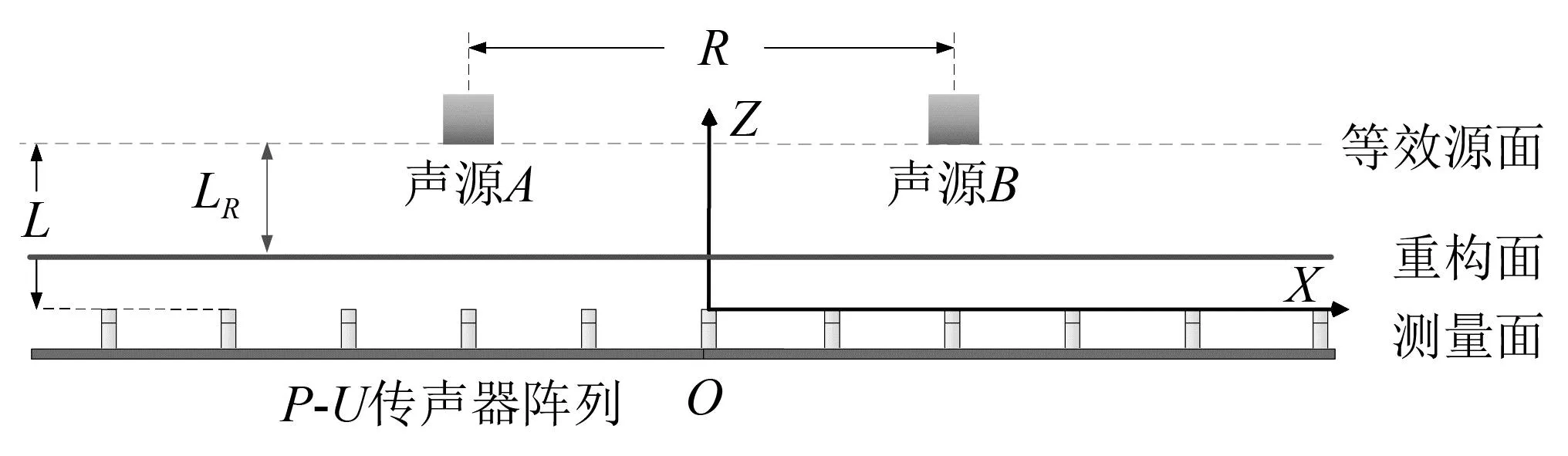
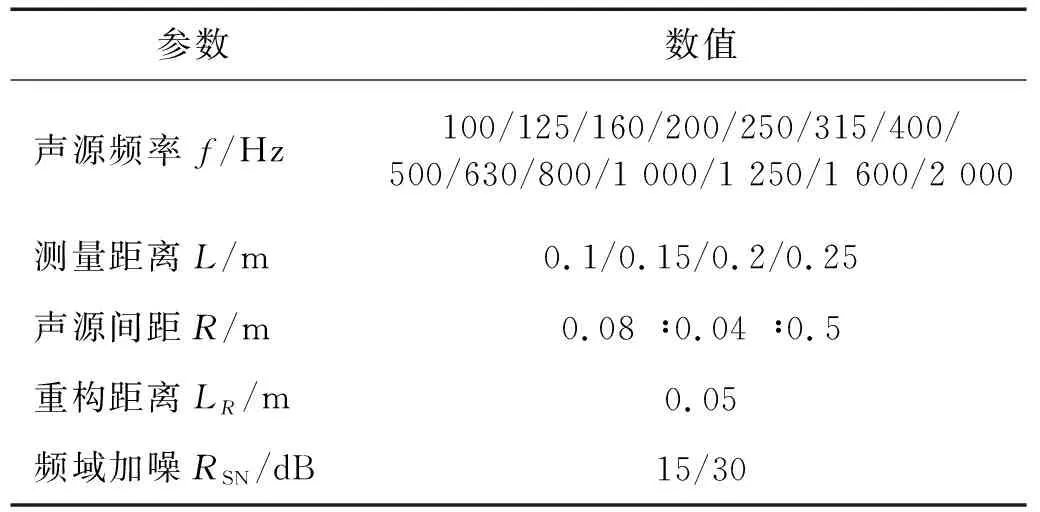
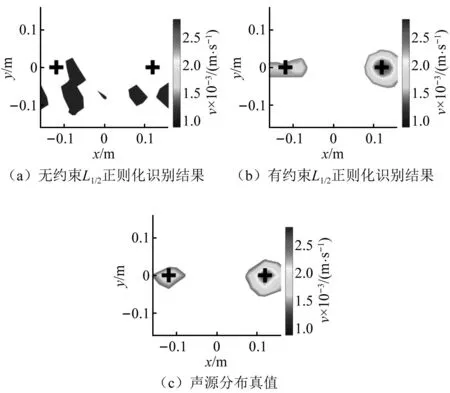
2.2 稀疏正则化约束的必要性讨论
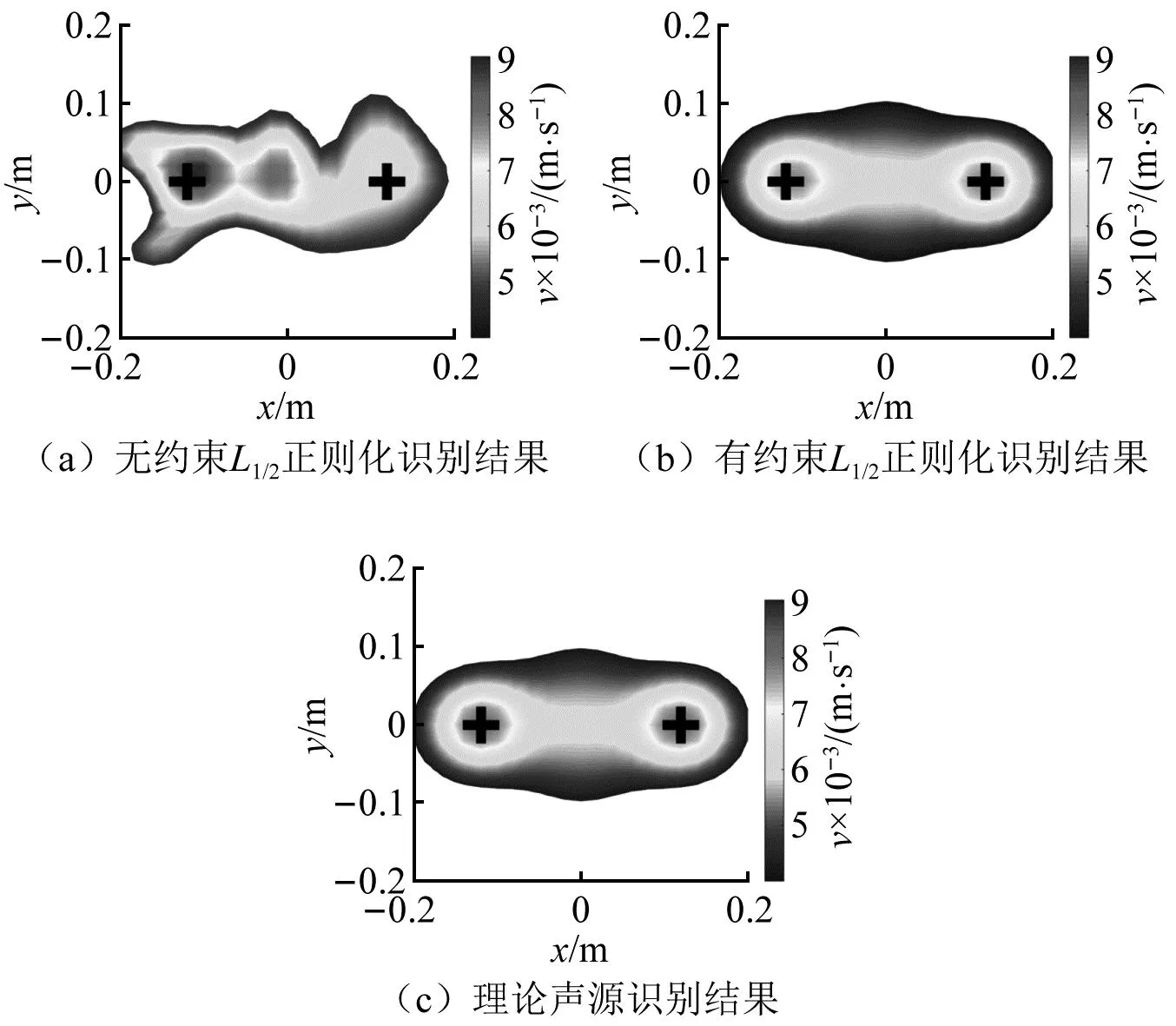

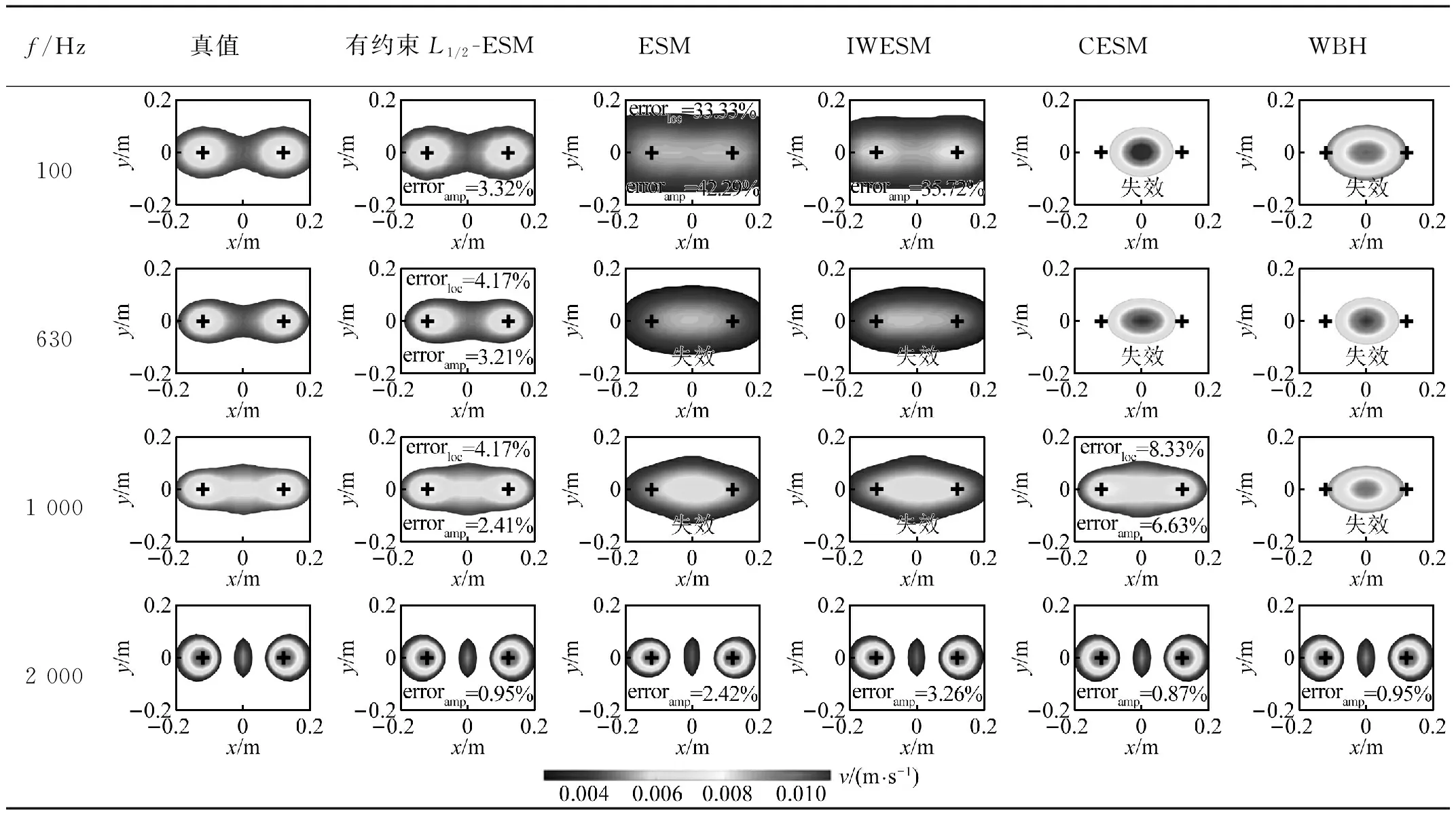
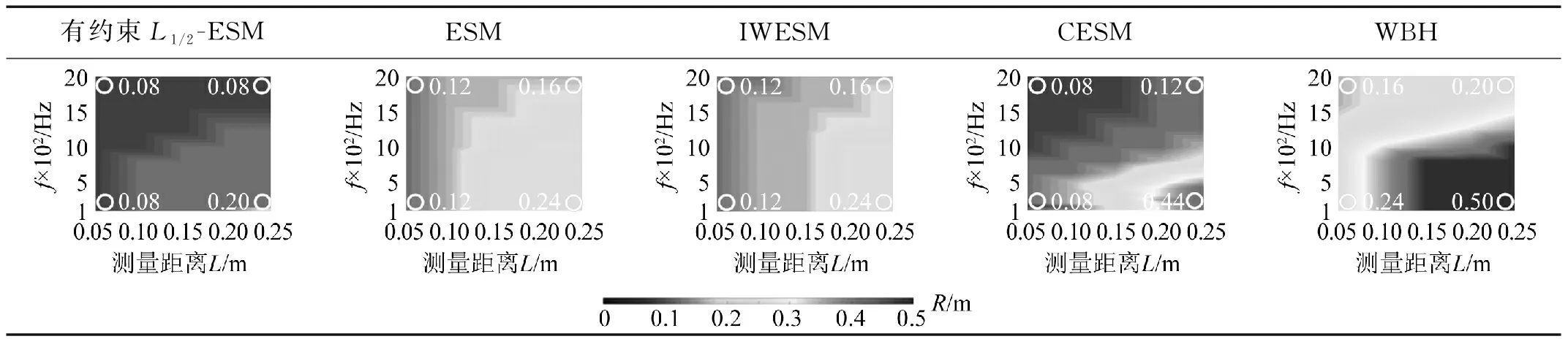
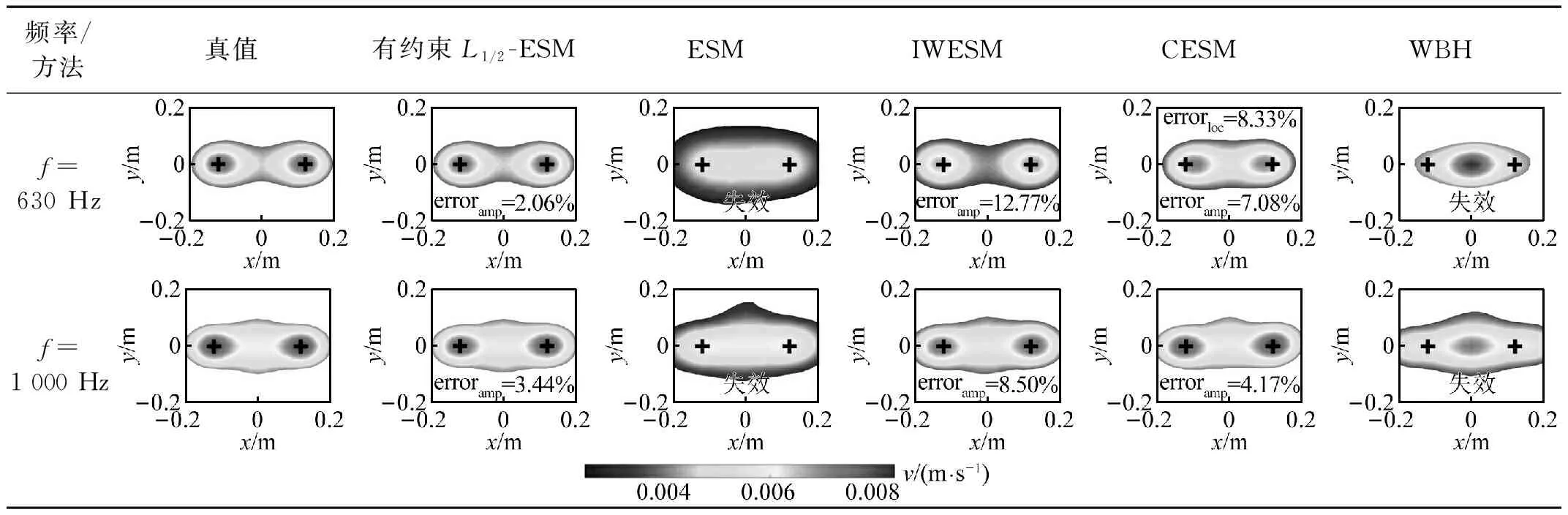
2.3 试验参数讨论
3 实测试验验证
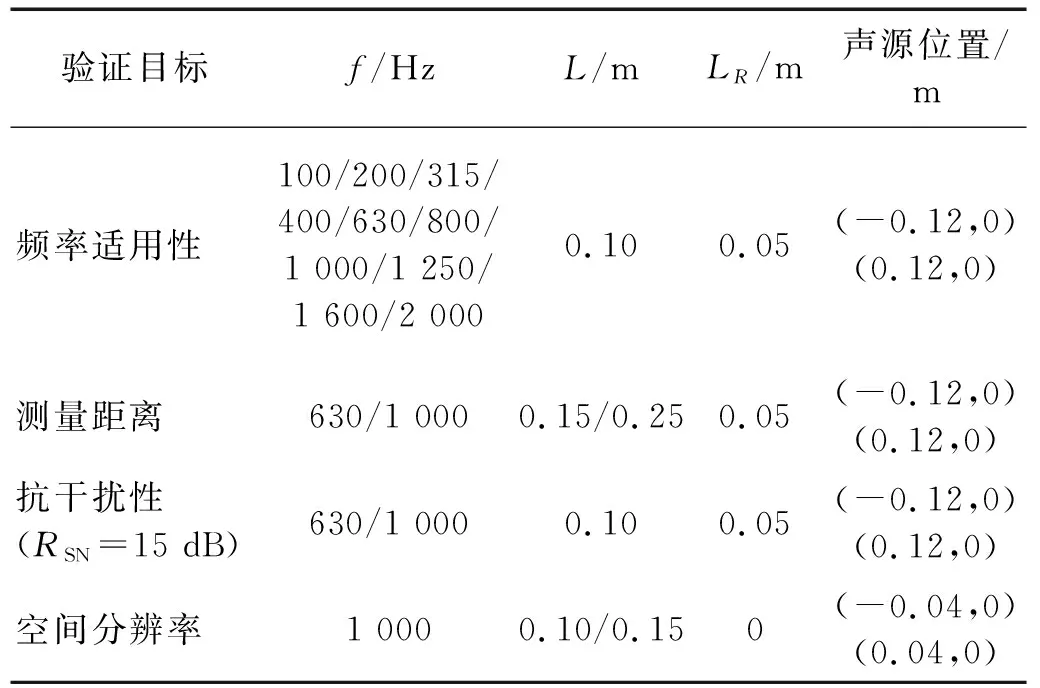
3.1 试验设置

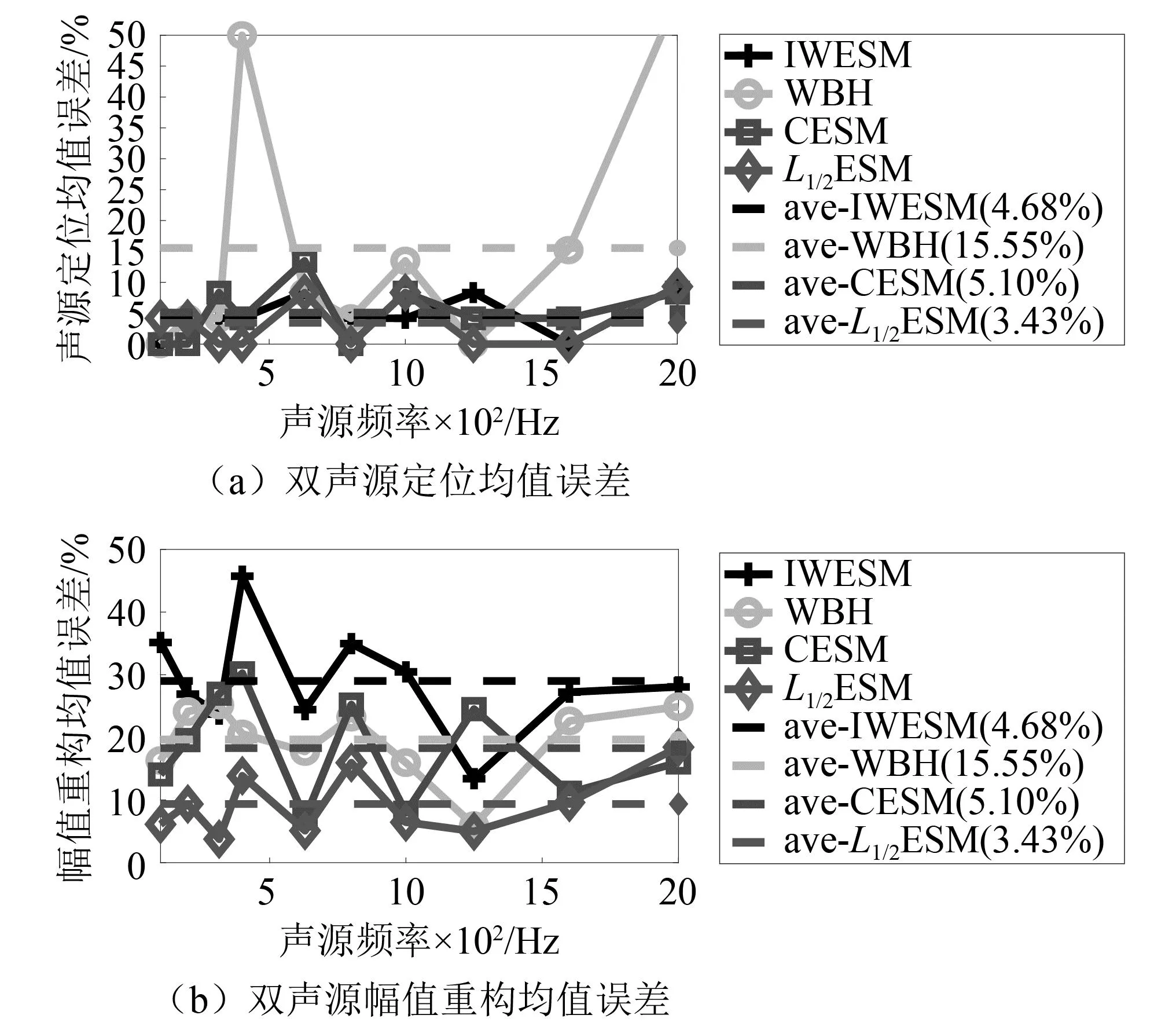
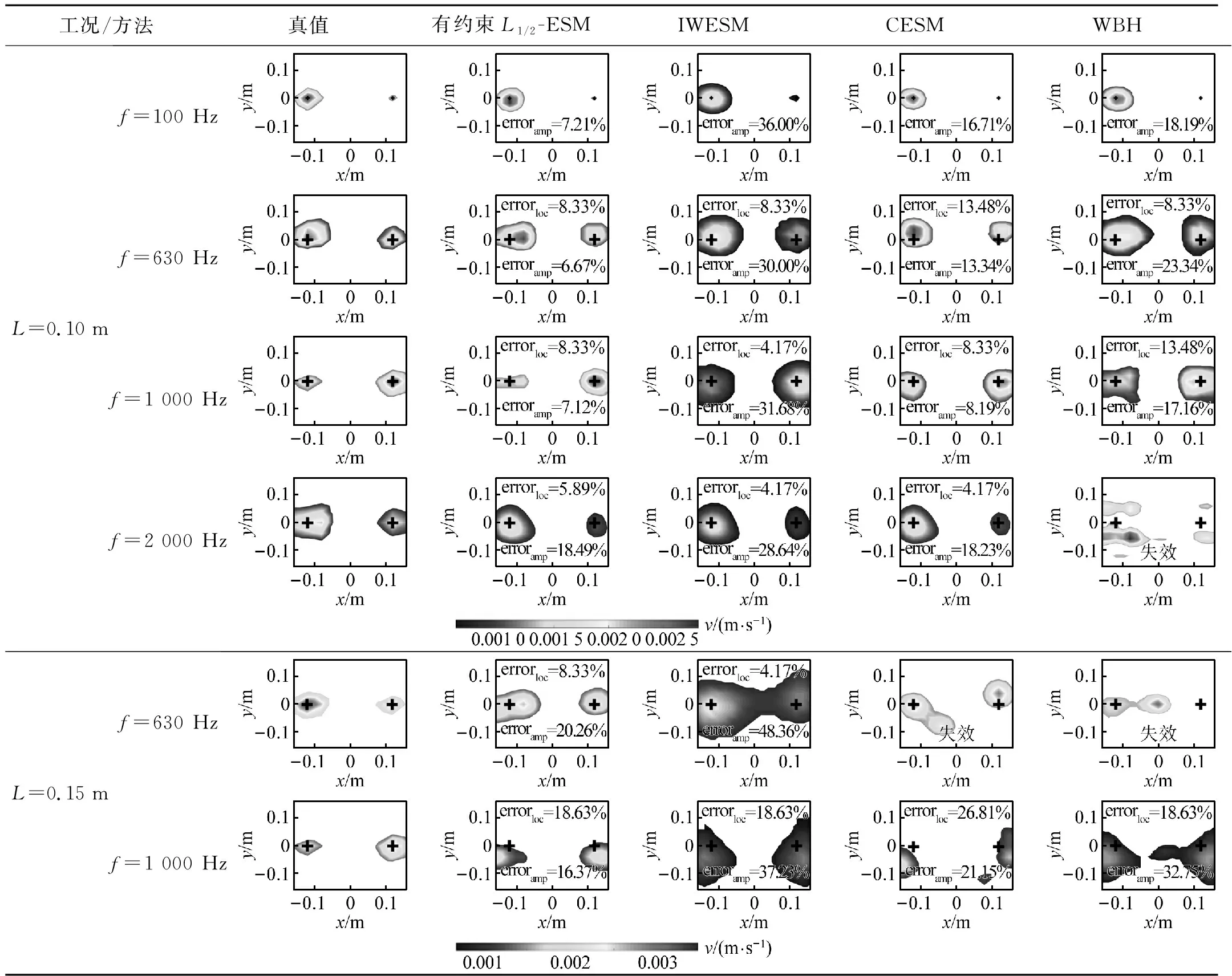
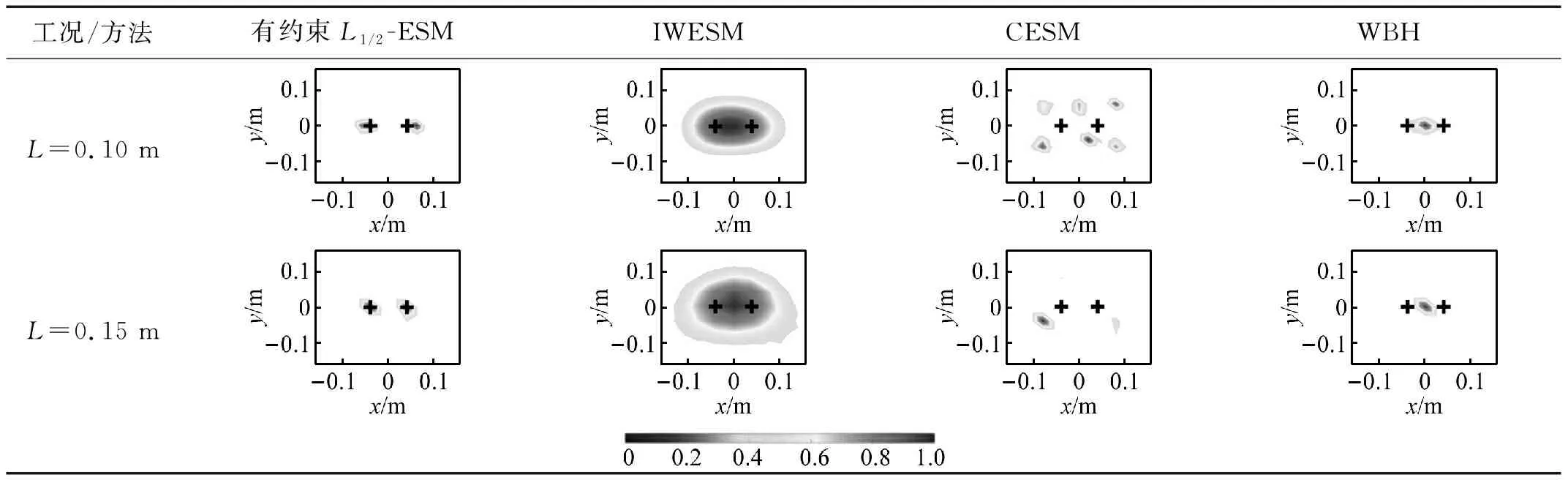
3.2 声源识别结果

4 结 论

