非定常空化涡旋结构演化及压力波机制的研究

王子豪, 孙铁志, 张桂勇,2

(1. 大连理工大学 工业装备结构分析国家重点实验室 船舶工程学院,辽宁 大连 116024;2. 高新船舶与深海开发装备协同创新中心,上海 200240)

当液体中的局部压力降到局部饱和蒸气压以下时,液体由液相转变为气相,这种相变现象称为空化[1]。空化几乎包括所有复杂流动的物理现象,例如相变、多相湍流、非定常性和可压缩性。空化气泡在高压梯度下的剧烈崩塌会产生高压冲击和复杂的涡流结构,这通常会引起一些不良影响,例如螺旋桨空蚀、噪声以及水力机械振动和压力脉冲[2-4]。

考虑到空化在船舶推进中的广泛应用和巨大挑战,研究人员[5-7]已经进行了很长时间的研究,尤其对空化的动力学行为进行了广泛的讨论。以水翼模型为例,当空泡在水翼表面闭合时,此空化过程被称为局部空化。在局部空化下,片状空泡会周期性的过渡到云空泡,这种周期性的过程的主导机制是十分复杂的。王巍等[8]综合应用试验和数值模拟,详细分析了绕水翼云空化流动的发展机理,结果表明逆压梯度是回射流产生的原因,回射流对空泡存在的剪切作用导致空泡脱落。除了经典的回射流外,激波导致空泡脱落的机制近年来已得到广泛认可。Arndt等[9]在2001年研究了不同参数(σ/2α)下绕NACA0015水翼的空化流动,结果观察到了两种空化流动机制。在σ/2α高时回射流是空泡脱落的原因,而在较低的σ/2α时,激波主导着空化流动。Ganesh等[10]在2016年以楔形体为模型进行了空化试验,利用X射线密度法测量了空化流场,除了经典的回射流机制被观察到,在低空化数下空泡内向上游行进的激波交界面清晰可见,当激波到达楔形体的顶点时,大尺度的云空泡被夹断,这表明激波机制占主导地位。尽管如此,学者们在激波发生的原因上存在分歧。Ganesh等认为可压缩性是激波产生的原因。Bhatt等[11]认为激波是先前脱落的云空泡溃灭产生的压力波撞击空泡后缘触发的。Zhang等[12]对激波产生的两种分歧原因进行了详细的区分,通过试验发现了在未发生先前脱落的云空泡溃灭的情况下出现了激波的产生。因此空泡溃灭并不是激波产生的必要条件,而是一种独立的空化流动机制,称为压力波机制。这纠正了之前学者们对空化流动的不恰当分类。Leroux等[13]在NACA66(mod)水翼上观察到了两种准稳定的局部片状空泡,与高Strouhal数条件下的回射流机制不同,低Strouhal数的空化动力学主要由云空泡溃灭形成的压力波的传播主导。尽管对空化机制的研究已经取得了丰富的成果,但是更多的讨论集中在回射流机制和激波机制上,对于压力波机制的作用机理的揭示仍然很少,需要进一步研究空化流动的特性和动力学。

空化流动的数值模拟主要包括不可压缩方法和可压缩方法。空化流场中主流的纯液体介质具有高声速和低马赫数的特点,因此对于大多数的空化流动的数值计算都基于不可压缩方法[14-15],该方法假定液体和蒸气的密度恒定。但是两相混合物的声速比其组成相的声速小几个数量级,这导致空化流场中出现更高的马赫数,当声速与流速相当时,空化则是具有高度可压缩性的流动现象[16]。考虑到压力波现象与声学特性之间的密切关系,需要采用可压缩空化模拟方法。王畅畅等[17]使用可压缩方法进行数值模拟,详细分析了压力波机制下的空泡脱落过程,结果表明云空泡溃灭是压力波出现的原因,压力波的传播会延迟空泡脱落的周期。湍流模型对于捕获空化演化的不稳定细节至关重要。雷诺平均纳维-斯托克斯(Reynolds-averaged Navier-Stokes equations,RANS)方法具有良好的稳定性、合理的计算成本和可接受的精度的优点,因此它在实际工程中被广泛使用。尽管RANS方法非常流行,但是时间平均过程会滤除湍流光谱,这会导致湍流黏度过度预测的问题[18-19]。大涡模拟(large eddy simulation,LES)模型可以预测流场的不稳定特性,但是它需要非常精细的网格和很小的时间步。因此,数值模拟的计算成本非常高。分离涡模拟(detached-eddy simulation,DES)模型是一种混合湍流建模技术,近壁区域通过RANS处理和远壁区域由LES处理,因此DES已成为基于RAN的湍流模型和LES之间的潜在折中方案[20-21]。

近年来,人们进行了更多的试验或数值努力来探索局部空化的详细涡旋结构。Ji等[22]分析了3D水翼上空化脱落的马蹄形涡旋结构,捕获了主要和次要的U形空泡云。Sun等[23]利用涡量运输方程分析了斜压矩项、涡量拉伸、膨胀项和流涡旋黏性项对空化演化的影响。空化是一种复杂的流动现象,具有多尺度特性,因此可以将其理解为在多个固定频率下的流动行为的组合。对于空化流的复杂空化-涡旋相互作用,揭示相干湍流结构具有重要意义。

流场可被分为不同的流动模态,每个模态都有其各自的动力学特性。本征正交分解(proper orthogonal decomposition,POD)法和动力学模态分解(dynamic mode decomposition,DMD)法已被广泛用作数据驱动算法,来识别多尺度相干结构的时空特性。POD方法可以有效地确定能量最高的流动结构,通过模态所含能量的多少判断流场中的主要模态,但是并不能清晰地提供各个相干模态的频率信息,这是由于在同一模态中,可能含有多种频率的成分。Schmid[24]基于非线性动力系统的Koopman分析建立了动态模式分解方法。动力学模态分解方法是将模态按照频率大小进行排序,所得到的模态均为单一频率的模态,在对流动特征分析中表现出了强大的优势。许多研究已经证实了DMD方法的效果。Liu等[25]通过分析ALE 15水翼周围的空化流动过程,比较了POD和DMD的差异。他们指出,与POD方法相比,DMD方法更适合分解不稳定的空化流,尤其是在特定的动态模式和相应的特征频率下。谢庆墨等[26]利用DMD方法对空化流动进行了分解以及重构,获得了空化流场的流动结构特性。以上研究丰富了涡旋分析的方法,但是对于压力波机制下的涡旋演变规律却缺少关注。

为了深入研究压力波传播机制的动力学特性和丰富压力波机制下涡旋演变规律,本文采用DES方法模拟了水翼上的非定常空化流动,应用可压缩空化流动求解器研究空化动力学,空化过程由Schnerr-Sauer模型求解。重点分析了涡旋结构的演化和压力波传播的特性,并且使用DMD方法揭示了涡流动力学和相应相干结构的演化。

1 计算模型

1.1 基本控制方程

本文的控制方程是三维可压缩Navier-Stokes方程,它基于均质的多相流模型。可压缩质量守恒方程、动量方程、能量方程的定义分别为

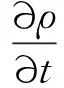
(1)

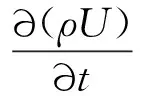
(2)

(3)

式中:U为速度;p为压力;Cp为热力学系数;T为温度。

流体密度ρ,动力黏度μ和热传导率κ定义为

ρ=αlρl+αvρv

(4)

μ=αlμl+αvμv

(5)

κ=αlκl+αvκv

(6)

式中:α为单元内的某一相的体积分数; 下标l为液体; 下标v为水蒸气。

水蒸气采用理想气体状态方程

pv=ρvRvTv

(7)

式中,Rv为气体常数,Rv=461.6 J/(kg·K)。

水的状态方程采用Tait方程[27]

(8)

式中:B=3.06×108;N=7.1; 水的饱和蒸气压力pl,s=2 338 Pa; 饱和密度ρl,s=998.16 kg/m3。

1.2 湍流模型

本文采用SSTk-ωDES模型进行湍流建模,它将边界层中RANS模型的功能与非稳态的分离区域中LES的功能相结合。此DES模型在原始的RANS模型下进行了改进。RANS通过将式(1)～式(3)进行平均获得每个求解变量的平均值和其波动分量。这个过程产生了额外的未知量:雷诺应力项。标准的SSTk-ω模型由Menter等[28]提出, 它基于Bousinessq涡流黏度假设求解雷诺应力项,基于k和ω的两方程模型求解涡黏系数。其中k和ω的输运方程为

(9)

(10)

式中:α,β为经验系数,α=0.44,β=0.082 8;k为湍流的动能;ω为单位耗散率;ui为i方向上的速度;μt为涡黏系数,其表达式为

(11)

(12)

(13)

(14)

式中: Δ为所考虑的网格单元中心与相邻网格单元的网格单元中心之间的最大距离;F1和F2为混合函数,Fs=1-F2。当FDES=1时恢复RANS求解; 当FDES>1时,该求解趋向于LES。

1.3 空化模型

空化模型的输运方程是通过简化并适当地校正Rayleigh-Plesset空泡动力学方程来获得的。本文的空化过程通过Schnerr-Sauer空化模型[29]求解,空化的传质方程为

(15)

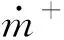
(16)

(17)

式中:Rb为空泡半径;pv为当地温度下的饱和蒸气压,pv=2 338 Pa。空泡半径被定义为

(18)

式中,Nb=1×1013m-3为空泡数密度。

1.4 动力学模态分解法

首先提取非定常流场的数据,并预处理为具有连续快照序列的形式。

(19)

假设矩阵A为快照vi～vi+1的非线性映射的近似,即

vi+1=Avi

(20)

一般情况下,流场的数据快照vi+1的空间位置点数M远远大于快照的总数N,因此矩阵A为高维矩阵,难以进行直接的求解,因此可以建立一个伴随矩阵A进行降维处理。

(21)

(22)

(23)

式中: 矩阵T的列向量是特征向量;Λ为包含特征值λk的对角矩阵。

定义DMD的模态φi为

φi=UT

(24)

定义模态的振幅b为

b=T-1z1=T-1UHv1

(25)

式中,通过奇异值分解将高维系统v1映射到其低维空间z1上。

通过求出DMD模态、特征值和模态振幅,则可以构造未来任意时刻的投影解

(26)

DMD模态的放大率gj和频率ωj可以由特征值λj求解得到

(27)

(28)

1.5 计算域及网格划分

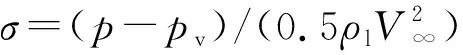
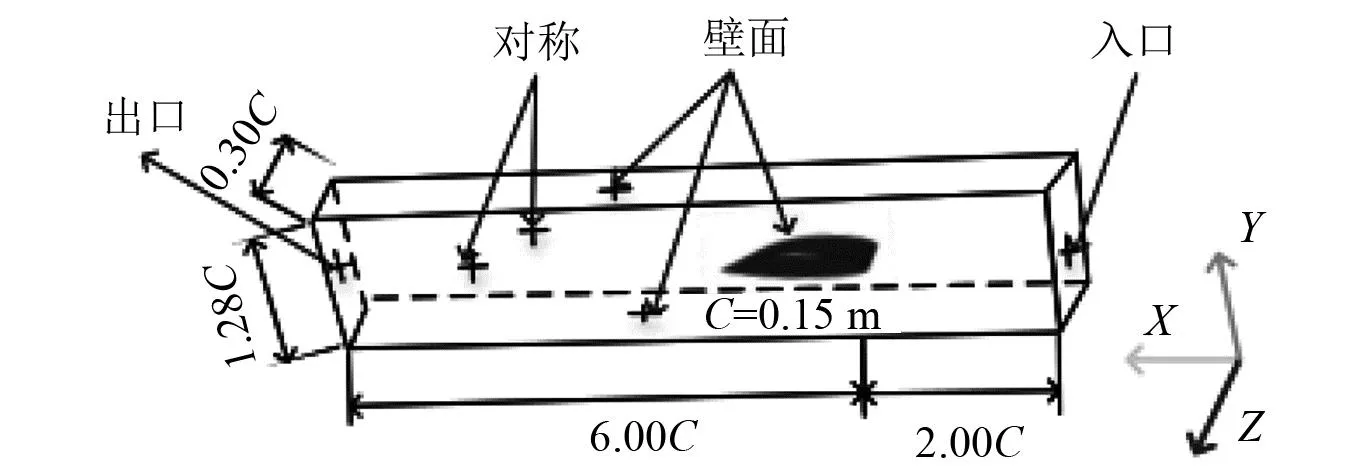
图1 计算域及边界条件Fig.1 Computational domain and boundary conditions

NACA66水翼周围的网格、库朗数和水翼表面的y+值,如图2所示。y+对数值计算的正确性有着重要影响,因此本文的网格设置保证了y+<1,满足分离涡模拟的需求,在水翼表面附近进行不同的网格细化,总网格数量大约为4.5×106。库朗数Co=|V∞Δt/Δx|与收敛速度和计算稳定性密切相关,此计算中使用的物理时间步长为2.5×10-5s,此时间步的设置确保了平均库朗数小于1,这保证了数值计算的稳定性。

图2 NACA66水翼周围的网格、库朗数和水翼表面的y+值Fig.2 Mesh generation, Courant number around the NACA66 hydrofoil and y+ value of the hydrofoil surface

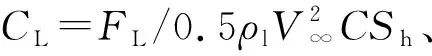
表1 网格无关性验证的结果Tab.1 Results of the mesh independence test

1.6 数值方法的正确性验证

在空泡的生成、生长和溃灭过程中,空化的非定常性会导致水翼的表面压力发生变化。在水翼吸力侧表面的中线处上设置压力监测点,图3(a)中绘制了0.6C位置处压力波动的数值预测和试验测量结果之间的比较,而且标注了一个周期内的8个典型时刻。由图3可知,数值模拟可以很好捕捉空泡溃灭产生的压力波引起的瞬态高压力脉冲。空泡体积随时间的演变绘制在图3(b)中,而且利用水翼体积(Vh=3.64×10-4m3)作为基准对空泡体积进行无量纲化。空泡的体积呈现周期性的变化,数值模拟中的脱落频率是通过对计算域中的总蒸气含量的历史记录进行快速傅里叶变换(fast Fourier transform,FFT)获得的,频率为f=3.73 Hz,已知试验所得的该工况下空泡脱落频率为3.625 Hz,本文计算误差为2.8%,这是一个相对准确的结果。因此,数值模拟可以很好地捕获空化流动的周期性,这表明本文所采用的数值方法可以准确的预测空泡动力学。

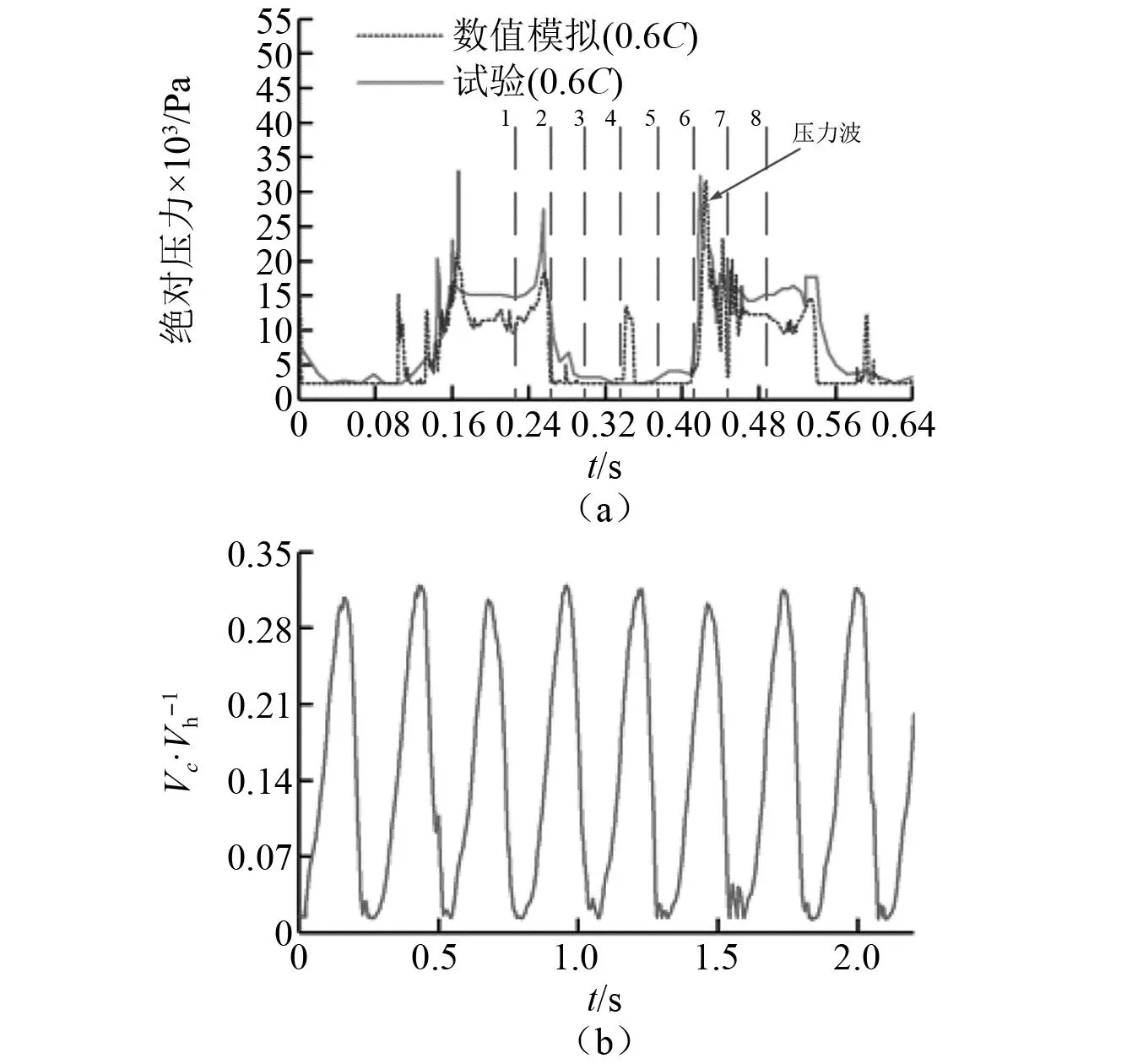
图3 压力波动和空泡体积的演变Fig.3 Pressure fluctuations and evolution of cavity volume

2 结果分析

2.1 非定常空化形态演化过程分析

空化形态的演化是空化流动的重要特征之一。图4显示了一个典型周期内的空泡形态和翼型表面及侧面的压力分布演化,8张图片的瞬时压力特征在图3(a)中进行了标注。由图4可知,数值模拟很好地描述了非定常空泡的演变,空泡的长度和体积有规律地变化。在每次大的空泡脱落结束时,空泡会完全塌陷,但很快就会重新长大,并在新的周期开始之前不久再次收缩。空化演变过程可以分为4个典型阶段:①在t0+0/8T～t0+2/8T时,水翼前缘的平滑的片状空泡逐渐生长,空泡的存在导致水翼上方出现低压区。在t0+2/8T,片状空泡生长到最大值。②在t0+3/8T～t0+4/8T时,空泡的后缘附近近壁面区域产生回射流,回射流运动到水翼前缘时导致片状空泡断裂,产生大尺度云空泡。③在t0+5/8T～t0+6/8T时,云空泡在主流的作用下向下游输运,前缘的片状空泡再次开始生长。当云空泡运动到水翼后缘的高压区时,在内外压差的作用下开始溃灭,同时产生高压压力波。压力波一旦产生,将在流场中传播,高压区域迅速替代水翼上方的低压区,并抑制前缘片状空泡的生长,导致片状空泡溃灭,这代表着高压压力波的传递过程。观察图3(a)的压力波动曲线可以发现,高压压力波的传递过程对应标注6～标注7的区域,压力的波动会出现明显的瞬态高峰值压力脉冲,这说明高压压力波的快速回弹导致水翼表面出现瞬态高峰值压力。④在t0+7/8T时,前缘的空泡再次生长,下一个新的周期开启。

图4 数值模拟和试验结果的一个典型周期内空泡形态的比较Fig.4 Numerically predicted cavity evolution compared with test results over a typical cycle

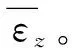
(29)

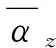
图5 压力波传播过程的4个连续瞬时流场Fig.5 Four consecutive instantaneous flow fields in the pressure wave propagation

为了更直观地量化压力波的传播过程,图6显示了水翼表面0.2C,0.5C和0.8C位置处压力波动的数值预测和试验测量结果之间的比较。压力随着空泡的演变而波动。当监测点被附着的空泡覆盖时,压力按监测点的顺序下降到饱和蒸气压附近。当监测点附件出现孤立的小空泡溃灭时,水翼表面上会产生局部的压力脉动。当大尺度云空泡溃灭在水翼尾部,0.8C位置会先产生高压力脉冲,之后向前传递到0.5C位置。这个过程是瞬时的,因此无法准确地在图6中观察到时间差。但是压力波从0.5C位置传递到0.2C位置可以观察到明显的时间差。这是因为压力波传递过程会存在能量损耗,传递的速度会逐渐降低。这个过程对应着图4的t0+5/8T～t0+6/8T和图5的t0+21/32T～t0+24/32T。其中,图4的t0+6/8T可以观察到压力波传递到0.2C位置的水翼表面的高峰值压力。

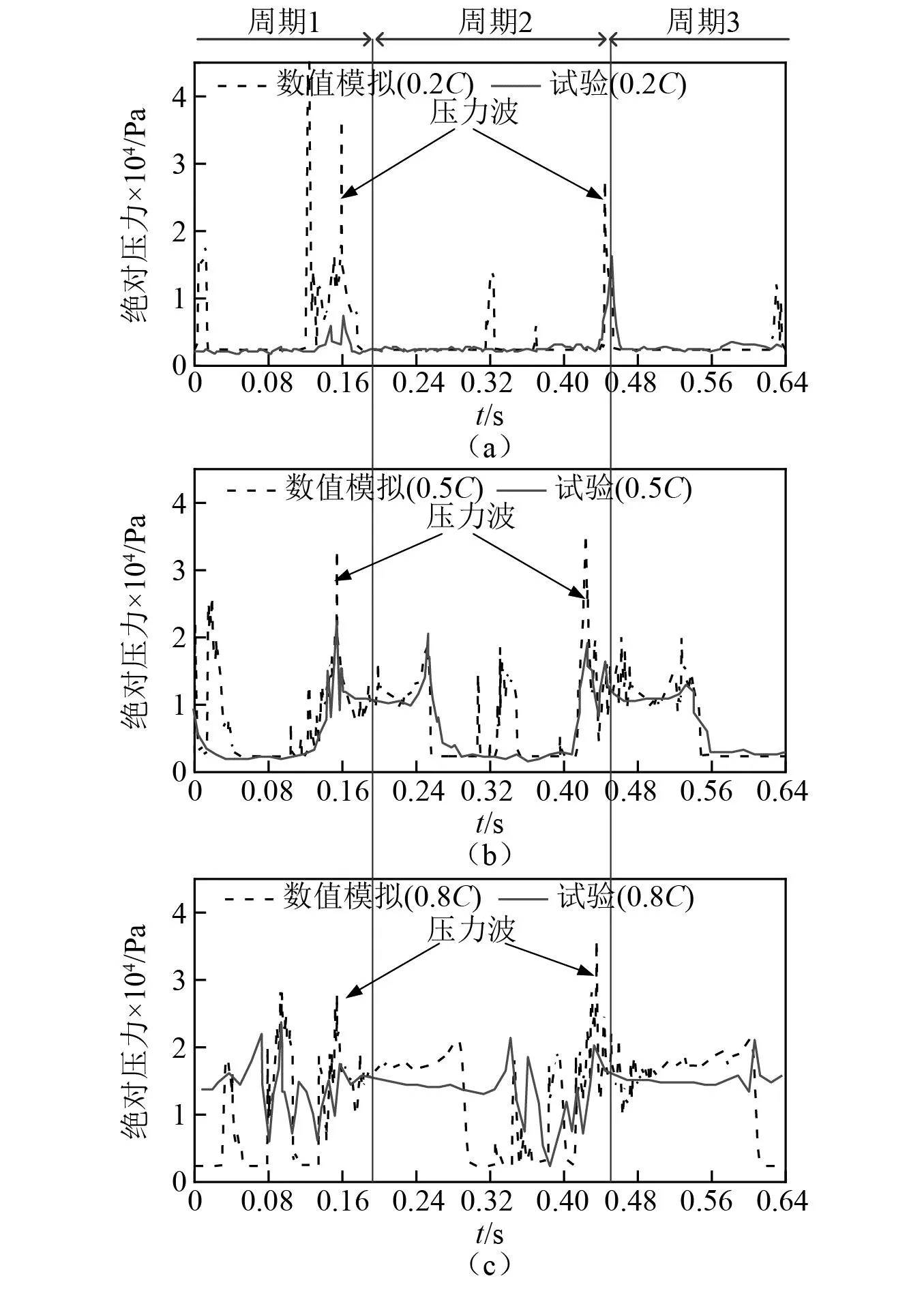
图6 水翼表面0.2C,0.5C和0.8C位置处的瞬态压力波动Fig.6 Instantaneous pressure fluctuations at 0.2C, 0.5C and 0.8C on the hydrofoil surface

2.2 非定常涡旋结构演化过程分析

2.1节阐述了压力波的产生的原因和传播过程,瞬态空化动力学与涡旋结构的演化密切相关,为了进一步研究压力波的瞬态特征,本节重点关注涡旋结构的演化。Q准则是研究空化流场中涡旋的重要方法之一,它由Haller[31]提出,公式如下

(30)

式中:Q为速度梯度张量的第二不变量;Ω为涡量张量;S为应变率张量。它反映了流体旋转和变形的相对强度。

图7通过涡量云图与Q判据的方法来对空化流动产生的涡旋进行示踪,展示了一个完整周期下的涡旋演变过程。由图7可知,空化行为对水翼周围和尾流的涡旋结构有很大影响,由于空泡的生长和脱落过程,涡旋结构随时间而变化,近壁面的涡量绝对值较大,这是由于近壁面的流动存在强烈的剪切效应所导致的。在t0+0/8T～t0+2/8T时,水翼吸力面的平滑涡旋结构随着片状空泡的发展而增长,在片状空泡末端开始出现不稳定波动附近。水翼尾缘附近仍能观察到由于上个周期脱落的云空泡而产生的涡旋结构。在t0+3/8T～t0+4/8T时,回射流推进的位置存在高涡量值,引起空泡内的扰动,增强湍流波动并且回射流会导致涡旋结构向上抬起,这说明回射流冲击了片状空泡的表面,最终导致云空泡脱落,云空泡向水翼下游移动时会产生大规模旋涡,云空泡内的涡量特征变得更加复杂。在t0+5/8T～t0+6/8T时,与回射流的弱冲击相比,云空泡溃灭产生的高压压力波会强烈扰乱涡旋的运动,水翼表面上的稳定涡旋结构被小尺度涡旋结构替代。这说明压力波的传播特性与空化涡旋结构及其演化存在密切关系。

图7 一个典型周期下的连续瞬时流场Fig.7 Continuous instantaneous flow field under a typical period

图8显示了压力波传播过程的Z方向上的均质化涡量特征。由于水翼表面的切向流的剪切作用,跨度方向(Z方向)上的涡量值远大于其他两个方向,所以本文只讨论Z方向上的涡量特征。水翼的上下方Z方向上的涡量的正负是不同的,正负值会在水翼尾部相互融合。当云空泡溃灭产生压力波时,由于压力波的冲击,Z方向上的涡量的稳定状态发生改变,出现了强烈的波动。波动会沿着水翼向上游移动,这与压力波的传播过程相对应。

图8 压力波传播过程的Z方向上的均质化涡量特征Fig.8 The homogenization vorticity characteristics in the Z direction of pressure wave propagation

图9显示了水体积分数等值面(αl=0.8)上的Q值分布和水翼表面的压力分布。当Q>0时,它表示该区域旋转效应大于剪切效应。当Q<0时,它表示该区域剪切效应大于旋转效应。在初始阶段(t0+0/8T～t0+2/8T),水翼前缘的Q值为负,而在附着的片状空泡的下游则为正。该结果表明旋转效应在片状空泡分离区域中占主导地位。在t0+3/8T～t0+4/8T的阶段,回射流导致的靠近壁面的空泡内出现更多的正Q值。当片状空泡生长到水翼后缘时,正Q值的区域出现在水翼的下游。

同时,附着的片状空泡出现更多负Q值区域,剪切效应变得更加显著。当云空泡进行向下游的翻转运动时,云空泡的表面上正Q值和负Q值区域交替出现。在t0+5/8T～t0+6/8T时,空化流场变得非常不稳定,Q值分布变得复杂。观察水翼表面的压力特征,压力波的传递的位置对应着水翼上的高压力位置。此时,正Q值区域显著,这说明压力波传递主要影响空化流的旋转效应。因此旋转效应和剪切效应共同主导了绕水翼非定常空化的流动过程。

2.3 基于动力学模态分解方法的流场分析

空化的非定常性会产生更加复杂的流场结构。DMD方法能够提取流场中的相干结构,揭示湍流空化流动的机理。本文工作一共模拟了48 000个时间步长,总时间为1.2 s,选择空化的最后3个脱落周期进行DMD分析。模态分解是基于中截面(Z=0)处的流场中各点水蒸气体积分数和X方向的速度进行的,每隔0.1 ms记录一次数据,速度场主要在X方向波动,这意味着速度X方向的分量数据对于模态分解更加稳定和稳健。

对提取出的样本进行DMD分解,可以获得复平面上的特征值。图10为DMD特征值的实部和虚部在单位圆上的分布,其中x轴代表实部,y轴代表虚部,由图10可知,两个实部相等,特征值总是关于实轴对称的,虚部互为相反数,这说明特征值是共轭的结果。特征值点与单位圆之间的关系揭示了相应模式的不稳定特性,如果一个特征值在圆外,这个特征值可能是不稳定的,这在周期流中是不可能发生的。由图10可知,大部分点位于单位圆内,说明该流动条件下的空化流动是准周期性的。

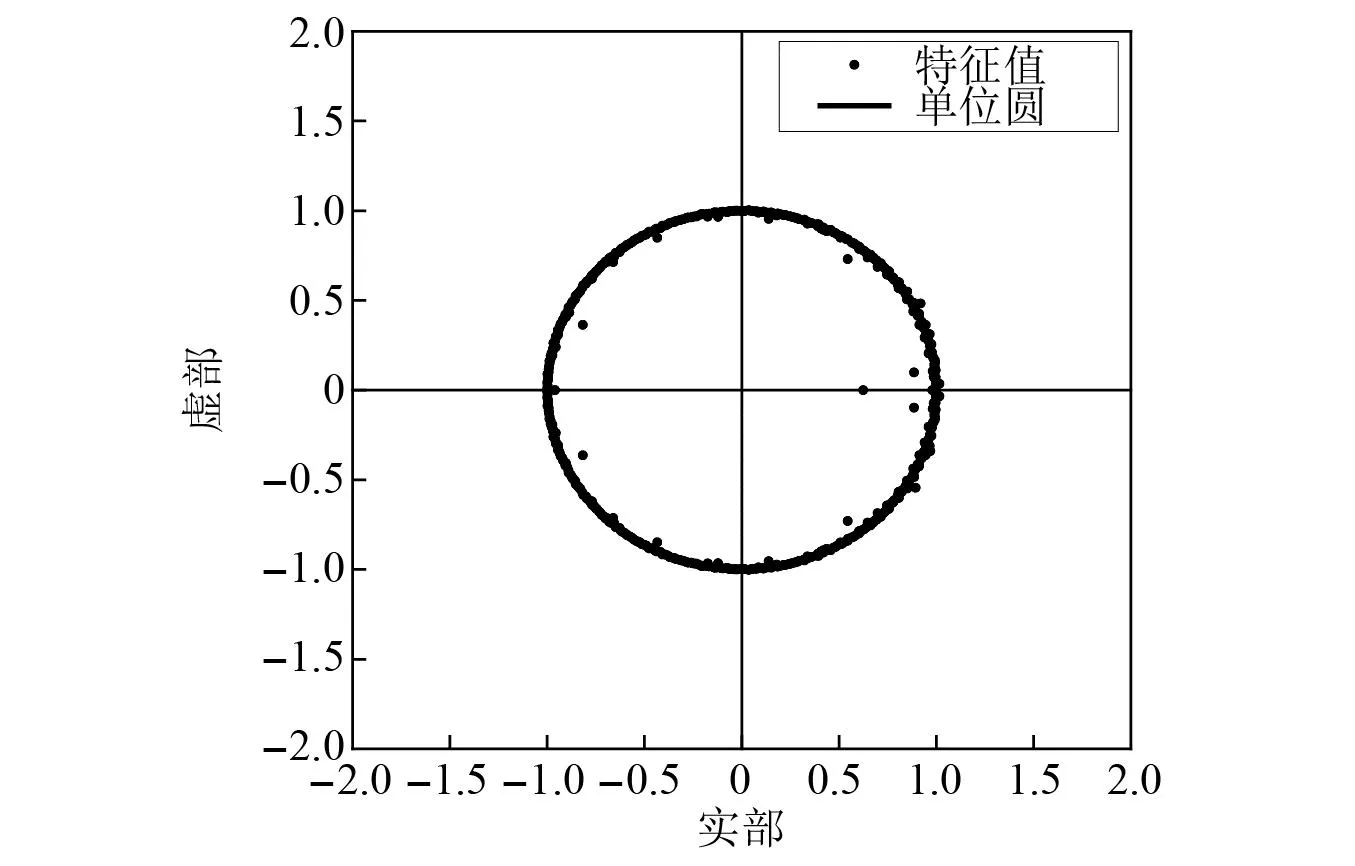
图10 复平面上模态特征值的分布Fig.10 Eigenvalue distribution on complex plane

一般情况下,DMD模态根据初始振幅进行排序,有时也可以根据频率或增长率进行排序。基于振幅的模态选择并不完善,因为流场中可能存在初始振幅很高但阻尼很大的模态。基于频率或增长率的模态选择是不完善的,因为这需要先验的物理知识。如果事先知道流场中必不可少的模态,自然有可能将他们纳入模型中,但该过程缺乏公平性。为了避免这种困难,采用能量高低来评价模态在流场中的主导作用。模态中的能量高低可由模态φi的范数表示

(31)

DMD分解后的特征值和各阶模态所含的能量大小相关。图11为不同阶模态的能量比率,不同阶模态的能量比率等于该阶模态能量占总能量的百分比。前4阶模态的能量在整个模态能量的分布中的占比是较大的,能够达到总能量的60%以上,其余模态的能量比率较低,这说明低阶模态可以表征为流场的主要信息。因此,选择前4阶DMD模态来描述流场。

图11 不同阶模态的能量比率Fig.11 Energy radio of different modes

图12为频率与能量的对应关系,模态1的频率为0,模态1在所有DMD模态中所占的能量比例最大,这表明模态1描述了空化流动的显著特征,代表了平均的流场状态。模态1不包含完整的流场信息而包含了流场中具有显著特征的流场信息。模态2的频率3.75 Hz,与空泡周期性脱落的频率一致,因此模态2可以表征空泡形态周期性演化的规律。模态3与模态4表示了更细微的流动模式,频率分别为7.51 Hz和11.27 Hz,分别为脱落频率的2倍和3倍。因此不同模态特征代表着流场的不同特性。

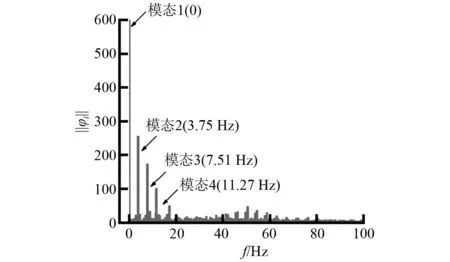
图12 模态与能量的对应关系Fig.12 Correspondence between modes and amplitude

为了明确前4阶模态对流场的重构效果,图13显示了重构后的X方向速度场和原始X方向速度场的比较。模态值忽略了虚部,只取实部模态进行分析。前4阶模态的重构可以很好地还原空化流动的主要特征,并且恢复了大部分流场信息。云空泡内部以及水翼后方的流动细节被忽略,这些区域的运动能量较小,运动形式复杂,因此是流场重构误差的主要来源。

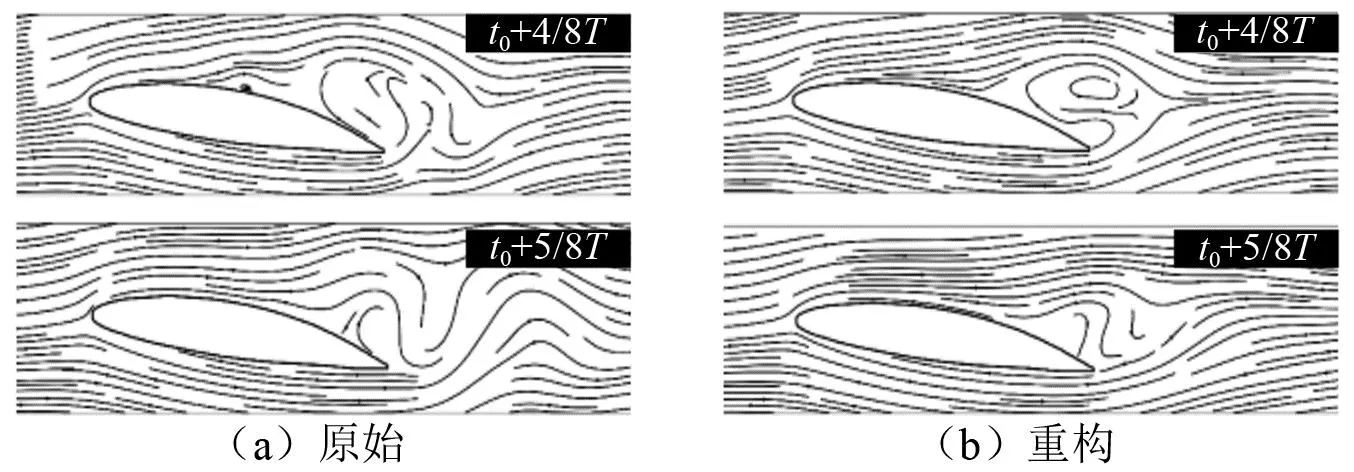
图13 重构X方向的速度场和原始X方向的速度场Fig.13 Reconstructed velocity field and originally simulated velocity field in X direction

表2为前4阶DMD模态的频率以及相应的放大率,DMD方法下的不同模态代表着不同的特征频率,为一一对应关系。每阶模态的放大率极小,这说明数值计算的误差极小,得到的结果具有极高的稳定性而且十分准确。

表2 DMD的各阶模态频率和放大率Tab.2 The frequency and magnification of each mode of DMD

图14展示了流场中不同变量进行模态分解后提取的前4阶模态,依据空化演化过程的主要特征可以将流场的相干结构分为两种:代表附着形片状空泡的附着结构和代表脱落云空泡的脱落结构,其中脱落云空泡是压力波产生的原因,可以代表压力波在流场中的能量贡献。1阶模态为静态模态,反映了平均的流场状态,它不随时间的变化而改变,代表了流场的基本骨架和主要特征。观察1阶X方向速度模态,在大多数区域值均为正值,水翼前缘上方出现最大值,在水翼的空泡影响区域为负值;观察1阶水蒸气模态,主要存在水翼表面以及水翼尾部的上方。水翼上方的主要正值区域与稳定平滑的片状空泡区域相对应,水翼尾部的负值区域代表了云空泡的脱落产生区域,这说明压力波效应和附着片空泡的演变占据了流场的主要能量。2阶模态捕获了空化周期性脱落的显著特征。观察2阶X方向速度模态,相干结构的分布有明显的正负区,水翼尾部的脱落结构向下游延伸,这代表了涡旋交替脱落的现象;观察2阶水蒸气模态,水翼上方正值与负值交替的相干结构特征表示云空泡产生后随着时间推移向下游移动的过程。3阶和4阶模态为具有较低的能量的高阶模态,代表了空化流的复杂性和小尺度结构的能量轨迹,并且相干结构的分布随着频率的增加而变得更加分散。观察高阶的X方向速度模态,随着模态阶数增高,其所含能量逐渐减小,脱落频率逐渐增大,涡旋数量也在增多,尤其体现在水翼上方的相干结构数量逐渐增多。3阶模态的相干结构分布是基本对称的,但是更高阶模态下的空化三维效应更加凸显,这导致4阶模态中的相干结构是不对称的。观察高阶水蒸气模态,在大多数区域,尤其是在远离水翼面的区域中,该值为0。相干结构的分布仅出现在水翼的吸力侧,并且是正值和负值交替出现,而在水翼的另一侧则为0,这表明水蒸气的模态特性与空泡的演化息息相关。水翼的尾部区域是云空泡产生和溃灭的位置,复杂空泡演化过程导致水蒸气的相干结构的分布更加分散。

图14 DMD的前4阶动力学模态Fig.14 The first 4 dynamic modes of DMD

3 结 论

本文基于可压缩流假设与均相流假设,采用分离涡模拟的方法对非定常空化流动进行了求解。分析了压力波的产生与传播过程、压力波的性质以及压力波传播对涡旋结构的影响,得到的结论如下:

(1) 脱落的大尺度云空泡溃灭是压力波产生原因,压力波的传递过程会导致片状空泡的收缩,而且在水翼表面产生瞬态的高压力脉冲。跨越压力波面前后的水蒸气含量与速度方向存在着跃变现象。

(2) 压力波会强烈扰乱涡旋的运动,水翼表面上的稳定涡旋结构被卷起,并且被小尺度涡旋结构所替代,稳定的Z方向涡量出现了强烈的波动,波动随着压力波沿着水翼向上游移动。压力波传递主要影响空化流的旋转效应。

(3) 利用DMD方法对流场模态分解,1阶模态的频率为0,代表了流场的基本骨架和主要特征。压力波效应和附着片空泡的演变占据了流场的主要能量。2阶模态的频率与空泡脱落的频率一致,代表了空化周期性演化的特性。水翼上方正值与负值交替的相干结构特征表示云空泡产生后随着时间推移向下游移动的过程。3阶模态与4阶模态的频率分别为脱落频率的2倍和3倍,代表了空化流的复杂性和小尺度结构的能量轨迹,并且相干结构的分布随着频率的增加而变得更加分散。