基于响应面法和MOGA 的重载曲轴形貌优化研究

马文生，龚钞，李方忠，刘春川

（1.重庆理工大学机械工程学院，重庆 400054；2.重庆水泵厂有限责任公司国家企业技术中心，重庆 400033；3.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨 150006）

0 前言

大型隔膜泵主要用于石油、化工、采矿等领域，在高磨蚀、高浓度固液两相介质长距离管道化输送领域占据绝对优势地位［1-2］。其中重载曲轴作为大型隔膜泵动力端的关键零部件，承受着由活塞端带来的连杆力、支撑轴颈处的摩擦力以及自身旋转惯性力等引起的周期性载荷。因此，研究曲轴的强度、刚度等很有必要。

近年来，针对曲轴的优化，国内外学者进行了大量的相关研究。游孟平等［3］通过建立曲轴的刚柔耦合动力学模型进行动力学仿真，研究曲轴表面粗糙度对疲劳安全系数及疲劳寿命的影响，结果表明：曲轴表面粗糙度越大，曲轴的疲劳寿命越短。刘洁、卢秋霞［4］通过静强度分析及模态分析对六缸发动机曲轴结构进行优化，最终降低曲轴质量12.7%。ALIAKBARI 等［5-6］、LI 等［7］对曲轴疲劳强度进行分析，发现曲轴的疲劳强度不足的原因是圆角处表面容易产生疲劳裂纹。因此，对曲轴圆角表面进行硬化处理能大大减少疲劳裂纹的产生。杨秀琴［8］为解决某型号曲轴在辊锻制坯阶段模具磨损严重导致成形时出现折叠的现象，选取过渡圆角、入模圆角、过渡斜度3个关键参数，以降低磨损量为目标，基于正交试验进行模具结构优化研究，有效减少了曲轴成形时出现折叠的现象。丛建臣等［9］通过对内燃机曲轴进行扭转疲劳试验研究，发现连杆颈油孔是扭转疲劳失效最常见部位，通过轴颈表面感应淬火处理降低曲轴的扭转疲劳强度约30%，通过抛磨油孔内壁提高曲轴的扭转疲劳强度25%以上。

对于重载曲轴而言，其整体应力大小通常远小于材料的强度极限，其失效往往是因为曲柄间过渡圆角处的疲劳破坏。因此，降低过渡圆角处的最大应力值可以有效提高重载曲轴的寿命。CHEN等［10］、WANG 等［11］发现圆角半径对曲轴的强 度影响较大，随着圆角半径的减小，其应力值会显著增大。因此，本文作者以重泵公司某型号隔膜泵曲轴为研究对象，以ANSYS 为研究工具，研究曲轴圆角处的结构参数对圆角上的最大应力值及曲轴整体变形量的影响。采用Kriging 插值法得到优化目标P3（轴颈与曲柄过渡圆角的最大应力值）、P4（曲柄斜面处圆角的最大应力值）、P5（曲轴的最大变形量）与设计变量P1（曲柄臂斜面倾斜角）、P2（斜面处圆角半径）之间的具体函数关系，在支持曲轴模型生成的最大尺寸范围内，应用多目标遗传算法寻找最优的结构参数。

1 参数化建模

参数化建模在形貌优化设计过程中很常见，它通过改变参数变量自动更新产品的结构［12］。本文作者基于UG 建立曲轴圆角处的局部参数化模型，见图1。如图2 所示，变量P1、P2为圆角处结构特征参数，决定了曲柄处的形状样貌。在建模过程中，除了安装工艺孔和油孔外，其他几何特征均未做简化，特别是计算所关心的各个圆角处。为方便后续表述，将曲拐从扭矩输入端开始依次编号为拐1、拐2、拐3。

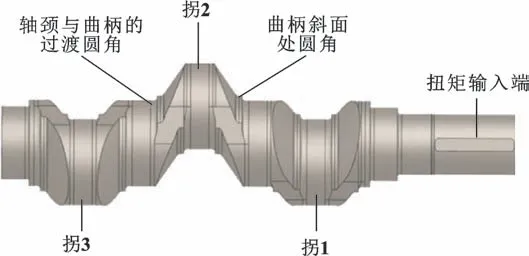
图1 曲轴的三维模型Fig.1 3D model of crankshaft

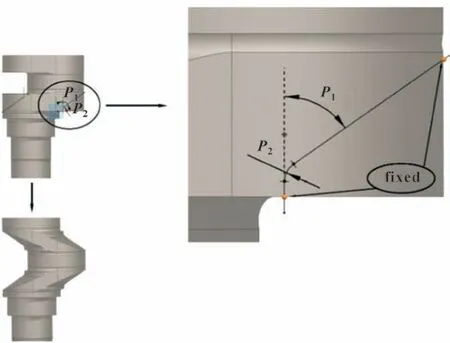
图2 曲柄参数化结构Fig.2 Crank parametric structure

2 静强度计算

本文作者采用静强度应力分析方法来确定曲轴的危险工况及应力分布情况。为获取更加精确的曲轴交变应力水平，综合考虑计算精度和计算时间因素，将曲轴一个旋转周期内的受力情况划为72 个载荷工况。当曲柄转角θ＝0°时，曲轴受力情况为第一载荷工况。当曲柄转角θ＝5°时，曲轴受力情况为第二载荷工况，以此类推。

2.1 曲轴参数

文中研究对象为三拐四支撑结构曲轴，各曲拐之间相隔120°，曲轴三维结构模型见图1。曲轴材料参数及曲轴-连杆机构部分参数如表1 所示。

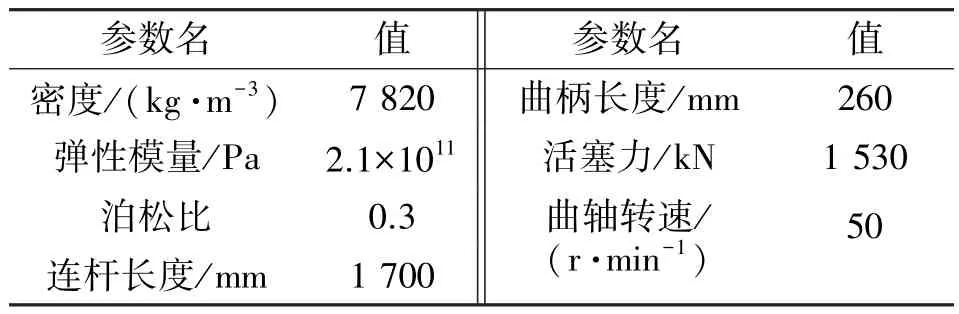
表1 曲轴参数（部分）Tab.1 Crankshaft parameters（partial）

2.2 载荷分析

隔膜泵工作时，作用在曲轴上的力有：经连杆传递到曲轴的连杆力、曲轴与支撑轴承间的摩擦力、曲轴自身的旋转惯性力。通过设置摩擦接触的方式添加曲轴与支撑轴承间的摩擦力，通过添加初始旋转速度来考虑旋转惯性力对曲轴的影响，而连杆力则通过推导计算得到具体数值。

曲轴-十字头系统的机构运动简图及受力见图3。θ为曲轴曲拐与x轴夹角，当曲拐转角θ＝0～180°时，对应工作行程，十字头所受活塞力F＝1 530 kN；当曲拐转角θ＝180°～360°时，对应非工作行程，根据文献［13］可以将十字头所受活塞力近似看为F＝0 kN。

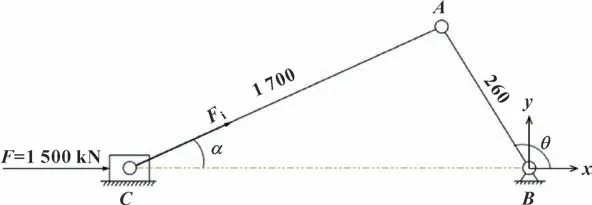
图3 曲轴-十字头系统的机构运动简图Fig.3 Schematic of mechanism movement of crankshaftcrosshead system

在工作行程时，根据正弦定理可以得到

则作用于曲轴上的连杆力Fi可表示为

式中：θ为曲拐转角，（°）；F为活塞力，F＝1 530 kN；AB为曲拐到轴旋转中心距离，AB＝260 mm；AC为连杆长度，AC＝1 700 mm。根据上述公式，可得到不同曲拐转角θ下的连杆力Fi的具体数值。需要注意的是，在静强度计算过程中，曲轴某一工况位置上的载荷情况应为该工况下3 个曲拐受力情况的叠加状态。

2.3 边界条件

在支撑轴颈处增加轴套来模拟轴承与曲轴之间的摩擦影响，在轴套与曲轴之间添加摩擦因数为0.12的摩擦接触，并设置接触间隙为0.25 mm。此外，如图4 所示，约束曲轴键槽侧面的z向旋转自由度；约束两端支撑轴套的径向跳动（即x、y方向上的位移）；约束另外两个支撑轴套表面的径向和轴向跳动（即x、y、z方向上的位移）；约束曲轴底端面的轴向跳动（即z方向上的位移）。

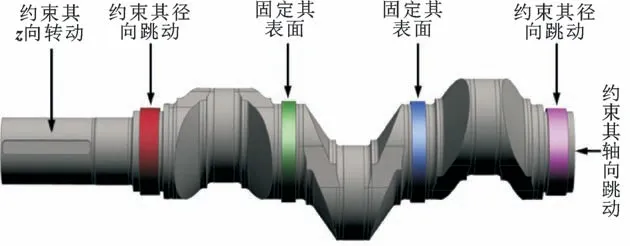
图4 曲轴静强度计算的边界条件Fig.4 Boundary conditions for static strength calculation of crankshaft

2.4 网格划分

为了兼顾强度计算的准确性和计算时间，应在批量计算之前，对计算模型的网格进行无关性验证。由于曲轴形状的不规则，仿真过程中采用四面体网格划分法对曲轴整体进行体网格划分，细化各过渡圆角表面上的面网格。

如表2 所示，经过多次试验，当网格尺寸由体网格为20 mm、面网格为5 mm 转变为体网格为10 mm、面网格为5 mm 时，P3和P4值的变化几乎忽略不计。因此，确定以曲轴体网格大小20 mm、圆角处面网格5 mm 作为后续计算时的网格尺寸。此时，模型包括1 925 088 个节点、1 313 433 个单元，如图5 所示。

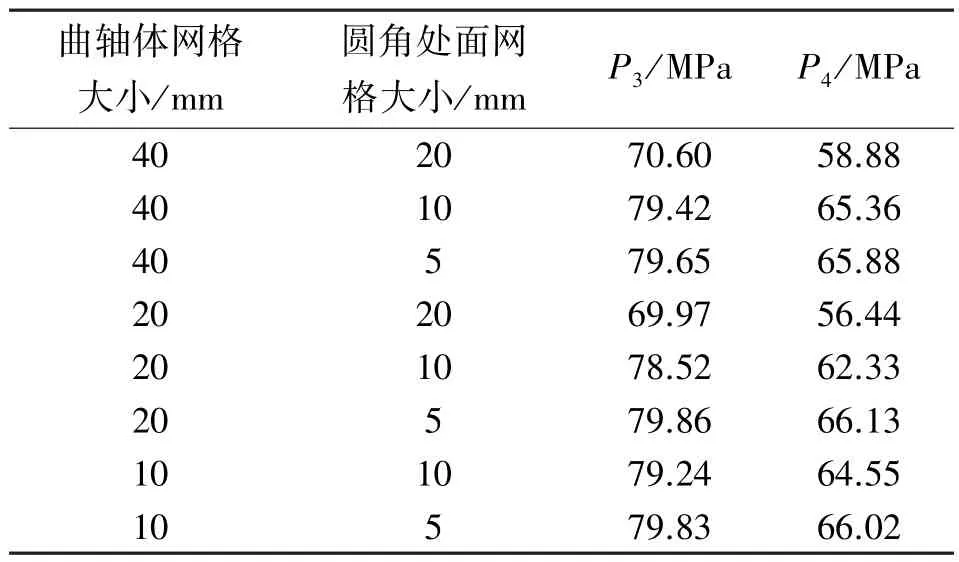
表2 网格无关性验证试验数据Tab.2 Grid independence verification test data

图5 曲轴整体网格Fig.5 The grid of crankshaft

2.5 计算结果

在solver 中将载荷步增至72 个，每个载荷步代表一个曲轴工况，将前面计算得到的72 个工况下的连杆力分解到x、y轴方向上，并以bear loading［14］的方式依次施加到对应曲拐上，实现对72 个工况进行批量计算。经验证，此方法与单独计算各个工况所得结果一致。

图6 展示了72 个工况下的各圆角处最大应力值。其中，P3的最大值出现在第25 个工况下，为80.79 MPa。此时拐1 曲柄转角为0°，所受连杆力为1 530 kN；拐2 曲柄转角为120°，所受连杆力为1 543.6 kN；拐3 曲柄转角为240°，所受连杆力为0 kN。而P4的最大值出现在第13 个工况下，为66.50 MPa。此时拐1 曲柄转角为300°，所受连杆力为0 kN；拐2曲柄转角为60°，所受连杆力为1 543.6 kN；拐3 曲柄转角为180°，所受连杆力为1 530 kN。

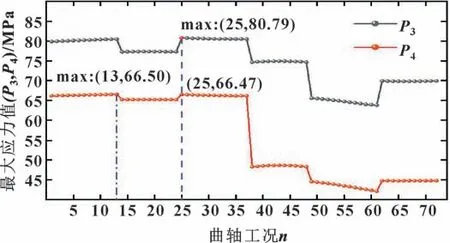
图6 曲轴在72 个工况下的圆角处最大应力值Fig.6 Maximum stress of crankshaft at fillet under 72 working conditions

很显然，曲轴的整体受力大小在第13 工况和第25 工况下一样。但拐1 和拐3 受力情况发生交换，而拐2 没有变化。考虑到P3在所有工况下均大于P4，且P4在第13 工况下和第25 工况下的最大值相差不大，仅为0.03 MPa。因此，确定第25 工况作为后续曲柄形貌优化的计算工况。第25 工况下的曲轴圆角处等效应力云图如图7 所示。

3 曲柄形貌优化

串联UG 和Workbench 的数据接口，结合Design Exploration 模块搭建曲柄形貌优化的计算环境。

图8 所示为整个优化过程的流程。首先，建立参数集，其中包含设计变量和优化目标。确定设计变量的约束范围，在约束范围内均匀地设计试验方案，并计算得到不同方案下的计算结果。然后，基于计算结果构建各目标关于变量的响应面，并通过多目标遗传算法在约束条件下寻找目标的最优值。最后，将最优结果对应的设计变量返回到几何模型中进行计算，得到仿真结果。如果仿真结果与优化结果之间的误差较小，说明优化成功，并选取一个最优候选点，对其取整作为优化最终结果。否则，重新构建各响应面，并再次寻优、验证。

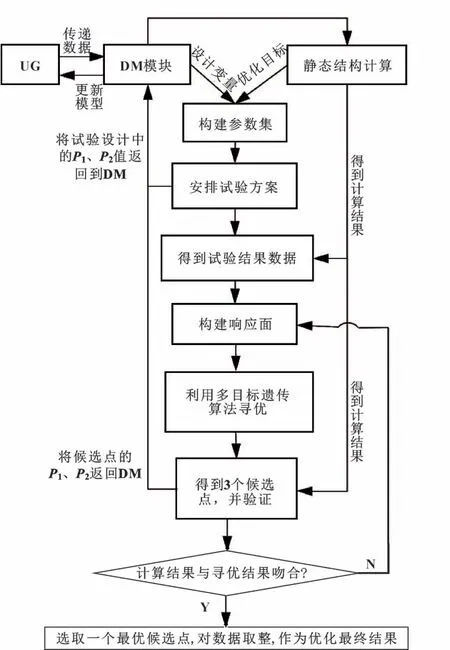
图8 曲柄形貌优化流程Fig.8 Flow of crank shape optimization

3.1 构建响应面模型

响应面模型是利用合理的试验设计方法并通过得到对应的试验数据，采用插值或者拟合的方法来构建变量与目标之间的数学函数关系。它可以清晰地表现出各变量对目标的影响关系，便于寻找最优目标。响应面的构建包括试验设计和模型构建这两部分［15］。

3.1.1 试验设计

通过设计一系列的试验方案，运用尽量少的资源和计算时间，获得可反映设计变量与优化目标的高度相关信息数据。试验设计中，好的试验方案，既能降低计算成本又能提高响应面精度［16］。根据第3.2 节中的不等式（9）（10），P2的取值范围会随着P1的变化而变化，为了更加均匀地设计试验样本点，将P1设置为6 水平因素，P2为多水平因素，一共31 组试验样本点。

部分试验方案及结果见表3，图9 给出了P1处于不同水平下，曲轴最危险工况下各优化目标随P2变化的规律曲线。

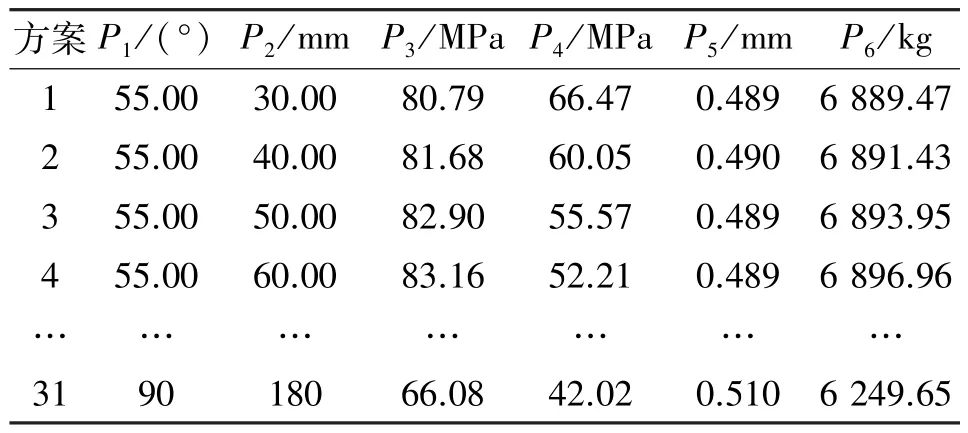
表3 部分试验方案及结果Tab.3 Partial test scheme and results

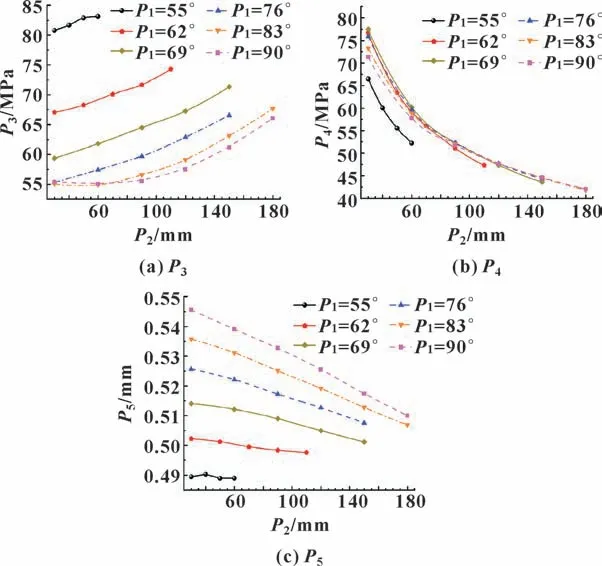
图9 各优化目标随P1、P2变化的规律曲线Fig.9 Regularity curves of optimization objectives changing with P1 and P2：（a） P3；（b） P4；（c） P5

从图9 可以看出：在P1不变的情况下，优化目标P3随着P2的增大而增大，而P4和P5则随P2的增大而减小。其中，P4的下降趋势远大于P5。对P4来讲，P2即其对应处的圆角半径是影响其大小的主要因素，这与文献［10-11］的结论一致。此外，当P1＞55°之后，它对P4的影响将变得很小；而P3、P5受P1的变化影响却十分明显。因此，想要通过直接观察计算结果找出最优的设计变量是不可能的，需要通过构建响应面模型来精确表达设计变量与优化目标之间的数学函数关系，并应用优化算法来寻找最优解。

3.1.2 基于Kriging 法构建响应面模型

Kriging 法是一种元建模算法，可提供改进的响应质量并拟合输出参数的更高阶变化。它是一种精确的多维插值，可以插值试验设计样本点，结合了类似于标准响应曲面的多项式模型（提供设计空间的“全局” 模型）加上局部偏差，其表达式为

其中：y（x）是待拟合的响应函数；β是基函数回归系数；f（x）是变量x的多项式响应面模型，提供设计空间的全局近似模型；z（x）是期望为0、方差为σ2的高斯随机函数。其协方差矩阵为

式中：R为相关矩阵。选择高斯相关函数为

式中：θk是相关函数参数，用于衡量两样本点之间的相关性随两点间的距离增加的衰减度，相关性越小，生成的响应面越光滑；xi，k和xj，k分别是样本点xi和xj的第k个元素。

基于上述Kriging 响应面模型理论以及前面得到的试验设计样本点，建立Kriging 响应面，得到设计变量对优化目标的响应面模型，如图10 所示。其中各响应面模型的均方根误差分别为2.044 9×10-7、2.326×10-6、2.538 2×10-11，这表示响应面拟合效果良好。

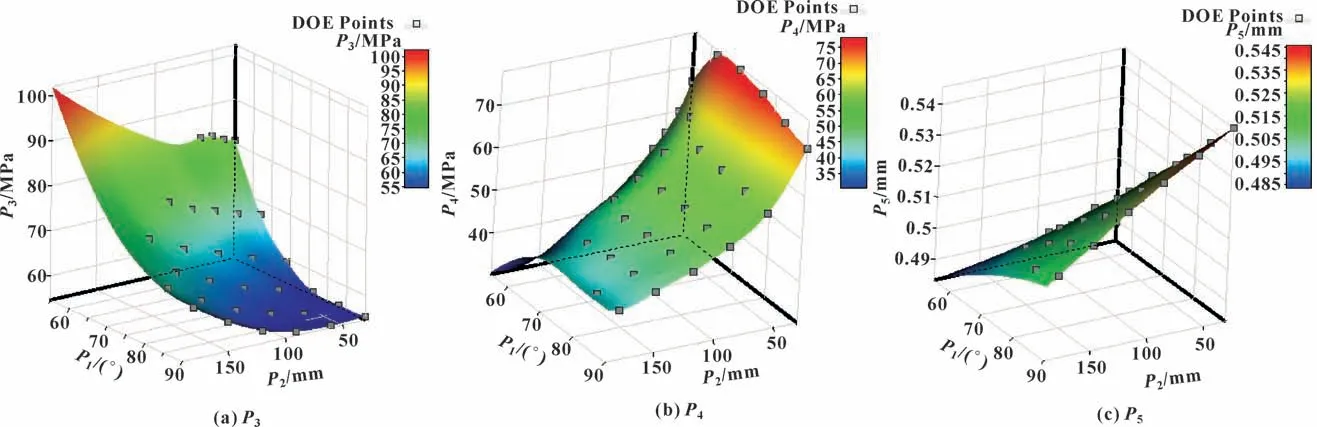
图10 各优化目标的响应面模型Fig.10 Response surface models of each optimization objective：（a） P3；（b） P4；（c） P5

3.2 多目标遗传算法寻优

MOGA（Multi-objective Genetic Algorithm）是当前应用较为广泛的多目标优化算法之一，相比较其他优化算法，其算法复杂性低、解集的收敛性好、运行速度快。MOGA 赋予多个目标函数不同的权重并将它们组合成一个标量适应度函数。与单目标遗传算法不同的是，MOGA 中多个目标函数的权重不是恒定的，而是随机指定的。因此，MOGA 的搜索方向是不固定的，如图11 所示。当多目标优化问题具有凹Pareto前沿时，恒定权重的单目标遗传算法往往无法找到整个Pareto 前沿［17］（即所有Pareto 最优解）。因此，作者采用多目标遗传算法寻找最优解。

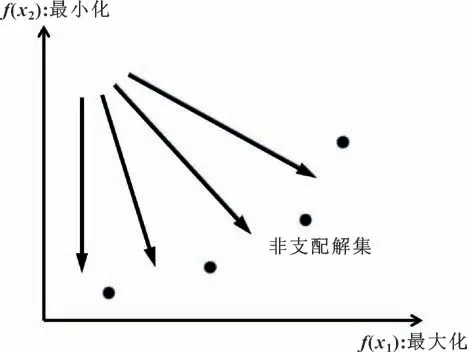
图11 多目标遗传算法的寻优方向Fig.11 Optimization direction of multi-objective genetic algorithm

3.2.1 建立多目标优化模型

进行多目标优化需要先确定此次优化的设计变量、目标函数和约束条件，以建立优化模型。本文作者以P1、P2作为设计变量，以P3、P4、P5作为优化目标，以P1、P2的尺寸约束范围作为约束条件，以响应面模型表达优化目标与设计变量之间的函数关系。优化模型用下面的形式表示：

式中：f（xi）为优 化目标；xi为设 计变量；xi、L、xi，U分别为设计变量xi的下限值和上限值；wi为各优化目标所占权重，表示对应目标对于整体优化的重要性。每个权重表示如下：

式中：rj为非负随机数。MOGA 中每次选择字符串的时候都会重新赋予新的不同权重值，以保证寻优方向的随机性。

如图12 所示，将曲柄外形轮廓之间的关系单独提取出来，此时的DE长度是P2的极限值。如果P2值超过极限值，UG 中将不能生成对应三维模型。

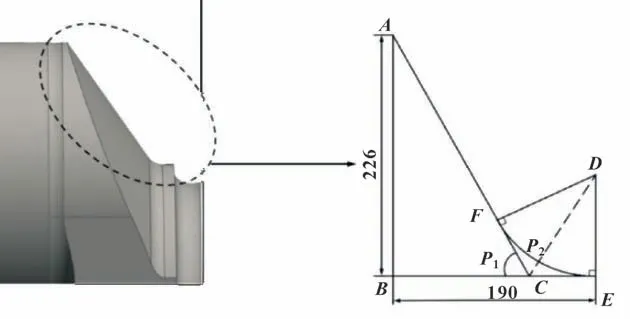
图12 P1、P2 之间的关系Fig.12 Relationship between P1 and P2

于是可以得到：

当P1＞90°后，曲柄明显向内凹陷，会导致结果刚度显著降低。因此P1的范围为

以式（9）和式（10）作为优化的约束条件，得到具体的优化模型为

式中：P3、P4、P5代表对应的响应面模型。

3.2.2 优化结果

设置初始样本数为2 000，每次迭代的样本数为400，允许Pareto 的最大百分比值为70%，收敛稳定性设置为2%。得到优化后的Pareto 前沿见及其对应的Pareto 解集见图13。

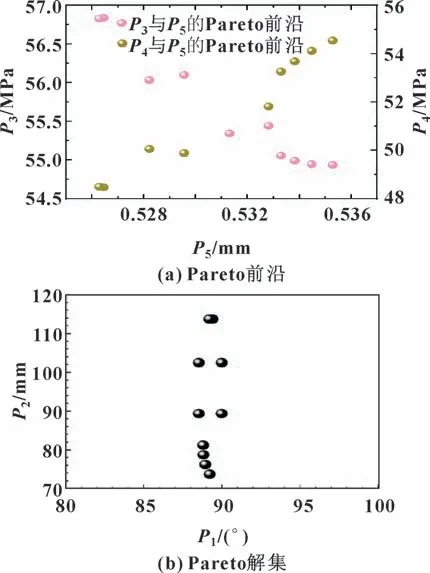
图13 优化结果Fig.13 Optimization results：（a）Pareto frontier；（b）solution set of Pareto

根据文献［18］可得曲轴的刚度条件为

式中：［y］为轴的允许挠度，mm；L为轴的跨度，L＝3 574 mm。

由式（13）可得曲轴允许的最大变形量为0.714 8 mm。对比Pareto 前沿可知，所有的非支配解都满足曲轴的最大变形量要求。从图13（b）可以发现，Pareto 解集中P1都接近于90°。针对这一发现，作者做出的合理解释是：虽然随着曲柄斜面倾斜角P1的增大，曲轴的最大变形量也将增大，但在满足曲轴刚度条件的情况下，曲轴的曲柄斜面倾斜角接近90°可能是一种能够最大程度地降低曲柄斜面处圆角最大应力值和轴颈与曲柄过渡圆角处的最大应力值的极限状态。这将在后续研究中进一步验证。

选择P3＝54.94 MPa、P4＝54.55 MPa、P5＝0.535 mm 作为最终优化结果，此时，P1＝89.20°、P2＝73.71 mm。将结果圆整为P1＝90°、P2＝75 mm返回到几何模型中，得到仿真结果为P3＝54.89 MPa、P4＝54.31 MPa、P5＝0.535 mm，与优化结果几乎一致。最终结果与优化前相比，P3下降了32.06%，P4下降了18.29%，P5上升了9.41%，但仍满足刚度条件要求。仿真结果见图14，曲轴曲柄优化前、后对比见图15。

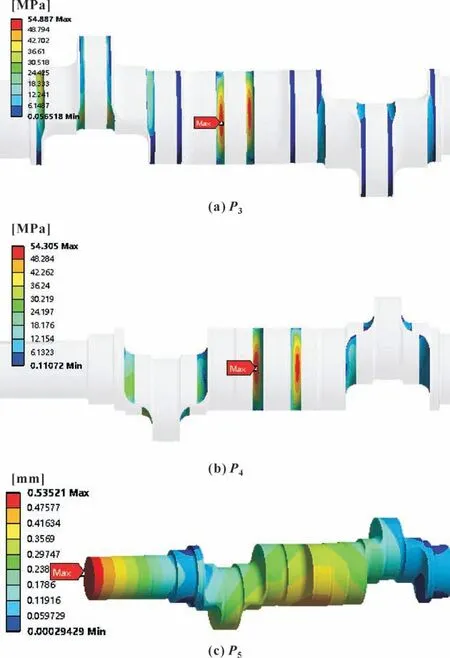
图14 仿真结果Fig.14 Simulation results：（a） P3；（b） P4；（c） P5

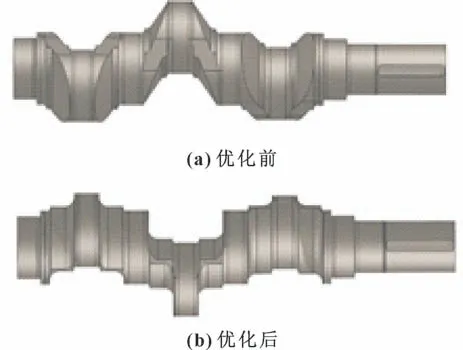
图15 曲轴曲柄优化前后对比Fig.15 Comparison of crankshaft crank before and after optimization：（a）before optimization；（b）after optimization

4 结论

本文作者从圆角处结构参数优化的角度出发，对曲轴进行形貌优化。首先，分析曲轴的受力情况，将曲轴运转过程分为72 个计算工况。采用静强度分析方法确定曲轴圆角处于最大应力值时的计算工况，并以此工况作为后续形貌优化的计算工况。随后，根据曲轴三维模型的生成条件确定合理的试验样本点，并得到各样本点的计算结果。利用响应面模型定量地表示设计变量P1、P2与优化目标P3、P4、P5之间的函数关系。最后，构建多目标优化模型，使用多目标遗传算法寻找P1、P2的非支配解集。可以得到以下结论：

（1）曲轴的危险工况为第25 个工况，此时曲轴圆角处的最大应力值为80.79 MPa。

（2）在P1不变的情况下，P2的增大会导致P3的增大，P4、P5的减小。其中，P4的减小趋势显然大于P5的减小趋势。

（3）对于P4来讲，其对应的圆角半径P1是影响其大小的主要因素，并且当曲柄斜面倾斜角大于55°之后，其对于P4的影响将逐渐变小；而P3、P5随P1的变化影响始终表现得较为明显。

（4）得到的Pareto 解集中P1都接近于90°。这可能是在满足曲轴刚度条件的情况下，P1接近90°能够最大程度地降低P3和P4的极限状态。

（5）确定最优结果P1＝90°、P2＝75 mm，此时P3＝54.89 MPa、下降了32.06%，P4＝54.31 MPa、下降了18.29%，P5＝0.535 mm、上升了9.41%（但仍满足要求）。