基于模糊PI 的CVT 用电动油泵控制研究

支金泽，安颖，高帅

（湖南科技大学机电工程学院，湖南湘潭 411201）

0 前言

目前，以内燃机为动力的乘用车用CVT（Continuously Variable Transmission）的液压油泵多采用发动机驱动的定量机械泵，CVT 控制、冷却润滑的流量压力需求与油泵供油量之间存在“需求矛盾”，这种矛盾迫使油泵设计者需充分考虑油泵低转速、CVT高流量需求的极限工况（例如，紧急制动工况和急加速工况），因此导致了CVT 油泵在正常行驶工况下的流量冗余、压力冗余（溢流损失）及能耗增加。VAN DER SLUIS 等［1］研究表明，在NEDC 循环工况下，在发动机输入CVT 的总功率中，液压油泵的功率损失占比达到12%。

CVT 的流量需求分为两部分：作动器所需要的高压力部分，用于钢带夹紧；润滑冷却所需的低压力部分，用于变矩器液力传动、部件润滑及系统散热，这部分低压流量需求仅需0.8 MPa 以内的压力即可满足。而上述传统CVT 则充分兼顾极限工况将全部流量需求按照最高压力需求供油。

为降低油泵的能量损耗，必须要降低溢流损失以实现按需供油，并随着车辆的混动化，采用可控电动油泵作为CVT 供油源，实现发动机转速与油泵供油流量的完全解耦是可采用方式之一［2-3］。在此种方案下，仅需通过改变油泵电机在CVT 不同运行工况下的转速来满足CVT 流量需求，而油压也可在电机能力范围内实现自动适应。由于永磁同步电机（Permanent Magnet Synchronization Motor，PMSM）具有体积小、可靠性高、能量密度高、能量转换效率高等优点［4］，因此文中电动油泵选取永磁同步电机作为驱动，并进一步深入研究PMSM 的控制策略。

目前，许多研究人员和学者已经提出了多种PMSM 的控制策略。传统PID 控制策略因易于实现且对硬件运算能力需求较小而得到了广泛的应用，但是由于定参数对环境、工况的适应力较差，无法在全工况范围内实现良好的动静态调控特性［5-7］；模型预测控制依赖于模型精度，尽管对于复杂时变非线性系统的控制具有较大优势，但该方法对模型参数变化较为敏感［8-9］；最大转矩比电流控制通常以查表法实现，但由于数据量较大，系统的响应速度会受到严重影响［10-12］。邹浙湘等［13］利用数学拟合以解耦控制电流分量，采用此方法的MTPA 控制算法对比查表法虽然提高了系统的响应速度，但仍具有很高的运算复杂程度。智能控制算法在永磁同步电机上的应用也相继被提出：胡达等人［14］采用基于神经网络的滑模控制，利用神经网络的自主学习训练在线调整滑模面的阶次，有效提高了动态跟踪性能并减小了稳态误差，但神经网络需要大量的训练集且需要长时间学习才能提高精度。姜伟、乔林等人［15-16］应用遗传算法于PMSM的控制系统中，利用遗传算法寻优控制参数，提高了控制系统的抗干扰能力，但容易收敛于局部最优解。欲确保全工况范围内PMSM 控制算法的控制品质，并为有效解决工程应用中的实时性与成本限制，陈文卓、刘宗锋等［17-18］将模糊控制算法用于控制电机，充分利用了模糊控制解决非线性复杂系统的能力，有效地提高了响应速度和稳定性。可见，模糊控制算法用于控制电机具有兼顾设计难度、硬件成本和控制品质的应用潜力。因此，本文作者拟采用模糊PID 控制方法实现CVT 电动油泵的控制，并深入研究控制品质。首先在构建永磁电机数学模型的基础上，加入了模糊PI 控制器，其次将CVT 油泵模块加入到模型中，并进一步地在CVT 的紧急制动工况下仿真验证了该控制算法的有效性和可行性。

1 PMSM 的数学模型

为了分析和求解PMSM 的数学模型，此处对电机做理想假设，即定子绕组感应电动势呈正弦波，忽略涡流和迟滞损耗、铁芯饱和效应［19］。

首先，为了实现电压与电流的解耦，需要利用坐标变换。Clarke 变换是静止坐标系变换，实现三相与两相之间的转换，亦称为3S／2S 变换，具体关系如图1 所示。

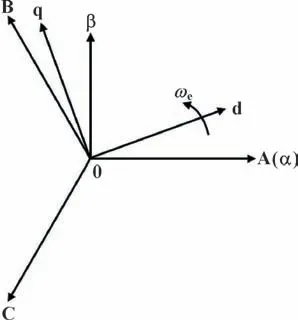
图1 三坐标系关系Fig.1 Relation of three coordinates

按照幅值不变的变换规则，变量之间关系为

则反Clarke 变换为

其中：iA、iB、iC是电机三相定子电流；iα、iβ是α-β 坐标系的定子电流，此处物理量也可用电压、磁链代替；T3s／2s为Clarke 变换矩阵，T2s／3s为反Clarke变换矩阵。

Park 变换是实现两相静止坐标系α-β 到两相同步旋转d-q 坐标系的转化，反之亦是反Park 变换。具体如下：

则反Park 变换为

同理：T2s／2r、T2r／2s分别为Park、反Park 矩阵。经过以上两种变换处理后，便可得到以下在d-q 坐标系下简化、解耦的电压方程：

磁链方程可表示为

电机电磁转矩方程为

式中：ud、uq、Ld、Lq、ψd、ψq分别为d-q 坐标系下定子电压、定子电感、定子磁链；Te为电磁转矩；Pn为电机极对数；ψf为转子永磁体产生的磁链；Rs为定子电阻；ωe为电角速度。

2 PMSM 矢量控制原理

2.1 矢量控制

矢量控制常用于解决交流电机的控制问题，其本质是解耦定子电流矢量，控制方式与他励型直流电机相似，极大地简化了电机的整个控制过程［5］。在电机的控制过程中，磁链和转矩的大小受控于两个电流分量，通过改变id、iq值的大小，便可完成电机转速与转矩的输出。文中采用id＝0 控制，则式（7）可化简为

该矢量控制基本结构如图2 所示。从图中可以看出其控制流程，控制系统实际电机转速n和目标转速nref的差值送入模糊PI 控制器，由于采用id＝0 矢量控制，便可得iqref，然后电流环PI 控制器计算目标值iqref与反馈值iq之差，便得到目标的直、交轴电压ud和uq，再经Park、Clarke 逆变换和空间矢量脉宽调制（SVPWM）后，产生间隔120°电位角的三相正弦交流电以驱动永磁同步电机。

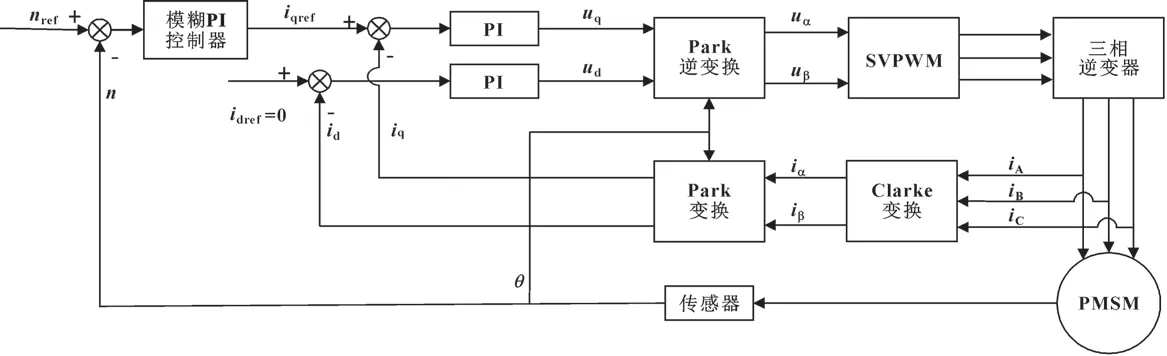
图2 永磁同步电机矢量控制结构框图Fig.2 Vector control structure block diagram of PMSM

2.2 空间矢量脉宽调制（SVPWM）

在电机调速过程中，其目标是产生一个理想的、标准的圆形旋转磁场，从而带动转子转动实现调速，而SVPWM 的主要功能就是产生近似圆形的旋转磁场。SVPWM 技术的原理是利用特定的组合和序列信号来关断和导通功率开关器件，使之产生三相正弦电压作用于电机定子，以得到圆形旋转磁场［20］。

按照逆变器功率器件开关状态，可得到以下6 个非零电压矢量U1（001）、U2（010）、U3（011）、U4（100）、U5（101）、U6（110）以及2 个零矢量U0（000）、U7（111），如图3 所示。

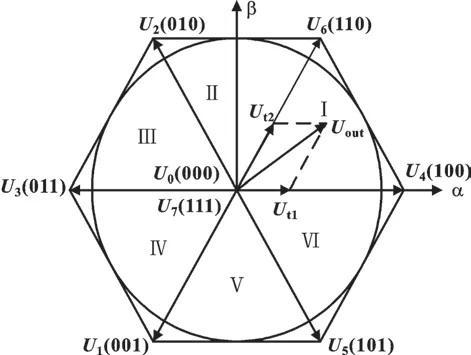
图3 电压空间矢量图Fig.3 Voltage space vector diagram

电压空间矢量图由8 个基本电压矢量共同组成并六等分。每个扇区内电压矢量都可由相邻两基本电压矢量和零矢量作用一定时间合成，并且圆形区域为正常调制区域。

3 模糊PI 控制器的设计

模糊控制是基于模糊理论，根据专家知识和先验实践经验制定模糊规则，对偏差量和偏差变化率进行实时调整，做出最优决策的智能控制方法［16］。它不依赖于精确模型，对于时变、非线性系统具有良好的控制效果和广泛的适应性，且控制算法具有较高控制精度。模糊化、模糊推理以及解模糊化是模糊控制器的主要构成。文中的模糊PI 控制器是将模糊控制与PID控制相结合，利用模糊控制算法智能调节PI 参数，从而实现高精度控制。控制结构框图如图4 所示。

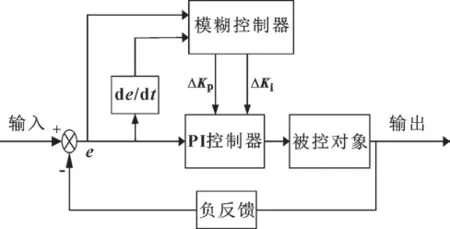
图4 模糊PI 控制器结构框图Fig.4 Structure block diagram of fuzzy PI controller

模糊PI 控制器将转速目标值与反馈值做差并得到转速误差e，模糊控制器的输入即为计算得到的误差e和误差偏差率ec，对输入变量依次进行模糊处理、根据规则完成推理并将模糊变量数值化后，将比例系数增量ΔKp、积分系数增量ΔKi作为控制器的输出，然后经PI 控制器完成参数累积，最终得到经过调整的PI 参数，从而实现对电机转速的调节。经过调整后的PI 参数为

其中：Kp0、Ki0分别是PI 控制器的比例、积分系数初始值；ΔKp、ΔKi分别为比例、积分系数的修正值，经模糊推理得出。

3.1 模糊化

模糊化的定义是将精确的输入变量数值转化为与之对应的模糊的语言变量值。令｛NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）｝ 作为语言变量模糊集合。图5 展示了变量的隶属度函数，梯形函数分布在两端，中间部分全为三角函数。输入变量的论域相同，为［-5，5］；输出变量ΔKp、ΔKi的论域分别为［-3，3］、［-1，1］。

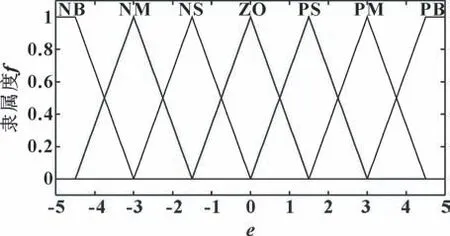
图5 输入输出变量隶属度函数Fig.5 Membership functions of input and output variables

3.2 模糊规则的制订与解模糊化

模糊控制器性能的好坏，关键在于模糊规则的制订。ΔKp、ΔKi的模糊推理规则如表1 所示。

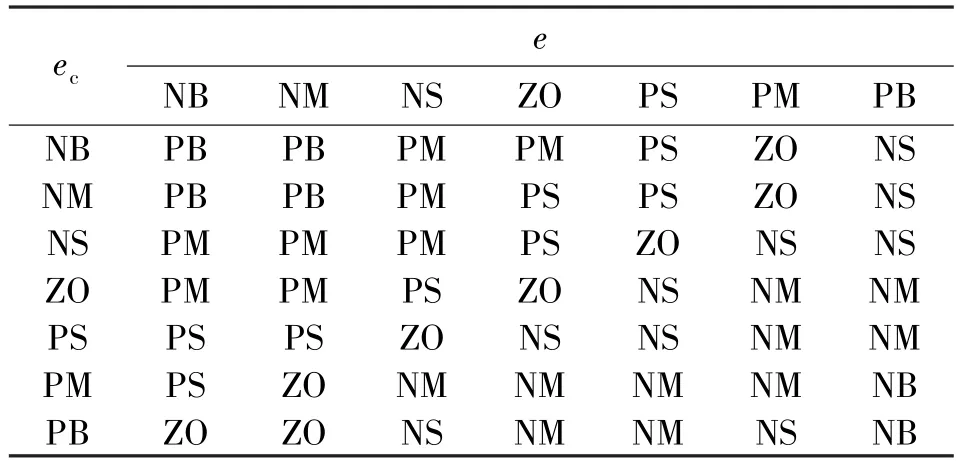
表1 ΔKp、ΔKi 的模糊规则Tab.1 Fuzzy rule of ΔKp，ΔKi

根据给出的模糊规则，在得到两输入变量的模糊集合后，采用Mamdani 推理方法，便能得到两个输出量的模糊集合。输出量ΔKp、ΔKi与输入量e和ec的关系如图6 所示。

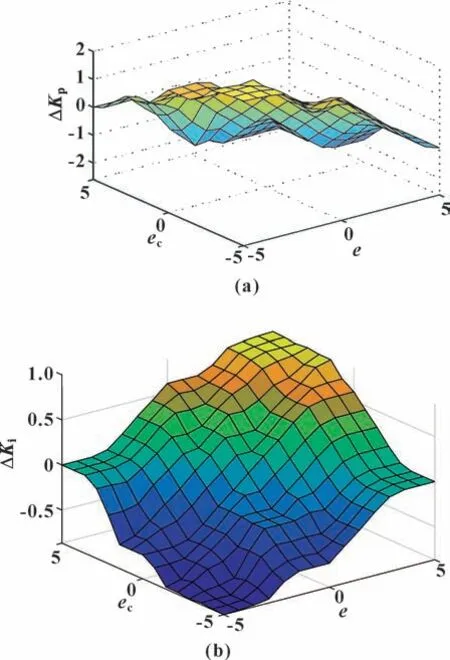
图6 输出量ΔKp（a）、ΔKi（b）的模糊规则面Fig.6 Fuzzy regular surfaces of outputs ΔKp（a），ΔKi（b）

经过模糊推理后的输出量为模糊量，要进一步转换为精确量以作用于控制参数，即解模糊化。在解模糊化过程中，本文作者采用加权平均法进行处理，具体公式为

式中：Ip、Ii分别为模糊推理输出的比例、积分模糊变量；μ（Ip）和μ（Ii）分别对应Ip、Ii的隶属度。

4 建模及仿真分析

4.1 永磁同步电机控制系统仿真分析

为验证所设计的模糊控制算法应用于PMSM 的有效性，采用仿真方法，观察在模糊控制的作用下，PI 控制参数自调整的有效性及其控制性能。被控电机参数如表2 所示。

表2 永磁同步电机参数Tab.2 Parameters of PMSM

在仿真过程中，两种控制算法的电流环PI 控制器参数不随时间变化，Kpd＝Kpq＝20，Kid＝Kiq＝2。传统PI 控制器转速环参数分别为Kp＝10，Ki＝1，并作为模糊PI 控制器的初始参数。设定当t＝0 s时，电机负载转矩为0 N·m，电机转速为1 000 r／min条件下使电机由静止开始启动，然后在t＝0.1 s 时突变负载为10 N·m，两种算法的结果对比如图7、8 所示。

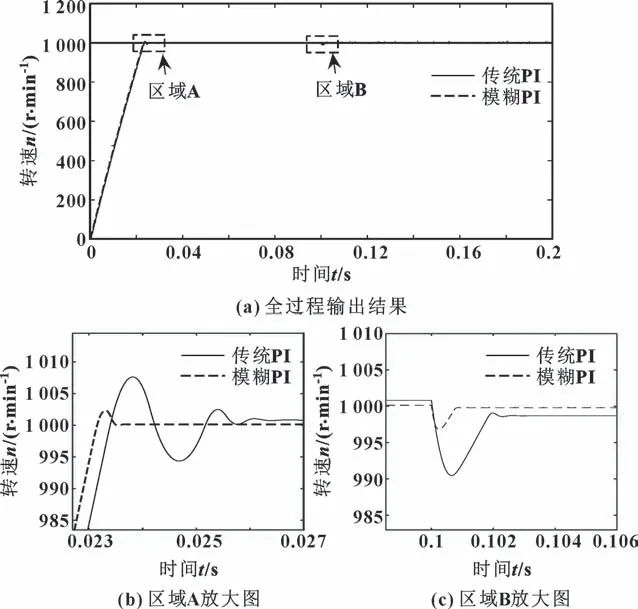
图7 模糊PI 与传统PI 转速输出结果对比Fig.7 Comparison of output speed between fuzzy PI and traditional PI：（a）output results of the whole process；（b）enlarged view of area A；（c）enlarged view of area B

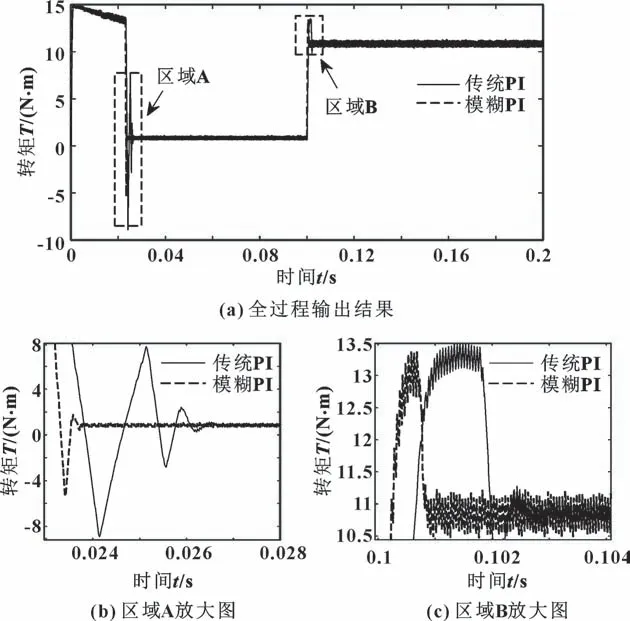
图8 模糊PI 与传统PI 转矩输出结果对比Fig.8 Comparison of output torque between fuzzy PI and traditional PI：（a）output results of the whole process；（b）enlarged view of area A；（c）enlarged view of area B

由图7、8 可知：在相同仿真环境下，输出转速在传统PI 控制器作用下表现出较大的超调量，最高可达0.75%，且出现明显的震荡；在0.1 s 时刻负载突增时，转速波动幅度较大，系统调节时间为2.5 ms，且存在明显的稳态误差。而在此基础上，模糊PI 控制器的输出转速超调量小于0.2%，且负载突增时转速波动幅度小，调节时间小于0.8 ms，转矩响应迅速无抖动现象。因此，本文作者所设计的模糊PI控制器，在相同的初始参数条件下，有效地实现了对PI 参数的自调整，并改善了原PI 控制器的动静态响应特性，能在目标转速阶跃及负载干扰中提升电机调速的动态响应速度、缩短调节时间并减少了稳态误差，提升了系统的鲁棒性和抗干扰性。

4.2 控制系统对电动油泵调速仿真分析

为验证文中所提出的模糊PI 控制算法调节电动油泵的性能，选用车辆在紧急制动时CVT 所处极限工况下对电动油泵实际转速需求作为控制目标。首先将CVT 液控系统的流量需求转换为电动油泵的目标转速，需构建流量与电机转速的关系：

式中：n是电机转速；ηE是泵的容积效率；V是油泵排量，为5 mL／r ；Q是电动油泵流量，在该工况下油泵所提供的流量主要由两部分构成，包括由CVT 调速所需的流量Qshift和泄漏流量Qleakage。对于Qshift和Qleakage，有

其中：λ为带轮锥角；As为从动油缸有效作用面积；di／dt为速比变化率；Rs为从动轮工作节圆半径，可由速比计算得到；k为泄漏系数；p为工作压力。根据上述公式可知，流量Q可由CVT 参数、速比和压力计算得出。在实际过程中，由于存在能量损失，因此电机驱动功率与油泵输出的液压功率存在一定的效率转换，具体如下：

式中：η为能量转换效率，则驱动转矩T为

对于CVT 油泵的流量供给来说，最苛刻的工况是紧急制动（Emergency Stop）。当CVT 运行在最小速比时，发动机转速较低，而此时如果车辆出现紧急制动工况，那么在停车之前，液控系统要快速将金属带从最小速比控制到最大速比位置。选取实车测试中的某一紧急制动工况（初速度100 km／h，末速度为0）下，以最大强度制动，此时CVT 的速比回调速度如图9 所示（2 s 左右从最小速比0.437 回位到最大速比2.623）。通过计算可得到该过程中所需的流量。利用式（11）（13）便可得电机的转速与负载，将其作为系统的输入信号。

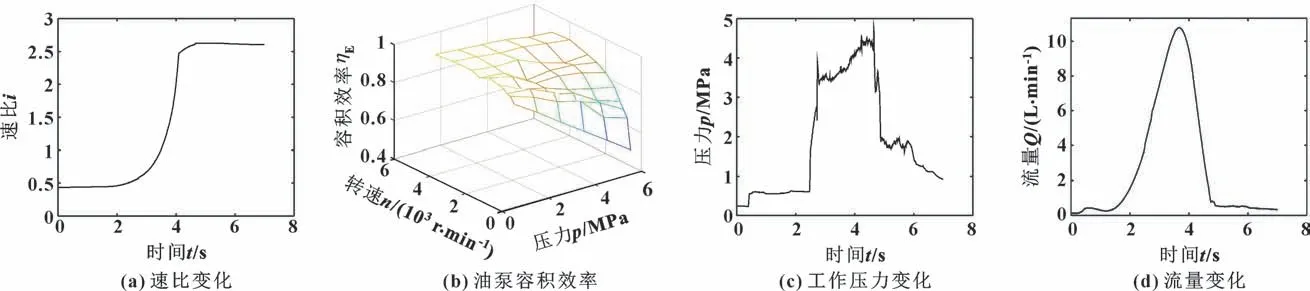
图9 紧急制动工况下测得的实验数据Fig.9 Experimental datas measured under emergency stop condition：（a）speed ratio change；（b）volumetric efficiency of oil pump；（c）working pressure change；（d）flow change

综合以上理论分析后，根据模块化的建模思想，在MATLAB／Simulink 软件中搭建如图10 所示的电动油泵调速系统的仿真模型。将通过变换得到的转速和负载转矩作为系统的输入，输出结果如图11、12 所示。

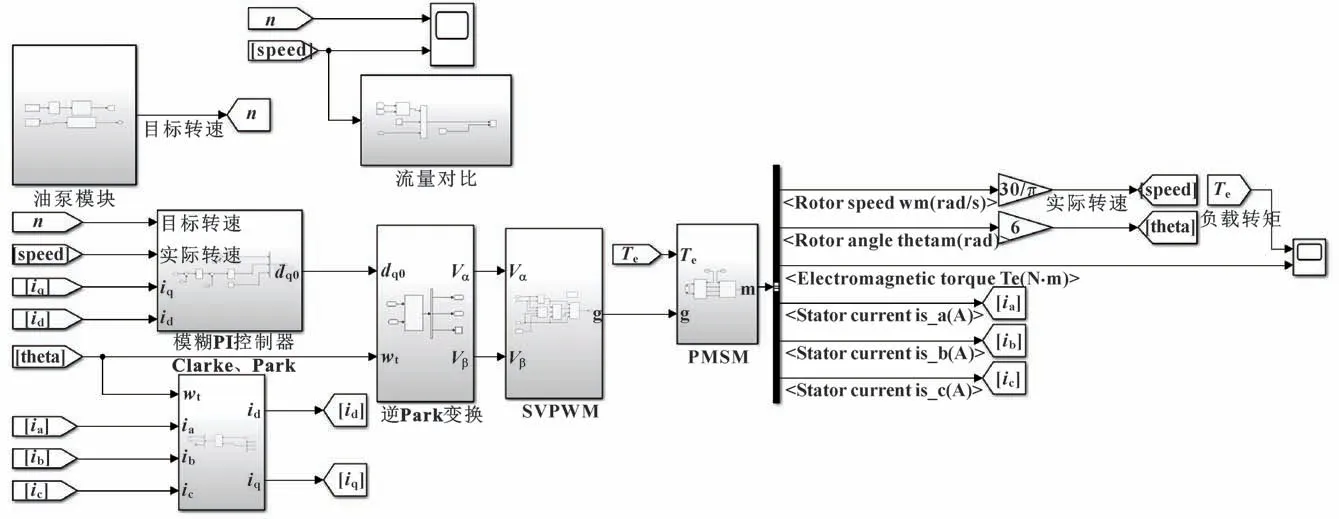
图10 电动油泵调速系统仿真模型Fig.10 Simulation model of EOP speed control system

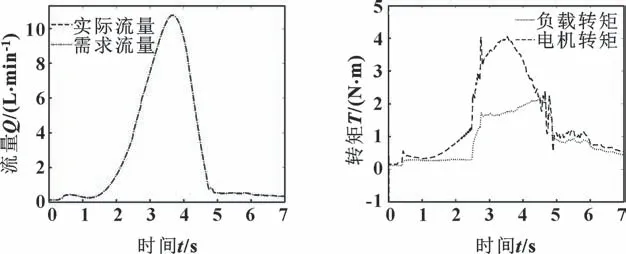
图11 流量输出结果 图12 转矩输出结果Fig.11 Result of flow output Fig.12 Result of torque output

从图11、12 中能够看出：设计的控制系统能确保电动油泵输出流量良好地满足需求流量，电动油泵转矩能根据外部负载转矩做出快速响应并满足转矩要求，既保证了CVT 的正常工作，又极大程度上减少了溢流损失。说明设计的基于模糊PI 的控制算法适用于永磁同步电动油泵，且具有良好的控制性能，能满足CVT 的供油需求。

5 结论

为实现一种兼具良好动静态控制能力、具有工程化实用价值的油泵电机控制器，本文作者将模糊PI算法用于PMSM 油泵电机的控制。设计了模糊控制器，并利用仿真手段验证了其对PI 参数自调整的有效性，进一步地将其应用于CVT 液控系统。结果表明：采用模糊PI 算法的控制系统，无论是在转速阶跃还是负载突变的情况下，其性能都优于传统PI 控制系统，获得了更好的动态响应和抗干扰性。同时，该算法能精准控制电动油泵的输出流量，不仅能满足CVT 正常工作的需求，而且有效减少了溢流损失。