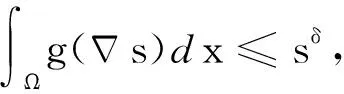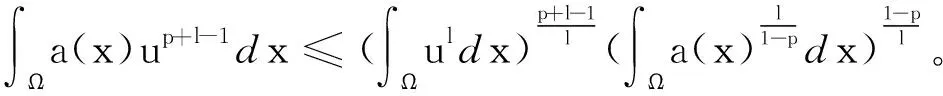具有吸收项的加权反应扩散方程解的性质
杨来君,杨 梓
(兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
近年来,许多文献研究了抛物方程和抛物系统解的全局存在性,解的爆破时间的上下界、爆破集、爆破速率和解的渐近行为等解的其他性态[1-5],其中,反应扩散方程的解全局存在性和爆破以及何时发生爆破是重要的研究方向。目前研究爆破时间上界的方法较多[6]而研究爆破时间下界的方法较少,Payne等在研究爆破时间下界方面做了开创性工作[7-10]。有关抛物方程和抛物系统的上下界在物理学、天文学、生物学、化学等领域有着广泛的应用[11-12]。文献[13]研究具有加权非局部源和Robin边界条件下半线性抛物方程
(1)
的解的爆破情况,利用微分不等式技巧,得到了在高维空间中解的爆破时间的下界。文献[14]研究了具有加权梯度非线性反应扩散方程
(2)
爆破时间的界。利用上下解方法和微分不等式技巧,得到了在适当的测度意义下解在有限时间爆破的充分条件,同时得到在高维空间中爆破时间的上下界并给出一些应用实例。文献[15]研究具有加权非局部梯度吸收项的反应扩散方程
(3)
通过构造辅助函数,运用微分不等式技巧,得到了解的全局存在性和爆破时间的上下界。
受以上文献的启发,考虑到边界也会受到非局部的影响,本文研究具有加权非局部梯度吸收项的反应扩散方程
(4)
1 解的全局存在性
定理1设Ω⊂RN(N≥1)是一个具有光滑边界∂Ω的有界域,权函数a(x)满足(A1)或(A2)且函数f和g满足条件
(5)
(6)
则当t>0时问题(4)的非负古典解u(x,t)存在,其中
a1≥0,a2≥0,q>0,l>1,m>max{σ+2,2σ-1,p,l},
(7)
ε在证明中给出。
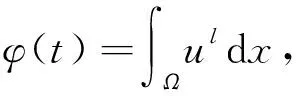
(8)
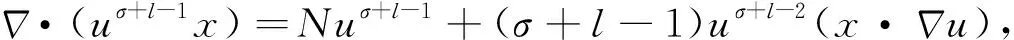
(9)
其中
将式(9)代入式(8),可得
(10)
通过Hölder不等式和Young不等式,可得
(11)
(12)
在式(7)的条件下,由Hölder不等式,可得
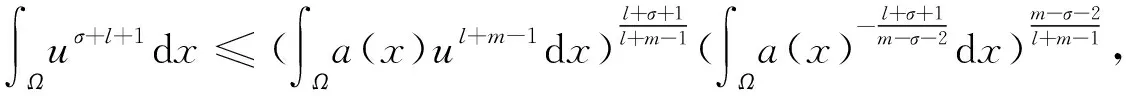
(13)
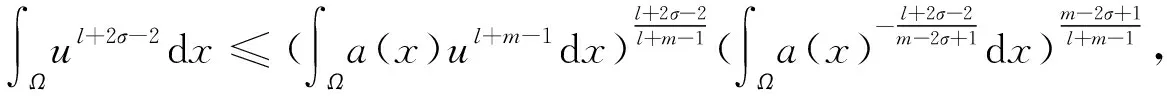
(14)
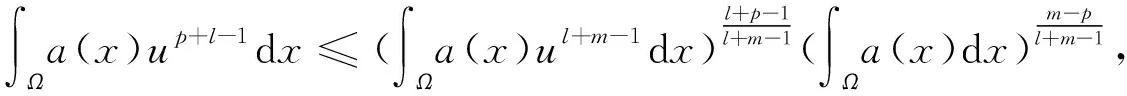
(15)
(16)
将式(13)~(16)代入式(12)并使用Poincare不等式,可得
(17)
其中,
(18)
由式(18)得:当φ(t)>(P1+P2+P3)q-GP4G-q≥1时,φ′(t)≤0;当0<φ(t)<1时,取Q=min{σ+2,2σ-1,p},可得
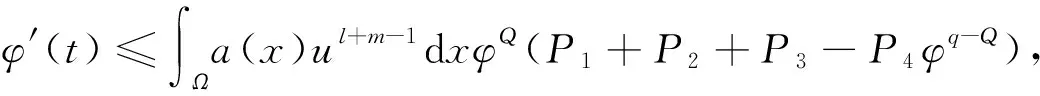
(19)
由式(19)得,当0<(P1+P2+P3)q-QP4Q-q<φ(t)<1时,φ′(t)≤0。
取适当的a1,a2,ε,使其满足式(18)(19)两个条件。由此可得,函数φ(t)是单调递减的;因为φ(t)>0,所以对于所有的t>0,解u(x,t)存在。接下来,给出爆破的定义,并分别得到爆破时间的上界和下界。
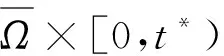
则称u(x,t)在有限时间内爆破。
2 爆破时间的上界
定理2设Ω⊂RN(N≥1)是一个具有光滑边界∂Ω的有界域,u(x,t)是问题(4)的非负古典解;权函数a(x)满足(A1)或(A2),θ(0)≥0且函数f和g满足如下条件:
(20)
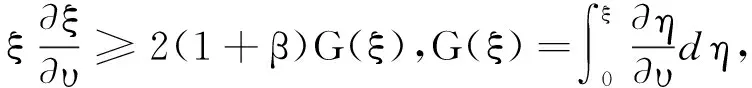
(21)
则解u(x,t)在有限时间t* (22) 如果β=0,则有T=∞。 证明由式(4)、格林公式、式(20)~(22),可得 (23) 由式(4)(22)和格林公式,可得 由于θ(0)≥0,所以对∀t∈(0,t*),有θ(t)≥0。由式(23)及Schwarz不等式,可得 (24) 对式(24)从0到t进行积分,可得θ(t)(Ψ(t))-(1+β)≥θ(0)(Ψ(0))-(1+β),记M=θ(0)(Ψ(0))-(1+β),可得 θ(t)≥M(Ψ(t))1+β。 (25) 将式(25)代入式(23)并从0到t进行积分,可得 (26) 定理3设Ω⊂RN(N≥3)是一个具有光滑边界∂Ω的有界域,u(x,t)是问题(4)的非负古典解,权函数a(x)满足(A1)或(A2)且函数f满足式(5),g满足条件 (27) 则u(x,t)在有限时间t*发生爆破,且有 其中 (28) (29) 由式(9)可得 (30) 通过Hölder不等式和Young不等式,可得 (31) (32) (33) 其中C2=C2(N,Ω)是和空间维数N和区域Ω有关的常数。 在式(28)的条件下,由Hölder不等式和Young不等式,可得 (34) 在(28)的条件下,由Hölder不等式和式(33),可得 (35) 通过基本不等式 (36) 将式(36)代入式(35),可得 (37) 在式(28)的条件下,由Young不等式,可得 (38) 将式(38)代入式(37),可得 (39) 将式(34)(39)代入式(32)并取 得 (40) 其中 在式(28)的条件下,通过Hölder不等式,可得 (41) 将式(41)代入式(40),可得 (42) 其中 由式(42)可得 (43) 对式(43)两边从0到t积分,可得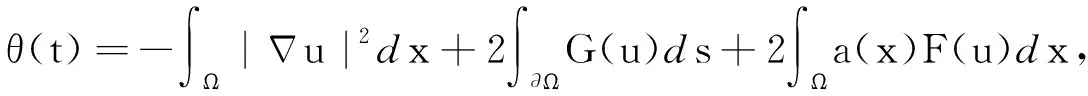
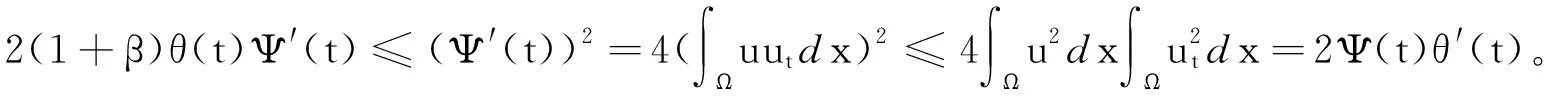

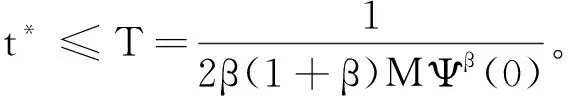
3 爆破时间的下界