一类具有非线性发生率的时滞戒烟模型
张子振,张伟诗,宋志强
(1.安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030;2.呼伦贝尔学院 机电工程学院,内蒙古 呼伦贝尔 021008)
2016年发布的《“健康中国2030”规划纲要》提出,鼓励政府机关、事业单位、医生和教师等群体发挥控烟引领作用,研究利用税收、价格调节等综合手段,提高控烟成效,到2030年,中国15岁以上的人群吸烟率应低于20%[1-2]。随着禁烟政策的实施以及国民素质的提高,吸烟行为在公共场合开始减少,吸烟行为对潜在吸烟人群的吸引也随着烟草危害的普及而逐渐减少,在社会上逐渐形成一种“吸烟流行饱和”的现象。
吸烟作为一种社会性行为,具有一定的社交功能,所以在传播形式上与慢性传染病相似,在人群中具有一定的传播性,一个人吸烟可能会使周围的很多人吸烟。很多生物数学领域的专家通过观察吸烟行为的流行规律,构建微分方程模型来研究吸烟行为的动力学性质。目前戒烟模型按照发生率主要分为双线性发生率和非线性发生率两种模型。在双线性发生率模型[3-6]中,学者假设吸烟人数与吸烟者的接触者数量成正比。然而,在实际生活中,接触者因为了解吸烟的危害而会对吸烟行为产生一定程度的抑制效应。因此,近年来具有非线性发生率的戒烟模型引起了学者关注[7-10]。本文在文献[7,9]的基础上,考虑戒烟者重新变为潜在吸烟者的恢复期时滞,提出了具有非线性发生率的时滞戒烟模型
(1)
该模型将总人群分为潜在吸烟者、轻度吸烟者、习惯吸烟者、戒烟者4个种群,分别用P(t),L(t),S(t),Q(t)表示各个种群在t时刻的数量。Λ,β,c,κ,ε,∂,η,v,τ为模型(1)的参数。其中,Λ指潜在吸烟群体的常数输入率,βS指习惯吸烟者对于潜在吸烟者的同化能力,P+S+c反映了在社区中习惯吸烟者和潜在吸烟者人数在增加时产生的饱和效应带来的对吸烟行为产生的抑制作用,κ指戒烟者向潜在吸烟者转化的率,ε指所有人群的自然死亡率,∂指轻度吸烟者向习惯吸烟者的转化率,η是习惯吸烟者的戒烟率,v是习惯吸烟者因吸烟而额外增加的死亡概率,τ是戒烟者成为潜在吸烟者的恢复期时滞。本文主要研究时滞动力系统中τ对系统稳定性的影响。
1 基本再生数和吸烟平衡点
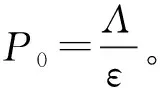
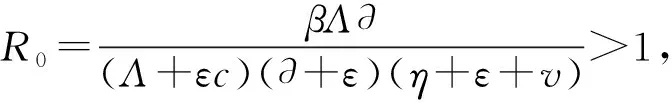
2 Hopf分岔的存在性
模型(1)在吸烟平衡点E*=(P*,L*,S*,Q*)处的雅可比矩阵为
其中,
求其特征方程可得
λ4+γ3λ3+γ2λ2+γ1λ+γ0+(Ψ3λ3+Ψ2λ2+Ψ1λ+Ψ0)e-λτ=0,
(2)
其中,
γ0=h11h22h33h44+h13h21h32h44-h11h23h32h44,
γ1=-h11h22(h33+h44)-(h11+h22)h33h44-h13h21h32+h23h32(h11+h44),
γ2=h11h22+(h11+h22)h33+(h11+h22+h33)h44-h23h32,γ3=-(h11+h22+h33+h44),
Ψ0=λ44(h11h22h33+h13h21h32-h11h23h32)-λ14h21h32h43,
Ψ1=-λ44(h11h22+h11h33+h22h33-h23h32),Ψ2=λ44(h11+h22+h33),Ψ3=-λ44。
在τ=0的情况下,特征方程(2)变为
λ4+(γ3+Ψ3)λ3+(γ2+Ψ2)λ2+(γ1+Ψ1)λ+γ0+Ψ0=0。
(3)
根据Hurwitz判据可知,如果式γ0+Ψ0>0,(γ2+Ψ2)(γ3+Ψ3)>(γ1+Ψ1),(γ1+Ψ1)(γ2+Ψ2)(γ3+Ψ3)>(γ0+Ψ0)(γ3+Ψ3)2+(γ1+Ψ1)2成立,在τ=0的情况下,模型(1)将会局部渐近稳定。
在τ>0的情况下,假设方程(2)的解为λ=iϖ(ϖ>0),分离实部和虚部,可以得到
(4)
对方程组(4)进行处理可得
ϖ8+Ω3ϖ6+Ω2ϖ4+Ω1ϖ2+Ω0=0,
(5)
其中
令ϖ2=ζ,方程(5)变为
ζ4+Ω3ζ3+Ω2ζ2+Ω1ζ+Ω0=0。,
(6)
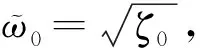
对特征方程(2)中的λ求关于τ的导数,可得

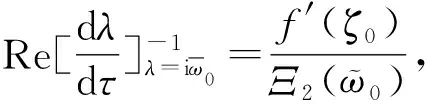
利用文献[11]中关于Hopf分岔存在性的相关理论,得到下列结果。
定理1当模型(1)的基本再生数R0>1时,若τ∈[0,τ0)则模型(1)局部渐近稳定,若τ>τ0则模型(1)产生Hopf分岔,并在正平衡点E*=(P*,L*,S*,Q*)处产生分岔周期解。
3 分岔周期解的方向和稳定性
令τ=τ0+χ,t→(t/τ),其中χ∈R。同时令u1(t)=P(t)-P*,u2(t)=L(t)-L*,u3(t)=S(t)-S*,u4(t)=Q(t)-Q*。则模型(1)变为
(7)
其中,
ut=(u1(t),u2(t),u3(t),u4(t))T∈C([-1,0],R4),Tχ(φ)=(τ0+χ)(J1φ(0)+J2φ(-1)),
其中,
129 CT signs and diagnostic significance in patients with benign or malignant pulmonary ground-glass nodules
根据Riesz表示定理可知,存在有界变差函数ρ(θ,χ),其中当θ∈[-1,0]时有

对φ∈C,可以选取ρ(θ,χ)=(τ0+χ)(J1δ(θ)+J2δ(θ+1)),其中δ(θ)为狄克拉函数。之后,对φ∈C([-1,0],R4),定义
且
以及双线性内积

(8)
其中ρ(θ)=ρ(θ,0)。

其中,
其中,
最后,计算得到下列系数:
(9)
通过文献[11]中对分岔周期解相关性质的描述,可以推出下列定理。
定理2当μ2>0时,模型(1)在τ0处产生的Hopf分岔将是超临界的,反之则为次临界;当β2>0时,分岔周期解是不稳定的,反之则为稳定;当T2>0时,分岔周期解为递增,反之则为递减。
4 仿真示例
选取Λ=1,β=0.76,c=10,κ=0.26,ε=0.01,∂=0.14,η=0.041,v=0.0019,则可以得到模型(1)的示例模型
(10)
因此,可得R0=12.19>0,用Matlab软件计算得示例模型(10)存在唯一吸烟平衡点E*(5.2385,20.8211,55.1032,8.3675),进而计算得τ0=5.8976。在τ0两边分别随机选取一个数值进行验证。当选取τ=5.3379∈(0,τ0)时,示例模型(10)的状态轨迹与相图分别如图1、2所示,可以看到此时的模型中各种群数量局部渐近稳定。当选取τ=5.9014>τ0时,示例模型(10)将失去稳定性,并在吸烟平衡点E*(5.2385,20.8211,55.1032,8.3675)处产生Hopf分岔, 状态轨迹和相图如图3、4所示。

图1 当τ=5.3379时,示例模型(10)的状态轨迹

图2 当τ=5.3379时,示例模型(10)的相图

图3 当τ=5.9014时,示例模型(10)的状态轨迹

图4 当τ=5.9014时,示例模型(10)的相图
此外,经过计算得到公式(9)的各项系数的数值,其中C1(0)=-2.1031+i0.8912,λ′(τ0)=0.5581-i0.7572,μ2=3.7683>0,β2=-4.2062<0,T2=4.0953。由此可知示例模型(10)在τ0=5.8976处产生的Hopf分岔是超临界的,并且是稳定递增的。
5 小结
本文扩展了文献[7,9]的研究,提出了一类具有非线性发生率的戒烟模型,并引入了戒烟者重新变为潜在吸烟者的潜伏期时滞,研究了一类具有非线性发生率的时滞戒烟模型。在对模型的基本性质进行了推导后,选择时滞作为分岔参数,利用特征值法计算得到模型局部渐近稳定和Hopf分岔存在的充分条件,之后利用中心流行定理推导判断产生的Hopf分岔方向和周期大小等性质。通过仿真模拟可以看到,时滞的不同取值会对模型的稳定性进行影响,当时滞取值低于临界值时,此时模型中各种群中个体数量会在平衡点附近保持稳定,此时吸烟行为的流行易于控制。而当时滞的取值超过临界值时,模型中的潜在吸烟者、轻度吸烟者、习惯吸烟者和戒烟者群体的个体数量会变得周期震荡并产生Hopf分岔,吸烟行为的流行难以控制。

