一类曲率方程解的梯度估计

吴婷婷,韩 菲,孙文静

(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)

0 引言

平均曲率方程是偏微分方程中的一类,对其的研究主要集中在解的存在性、唯一性、正则性。若要得到解的存在性,需建立解的边界梯度估计。

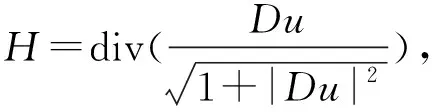
很多学者已对这两种形式的平均曲率方程进行了广泛的研究[1-4]。

文献[5]利用微分的方法研究了具有Neumann边值问题的平均曲率方程

解的梯度估计,给出了此类平均曲率方程Neumann问题解的存在性。文献[6]通过曲面上的活动标架法研究了具有Neumann边值问题曲率方程解的梯度估计

此方法简化了文献[5]研究平均曲率方程解的梯度估计的证明。文献[7]研究了抛物型方程

其中:fz(x,z)≥-k,k>0,Ω∈Rn为有界的C3区域,n≥2,T为固定的正常数。该文弱化了fz(x,z)的条件,并且得到了解的梯度估计。文献[8]研究了方程

其中f(x,u)是定义在Ω×R上的光滑函数,得到了此类方程解的梯度估计以及解的收敛性。

受上述研究启发,将利用文献[4-6]的方法对文献[8]研究的具有Neumann问题的平均曲率方程进一步推广,即研究抛物方程

其中f(x,u,Du)是定义在[0,1]×R×Rn上的光滑函数。

1 主要结果

定理1 假设Ω=[0,1],f是定义在Ω×R×Rn上的光滑函数,假设u(x,t)是方程

(1)

的解,其中

fz(x,z,p)≥-k,k≥0。

(2)

假设存在一个正常数L1满足

(3)

那么对于t∈[0,T],就会有|ux(x,t)|≤C,其中

推论1 假设Ω=[0,1],f是定义在Ω×R×Rn上的光滑函数,则抛物方程

有光滑解u=u(x,t)。

上述方程两边同时对t求导,可得

(4)

而

(5)

将式(4)代入式(5)可得

假设e-ktut在(x0,t0)处取得非负极大值,通过极值原理,则可分为3种情况:(a)t0=0;(b)t0>0且e-ktut在[0,1]×[0,t0]内恒为常值函数(则一定是ut(x,0));(c)t0>0且x∈{0,1}。

接下来得到u的C1估计。

定理1的证明构造辅助函数

Φ(x,t)=log(ux)2+g(x)+λ,

其中,g(x)=x2-x,λ将在后面给出定义。假设在点(x0,t0)处Φ(x,t)达到非负极大值,其中x∈[0,1]。分3种情形进行讨论。

情形1x0=0或x0=1,根据边界条件ux(0,t)=a,ux(1,t)=b可得

情形3 (x0,t0)∈(0,1)×(0,T],由函数在极值点的性质,可得

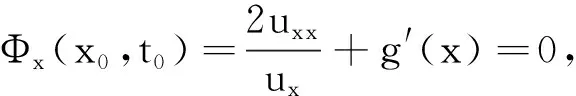
(6)

(7)

由ut=uxxv-2-f(x,u,Du),可得

(8)

由式(6)知

(9)

将式(8)(9)代入式(7)可得

其中

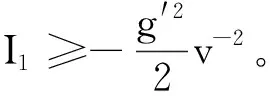
(10)

则

因此

即v(x0,t0)≤C。

由于Φ(x,t)在点(x0,t0)处取得非负极大值,所以对任意的(x,t)有

Φ(x,t)≤Φ(x0,t0)=log(ux)2(x0,t0)+g(x0)-λt0≤log(C)2+g(x0)-λt0。

即

log(ux)2+g(x)-λt≤log(C)2+g(x0)-λt0。

故

log(ux)2≤log(C)2+g(x)-λ(t-t0)≤C。

通过上述3种情形,得到了u的C1估计,从而完成了定理1的证明。

2 结论

通过微分的方法引入适当的辅助函数,利用函数在极大值点的性质研究一类具有Neumann边值条件的曲率方程解的梯度估计。证明过程主要是分为3种情况,即在边界达到极大值、初始时刻达到极大值以及内部取到极大值,研究解的C0估计、C1估计以及ut估计,进而给出此类方程解的存在性。解的先验估计与所给方程中的函数f有关,讨论的方程是f依赖于x,u,Du时解的梯度估计,对此类具有Neumann问题的平均曲率方程可以进一步推广到复空间上研究讨论。