图的Aα-谱半径的界*
靳 龙,陈鸿章
(闽南师范大学 数学与统计学院,福建 漳州 363000)
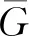
图G的邻接矩阵和度对角矩阵分别记为A(G)和D(G).A(G)的最大特征值(记作ρ(G))称为G的谱半径.G的无符号拉普拉斯矩阵定义为Q(G)=D(G)+A(G),其最大特征值(记作q(G))称为G的无符号拉普拉斯谱半径.Nikiforov[2]定义G的Aα-矩阵(α∈[0,1])为
Aα(G)=αD(G)+(1-α)A(G).
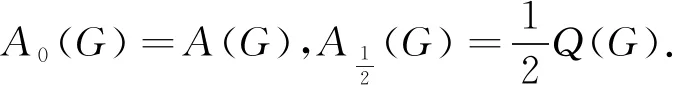
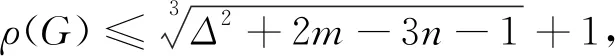
本文将[11]中的结果推广到G的Aα-谱半径ρα(G)上,得到了当G不含C3和C4作为子图时ρα(G)的可达上界,同时也给出了ρα(G)的新的下界.
1 相关引理
引理1.1[12]设P(x)是实系数多项式,P(Aα(G))的对应于顶点v的行和为Sv(P(Aα(G))),则
min{Sv(P(Aα(G)))}≤P(ρα(G))≤max{Sv(P(Aα(G)))},
其中等式成立当且仅当P(Aα(G))的各行和都相等.
引理1.2
其中等式成立当且仅当G为正则图.
引理1.3[14]设a1,…,an是正整数,则
2 G的Aα-谱半径的上界
Filipovski等[11]给出了不含C3和C4作为子图的图的谱半径的上界,我们将其结果推广到图的Aα-谱半径上.
引理2.1若G不含C3和C4作为子图,则对任意α∈[0,1]有
(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.
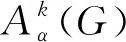
α2D2(G)+α(1-α)D(G)A(G)+(1-α)αA(G)D(G)+(1-α)2A2(G),
故
由于
(αD(G)+(1-α)A(G))(αD(G)+(1-α)A(G))(αD(G)+(1-α)A(G))=
α3D3(G)+α2(1-α)D2(G)A(G)+α2(1-α)D(G)A(G)D(G)+
α(1-α)2D(G)A(G)A(G)+(1-α)α2A(G)D(G)D(G)+(1-α)2αA(G)D(G)A(G)+
(1-α)2αA2(G)D(G)+(1-α)3A3(G).

因此
(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ,
即
(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.
根据引理2.1,有
(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.
注2.2若G是k-正则图,即ρα=δ=Δ=k且m=nk/2,则
注意到A0(G)=A(G),有以下推论.
推论2.3[11]若G不含C3和C4作为子图,则
推论2.4 若G不含C3和C4作为子图,则
q3(G)-δq2(G)+δq(G)≤6Δ3+2Δ2(1-δ)+4m-2nδ.
定理2.5 若G不含C3和C4作为子图,则对任意α∈[0,1]有
其中
E=(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.
证明给定α∈[0,1],设多项式
p(x)=x3-δ(1-α)x2+(1-α)2δx-E.
注意到
27E2>(1-α)6δ4+18(1-α)3δ2E,
可知p(x)的判别式为
D(p)=-4(1-α)6δ3+(1-α)6δ4+18(1-α)3δ2E-4(1-α)3δ3E-27E2<0.

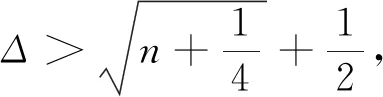
证明用Newton-Raphson方法[16]逼近如下多项式的实根:
p(x)=x3-δ(1-α)x2+(1-α)2δx-((2-α)αΔ3+(1-α)2Δ2+
2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ).
由于
p(δ)=αδ3+(1-α)2δ2-((2-α)αΔ3+(1-α)2Δ2+
2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ)<0,
p(Δ)=(1-2α+α2)Δ3-(1-α)2(δ+1)Δ2+(1-α)2δΔ-2(1-α)2m+(1-α)2nδ>0,
故p(x)有唯一的实根xα∈(δ,Δ).取初始值x0=Δ进行迭代,计算第一次迭代可得
由于函数p(x)在区间[xα,Δ]上是下凸的,故p(x)在点(Δ,p(Δ))处的切线与x轴的交点在xα的右侧.所以ρα(G)≤xα≤x1.
3 G的Aα-谱半径的下界
Nikiforov[2]给出了G的Aα-谱半径的下界:
(1)
其中等式成立当且仅当G为正则图.本节利用G的顶点度的方差
对上述结果进行改进.设G的度序列为Δ=dv1≥dv2≥…≥dvn=δ.
定理3.1对任意α∈[0,1]都有
(2)
其中等式成立当且仅当G是正则图.
证明由引理1.2和引理1.3可得
(3)
注意到
并且
代入(3)便得到

注3.2文献[17]给出了G的Aα-谱半径的如下下界:
(4)

定理3.3
(5)
其中等式成立当且仅当G为正则图.
证明我们有
(6)
由引理1.2可得
(7)
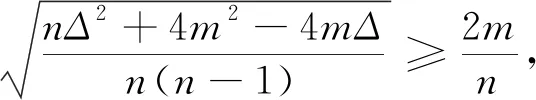
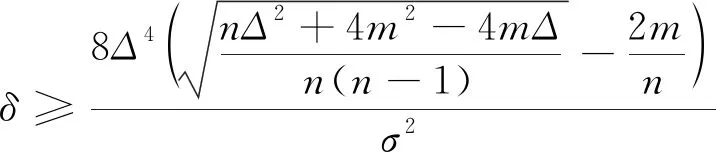
结合定理3.1和3.3,可得
定理3.6


定理3.7

致谢本文得到数字福建气象大数据研究所和数据科学与统计重点实验室的资助.

