关于丢番图方程2py2=x(x+1)(x+2)

何宗友

(深圳市京田精密科技有限公司,广东 深圳 518118)

1875年Lucas[1]问丢番图方程

6y2=x(x+1)(2x+1)

(1)

的正整数解是否仅有(x,y)=(1,1),(24,70).1919年Watson[2]利用椭圆函数对该问题作出了肯定的回答,1952年Ljunggren[3]利用四次代数扩域中的Pell方程给出了一个新的证明,然而他们的证明都不是初等的.1969年Mordell[4]问能否给出一个初等证明.该问题在1981年被Richard[5]收入UnsolvedProblemsinNumberTheory一书中.1985年马德刚[6]给出一个初等证明,但其篇幅长达一万余字;同年徐肇玉和曹珍富[7]也宣布给出了一个初等证明.1990年洪伯阳[8]问能否给出简短的初等证明.1994年笔者[9]简化了文献[6]的部分初等证明;2023年笔者[10]给出了一个十分简短且直接的初等证明.注意到丢番图方程

6y2=x(x+1)(x+2)

(2)

在2|x时就是方程(1),因而此时方程(2)仅有两组正整数解(x,y)=(2,2),(48,140).1996年曹珍富[11]证明了当p是奇素数时,丢番图方程

2py2=x(x+1)(x+2)

(3)

管训贵[12]提出了如下猜想:设素数p≡1(mod 8),则方程(3)的正整数解只有

(p,x,y)=(17,16,12),(577,576,408),(665857,665856,470862).

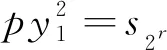
1 相关引理

引理1[13]设p是奇素数,则丢番图方程4x4-py2=1的正整数解只有

(p,x,y)=(3,1,1),(7,2,3).

引理2[14,15]设p是奇素数,则丢番图方程x4-2py2=1的正整数解只有(p,x,y)=(3,7,20).

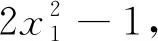
引理5[18,19]设L,M是整数,L>0,gcd(L,M)=1,定义Lehmer数Pn为

这里t是整数.

2 主要结果的证明

我们主要证明定理1.

设方程(3)在p≡1(mod 8)时有正整数解(x,y).注意到x+1与x(x+2)互素,故有以下四种情况.

情况12p|x+1.此时可设

(4)

情况22|x+1,p|x(x+2).此时可设

(5)

情况32p|x(x+2).此时可设

(6)

情况4p|x+1,2|x(x+2).此时可设

(7)

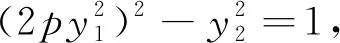
最后考虑情况4.由(7)得

(8)

(9)

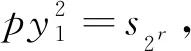
(10)

(i)h=1.此时由(10)得

(11)

或

(12)

(ii)h=q.此时由(10)得

(13)

或

(14)

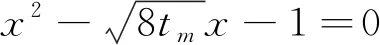
(15)

(16)

由(16)得

(17)

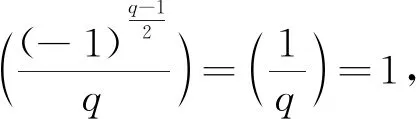
(18)

定理1证毕.

只需在定理1的证明过程中将(8)中的系数2改为d,重复(8)之后的步骤,就可证明定理2.

致谢泰州学院的管训贵教授对本文提出了宝贵的修改意见,笔者在此表示衷心的感谢!