基于数字孪生的滚动轴承状态监测研究*

吴静远,舒启林,魏永合

(沈阳理工大学机械工程学院,沈阳 110159)

0 引言

轴承为旋转机械中最关键的零件,它的健康状态将直接影响整个设备的运行效率,因此对它运行状态的监测具有重要的现实意义[1-2]。

数字孪生技术在近年受到广泛关注,但由于相关支持技术的发展相对不足等因素的影响,数字孪生在刚被提出的时候没有获得快速的关注和发展[3]。近年来,数字孪生在智慧城市、机械装备、军事等领域得到了良好的应用与研究[4-5]。赵永胜等[6]利用数字孪生技术对飞机装配对接过程实现监控、优化对接参数,将装配中的位置偏差和姿态偏差大幅降低。YU[7]基于非参贝叶斯网络利用数字孪生技术提出了一种对设备进行健康监测的方法,提高了模型的学习能力。SODERBERG等[8]提出一种概念,利用数字孪生技术在产品的设计、生产阶段进行监控和优化。

在故障预测与健康管理(prognostics health management,PHM)领域,相较于传统的方法,利用数字孪生技术可以获得在实际生产中难以获得的参数,以及一些无法测得的状态量。另外,将数字孪生技术应用在对轴承的状态监测中,整个过程不会由于传感器的安装影响设备的运行,也不需要终止设备运行进行观测,因此可以更低成本地地跟踪轴承的各个参数,从而实现对轴承的状态检测。然而,由于机械结构的复杂性,以及运行时受载荷和转速等冲击影响的复杂性,在实际应用中仍存在以下两个问题,一是如何准确地建立数字孪生模型,二是如何实现较低的计算成本。

Modelica是一种多领域建模方法,并配有建模语言[9]。其与使用Simulink等建模方法相比较,实现了以物理视角代替数学视角进行建模,能够更加准确地建立数字孪生模型。其与Anasys等使用有限元分析的方法相比较,实现了更低的计算成本,为以后研究模型的实时信息交互打下基础。

因此为了得到准确度高、计算更快速以及更符合物理拓扑关系的模型,本文创新地利用Modelica这一多领域建模方法,搭建滚动轴承的数字孪生模型。然后以实测信号和理论信号为依据,对模型的准确度进行验证,为滚动轴承的状态监测提供理论支持。

1 深沟球轴承动力学分析

首先对6205深沟球轴承进行动力学简化,本文采用滚动轴承5自由度简化的模型[10],如图1所示。该滚动轴承动力学简化模型,符合以下假设条件:所有组件都采用质量集中法;无惯性力矩;滚动体与内外圈接触面不存在任何几何误差;滚动体与内外圈之间的接触符合赫兹理论;所有阻尼均为线性粘性。

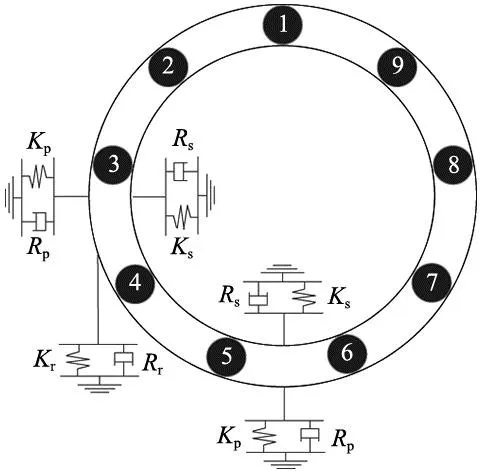
图1 5自由度滚动轴承模型

图1中,4个弹簧-阻尼系统分别连接在固定端以及内外圈上,另一个弹簧-阻尼-质量系统表示轴承的高频响应。内外圈各有一个X方向和1个Y方向的自由度,高频响应还有一个Y方向的自由度,因此这个简化模型共有5个自由度。

该模型的动力学动态微分方程为:

(1)

式中:ms、mp、mr分别代表内圈、外圈和谐振变换器的质量,Rs、Rp、Rr分别代表内圈、外圈和谐振变换器的阻尼值,Ks、Kp、Kr分别代表内圈、外圈和谐振变换器的刚度值,x,y代表各自由度上的位移量,f为赫兹接触力,F为外载荷。

若轴承的内外圈出现缺陷故障,则滚动体经过缺陷位置时会造成冲击进而影响振动信号的规律,出现故障特征频率。滚动轴承的故障特征频率由该轴承的参数决定,因此可以由此判断轴承的健康状态。对于外圈固定在基座上,同时接触角为0的深沟球轴承来说,其特征频率为:

(2)

式中:BPFI和BPFO分别为内圈故障特征频率和外圈故障特征频率,Nb、fs分别为滚动体数量和内圈转速,d和D分别为滚动体直径和轴承节径。

然后根据轴承缺陷的振动机理,对轴承的非线性接触力进行分析。首先根据赫兹接触力公式,可以计算得到滚动体与轴承内外圈的接触力:

(3)

式中:fj代表第j个滚动体和内外圈壁之间的接触力,kb代表滚动体的刚度值,δj代表第j个滚动体的形变量。本文中,研究对象为6205深沟球轴承,滚动体的个数应该为9个,即j的取值应该为1～9之间的整数。

根据每个滚动体的角度位置,以及内外圈的动力学简化得的4个自由度上的位置,可以得到每个滚动体的形变量:

δj=(xs-xp)cosφj+(ys-yp)sinφj

(4)

式中:φj为第j个滚动体的角度位置。φj的值可以由式(5)求得:

(5)

该式从几何的角度,交代了每个滚动体在t时刻的角度位置。其中,ωc表示保持架的角速度,该角速度可以由与内圈相连的传动轴的角速度得到:

(6)

根据式(9)～式(12)可以求得每一个滚动体的接触力,再通过角度关系将赫兹力进行分解,将其分为水平和竖直两个方向。

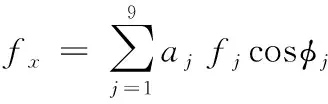
(7)

由于变形量为负数时,赫兹力计算值为负数,实际滚动体和内外圈壁并未接触。因此,引入aj将赫兹力计算值为负数的滚动体的值舍弃,即:

(8)

即表示只有当δj>0时,第j个滚动体的赫兹力才被记入。

2 构建深沟球轴承孪生体模型

根据第1节对深沟球轴承的动力学分析,本章将搭建孪生体模型。搭建孪生体模型使用软件为MWork.Sysplorer,开发语言为Modelica多领域建模语言,计算机硬件配置为Intel(R) Core(TM) i5-10400F CPU@2.90 GHz,16 G内存。

根据动力学分析结果,依次构建轴承的健康状态、外圈缺陷故障和内圈缺陷故障3种状态的孪生体模型。6205深沟球轴承的基本参数如表1所示。

表1 6205深沟球轴承基本尺寸 (mm)

根据以上基本参数,以及前第1节中的动力学分析,构建待测轴承的孪生体模型。

在搭建待测轴承的孪生体基础上,利用modelica语言可以呈现真实物理拓扑结构的优势,继续搭建整个振动信号测试系统的孪生体。由于轴承在运行时,其运动状态主要受载荷以及得到的转速影响。在实际测量过程中,由于加速度计测得结果会受测量误差、不可控环境因素等影响,在系统中加入一组符合高斯分布的随机数。为了更加真实地表现出轴承实际运动的状态,引入以下3个模块:载荷传递模块、转速传递模块以及测量误差载入模块。最终搭建起的孪生体模型结构如图2所示。

图2 6205深沟球轴承测试系统孪生体

在该系统中,轴承接收到由轴传递的转速和载荷,引起了轴承的运动,这个过程产生了振动,由于测量的误差导致测量值与真实值存在随机误差,最终由加速度计得到轴承的振动信号。

3 实验验证及结果分析

本章对数字孪生模型的仿真准确度进行了实验验证。对相同健康状态下的数字孪生模型仿真信号、实测信号以及理论信号3组振动信号的故障特征频率进行比较,验证数字孪生模型的准确度。

首先,通过孪生体模型得到轴承的仿真振动信号,利用傅里叶变换得到其故障特征频率;其次,使用某大学的轴承故障数据中心的数据作为实测信号,利用傅里叶变换得到其故障特征频率;然后,根据式(2)计算得到的理论故障特征频率。

用仿真信号的故障特征频率分别与另外两组信号的故障特征频率对比,得到相对误差,验证搭建的数字孪生模型的准确率。

某大学的试验台使用轴承型号为SKF6205深沟球轴承。设定电机转速为1750 rpm,选取的采样频率为12 kHz,采样点数为8192,健康状态为内圈故障、外圈故障以及正常轴承3类。

3.1 内圈故障状态下结果分析

根据式(2)以及表1可以计算的到,在内圈故障的状态下,轴承的故障特征频率为157.94 Hz。

由于某大学数据为实际测量得到,在对其进行分析之前,需要首先对原数据进行降噪处理。使用希尔伯特变换对原始信号进行包络,去除大量无用的高频噪音,得到实测振动信号。

由图3和图4可以得到,在测试台上实际测量得到的内圈故障轴承振动信号,其故障频率为158 Hz。

图3 实测内圈故障振动信号时域图 图4 实测内圈故障振动信号频域图

随后,对数字孪生模型进行状态设置,设定转速为1750 rpm,选取的采样频率为12 kHz,仿真时长为1 s,故障类型为内圈故障,缺陷尺寸为0.001 608 m。仿真后得到振动信号,如图5所示。

图5 仿真内圈故障振动信号时域图 图6 仿真内圈故障振动信号频域图

由图5和图6可以得到,通过对数字孪生体仿真得到的内圈故障轴承振动信号,其故障频率为157.89 Hz。

根据以上实验结果可知,仿真信号与理论值误差率为0.037%,仿真信号与实际测量值误差率为0.07%。由此可知,数字孪生模型在内圈故障状态下能够较准确地表现轴承的运动特征,符合轴承在内圈故障状态下的运动规律。

3.2 外圈故障状态下结果分析

根据式(2)以及表1可以计算得到,在外圈故障的状态下,轴承的故障特征频率为104.55 Hz。在对实测振动信号进行分析前对原数据进行降噪处理,避免原信号中的大量高频噪音影响结果分析。

由图7和图8可以得到,在测试台上实际测量得到的外圈故障轴承振动信号,其故障频率为105 Hz。

图7 实测外圈故障振动信号时域图 图8 实测外圈故障振动信号频域图

随后,对数字孪生模型进行状态设置,设定转速为1750 rpm,选取的采样频率为12 kHz,仿真时长为1 s,故障类型为外圈故障,缺陷尺寸为0.001 608 m。仿真后得到振动信号,如图9所示。

图9 仿真外圈故障振动信号时域图 图10 仿真外圈故障振动信号频域图

由图9和图10可以得到,通过对数字孪生体仿真得到的外圈故障轴承振动信号,其故障频率为104.59 Hz。

根据以上实验结果可知,仿真信号与理论值误差率为0.038%,仿真信号与实际测量值误差率为3%。由此可知,数字孪生模型在外圈故障状态下能够较准确地表现轴承的运动特征,符合轴承在外圈故障状态下的运动规律。

4 结束语

利用多领域建模语言Modelica建立了滚动轴承测试台的数字孪生模型。对数字孪生模型仿真的到不同健康状态轴承的振动信号,将其与实测振动信号以及理论计算值相比较,验证数字孪生模型的准确性。结果表明该模型能够准确地表现轴承的健康状态,可以检测轴承的运行状态。