基于改进MRAS算法的转动惯量辨识策略*

尚诚诚,赵 云,曹颖强,万翔宇

(湖北工业大学电气与电子工程学院,武汉 430068)

0 引言

伺服系统是一类能够自动的按照给定信号的变化调整系统的输出,达到与信号给定快速、精确跟随的自动控制系统,交流伺服技术是研制开发各种先进的机电一体化设备的关键性技术。伺服系统中永磁同步电机(permanent magnet synchronous motor,PMSM)的负载转动惯量变化将会影响其速度响应特性,进而影响其机械特性。因此,快速准确的辨识转动惯量,对提升PMSM调速系统的动态性能意义重大[1-2]。

目前,针对PMSM的转动惯量辨识研究,主要分为离线辨识和在线辨识两种类别,离线辨识是在电机工作之前完成对电机参数的测量,其易于实现但是无法实时获取电机的参数信息,并且辨识精度不高,适用于固定工况且低性能要求的工业场合[3-6];在线辨识可以在电机运行过程中实时获取电机参数,其主要方法有扩展卡尔曼滤波法(extended kalman filter,EKF)、递归最小二乘法(recursive least squares,RLS)、模型参考自适应算法(model reference adaptive system,MRAS)和状态观测器法等[7-11]。朱雅等[12]提出了基于级联 MRAS的PMSM参数在线辨识算法,该方法有效解决了多参数辨识中的欠秩问题。王飞宇等[13]提出了一种改进的基于MRAS的转动惯量辨识方法,其方法依据辨识参数偏差而实时改变的变增益系数,提高了辨识精度但抗干扰性差,且设置的参数评价函数增加了计算量。董烈超等[14]提出了变增益模型参考自适应辨识法(MRAS),设计了MRAS的增益的自适应律,并通过遗传算法对控制参数进行优化,提高了系统的动态性能,但辨识精度有待改善。

本文通过分析MRAS系统中自适应增益系数对PMSM转动惯量的辨识速度与辨识稳定性的影响,设计出了针对收敛速度与稳定性的评价函数,并以此提出了一种基于改进的MRAS增益的自适应控制律,通过仿真得出该方法具有收敛速度快,稳定性高等优点。

1 电机数学模型和MRAS辨识方法

1.1 电机数学模型

永磁同步电机的数学模型建立在不计涡流损耗、磁滞损耗和忽略铁芯饱和等条件下,采用了id=0的矢量控制方法,表贴式PMSM的Ld=Lq,因此电机的数学模型可简化为:

(1)

式中:ψd、ψq分别是永磁同步电机变换到直轴和交轴上的磁链,ωe是电机电角速度,Rs是永磁同步电机定子电阻,iq为三相电流等效在交轴上的电流,ud、uq分别是三相电流等效在永磁同步电机直轴和交轴上的电压,J是永磁同步电机转动惯量和负载惯量之和,ωm是电机机械角速度,Te是永磁同步电机电磁转矩,TL是永磁同步电机负载转矩,B是永磁同步电机的粘滞摩擦系数,ψf是永磁体磁链,np是永磁同步电机的极对数。

1.2 模型参考自适应辨识算法

对伺服系统的机械运动方程采用后向差分法进行离散化处理,得到k时刻的机械角速度表达式为:

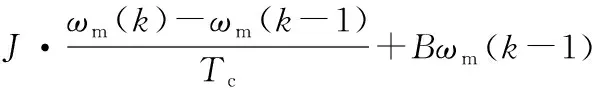
(2)

式中:Tc为模型参考自适应系统的采样周期。

同理可得k-1时刻的机械角速度表达式,式(2)与之相减可得:

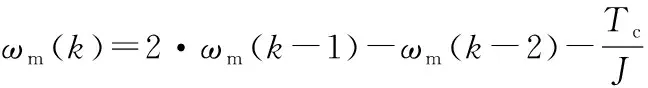
(3)

在转动惯量的辨识算法中,由于转速的采样频率很高,因此可把负载转矩视为常数,即:TL(k-1)=TL(k-2),将其带入式(3)可得:

ωm(k)=2ωm(k-1)-ωm(k-2)+b·Δ

(4)

式中:

b=Tc/J
Δ=B(ωm(k-2)-ωm(k-1))+Te(k-1)-Te(k-2)

将式(4)作为参考模型,由模型参考自适应算法原理得可调模型为:

(5)

(6)

则可由式(4)～式(6)推得转动惯量的自适应辨识律为:

(7)

式中:β为辨识增益系数。MRAS控制结构框图,如图1所示。

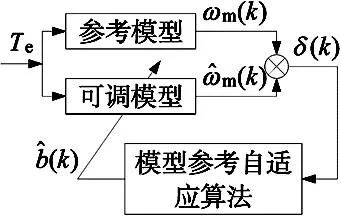
图1 MRAS控制框图

2 辨识增益自适应调整算法

在基于MRAS的转动惯量辨识中,辨识增益β是决定辨识效果的关键性参数,辨识增益β的变化将导致辨识过程中辨识速度与辨识波动性的变化。β越小,辨识波动性越小,稳定性越好,辨识速度越慢;β越大,辨识波动性越大,稳定性越差,辨识速度越快。

目前基于MRAS的转动惯量辨识中,对于β的选择需要根据经验人为选择,并且很难同时满足快速性与稳定性的需求,本研究为解决此问题,建立了辨识增益与当前辨识结果之间的关系,设计评价函数,实现了辨识增益β的自适应调整。

自适应增益方法推导:设当前辨识周期与上一个辨识周期的辨识结果差值为:

Δ(J)=|J(i)-J(i+1)|

(8)

则定义评价函数P:

(9)

式中:h为放大系数,T为采样时间,Tc为模型参考自适应算法的采样周期,定义评价函数判定常数D。

则辨识增益β的自适应控制律为:

β=β0+S

(10)

式中:β0为初始增益,S是一个随采样周期增大的正比例函数信号。

在每个辨识周期中,评价函数P的计算结果与评价函数判定常数D进行比较,当评价函数P满足判定条件D时,辨识增益β将进行自适应变化以更新辨识增益的值。当辨识增益β不满足判定条件条件时,辨识增益停止更新。

辨识增益自适应变化流程图与参数辨识原理图,如图2所示。

(a) 辨识增益自适应变化流程图 (b) 参数辨识原理图图2 辨识增益自适应变化流程图和参数辨识原理图

3 仿真验证分析

3.1 系统搭建与实验条件

基于MATLAB/Simulink搭建仿真模型,仿真条件为:转速指令设定1500 r/min,在t=0 s时加入为恒定负载,设定PMSM转动惯量在t=0.2 s时从0.008 kg·m2阶跃至0.009 kg·m2。转动惯量辨识系统仿真图和变增益模型参考自适应子模块分别如图3和图4所示。

图3 转动惯量辨识系统仿真

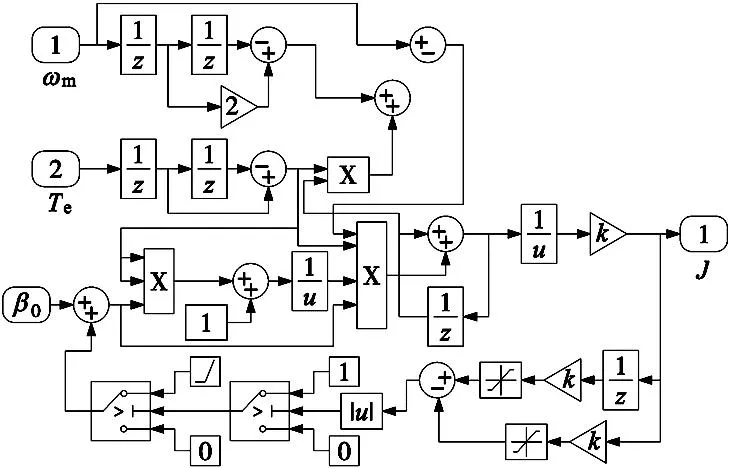
图4 变增益模型参考自适应子模块

所选用永磁同步电机参数如表1所示。

表1 电机参数表

3.2 自适应增益β的选择对辨识结果的影响

取辨识增益为β=0.1,β=0.5,β=50,β=100,使用固定增益MRAS对PMSM的转动惯量进行辨识,仿真结果如图5所示。

(a) 不同增益下MRAS法的转动惯量辨识波形 (b) 辨识波形局部放大图图5 不同增益下MRAS法的转动惯量辨识波形

由图5可知,在β=0.1时,转动惯量阶跃变化前收敛时间为0.125 s,阶跃变化后收敛时间为0.1 s;在β=0.5时,转动惯量阶跃变化前收敛时间为0.04 s,阶跃变化后收敛时间为0.02 s;在β=50时,转动惯量阶跃变化前收敛时间为0.002 s,阶跃变化后收敛时间为0.002 s;在β=100时,转动惯量阶跃变化前收敛时间为0.001 9 s,阶跃变化后收敛时间为0.001 9 s。因此可以看出,自适应增益β的值越大,转动惯量辨识波形的收敛速度就越快,但β大到一定程度后,对收敛速度的影响也随之减弱。同时可以看出,β的值越大,转动惯量辨识波形的振动幅度也越大。

3.3 变增益MRAS转动惯量辨识仿真

使用变增益MRAS转动惯量辨识方法进行转动惯量辨识仿真,同时选择β=0.1与β=50时的固定增益辨识波形进行对比,所得波形如图6所示。

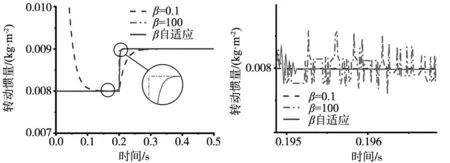
(a) 变增益与固定增益辨识对比波形图 (b) 辨识波形局部放大图图6 变增益与固定增益辨识对比波形图

由图6可知,变增益MARS转动惯量辨识在转动惯量阶跃变化前收敛时间为0.001 s,阶跃变化后收敛时间为0.011 s。因此可以看出,在辨识初始阶段,变增益MRAS的收敛速度较快,在转动惯量阶跃后,也能进行快速追踪辨识。相比于固定增益MRAS的辨识,变增益MRAS辨识在辨识完成后,其辨识波形能快速达到稳定,振动幅度显著降低。变增益MRAS转动惯量辨识在收敛速度和波动性上都具有较好的表现,该方法具有收敛速度快,辨识波动性小,抗扰动性好的优点。

4 结论

本文在传统的固定增益MRAS的基础上,提出了一种改进的变增益MRAS转动惯量辨识方法,并通过仿真软件搭建模型,进行了仿真验证和分析,证明了该方法的可行性。

变增益MRAS法改善了传统MRAS的辨识增益系数需求人为选择的缺点,实验结果显示:在收敛速度方面,变增益MRAS的转动惯量辨识收敛速度比固定增益MRAS的收敛速度快;在稳定性方面,变增益MRAS的转动惯量辨识收敛速度比固定增益MRAS的振动幅度小,并在辨识波形收敛后快速达到稳定。因此,变增益MRAS法可同时拥有收敛速度快和辨识稳定性高两方面的优势,具有辨识速度快、抑制参数辨识振荡、辨识精度高的特点。