时变输出约束机械臂系统渐近跟踪控制*
常太群,赵 林
(青岛大学自动化学院,青岛 266071)
0 引言
机械臂系统由于其具有精度高、安全性高、效率高、适用范围广等特性,在工业生产中得到了广泛应用[1]。机械臂的跟踪控制问题是一个重要的研究领域,为了确保机器人手臂的安全、准确和高效的运动,学者们提出了许多控制方法如滑模控制[2]、自适应控制[3]和H∞控制[4]等。近年来,反步法已成为解决这一问题的有效的方法之一[5]。然而,传统反步法中由于虚拟信号的重复微分引起的“计算爆炸”问题会影响系统的控制性能。DONG等[6]提出了命令滤波反步方法解决了“计算爆炸”问题,并通过引入误差补偿机制来消除滤波误差,提高了系统的控制精度。注意到在上述研究中,跟踪误差仅仅收敛到原点附近的小邻域内,并不能保证系统状态与期望信号之间的跟踪误差渐近收敛到零[7]。因此研究机械臂系统的渐近跟踪控制是十分必要的。
另一方面,具有输出约束的机械臂系统在各个行业中都有广泛的应用,通过限制机械臂系统的输出,更好地控制其位置和速度,这对于需要进行高精度操作的应用非常重要。HE等[8]将障碍李雅普诺夫函数应用于具有输入死区和输出约束的机械臂来解决其跟踪问题。此外,机械臂常常用于复杂环境中执行任务。这些环境中可能存在非对称时变状态约束,例如摩擦、振动或负载变化。这对于具有输出时变约束的机械臂系统的跟踪控制提出了更高的要求。SI、YU等[9-10]分别研究了随机非线性系统和严格反馈非线性系统的非对称时变全状态约束。除此之外,上述文献所采用的时间触发控制(TTC)任务的周期性执行会导致通信资源浪费。XING等[11]提出的事件触发控制(ETC)策略可以通过减少控制器更新频率节省通信资源。在LI等[12]中,作者将事件触发控制协议和有限时间控制应用于具有输出约束的机械臂系统。
在此基础上,本文提出了一种事件触发自适应渐近控制算法来解决时变不对称输出约束机械臂系统的跟踪问题。主要贡献如下:
(1)采用命令滤波反步法消除了滤波误差,避免了“计算爆炸”问题。同时,利用时变障碍李雅普诺夫函数保证了机械臂系统的输出都在预设的非对称时变约束内,提高了机械臂系统的控制性能。
(2)借助新的时变阈值的事件触发控制协议和时变技术,设计了一种新的事件触发控制器来补偿残差项,最终保证跟踪误差渐近收敛于零。同时,节约了机械臂系统的通信资源。
1 控制问题描述
考虑如下具有不匹配扰动的机械臂系统的动力学方程:
(1)
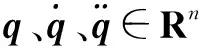
为方便起见,定义新变量如下所示:
(2)
式(1)可以写为:
(3)
式中:y∈Rn为机械臂系统的输出。
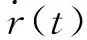
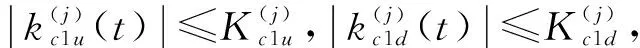
本文的控制目标是设计一个控制器u,使其满足以下条件:①系统输出y能实现渐近跟踪期望信号r(t);②闭环系统中的所有信号都是有界的;③系统输出y被限制在时变紧集Φ中,其中Φx={x∈Rn,kc1d(t)
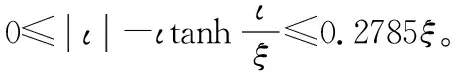
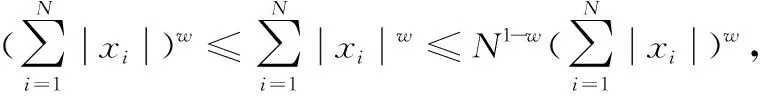
式中:ps是正常数。
关于式(1)中的动力学模型,存在如下性质:
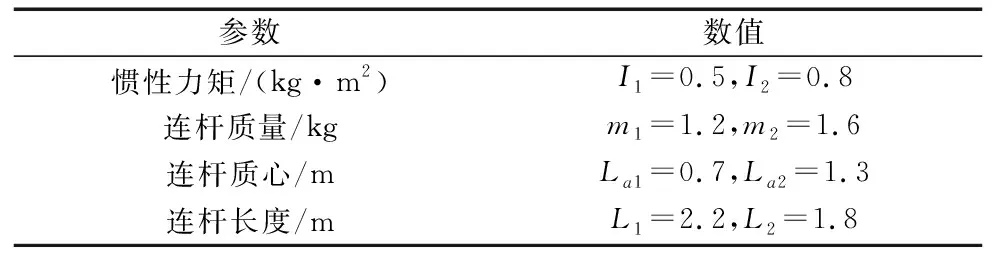
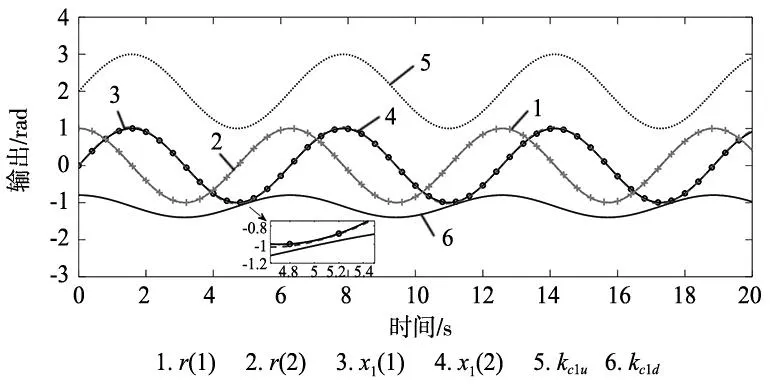
性质1:存在两个正常数g1和g2满足以下条件0 首先,选取命令滤波器,其描述如下: (4) 式中:如果输入信号及其导数是有界的,并且π1(0)=α1(0),π2(0)=0,则对于ω>0,Ωn>0,0<ζ≤1,存在|π1-α1|≤ω。 定义坐标变换如下: (5) 式中:z1,z2表示跟踪误差,π1表示滤波器输出,Ξ1表示误差补偿信号。 虚拟控制信号、误差补偿信号和自适应律设计为: (6) 第一步:对于补偿后的跟踪误差c1,选取时变障碍李雅普诺夫函数为: (7) 定义时变不对称约束为: (8) 式(7)可以转换为式(9)中的形式: (9) 对式(9)求导得: (10) 注意到: (11) 把式(6)代入到式(10),可以得到: (12) 第二步:选取李雅普诺夫函数为: (13) 对式(13)求导得到: (14) 受文献[16]启发,将新的事件触发控制协议定义为: (15) 式中:ws(t)=vs(t)-us(t),0≤δ1<1,δ2和ε是正常数。 根据事件触发控制协议,将控制器设计为: (16) 连续控制信号设计如下: (17) 式中:λ1(t),λ2(t)∈[-1,1]是设计的时变参数。 所以,可以得到: (18) 由杨氏不等式和引理1,上式可以写成: (19) (20) 将式(18)~式(20)代入式(14)可以得到: (21) (22) 对于满足假设1、假设2和假设3的机械臂系统,如果命令滤波器、虚拟控制信号、误差补偿信号、自适应更新律和事件触发协议设计为式(6)和式(15),则跟踪误差将渐近收敛于零且系统的输出满足非对称时变约束。同时,可以成功地排除Zeno行为。 首先,构造误差补偿信号的李雅普诺夫函数: (23) 对式(23)求导得: (24) 因为不等式|π1-α1,s|≤ω1,其中ω1是一个正常数,通过设计ω1 (25) 构造全局李雅普诺夫函数: (26) 对其求导得到: (27) 将式(6)、式(22)、式(25)代入式(27)得: (28) 根据杨氏不等式,放缩后得: (29) 非对称时变约束证明: 渐近跟踪证明: 根据引理3,式(29)可进行如下放缩: (30) 对式(30)在[t0,t)积分得: (31) (32) (33) (34) 根据Barbalat引理可知: (35) 最终,证明了该机械臂系统可以实现渐近跟踪即跟踪误差渐近收敛到零。 Zeno行为证明: 为了验证所提出算法的有效性,我们考虑如下二自由度机械臂系统,并利用MATLAB软件进行仿真分析。机械臂参数如表1所示。 表1 机械臂动力学参数 定义惯性矩阵为: 定义科里奥利向心矩阵为: 通过仿真得到响应曲线如图1~图3所示。由图1a可知,在具有非对称时变约束的事件触发自适应渐近跟踪控制算法(EBAFATC)下,机械臂系统的输出能够精确地跟踪期望信号。同时,在相同参数选择下,对比图1b中的不具有非对称时变约束的算法(EBAFATCWO),图1a中机械臂系统的输出不会违反非对称时变输出约束,而图1b中超出了限制,验证了本文所提算法的有效性。图2展示了EBAFATC算法和没有渐近跟踪控制算法(EBAC)的qδ=|q1-r1|+|q2-r2|曲线的对比,其中图2a~图2d中的扰动大小分别为: (a) EBAFATC算法 d1=[0.2sin(t),0.2cos(t)]T,d2=[3sin(t),3cos(t)]T, 可以看出,保持所有参数相同仅改变扰动大小,EBAFATC比EBAC具有更好的控制精度和鲁棒性,即使失配扰动增大,qδ仍能渐近收敛于零。图3展示了控制器执行间隔,Zeno行为被成功避免。根据表2可以得到,控制器触发次数明显减少,EBAAC算法可以节约通信资源,减少通信负担。 (a) u1触发事件间隔 (b) u2触发事件间隔图3 EBAFATC控制器触发事件间隔 表2 ETC和TTC对比结果 本研究提出了一种事件触发自适应渐近跟踪控制方法来解决非对称时变约束下机械臂系统的跟踪问题。借助命令滤波反步法,一方面成功地避免了“计算爆炸”问题,另一方面通过引入误差补偿系统消除了滤波器产生的误差。此外,提出了一种新的事件触发控制策略,为机械臂系统节省了通信资源。基于时变技术,机械臂系统的跟踪误差能够渐近收敛到零,并且其输出在非对称时变约束内,使得其能够适应复杂多变的实际工程环境中,具有广阔的应用前景。最后,通过仿真验证了该方法的有效性和可行性。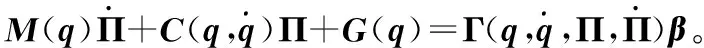

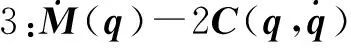
2 自适应命令滤波反步法控制器设计
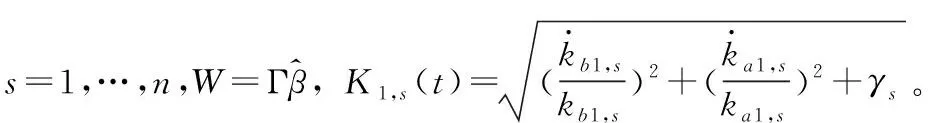

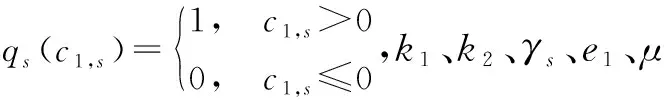
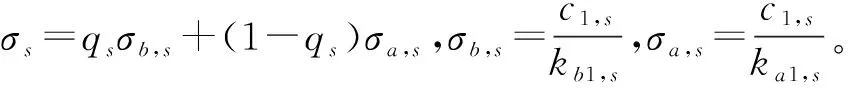
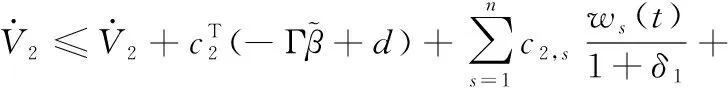
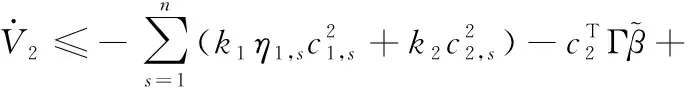
3 稳定性分析
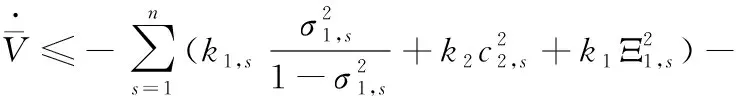
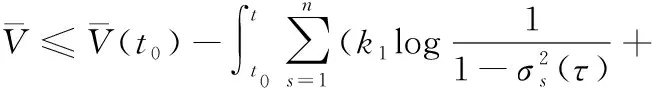
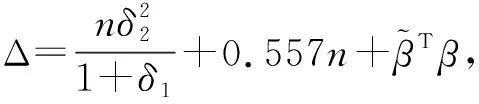
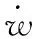
4 仿真结果与分析
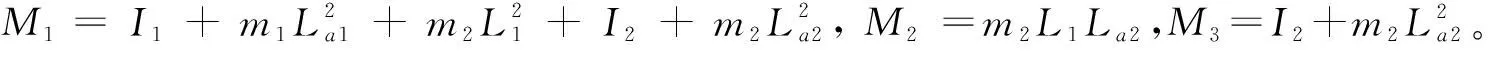
d3=[30sin(t),30cos(t)]T,d4=[150sin(t),150cos(t)]T。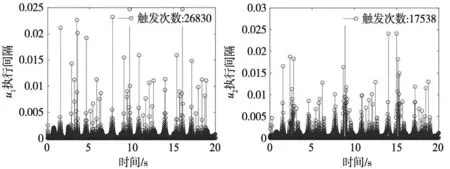

5 结论

