采用激励轨迹实现机器人关节伺服动刚度的辨识*

潘海鸿,陈 韬,贾丙琪,孙仲鸣,丁可帅,陈 琳

(广西大学机械工程学院,南宁 530004)

0 引言

工业机器人在运动过程中惯量变化、耦合及非线性干扰等都会对伺服驱动系统产生扰动,进而影响机器人轨迹精度。伺服动刚度是评价伺服驱动系统抵抗外界动态扰动能力的一个重要指标,因而获得更高精度的实际驱动系统伺服动刚度并在此基础上进行进一步研究具有重要意义。

尹明、陈彦羽等[1-2]通过建立伺服驱动系统的简化数学模型来计算伺服动刚度,但其仅用于仿真研究伺服动刚度的影响因素。ALTER等[3]给被测电机加载正弦负载力,正弦负载力下的幅值和稳态位移偏差幅值的比值为该频率下的伺服动刚度,变换正弦负载力加载频率就得到关于不同频率下的伺服动刚度,但该力矩加载方法不适于实际工程测试。卢少武、MA等[4-5]在进行实际测量分析时,采用突然卸载重物负载来模拟阶跃力来辨识伺服动刚度。为方便叙述,依据其特征可将其命名为阶跃力法。阶跃力法是将阶跃负载力幅值与位置跟踪误差最大值的比值作为伺服动刚度,但与严格意义上伺服动刚度的一般定义不符[6]。且阶跃力法应用于实际工业机器人(特别是重载工业机器人)伺服动刚度辨识时,频繁撤去负载的操作会产生安全问题。

为此提出一种采用激励轨迹来辨识工业机器人伺服动刚度的方法,将其命名为轨迹法。轨迹法以五阶傅里叶级数轨迹为激励轨迹,通过最小二乘法对采集的数据进行计算拟合获得机器人关节伺服动刚度和动力学模型参数,并基于此计算关节扰动力矩。通过比对使用轨迹法和阶跃力法所辨识的伺服动刚度下的扰动力矩补偿效果来评判两种辨识方法结果的精度。在工业机器人实验平台上验证实验结果表明轨迹法辨识所得伺服动刚度的精度优于阶跃力法。

1 轨迹法辨识原理及步骤

由伺服动刚度的定义可知,伺服动刚度等于动态扰动力矩和扰动力矩所引起的位置跟踪误差的比值,而电机实际力矩和位置跟踪误差是由输入信号和扰动力矩共同作用在控制器上产生的,需对二者进行处理提取动态扰动力矩和动态扰动力矩引起的位置跟踪误差来计算伺服动刚度的大小。轨迹法采用式(1)所示五阶傅里叶级数轨迹作为激励轨迹,通过设置基础频率ωf的大小来确保理论轨迹的频率避开扰动力矩的频率区间,且高通滤波器截止频率应大于激励轨迹频率,进而可滤除理论轨迹对伺服驱动器实际位置跟踪误差和电机力矩的影响,高通滤波后的位置跟踪误差和电机力矩仅与扰动力矩有关。

(1)

式中:ai,0、ai,k、bi,k(k=1,2,…,5)为常数项,qi(t)为工业机器人第i关节轨迹,ωf为基础频率。

可通过研究扰动力矩与位置跟踪误差、电机力矩之间的关系,来提取扰动力矩及其所产生的位置跟踪误差。电机实际位置跟踪误差Δθ为输入信号和扰动力矩共同作用在控制器上产生。

(2)

式中:G1(s)为伺服系统简化模型,G2(s)为被控对象简化模型,θref为理论输入位置指令,Tdis为扰动力矩,Tm为电机实际力矩。对位置跟踪误差Δθ进行高通滤波,滤除理论轨迹的影响,滤波后的位置跟踪误差可视为扰动力矩所引起的位置跟踪误差Δθ1。

电机实际力矩Tm也为输入信号和扰动力矩共同作用在控制器上产生。

(3)

通过设置合理的伺服驱动器控制参数能满足无扰动Tdis(s)下的位置跟踪误差Δθ2(s)≈0,即满足G1(s)G2(s)≫1,则式(3)可简化成:

(4)

对实际电机力矩Tm通过高通滤波器去除输入信号的影响后的力矩也可认为是扰动力矩Tdis。

经以上分析,轨迹法可按以下步骤辨识工业机器人关节伺服动刚度:

步骤1:确定五阶傅里叶级数的基频ωf,保证理论轨迹频率避开扰动频率区间,并综合考虑机器人动力学参数辨识对轨迹的约束要求[9]来设计最优激励轨迹;

步骤2:运行五阶傅里叶级数轨迹,实时采集电机实际位置跟踪误差和实际力矩;

步骤3:对实际位置跟踪误差和实际力矩进行高通滤波,截止频率应大于激励轨迹最高频率,通过滤波获得伺服系统扰动力矩Tdis和产生的位置跟踪误差Δθ1;

步骤4:采用最小二乘法计算刚度K大小:

(5)

2 伺服驱动器扰动力矩模型

2.1 基于伺服动刚度和动力学模型的扰动力矩模型

(6)

图1 扰动力矩补偿控制器原理框图

图2 六自由度工业机器人实验平台

2.2 机器人动力学模型及参数辨识

伺服动刚度扰动力矩模型中所用的机器人动力学模型可通过动力学参数辨识获得。将机器人关节摩擦力模型简化为库伦+粘滞摩擦模型[7],可建立机器人的线性化动力学模型,并进一步推导出机器人只包含最小惯性参数的动力学模型[8]:

(7)

采用分步辨识的辨识策略:先固定5、6轴,1、2、3、4轴运行激励轨迹,辨识获得1、2、3轴最小惯性参数;再固定2、3轴,运动1、4、5、6轴运行激励轨迹,获得4、5、6轴最小惯性参数;辨识完成后六轴同步运行验证轨迹,验证辨识模型的精度。

3 实验

3.1 实验平台及实验方案

搭建六自由度工业机器人实验平台主要包括RTX运动控制器、电气控制柜以及实验室自主搭建的型号为GXU-W6R的工业机器人机械本体等。控制器数据下发周期和采样周期均设置为1 ms。自主搭建的工业机器人采用松下A6系列EtherCAT驱动器及配套电机,可实现力矩实时补偿。

在工业机器人实验平台上分别进行以下实验:

(1)辨识工业机器人动力学模型并分别采用阶跃力法和轨迹法辨识获得6个关节伺服刚度;

(2)分别采用阶跃力法和轨迹法所获伺服动刚度进行机器人单关节伺服动刚度验证实验,对比验证轨迹法所得伺服动刚度的精度优于阶跃力法;

(3)进行轨迹法辨识关节伺服动刚度在工业机器人6个关节上的验证实验,验证轨迹法辨识所得机器人关节伺服动刚度的精度。

3.2 动力学模型和关节伺服刚度辨识实验

激励轨迹的基频设为0.1 Hz,计算获得最优激励轨迹,关节伺服动刚度所用高通滤波器截止频率设为1 Hz。机器人分别运行图3a所示1、2、3、4轴激励轨迹和图3b所示1、4、5、6轴激励轨迹,辨识获得机器人动力学模型和各个关节伺服动刚度Km;并通过阶跃力法获得机器人各个关节伺服动刚度KL。

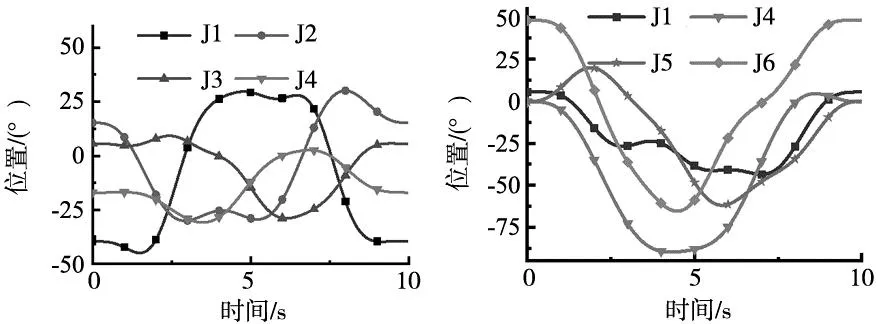
(a) 1、2、3、4轴激励轨迹 (b) 1、4、5、6轴激励轨迹图3 机器人激励轨迹

运行图4机器人动力学模型验证轨迹,对比计算力矩与实际电机力矩来验证动力学模型的精度,验证结果见图5,机器人前3关节辨识模型计算力矩与关节实际力矩拟合程度较好,辨识精度整体高。但在低速段和速度换向处辨识精度较差,其原因仍然是在换向处和低速段库伦+粘滞摩擦模型无法预测真实关节摩擦力。后3关节为小惯量轴,最小二乘法仅考虑整体误差,计算时会导致小惯量轴误差较大,且第5、6关节间存在耦合现象,导致后3关节(尤其是第6关节)相对于前3关节辨识精度较差。由表1可知各关节模型计算力矩误差残差均方根和极值的绝对值都比较小,也验证了动力学模型辨识结果的精度。

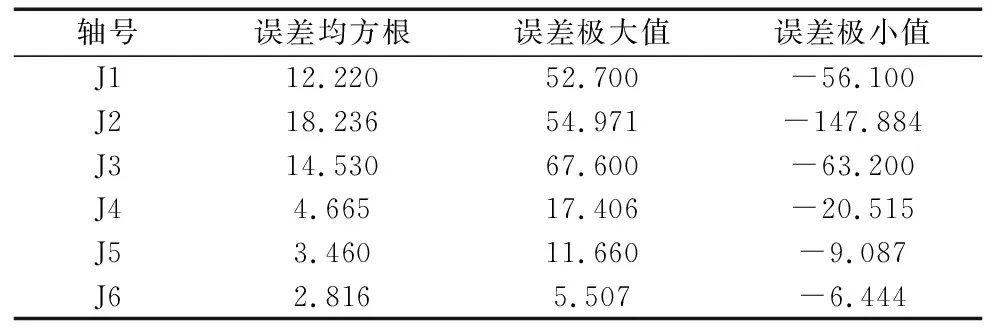
表1 机器人各关节模型计算力矩误差 (N·m)

图4 机器人动力学模型验证轨迹

阶跃力法辨识伺服动刚度KL与轨迹法辨识伺服动刚度Km如表2所示。表2中各个关节KL普遍大于Km,是由于末端施加阶跃力矩传递到电机过程中存在摩擦和弹性力矩的损耗,导致电机末端所受力矩数值变化小于阶跃力矩数值变化,使得阶跃力法计算所用力矩大于新辨识法所用力矩,而位置跟踪误差均采用电机位置跟踪误差,导致理论上阶跃力法所得刚度会大于运动辨识法所得刚度。

3.3 单关节伺服动刚度验证实验

单关节运动轨迹下进行验证实验,机器人第2关节运行图6a轨迹,在机器人动力学模型保持不变的基础上改变伺服动刚度系数进行对比验证实验:①无力矩补偿;②取关节伺服动刚度为0时(记为K0)时,进行扰动力矩补偿实验,扰动力矩补偿实验方案如图7所示;③取关节伺服动刚度为阶跃力法所辨识伺服动刚度KL,进行扰动力矩补偿测试;④取关节伺服动刚度为轨迹法辨识伺服动刚度系数Km,进行扰动力矩补偿测试。

(a) 单关节验证轨迹 (b) 机器人6个关节验证轨迹图6 伺服动刚度验证实验轨迹

图7 伺服动刚度验证方法

其中①②组对比验证机器人动力学模型计算力矩补偿下的效果;②③④组实验中机器人动力学模型相同,仅伺服动刚度不同,理论上所使用的伺服动刚度值越接近于理论值,补偿后轨迹精度越高,可对比②③④组实验来验证KL和Km的精度优劣。

图8为单关节补偿对比图及局部放大图,表3中列出运动过程中位置跟踪误差振幅较大处的几组数据。由单轴补偿实验结果可以看出,相较于Δθ(K0),Δθ(KL)波动幅值明显加大,通过计算可得0.515～1.280 s内,Δθ(KL)/Δθ(K0)的均值为2.709,表明在该运动段Δθ(KL)波动幅值约远大于Δθ(K0)的波动幅值,采用KL进行扰动力矩补偿后轨迹精度明显变差;而Δθ(Km)/Δθ(K0)的均值为0.485,位置跟踪误差波动幅值下降51.5%,表明伺服动刚度系数Km明显优于Kh。在7.536～8.371 s内Δθ(KL)波动幅值也大于Δθ(K0)的波动幅值,Δθ(Km)/Δθ(K0)的均值为0.428,Δθ(Km)位置跟踪误差波动幅值较Δθ(K0)下降57.2%,表明伺服动刚度系数Km优于KL。综上所述,表明伺服动刚度Km比KL更接近理论值,进一步验证了轨迹法所得伺服动刚度的精度优于阶跃力法。

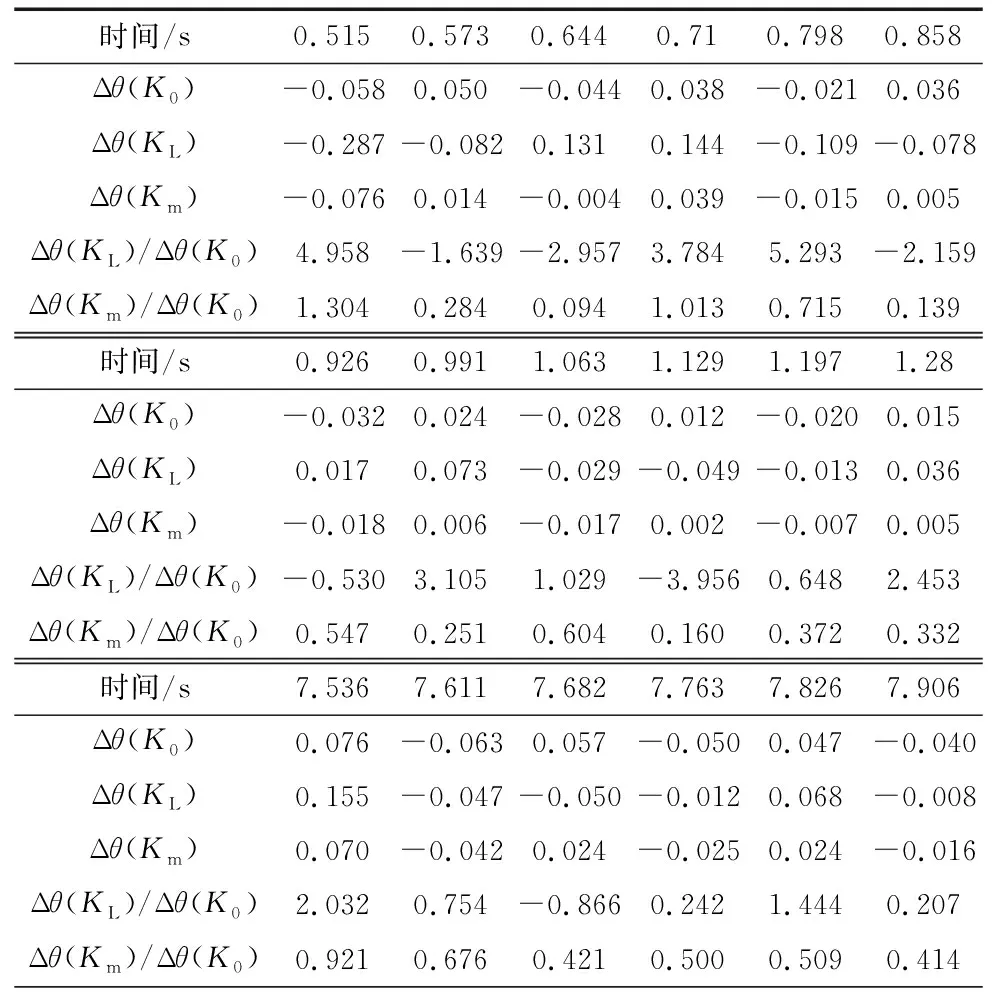
表3 不同时间、不同伺服动刚度系数下电机实际位置跟踪误差Δθ及比值(°)

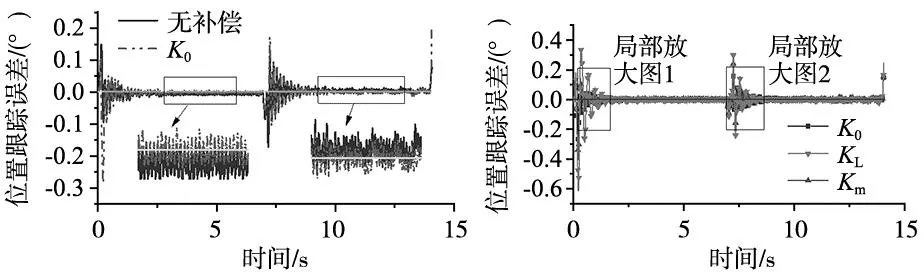
(a) 无补偿和K0补偿对比图 (b) 不同补偿系数补偿对比图

3.4 机器人6个关节伺服动刚度验证实验

工业机器人6个关节同步运行图6b轨迹,对比未补偿、各关节伺服动刚度为K0时的扰动补偿、各关节伺服动刚度为轨迹法所获伺服动刚度Km时的扰动补偿的实际位置跟踪误差。由于各关节伺服动刚度采用阶跃力法所获伺服动刚度KL进行扰动补偿时机器人产生严重抖动,无法进行正常测试,为设备安全起见,未继续进行KL下的扰动补偿测试。

机器人6个关节补偿前后各关节电机侧位置跟踪误差对比如图9所示,可以明显看到采用轨迹法辨识所得动刚度进行扰动力矩补偿时机器人运动精度得到明显改善,表明轨迹法能有效辨识出工业机器人的关节伺服动刚度。

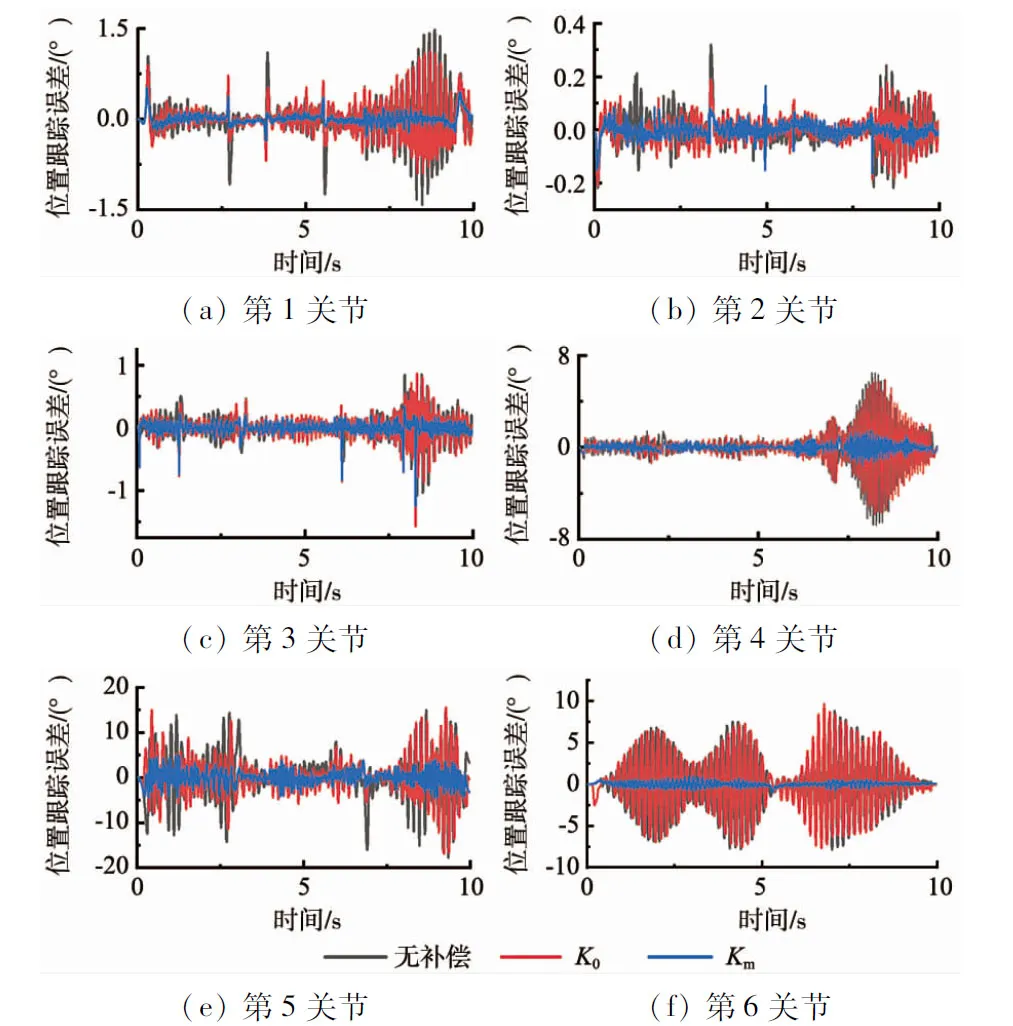
图9 机器人各关节电机侧位置跟踪误差

4 结论

为保证在安全的情况下获得更加精确的工业机器人伺服动刚度,提出一种采用激励轨迹进行工业机器人关节伺服动刚度辨识的方法。通过运行五阶傅里叶级数轨迹辨识获得机器人关节伺服动刚度和动力学模型,基于辨识结果计算扰动力矩并进行补偿,依据补偿后的位置跟踪误差来评判不同辨识方法辨识结果的优劣。在工业机器人单关节运动轨迹和6个关节运动轨迹下的验证实验结果均表明轨迹法所得动刚度的精度明显优于阶跃力法所得动刚度。