求锐角三角函数值的策略

郭跃龙

［摘 要］求锐角三角函数值是中考数学的必考点。文章结合五则典例，从五个方面对求锐角三角函数值的策略进行分析探讨，旨在丰富学生的解题经验，提高学生的核心素养。

［关键词］锐角；三角函数值；策略

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）29-0007-03

锐角三角函数值反映的是直角三角形中边与边的比，只有把锐角放在直角三角形中，才能让锐角三角函数值发挥作用。如何让不在直角三角形中的锐角放置在直角三角形中呢？常用方法包括垂线法、平移法、面积法、构造法等，通过这些方法可以实现等角转换，从而求得锐角三角函数值。

一、作垂线构造直角三角形

如果求锐角三角函数值的锐角不在直角三角形中，则常用的方法就是作垂线构造直角三角形，让这个锐角放置在直角三角形中，从而利用边与边的比求得锐角三角函数值。

点评：本题在求两个锐角的三角函数值时都分别作了垂线，构造了两个锐角所在的直角三角形，只需根据正切与正弦的定义求出边长。

二、作平行线平移角到直角三角形中

在网格中如果两条斜线在小正方形内相交成一个锐角，如何求这个锐角的三角函数值呢？常用的方法是作其中一条斜线的平行线，将这个锐角平移到一个直角三角形中，通过求直角三角形中锐角的三角函数值，得所求锐角的三角函数值。

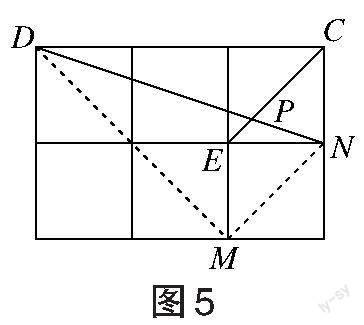
［例2］如图5所示，在边长为1的正方形网格中，连接格点D、N和E、C，DN和EC相交于点P，求[tan∠CPN]的值。

思考：求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形。观察发现：[∠CPN]不在直角三角形中，并且顶点不在格点处，则可以利用网格画平行线的方法解决此类问题，比如连接格点M、N，可得MN∥EC，则[∠DNM=∠CPN]，连接DM，那么[∠CPN]就变换到格点处，并且恰好在[Rt△DMN]中，可以方便求出[tan∠CPN]的值为                     。

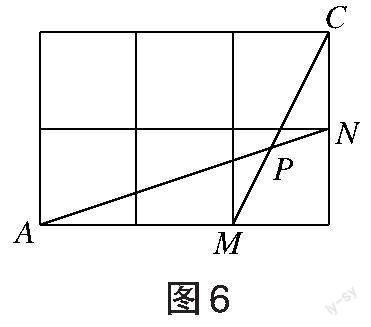
问题解决：（1）如图6所示，在边长为1的正方形网格中，AN与CM相交于点P，则[cos∠CPN]的值为               ；（2）如图7所示，在边长为1的正方形网格中，AN与CM相交于点P，则[sin∠CPA]的值为  。

思维拓展：如图8所示，若干个形状、大小完全相同的菱形组成网格，网格顶点称为格点，已知菱形的较小内角为60°，点A、B、C、D都在格点处，线段AB与CD相交于点P，求[cos∠CPA]的值。

解：如图9所示，∵[CE]∥[MN]，∴[∠MND=∠CPN]，∴[tan∠MND=tan∠CPN]，

问题解决：（1）如图10所示，取格点[Q]，连接[QM]和[CQ]。∵[CQ]∥[AN]，∴[∠CPN=∠QCM]，∵[△QCM]是等腰直角三角形，∴[∠CPN=

思维拓展：如图12所示，取格点E，连接EA、EB，设小菱形的边长为1，由题意可知：EA∥CD，∴[∠APC=∠BAE]，∵[∠AEO=60°]，[∠BEO=30°]，

点评：本题由易到难，由正方形网格到菱形网格，说明了作平行线平移角在网格中的应用。平移后的角的顶点必须是格点，所作平行线必须是连接格点形成的，网格可以延伸，可以作垂线辅助解答。

三、利用面积法求锐角三角函数值

在网格图中，通过作高构造直角三角形求锐角三角函数时，高线的长不能直接求得，此时应采用面积法求高线长，即用两种不同的方法表示同一个三角形的面积，建立方程求高线的长，从而求得锐角三角函数值。

［例3］如图13和图14所示，在[6×6]正方形方格纸中，每个小的正方形边长为单位1，点A、B、C、D都在格点处。（1）如图13所示，四边形ABCD的周长是。（2）如图14所示，AC与BD相交于点O，[tan∠BOC=]                    。

点评：在网格图中，端点不是格点的线段不易求得长度，影响求锐角三角函数值。本题提供了两种求这样线段的方法，一是相似三角形，二是面积法。

四、利用构造法求锐角三角函数值

所谓构造法就是构造图形，使用特殊角的三角函数值求非特殊角的三角函数值。

［例4］学校数学兴趣小组在尝试计算tan15°时，采用以下方法：如图16所示，在[Rt△ACB]中，[∠C=90°]，[∠ABC=30°]，延

解：如图17所示，在等腰[Rt△ABC]中，[∠C=90°]，延长CB至点D，使得[BD=AB]，则[∠BAD=∠D]。∵[∠ABC=45°=∠BAD+

五、利用三角函数公式求三角函数值

三角函数公式是指将两角和或差的三角函数转化为两个角的三角函数值的和或差，这本是高中阶段学习的内容。在初中阶段应用时，常以阅读材料的形式命题，通过定义新运算，要求学生应用三角函数公式求锐角三角函数值。

阅读材料，请选择适当的公式解答下列问题。（1）求sin75°；（2）如图18所示，边长为2的正[△ABC]沿直线滚动，设当[△ABC]滚动240°时，C点的位置在[C′]，当[△ABC]滚动480°时，A点的位置在[A′]。①求[tan∠CAC′]的值；②试确定[∠CAC′+∠CAA′]的度数。

点评：利用三角函数公式，可以利用特殊角的三角函数值求得非特殊角的三角函数值。本题求非特殊角的三角函数值时，也使用了作垂线的方法，说明作垂线求三角函数值仍是最基本的方法。

求銳角三角函数值的策略还包括对称法、全等转换法等，每一种策略都有其使用的条件，要根据不同的情境选择不同的策略。