齿轮箱传动系统渐开线花键的优化研究*
黄杨杨,宋进宇,罗勇水,赵海燕,祁广骞
(浙江运达风电股份有限公司 浙江省风力发电技术重点实验室,浙江 杭州 310012)
0 引 言
齿轮箱为风力发电机组传动链核心部件,其高可靠性和轻量化设计在目前风机价格竞争日益激烈的环境下显得尤为重要。
齿轮箱通常采用行星传动形式。目前,陆上主流双馈机组齿轮箱采用二级行星+一级平行或三级行星+一级平行的传动形式。采用三级行星+一级平行的传动结构,若齿轮箱行星轮轴承全为滚动轴承,则齿轮箱的扭矩密度达到200 kN·m/t以上才会具备市场竞争力。
花键是齿轮箱传动结构中至关重要的一种联接结构。齿轮箱中的花键联接主要用于太阳轮与行星架、太阳轮与低速中间轴之前的扭矩传递。花键联接一旦损坏,太阳轮无法正常浮动及传扭,齿轮箱增速功能失效,风机停机,无法正常服役发电。
目前,花键损坏后,维修人员无法在塔上进行维护,需更换整个齿轮箱。而齿轮箱更换周期长,吊装成本高昂[1]。总之,花键联接的可靠性运行对齿轮箱乃至整个风机系统都至关重要。
目前,国内外学者对花键联接设计及强度校核方面的研究越发重视。余媛媛等人[3]对花键侧隙、修形量、夹角等参数进行了最佳组合的分析,寻求到了一种花键副齿面磨损量最小的设计参数组合,为后续花键参数设置做了铺垫。肖立等人[4]对轴线不对中和角向偏心对齿面微动损伤的影响做了研究,发现了花键齿面最危险的截面,准确预测了轴线不对中下花键磨损失效的寿命。梁全鹏等人[5]对超出DIN5480[6]标准的渐开线花键的设计做了研究,为齿数大于82、基准圆直径大于500的花键设计的合理性做了应用验证,为后续花键参数合理性设计做了铺垫和指引。沈瑞等人[7]研究了集中质量法计算不同花键径向间隙下的系统均载系数,为行星轮系均载设计提供了依据。喻天翔等人[8]考虑了加工精度及侧隙不确定性对花键疲劳寿命的影响,提高了对花键使用寿命预测的准确性。冉雄涛等人[9]对内花键轴和大齿轮过盈配合的变形量等做了分析,在此基础上,采用逆向螺旋角修形内花键,保证了内花键的轮齿侧隙。FREDERICK W等人[10]研究分析了花键齿面受载,提出了一种使花键受力更为均匀的方法。王庆国等人[11]利用解析法和有限元计算方法对花键传动的齿面接触应力进行了分析,发现了花键齿面接触区域并不是均匀受载的。胡娟娟等人[12]对花键齿面修形进行了研究,提高了花键齿面均载系数,为后续花键修形参数研究做了铺垫。WAVISH P M等人[13]开发了一种可以模拟多轴疲劳的试验装置,该装置可以模拟花键的微动接触疲劳失效行为,为研究花键疲劳失效和寿命预测提供了技术支撑。MEDINA S等人[14]利用边界元法分析了角度偏心对花键的齿面接触压力等影响,为后续花键齿面接触应力的分析做了铺垫。
以上是国内外学者从平齿根花键磨损及疲劳失效、侧隙对寿命的影响、花键参数设计等方面进行了研究。目前还没有学者对齿形花键参数设计和优化做深入研究。
为此,笔者将齿轮箱花键由常用的渐开线平齿根花键调整为渐开线齿形花键,并对齿形花键强度理论进行计算,优化齿廓参数,调整修形量,分析轮齿侧隙,验证渐开线齿形花键的扭矩传递能力。
1 渐开线平齿根花键
1.1 理论计算分析
风电齿轮箱优先使用压力角为30°平齿根的圆柱直齿渐开线花键,花键几何尺寸参照GB/T 3478.2[18]标准选取,一般使用齿面挤压强度计算渐开线平齿根花键联接强度是足够的[2],详细的计算可参考标GB/T M17855[14]《花键承载能力计算方法》。
花键齿面挤压强度计算可以使用专业的齿轮计算分析软件或使用工程算法。利用工程方法计算渐开线平齿根花键挤压强度计算公式如下:
(1)
式中:T为花键传递的扭矩,一般按齿轮箱额定输入扭矩及速比计算,N·mm;ψ为花键齿间不均载系数,根据DIN5480[5]规定的啮合质量确定,一般取0.7~0.8[9];z为花键齿数;L为工作齿面长度,mm;[p]为许用挤压强度,对于齿面经过热处理的σb≥600 MPa的材料,高强度球墨铸铁[p]=40 MPa~50 MPa,合金钢[p]=50 MPa~60 MPa[1];h为齿的工作高度。
h计算公式如下:
(2)
式中:Dm为平均直径。
Dm计算公式如下:
(3)
式中:dFa1.i为外花键齿顶成形直径;dFa2.i为内花键齿顶成形直径。
在专业的齿轮计算分析软件界面中,主要参数设置如图1所示。

图1 主要参数设置截面Fig.1 Main parameter setting cross section
图1中,笔者将花键的齿数、模数、压力角、变位系数、齿宽以及传递扭矩等参数设置完毕,点击计算完成后,可在计算报告中查看花键齿面挤压应力值。
根据计算结果判断是否满足设计要求,若齿面挤压应力值不满足要求,则需要重新调整齿数、齿宽及模数等参数,直至齿面挤压应力值满足设计要求。
1.2 应用现状
目前,根据风电齿轮箱风场应用情况及数据统计,一级行星传动中渐开线平齿根花键齿面挤压应力值在额定载荷下,建议控制在40 MPa之内,二级花键齿面挤压应力值控制在30 MPa之内。二级花键挤压应力值控制比一级花键严格的主要原因是二级行星传动的转速高,太阳轮浮动频率比高,花键易出现磨损失效。
齿轮箱型试验后,常见的平齿根花键联接的齿面啮合情况,如图2所示。

图2 平齿根内花键齿面Fig.2 Spline flank in flat tooth root
图2为齿轮箱型试验完后,二级行星传动中内花键轴平齿根花键齿面情况。该内花键齿面是经过氮化热处理之后的状况。
常用花键布置形式如图3所示。

图3 花键布置形式一Fig.3 Spline arrangement form I
根据式(1)可知:扭矩T增大,齿面挤压接触应力值p增大,但也可以通过增加花键齿数z和花键工作齿面长度L来降低齿面挤压接触应力值p;
由于齿轮箱轴向长度及花键宽径比限制,L增量有限。经常是调整花键齿数,z增加,花键分度圆直径d也增大(d=mz,m为花键模数,保持不变);
花键分度圆直径增加,会使轴承1和轴承2内外径尺寸及行星轮系的整体尺寸增大。
以上尺寸增大后,将导致齿轮箱的总重量及成本增加。总而言之,渐开线平齿根花键齿面挤压强度已经成为齿轮箱轻量化设计和降本的瓶颈。
2 渐开线齿形花键
2.1 理论计算分析
齿形花键的主要失效形式是磨损和微动磨损,轮齿断齿极少出现。减少磨损的主要措施是提高齿面硬度和改善润滑效果。
齿形花键的强度计算是依据GB/T 33923[17]标准从抗剪切、抗磨损和抗微动磨损及花键连接本体等强度的多方面进行分析和研究,具体计算和研究如下。
2.1.1 抗剪切强度校核
齿形花键的抗剪切能力是基于轮齿工作高度一半处来核算的。强度计算时,通常按该处的剪切面积、直径及轮齿有效啮合齿宽和轮齿芯部材料的许用剪切应力来校核花键。
若花键外齿考虑使用系数KA后的剪切强度,公式如下:
(4)
式中:SS为花键外齿使用系数KA后的剪切应力,N/mm2;KA为工况系数,常取1;b′为花键齿的有效啮合齿宽,mm;极限值为b′/d≤0.33。
Km为载荷分布系数,其计算公式如下:
Km=1+f∑/0.004
(5)
式中:f∑为太阳轮的角度偏差,rad。
太阳轮角度偏差很小,一般可通过控制精度、增加太阳轮的长度、或装配调整等措施,把太阳轮有可能产生的角度偏差控制在合理的极限值之内,极限偏差值为0.001 rad。
d为工作高度一半处的直径,mm。其计算公式如下:
d=(dosp++disp)/2
(6)
式中:dosp为外花键大径,mm;disp为内花键小径,mm。
SSA为芯部材料的许用剪切应力,单位N/mm2。其计算公式如下:
SSA=34.5+6.9*HC
(7)
式中:HC为芯部硬度,例如QT700-2A,可以取值30 HRC。
2.1.2 抗磨损校核
花键内外齿齿面磨损的主要原因是在高载荷、润滑油中有污染物和磨料颗粒,以及在润滑不足的情况下发生相对运动造成的。磨损校核计算公式是依据假设所有的轮齿全部承担载荷,考虑使用系数KA后齿面的挤压应力值。其计算公式如下:
(8)
式中:SC为考虑使用系数KA后的齿面挤压应力,N/mm2;z为花键齿数;SCA为许用挤压应力值,N/mm2。
SCA计算公式如下:
(9)
式中:Hs为内外花键齿面硬度较低的一个齿面硬度,HRC;例如QT700-2A,可以取值55 HRC;KSCA为材料的许用应力值,正火或调质时,KSCA=0.065;齿部表面硬化时,KSCA=0.057。
2.1.3 花键连接本体强度校核
1)外花键轴扭转失效校核
外花键轴最大扭转剪切应力的计算公式如下:
(10)
式中:SSS为轴的最大剪切应力,N/mm2;dmin为轴的最小外径,mm;din为空心轴的内径,mm。
2)内花键筒壁爆裂校核
内花键轴筒壁爆裂的计算公式如下:
st=Km(s1+s2)+s3≤stA
(11)
式中:st为总的拉应力,N/mm2。
stA为许用应力,单位N/mm2。其计算公式如下:
stA=6.9×(9+HC)
(12)
s1为啮合径向力产生的引起筒壁爆裂的应力,单位N/mm2。其计算公式如下:
(13)
式中:an为花键压力角,(°),可以选用20°压力角;tw为内花键的筒壁厚度。
s2为花键齿弯曲拉应力,单位N/mm2。其计算公式如下:
(14)
式中:Ys为齿形系数(30°花键齿采用1.5)。
s3为离心力产生的圆周应力,单位N/mm2。计算公式如下:
(15)
式中:n为花键的转速,r/min;dso为内花键筒壁的外径,mm;dri为内花键的齿根圆直径,mm。
通过以上计算分析,笔者校核了渐开线齿形花键联接的强度及传扭能力,为接下来的齿轮箱轻量化和降本设计做好了铺垫。
2.2 参数优化设计
2.2.1 齿形系数
笔者拟通过研究花键齿形系数来提高花键齿面接触及齿根弯曲强度。
花键模数根据GB/T 3478.2[18]标准选取,风电齿轮箱花键常用模数为8~12,主要根据生产厂家现有刀具选取。
平齿根花键变位系x*=0,而内外齿形花键常采用正变位系数,常用x*=0.5。选取正变位系数,可增加轮齿齿厚,减小花键齿的尺寸,提升花键承载能力[3]。
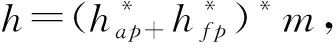
花键齿廓参数设置如图4所示。
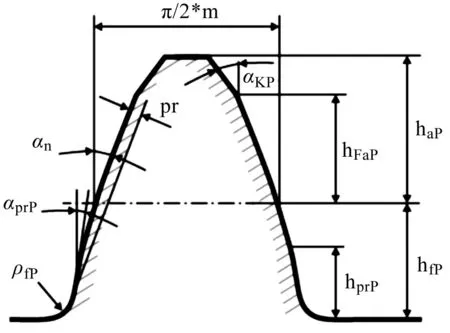
图4 花键齿廓参数Fig.4 Spline tooth profile parameters
在专业的齿轮计算分析界面中,齿形花键齿廓主要参数的设置如图5所示。

图5 花键齿廓主要参数设置界面Fig.5 The main parameter setting screen of spline tooth profile
当压力角为30°时,渐开线平齿根花键齿廓曲线如图6所示。
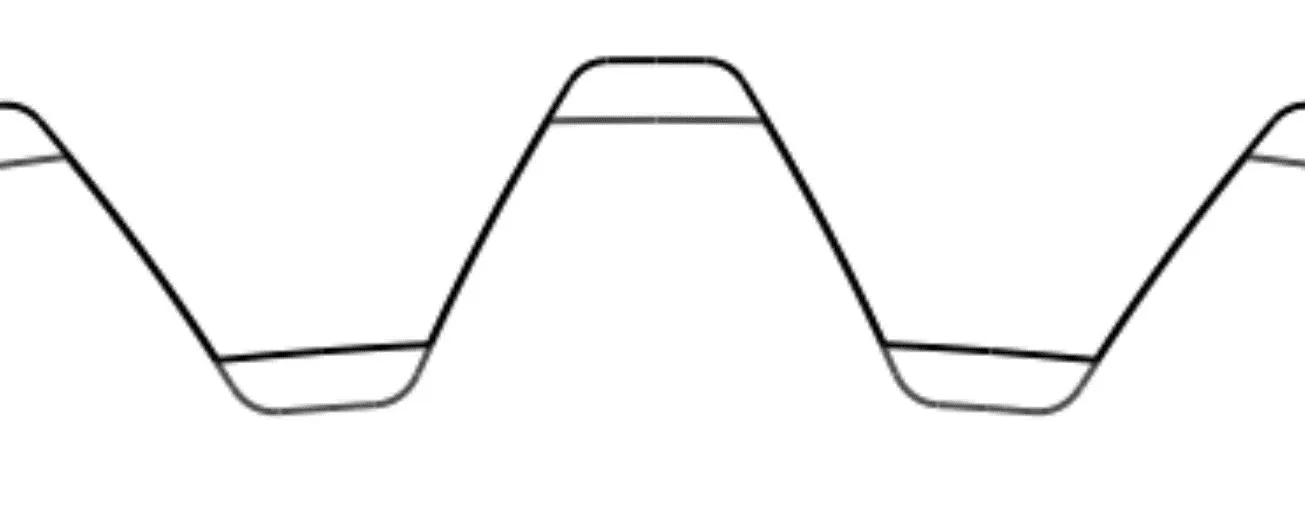
图6 渐开线平齿根花键啮合齿廓Fig.6 Involute flat tooth root spline meshing tooth profile
压力角20°时,经过调整齿形系数后的齿形花键齿廓曲线如图7所示。
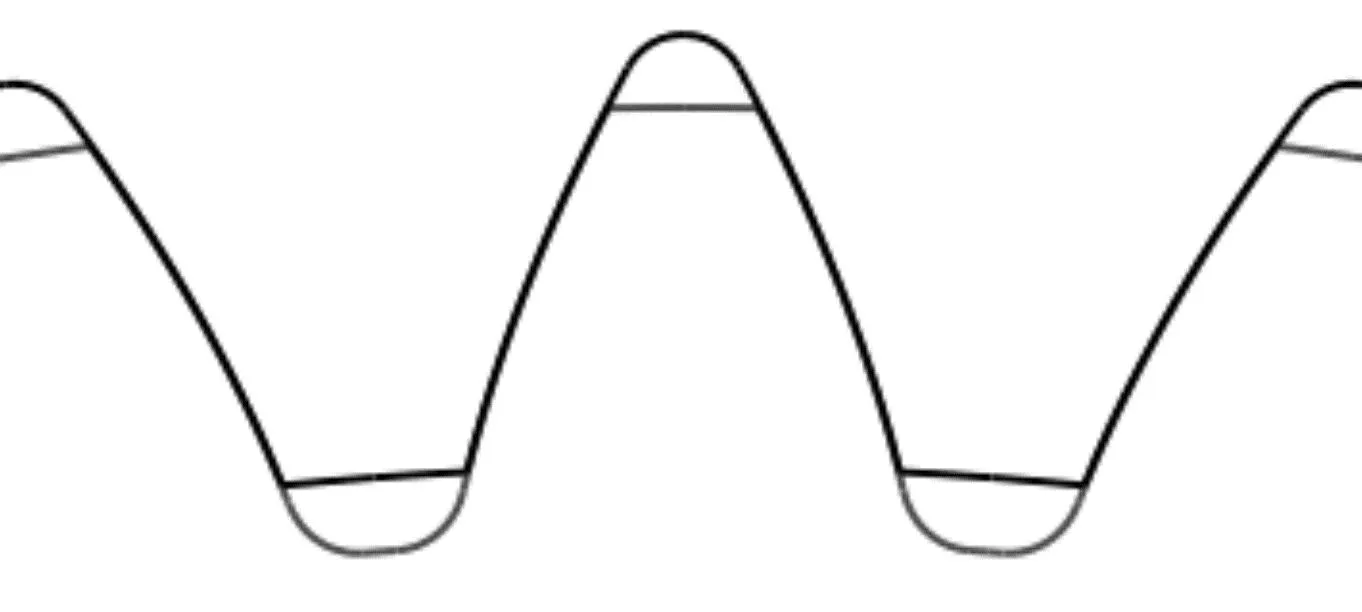
图7 渐开线齿形花键啮合齿廓Fig.7 Involute toothed spline meshing tooth profile
从图6和图7中的齿廓曲线可明显分析出:齿形花键渐开线啮合长度较长,主要是渐开线变位系数的影响。
在扭矩和分度圆直径相同的情况下,笔者利用专业的齿轮计算分析软件计算花键齿面挤压应力值,平齿根花键挤压应力值约为齿形花键挤压应力值的2.2倍,变位系数对挤压应力值的影响占主要因素。
根据ISO6336标准及以上应力分析可知:改善齿轮啮合的渐开线长度,可提高齿面接触强度,延缓齿面磨损,延长齿轮的使用寿命。
2.2.2 轮齿侧隙
由于太阳轮通常作浮动件来完成行星轮均载工作,可以利用花键或齿轮的啮合来支撑浮动件,但应有足够大的径向间隙,以免出现零侧隙或摩擦限制太阳轮浮动的现象[2]。
行星级中太阳轮工作时,其偏转角(浮动量)很小,通常情况下渐开线花键的侧隙应与齿轮侧隙大致相当,以保证相同的浮动量[1]。太阳轮距花键的距离越大,浮动效果越好,所以内花键位置尽可能远离行星轮系。若中间轴上内花键设计位置正对输出大齿轮烘装配合处,则需考虑烘装后轴径缩小,致使内花键轮齿侧隙变小的情形。
为满足齿轮箱轻量化设计需求,也有学者在太阳轮内孔处设计内花键,在二级行星架输入轴处设计外花键。该结构设计花键侧隙时,除了考虑齿轮的侧隙外,还需考虑制造偏差和行星轮轴承游隙(当齿轮传动装置刚度较大时,变形量很小,可忽略)。
制造偏差主要是指太阳轮和行星轮的径向综合总偏差,以及太阳轮和行星轮中心距的极限偏差;行星轮轴承游隙主要是指各行星轴承最大径向工作游隙的1/2。更为详细的介绍请参考标准GB/T33923[17]。
二级行星架输入轴处设计外花键布局形式如图8所示。
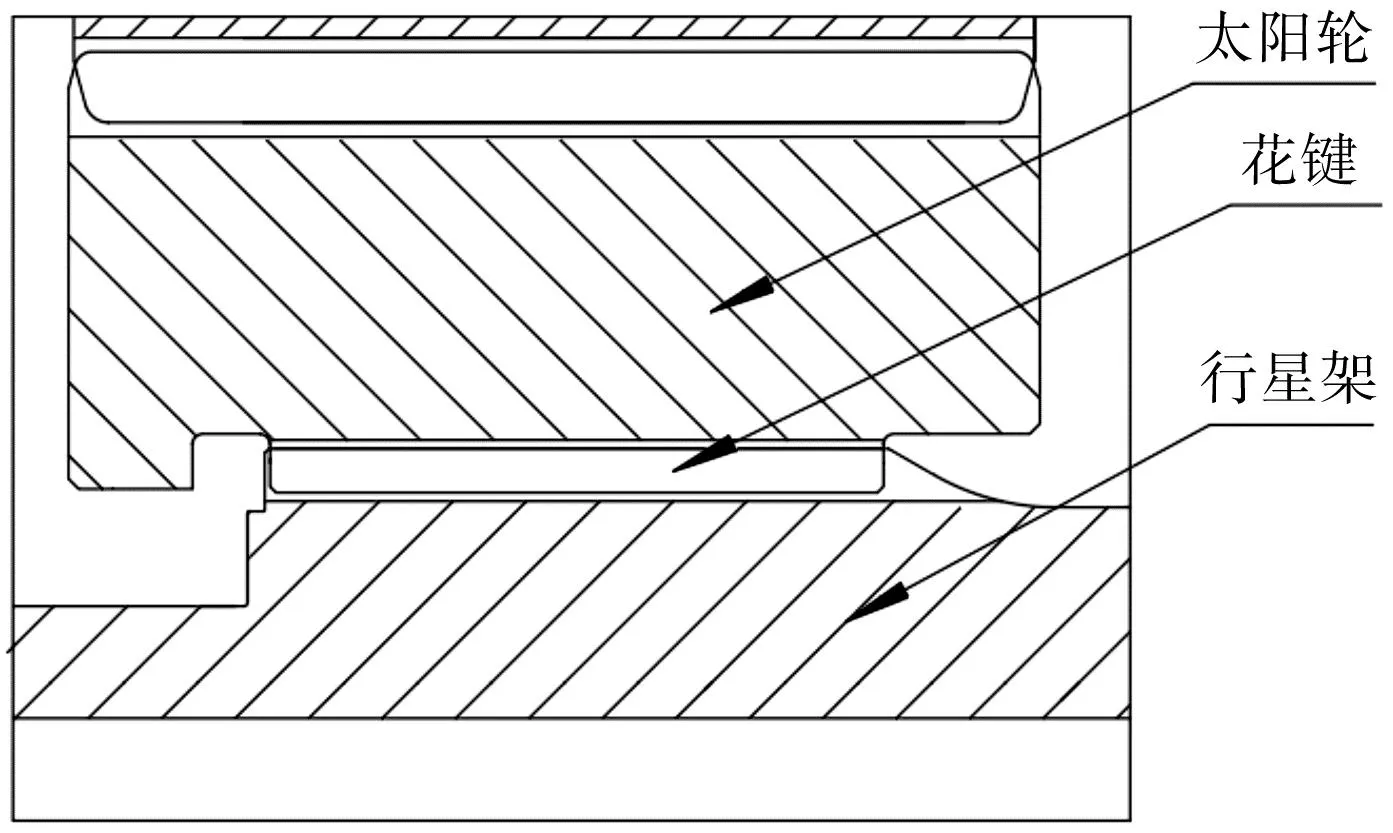
图8 花键布置形式二Fig.8 Spline arrangement form II
笔者调整了渐开线齿形花键的齿厚公差,保证了花键的侧隙,满足了太阳轮浮动量,补偿了齿轮啮合的对中偏差,降低了行星轮系不均载系数,提高了行星轮系中齿轮的承载能力。
2.2.3 齿面修形
对于花键齿面修形等问题,国内外学者做了很多研究和分析。为了提高花键齿承载能力,改善齿端部应力集中,延长花键齿寿命,学者们常对花键进行齿向修鼓,有必要时可增加齿向螺旋角修形。
风电齿轮箱常用花键鼓形修形如图9所示。
如需适当地对花键进行修鼓,修形量建议控制在0.03 mm~0.06 mm范围内,公差取值±0.005 mm。
花键螺旋角修形,常根据花键轴花键齿宽方向的扭转变形量决定。扭转变形量常根据专业的齿轮计算分析软件或其他软件的分析决定。
3 试验及结果分析
渐开线齿形花键的强度满足以上设计要求后,笔者通过齿轮箱型式试验,验证渐开线齿形花键实际传扭的能力和齿面接触状况。
齿轮箱型式试验台位布置示意图如图10所示。
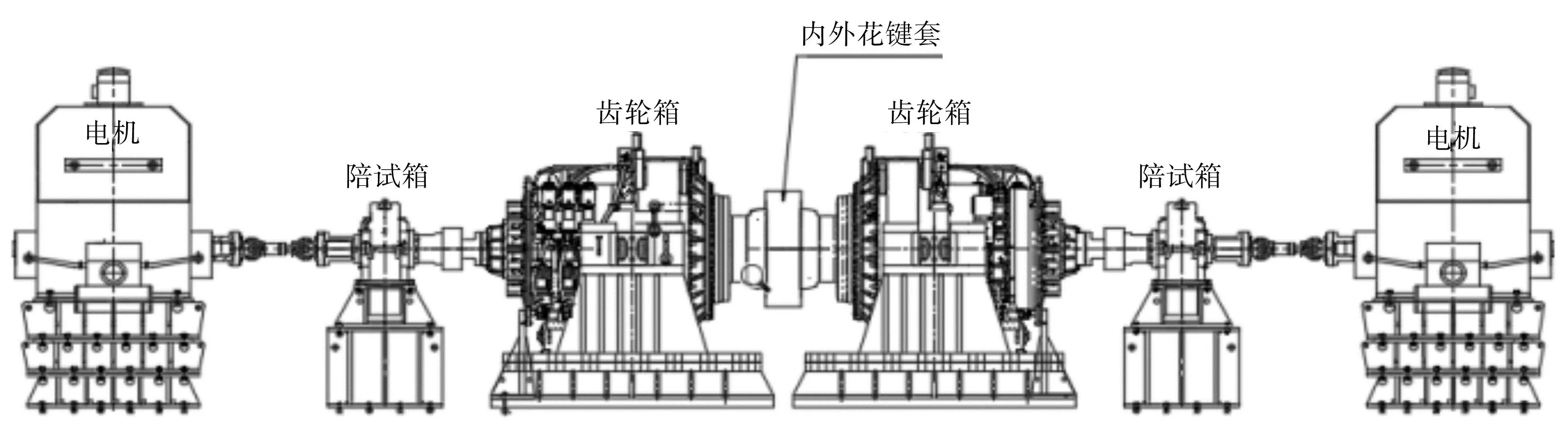
图10 齿轮箱型式试验台位布置示意图Fig.10 Schematic diagram of the layout of the gearbox type test bench
该试验为齿轮箱母子机器面对面联结对拖试验。电机与陪试箱通过万向联轴器联接;陪试箱与齿轮箱高速轴之间通过内外花键或万向联轴器联接;齿轮箱与齿轮箱低速端通过内外花键联接。左端电机联通陪试箱后,笔者将转速及扭矩调整为满足齿轮箱需求的参数。
该试验中,齿轮箱的额定输入转速为8 r/min,额定输入扭矩为5 500 kN·m,总试验时间大于50 h(等效疲劳寿命1年)。
齿轮箱型式试验步骤,即齿轮箱的加载载荷、时间及转速,如表1所示。
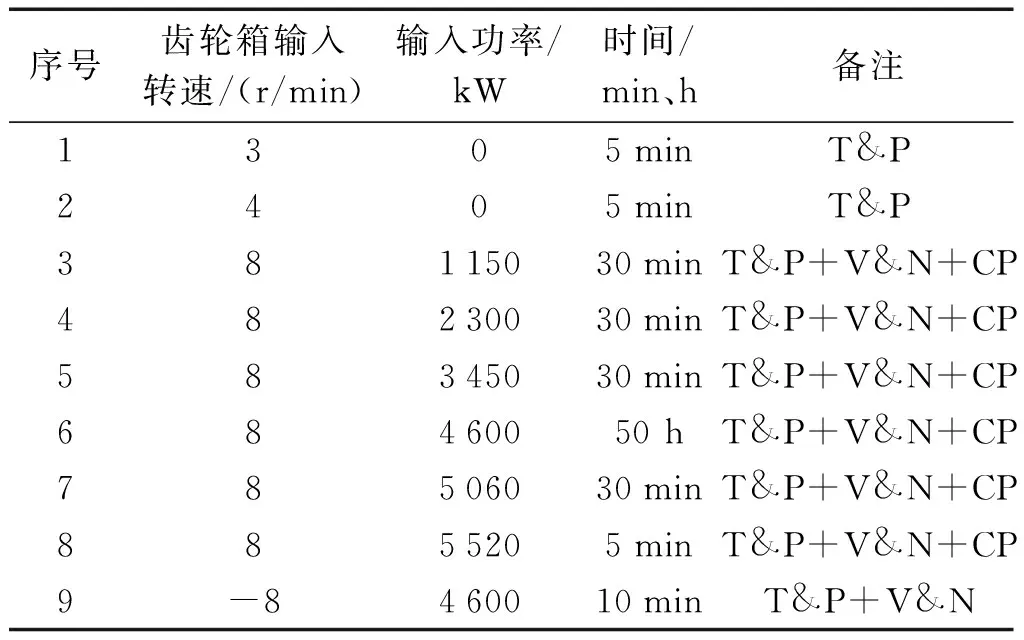
表1 齿轮箱型式试验步骤Table 1 Gearbox type test steps
齿轮箱式试验过程中,笔者需要实时监测其运行状态,需每隔15 min记录齿轮箱的振动速度、加速度、噪音、传递效率及行星轮系齿间均载系数、油温、油压等试验数据。
根据VDI3834[20]标准可知,齿轮箱的振动速度不超过3.5 mm/s,加速度不超过7.5 m/s2。
在各载荷下,笔者按测振点测量齿轮箱的振动值。
齿轮箱的振动速度数值记录曲线如图11所示。
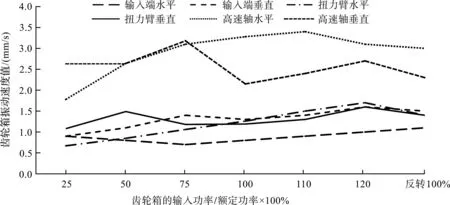
图11 齿轮箱振动测试速度曲线图Fig.11 Gearbox vibration test speed curve
从图11中分析可知:齿轮箱各个测振点的速度值都小于3.5 mm/s,满足VDI3834标准要求。
由于高速轴转速较高以及后箱体刚性不足等原因,高速轴测量的速度值比其他测振点数值都高,但都满足设计要求。
在各载荷下,笔者按测振点测量齿轮箱的振动加速度值。
齿轮箱的振动测试加速度数据曲线如图12所示。

图12 齿轮箱振动测试加速度曲线图Fig.12 Gearbox vibration test acceleration curve
分析图12加速度记录曲线图可知:齿轮箱的测量加速值满足VDI3834标准要求;测试的振动加速度值与速度值高点一致,都出现在高速轴位置。
在各载荷下,噪声检测点在齿轮箱输出端,并距离齿轮箱1 m远处。按ISO 8579-1[21]标准要求,齿轮箱振动噪音不超110 dB。
在齿轮箱型式试验过程中,振动噪音测试数据如图13所示。
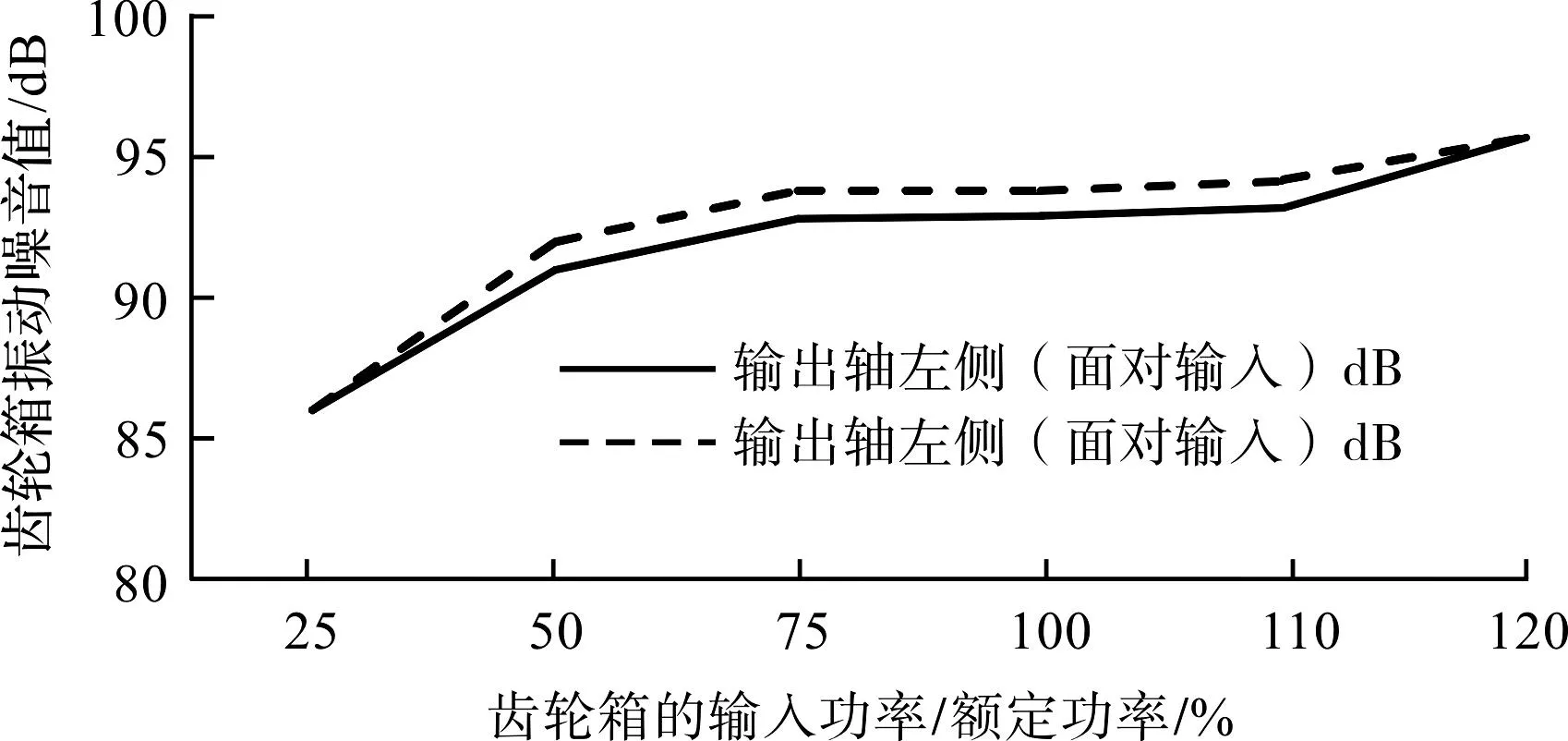
图13 齿轮箱型式试验噪音数据曲线图Fig.13 Noise data plot of gearbox type testtest
从图13曲线值可知:齿轮箱噪音最大值为98 dB,满足齿轮箱设计规范要求。齿轮箱运行噪音值一般没有强制性要求,但要特别注意齿轮箱运行过程中的异响情况,可能是某些零部件失效的预警。
齿轮箱机械效率(传递效率)如图14所示。
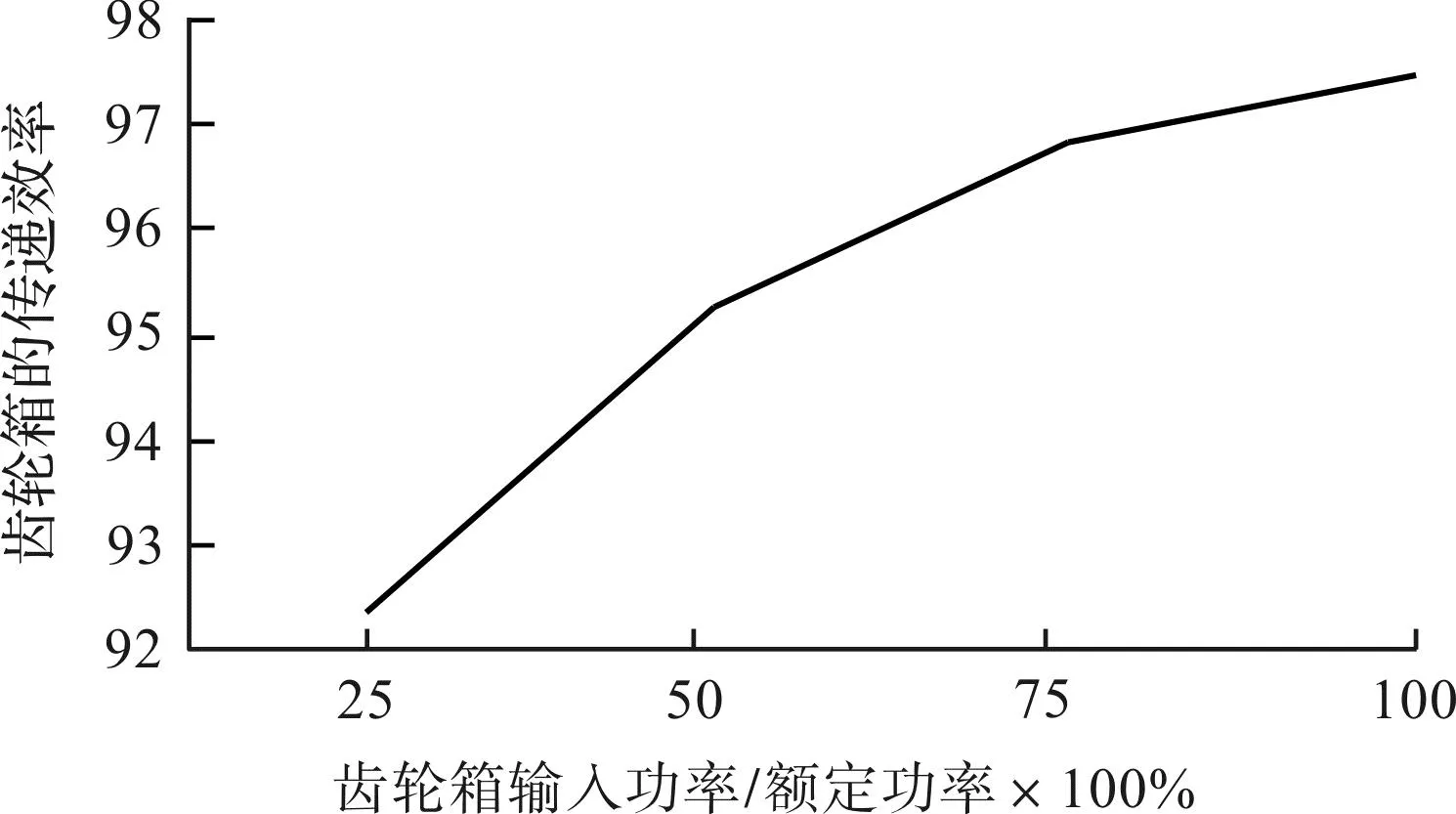
图14 齿轮箱传递效率数据曲线图Fig.14 Gearbox transmission efficiency data curve
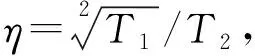
该型式试验的齿轮箱为三级行星传动结构,100%额定载荷下,齿轮箱的传递效率在97.5%左右。测试试验值与设计值相符合,满足要求。
在齿轮箱型式试验过程中,行星轮系的均载系数测量值如图15所示。
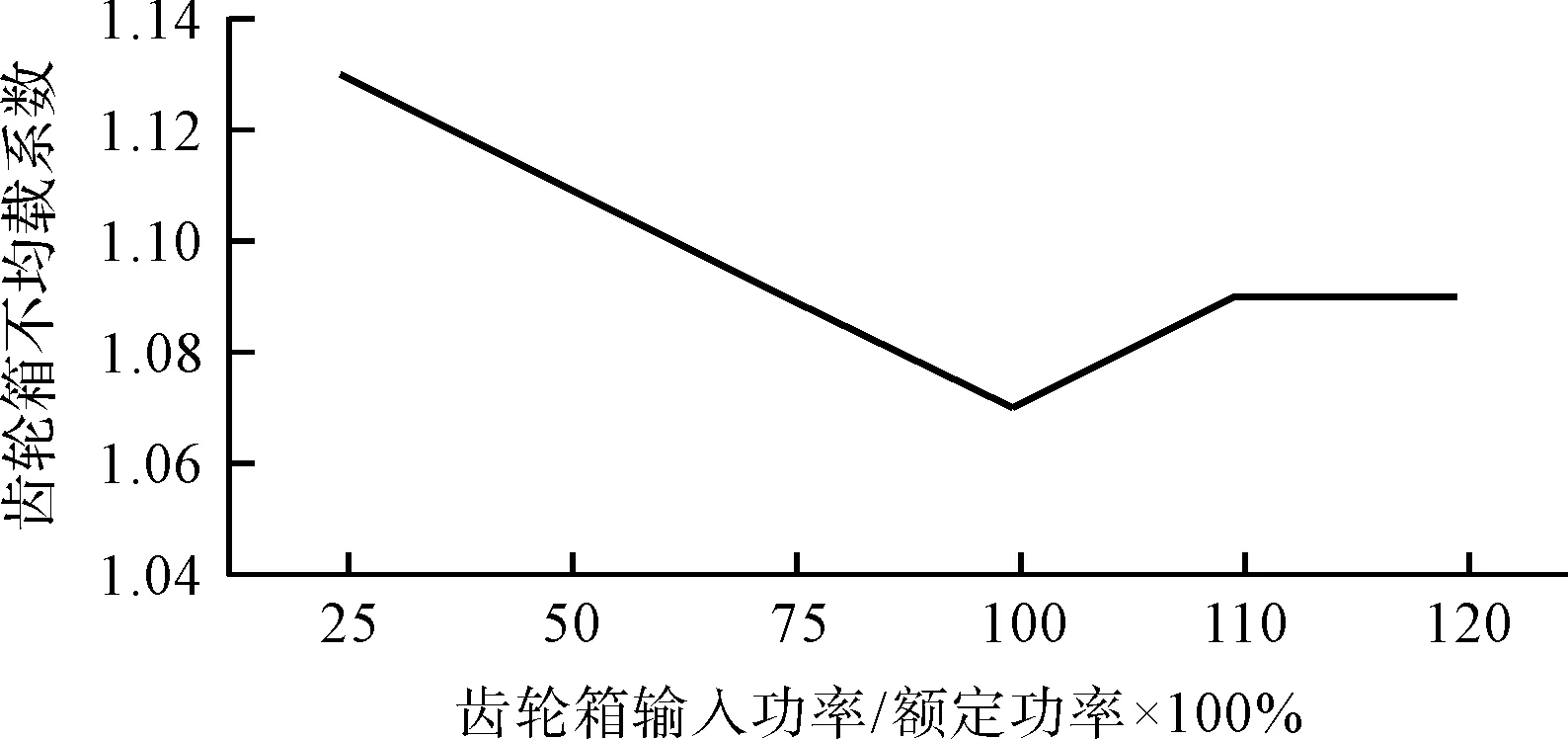
图15 齿轮箱行星轮系齿间均载系数曲线图Fig.15 Curve of the inter-tooth load coefficient of the gearbox planetary gear train
该齿轮箱型式试验测量不均载系数的行星轮个数为5。设计齿轮箱强度时,不均载系数Kγ取值为1.1。
从图15可知:100%额定载荷下,Kγ为1.07,通过计算得到其各个工况下Kγ均值小于1.1。可见太阳轮的浮动目前可以很好地满足5个行星轮均载。
齿轮箱试验完毕之后,内花键齿面情况如图16所示。

图16 内花键齿面Fig.16 Inner spline tooth flank
齿轮箱试验完毕之后,外花键齿面情况如图17所示。

图17 外花键齿面Fig.17 Outer spline tooth flank
齿轮箱试验完毕后,笔者对齿轮箱进行拆检,查看齿面、轴承等应用情况。
通过图16及图17可以看出:内外齿形花键齿面无断齿、疲劳点蚀、异常磨损、裂纹等齿面异常啮合现象;齿面通过修鼓和修螺旋,花键轮齿啮合的接触斑从着色上面看,100%额定载荷下,齿高≥70%,齿长≥90%;观察齿面磨损情况,发现无齿端磨光高点,齿面受力较均匀。
通过以上分析可知,该研究中设计的花键可以很好地实现传扭功能,同时还可以满足齿轮箱轻量化设计需求。
4 结束语
平齿根花键设计已经成为风电齿轮箱轻量化设计的技术瓶颈。针对风电机组齿轮箱渐开线平齿根花键磨损失效,及齿轮箱轻量化设计对花键结构的需求,笔者对渐开线齿形花键的设计进行了深入研究,即对渐开线齿形花键的强度理论分析、齿形参数优化、轮齿侧隙设计、齿面修形等方面进行了研究;通过齿轮箱型式试验,查看了花键齿面实际应用情况,验证了齿形花键的传扭能力。
具体结论如下:
1)在扭矩和分度圆直径相同的情况下,平齿根花键挤压应力值约为齿形花键挤压应力值的2.2倍,可见齿形花键的传扭能力提高了约10%;
2)齿形花键强度可以根据GB/T33923标准,利用工程算法,从花键的抗剪切、抗磨损以及花键本体等几个方面来校核设计;
3)优化了齿形花键的变位系数、齿顶高系数及齿根高系数,增加渐开线花键轮齿厚度及渐开线长度可以增强花键接触及弯曲强度;
4)设计花键侧隙时,可以通过调整渐开线齿形花键的齿厚公差,保证花键的侧隙,满足太阳轮浮动量,以补偿齿轮啮合的对中偏差,降低不均载系数,提高轮齿承载能力;
5)对花键进行了齿向修鼓,有必要时可增加齿向螺旋角修形,以避免花键齿端部应力集中的现象,改善齿面受力情况。
在目前的研究中,花键齿面啮合情况只是齿轮箱在厂内的试验结果。在后续的研究中,笔者会根据齿轮箱风场实际运行情况,进一步优化调整齿形花键的修形参数,以满足设计的需求。

