基于mRMR-SOM的异步电机轴承故障诊断研究*

刘 文,周智勇,蔡 巍

(海军潜艇学院 动力操纵系,山东 青岛 266000)

0 引 言

异步电机是一种的重要电气设备,其用途非常广泛。因此,确保其安全稳定运行具有重要的意义。异步电机的潜在故障隐患会造成设备损伤。而轴承故障是异步电机故障类型中最常见的种类,其占比可以达到50%左右。因此,对轴承故障进行诊断尤为重要。

目前,轴承故障诊断的经典方法是提取振动信号故障特征进行分析判断。

陈宗祥等人[1]将小波包分解、方差贡献率检验与经验模态分解方法相融合,利用双谱分析的方法提取了调制在高频信号中的故障特征频率,达到电机轴承故障诊断的目的;但该方法的准确性易受到电机固有特性的影响。宿文才等人[2]将极点对称模态分解算法、信息熵与相关性筛选方法和Hilbert变换相结合,提取了轴承关键特征并进行了故障诊断;但轴承故障特征分量易淹没于基波和噪声,易造成误诊和误判。针对此类问题,HOANG D T等人[3]提出了将深度学习和信息融合方法相结合,采用了决策级信息融合技术对所有卷积神经网络的信息进行融合,达到了对轴承故障进行精确诊断的目的;但卷积神经网络结构复杂,且需要大量训练样本才能达到较好的诊断精度。

此外,电机电流信号分析法(motor current signal analysis,MCSA)也被应用于轴承故障诊断。

杨江天等人[4]对定子电流进行了小波包分解,通过对比各节点系数的均方根值和峭度指标变化情况,判断电机是否存在轴承故障;但该方法与振动信号分析方法类似,MCSA同样易受到环境因素和电机固有特性等问题的干扰。为了解决这一问题,SAUCEDO-DORANTES J J等人[5]提出了将振动信号、电流信号和温度信号相融合的方法,提取故障特征用于轴承故障诊断,能够避免部分特征淹没于噪声的问题;但高特征维度会导致计算冗余或掺入无用特征,特征降维技术成为故障诊断方法十分重要的环节。

常用的特征降维方法有主成分分析法[6](principal component analysis,PCA)和核主元分析法[7](kernel principal component analysis,KPCA)等。但PCA方法可能存在筛除核心元素的问题,造成诊断准确率下降;而KPCA对非线性关系特征不敏感,需要人为调整核函数以取得较好的降维效果。

最大相关最小冗余特征选择(mRMR)算法[8]是以互信息为计量准则的特征降维方法,能够筛选出与标签相关度最高,且特征间冗余度最低的特征,从而达到强化区分能力和提升精度的效果。

自组织映射神经网络(SOM)[9]能够将高维空间中相似的样本点映射到网络输出层中的邻近神经元,训练速度快,具有良好的自组织性和鲁棒性[10]。

基于此,笔者采用一种基于mRMR-SOM的异步电机轴承故障诊断方法,并在实验室环境搭建异步电机故障诊断试验平台。

首先,笔者采集不同状态下的电机振动、电流和电压信号,对信号进行时域和频域分析,提取统计特征量;然后,利用mRMR对特征重要性进行评估,以互信息为评价准则,在保证分类器准确率的前提下筛选强区分能力特征;最后,使用SOM对测试样本进行分类,验证该诊断方法的有效性和正确性。

1 基于互信息的特征降维

笔者采用以互信息为基本背景的mRMR算法,对特征集进行降维处理。

1.1 互信息的基本概念

互信息的概念脱胎于信息论,是变量间相互依赖程度的度量依据,表示两个变量相同部分所占的比例[11]。

下面笔者对基于互信息的特征降维算法中涉及的基本概念分别进行介绍。

1)信息熵[12]。信息熵是使用统计学的方法,用于体现随机变量所蕴含信息量大小的工具。

设随机变量X={x1,x2,…,xn},其信息熵的表达式为:

(1)

式中:p(xi)为xi发生的概率。

p(xi)在极限情况下,当随机变量X中的变量均为x时,p(xi)=1。此时信息熵H(X)=0,表明该样本集包含的信息量为零,因为随机变量X中仅含有变量x。

信息熵的引入能够帮助人们更好地理解数据的不确定性,一般来说一件事情发生的可能性越高则代表信息熵越低,说明该事件包含的信息量越少。

2)联合熵。与信息熵类似,联合熵是信息熵的一种推广。当有两个随机变量时,使用信息熵的公式就可以得到联合熵,它表示两个随机变量包含的信息总和。

假设有两个随机变量X和Y,其分布满足联合概率分布函数P(X,Y),则其联合熵的表达式为:

(2)

3)条件熵。条件熵H(X|Y)表示在给定Y变量的条件下X变量的不确定程度,定义如下:

(3)

4)互信息[13]。互信息可以用来衡量两变量间的相关程度,假设有两个随机变量X={x1,x2,…,xn}和Y={y1,y2,…,yn},它们满足联合概率分布P(X,Y),则变量X和变量Y之间的互信息I(X;Y)表示为:

(4)

由互信息定义可知,当两变量间的相关性越大,其互信息值也就越大;反之,当两个变量之间完全无关时,互信息的值应当为0。因此,借由互信息值的大小即可判断变量间相互依赖的程度。

此外,互信息还可以用熵进行表示,公式如下:

I(X;Y)=H(Y)-H(Y|X)

(5)

当互信息由熵值表达时可以看出,变量X和变量Y之间的互信息值的大小可以理解为变量Y在变量X已给定的情况下其未知程度的减少量。如果在X能够完全确定Y,则H(Y|X)=0,此时两变量的互信息I(X;Y)=H(Y),若X与Y互不相关,则H(Y|X)=H(Y),此时I(X;Y)的值为0。

可见,互信息可以理解为用于度量变量间独立程度的衡量标准。

5)相关性。假设Xm为待选特征集合,C为类标签集合。相关性用于表征特征集中的特征与标签集中的标签的关联程度,采用互信息I(Xm;C)直观体现。I(Xm;C)越大,则特征向量与类标签关联度越高。

6)冗余性[14]。假设S为已选择的特征集合,则冗余性表示待选的特征向量与S的相关性,同样以互信息为衡量标准[15]。若xm与S的互信息值越大,则表明待选特征xm与已选择的特征集合S的冗余度越高。该方法可以用于对冗余特征的筛除。

1.2 算法流程

mRMR算法计算特征与类标签的互信息和特征与特征间的互信息,以达到对特征进行筛选降维的目的。其算法流程如下[16]:

步骤1。初始化特征集合。假设S为已选特征集,Xm为待选特征集,C为标签集;

步骤2。对Xm中的特征,执行下列步骤:

1)计算最大相关度。遍历Xm,寻找与C间的最大相关性,其评价准则为:

maxD(Xm,C),D=I({xi,i=1,…,m};c)

(6)

2)计算最小冗余度。遍历S,寻找特征间的最小冗余度,其评价准则为:

(7)

3)获取最大相关最小冗余特征:

maxΦ(D,R),Φ=D-R

(8)

4)将所得特征放入S中,并从Xm中删除该特征。

步骤3。判断S中的特征数量是否已满足规定的终止条件,若满足条件,则输出S;否则,重复步骤2。

1.3 基于mRMR的特征选择

特征选择的目的是在不降低原有特征集包含信息量的基础上,选择出能够表征电机运行状态的特征,降低原有特征集维度,提高运算效率。

笔者使用mRMR算法进行特征选择,其具体步骤如下:

1)采用增量选择的方法从原始特征集中选择n个连续特征,得到n个连续特征集,S1⊂S2⊂…⊂Sn;

2)对比所有n个连续特征集S1,S2,…,Sk,…,Sn(1≤k≤n),并将所有待选特征集送入分类器中进行对比,选择出能够获得高分类准确率的Sk,并将其纳入一个备选集合Ω;

3)在Ω中,选择分类准确率最高的那部分Sk,其中k值最小的待选集合即为特征选择后的最优特征集。

2 基于SOM故障诊断方法

2.1 SOM的概念及结构

SOM是由芬兰学者KOHONEN T模拟人脑神经元自主学习的能力,开发出的一种无监督、自学习的神经网络。它能够在庞大的样本空间中找到相似的部分并映射到低维空间中,形成聚类并记住这种逻辑关系,训练后的网络能够对输入样本进行自动分类。

SOM具有将高维数据映射至低维空间,并保持原有数据拓扑结构不变的特点,网络由输入层和输出层组成。与其他神经网络不同,SOM不包含隐含层,其结构更为简单,算法复杂程度低且有效。输入层与输出层间直接使用权值向量进行连接,输出层中的每个神经元均与所有输入向量连接,以保证输入向量能够在输出层上进行良好的映射。

SOM网络结构如图1所示。

图1 SOM网络结构示意图Fig.1 The structure of SOM

图1中,下层为输入层,上层为输出层,通过权值连接后,相同类型的输入向量能够在输出层中进行自动聚类。图1输出层中不同颜色的神经元即代表不同的数据类别。

2.2 SOM神经网络算法步骤

SOM神经网络属于竞争型学习神经网络。训练开始后,输入向量会计算与之连接的所有输出层神经元之间的欧式距离,以距离的远近作为神经元获胜的依据,输出层中与该输入向量距离最小的神经元,即为获胜神经元,其有权利会同邻域范围内的所有神经元进行权值的更新,使其与输入向量间的距离进一步减小;不同的输入向量可能在输出层中对应不同的获胜神经元,因此,输出层中不同位置的神经元均有可能被激活。

其算法步骤如下[17-18]:

步骤1。设置输出层神经元个数、初始权值向量、学习率、邻域尺寸等参数以使网络初始化;

步骤2。设数据样本集X中的输入向量x(t)为N维,t为迭代次数,每次迭代从X中随机抽取x(t);

步骤3。计算输出层中每一个神经元的权值和输入向量的欧式距离,并找到输入向量x(t)所对应的获胜神经元:

c=argmini{‖x(t)-mi(t)‖}

(9)

式中:c为获胜神经元;mi(t)为权值向量;

步骤4。同步更新获胜神经元c及其邻域范围内的其他节点的权值:

mi(t+1)=mi(t)+hci(t)[x(t)-mi(t)]

(10)

式中:hci(t)为邻域函数,邻域内不同的节点根据距离的远近,其权值更新的幅度不同;

步骤5。更新网络参数:

hci(t)=α(t)exp(-sqdist(c,i)/2σ2(t))

(11)

式中:α(t)为学习率函数;σ(t)为邻域尺寸函数,二者均是时间t(也即迭代的次数)的单调递减函数,α(t)的取值范围一般在(0,1)之间;sqdist(c,i)为获胜神经元c与邻域内节点i之间几何距离的平方。

随着迭代的不断进行,邻域函数也会不断地更新,以使网络逐渐趋于收敛;

步骤6。检查结果是否满足既定要求,不满足则继续迭代;满足要求则循环结束,训练完成。

2.3 U-Matrix可视化

U矩阵[19](unified distance matrix,U-Matrix)可对SOM的分类结果进行展示,它以距离作为度量标准,以二维网络结构显示结果。U-Matrix中的每个网格点表示该神经元与周围神经元之间的距离。

由聚类的性质可知,聚类是利用数据的相似性对混乱的原始数据集进行聚合和分离,从而划分出一定的类别。U-Matrix即是利用距离度量的方法使SOM分类结果可视化。U-Matrix可储存SOM中每一个神经元与其邻近神经元间的距离,数值的大小表示距离的远近。

为了更形象地表征这种距离度量方式,笔者在U-Matrix中引入RGB颜色,并对不同的颜色赋予不同数据值:深色表示距离远、数值大,浅色则代表距离近、数值小,根据颜色的深浅即可判断距离的大小。相似性高(即距离小)的数据即属于同一类数据,相似性小(即距离大)的数据即属于不同类数据。

U-Matrix实际上只起到了存储SOM中神经元相对距离的作用,并没有改变神经元位置。因此,采用这种方法不但使SOM可视化,还保留了原始数据的拓扑结构。

3 试验验证

3.1 试验平台及试验设计

笔者设计了一个异步电机轴承故障诊断试验台。该试验台主要包括异步电机、直流发电机、电阻负载箱、传感器、数据采集仪和上位机等。

试验台总体布置图如图2所示。

图2 故障诊断试验平台Fig.2 Fault diagnosis test platform

该次试验中,笔者所用异步电机型号为Y132M-4,轴承型号为6308A。

为了模拟轴承外圈故障,笔者使用线切割机在轴承外圈处开贯穿型凹槽,其中,开槽宽度为2.0 mm,深度为1.5 mm,如图3所示。

图3 开贯穿型凹槽的故障轴承Fig.3 Faulty bearing

故障轴承安装于异步电机输出端。

试验过程中,笔者设置健康和轴承故障两种运行状态,分别采集振动、电流和电压信号。每种状态分别采集100组数据,共计200组试验样本。

笔者按照1 ∶1的比例对训练样本与测试样本进行分割,如表1所示。

表1 数据分组情况Table 1 Data grouping

3.2 信号分析及特征选择

判断电机是否发生轴承故障需要选择合适的特征,当出现轴承故障时,原有的稳定运行状态被破坏,其振动特性和电流特性均会发生改变。

在不同运行状态下,振动信号的时域波形对比图如图4所示。

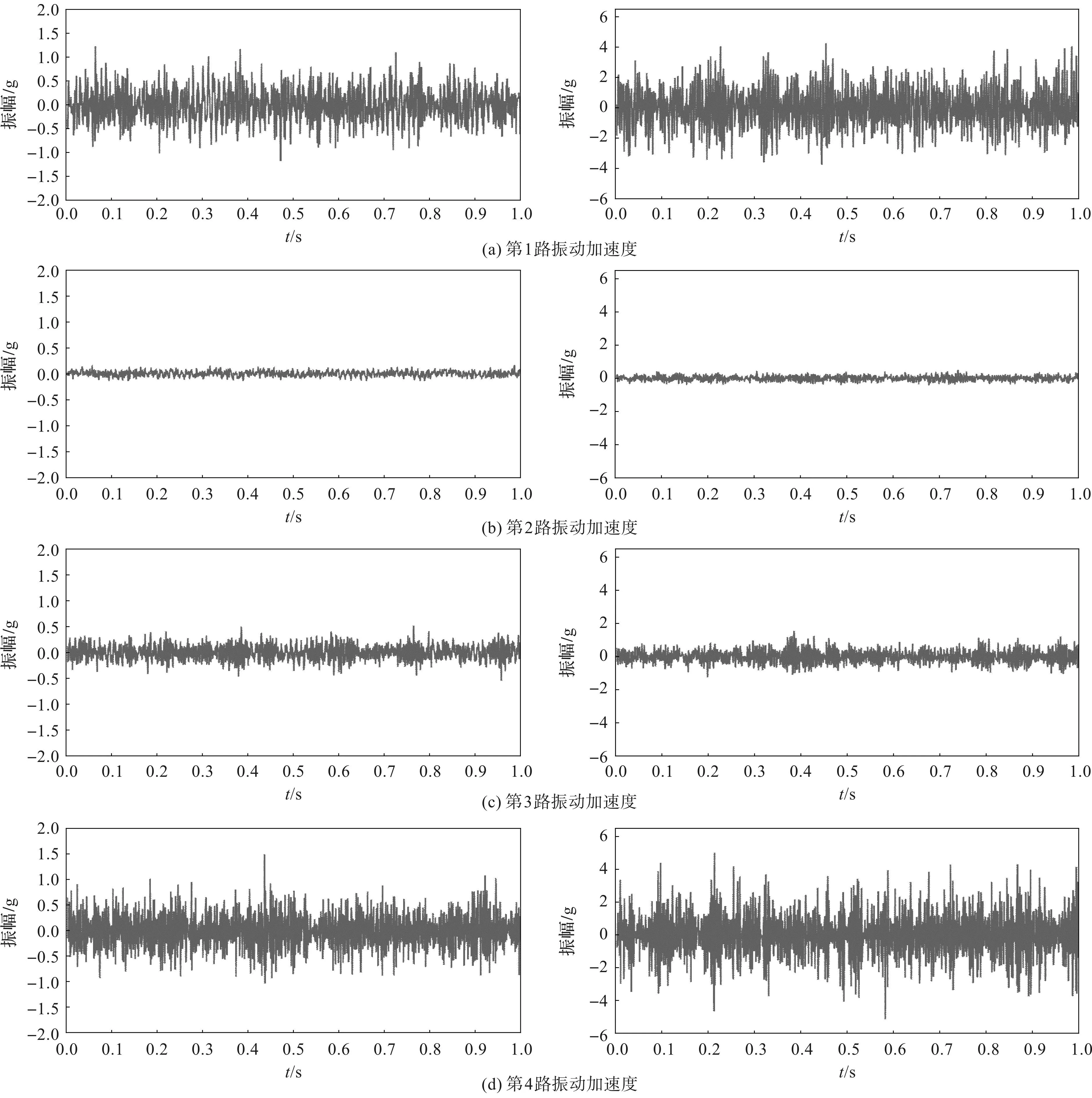
图4 振动信号故障前后时域对比图Fig.4 Time domain comparison of vibration signal before and after fault

由图4可以看出:轴承故障发生后,4路振动信号均呈现出不同程度的幅值变化,其中位于电机输出端的两路振动信号增幅明显,位于电机上平面的振动信号增幅次之,而位于基脚处的振动信号幅值增长幅度最小;同时,不同位置处的振动加速度传感器对于轴承故障的敏感度各不相同,因此依靠其进行故障检测的可信度也不相同。

在不同运行状态下,三相电流信号的时域波形对比图如图5所示。

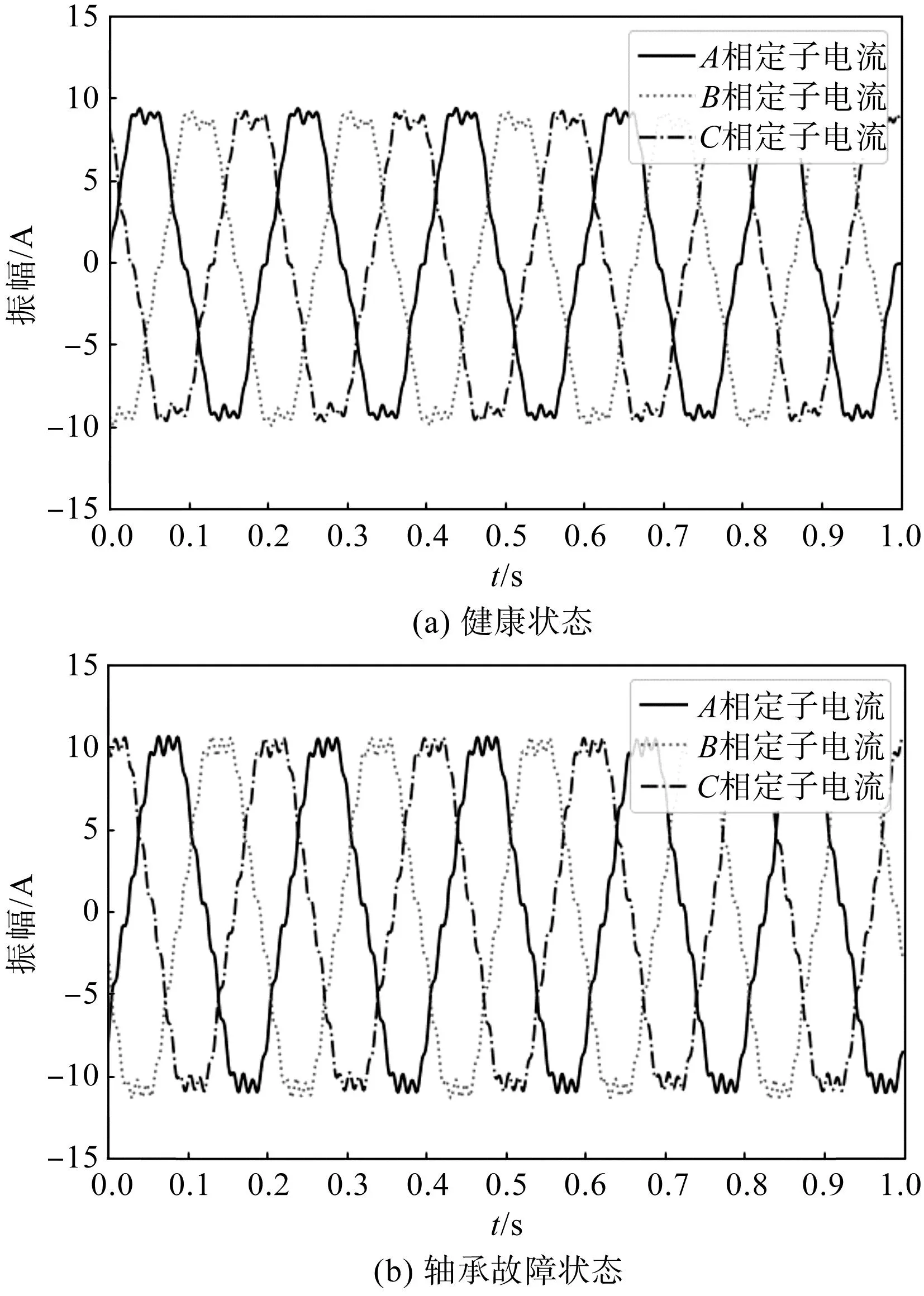
图5 三相电流故障前后时域对比图 Fig.5 Time domain comparison of three-phase current before and after fault

由图5可以看出:当异步电机出现轴承外圈故障后,三相定子电流幅值出现同步增长,且增加幅度基本一致。

振动信号和电流信号均能在一定程度上反映异步电机运行状态。笔者分别对振动信号和电流信号进行时域、频域处理,提取统计特征形成高维混合特征集。其中,时域特征包括最大值、平均值、方差、均方根、标准差、均方根形状因子、方均根值、方均根形状因子、偏度、峰度、波峰因子、纬度因子、脉冲因子;频域特征包括平均频率、频率方差、偏态功率谱、峰度功率谱、频率重心、频率标准差、频率峰度、频率偏度。

此外,笔者将部分电流信号的常用特征一并纳入特征集,包括正序电流、负序电流、三相电流基波分量、正序阻抗和负序阻抗,共得到154维特征。高维度特征集中可能含有部分冗余特征或无关性特征,且会增加训练时间,降低使用效能;因此,需要进行降维处理。

笔者采用mRMR算法对原始特征集进行特征选择。

不同特征集对应的分类准确率如表2所示。

表2 不同特征集尺寸对应分类准确率对照表Table 2 Classification accuracy comparison of different feature sets

表2中列举了分类准确率高于95%的待选特征子集,其中当k=1 733 133时,分类准确率均可达到98%。因此,可以将特征集维度降低至17。

各特征所对应的互信息值如图6所示。

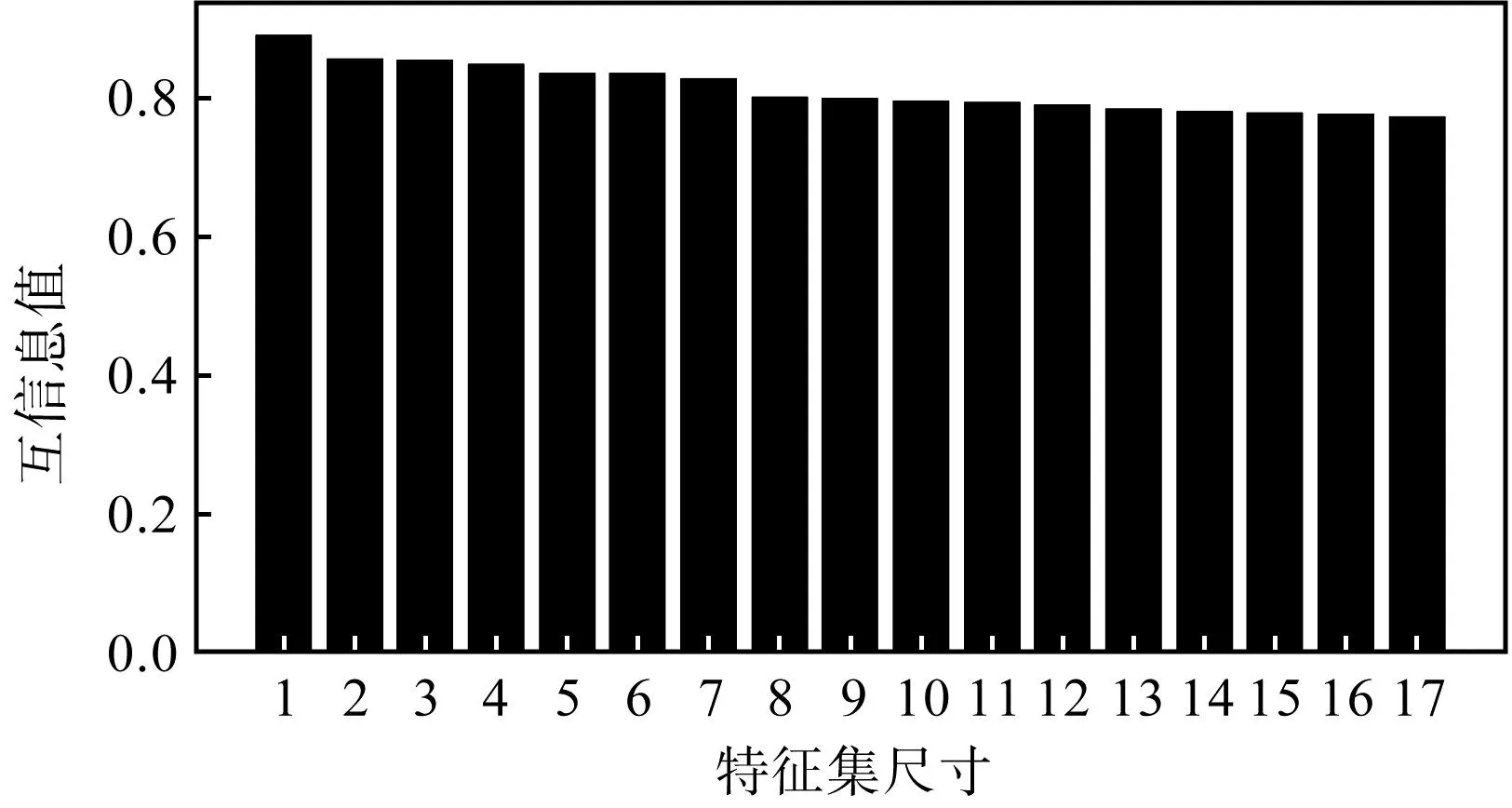
图6 mRMR得到的特征互信息Fig.6 Feature MI by mRMR

由图6可以看出:互信息值各不相同,反映出特征与类标签的相关性不同,不存在同等相关性的特征,即选出的特征间相关度较低。

4 分类结果分析

笔者利用SOM对训练样本进行迭代训练,将样本特征映射到神经网络的不同区域,再将测试样本输入并映射到已经训练完成的SOM平面中,进行故障类型的判别。观察映射区域间的距离可使故障诊断可视化。

以原始高维混合特征集作为输入向量,由此得到的SOM映射结构如图7所示。

图7 原始特征在SOM上的映射与分布Fig.7 Mapping and distribution of original features on SOM

图7分别表示两种状态下的100组训练样本的原始特征和对应的状态标签在SOM上的映射拓扑结构。其中,图7(a)中的数字表示每个被激活的神经元所对应的样本数量,对应于图7(b)的状态标签分布情况。

经过筛选后得到的特征集在SOM上的映射结构如图8所示。

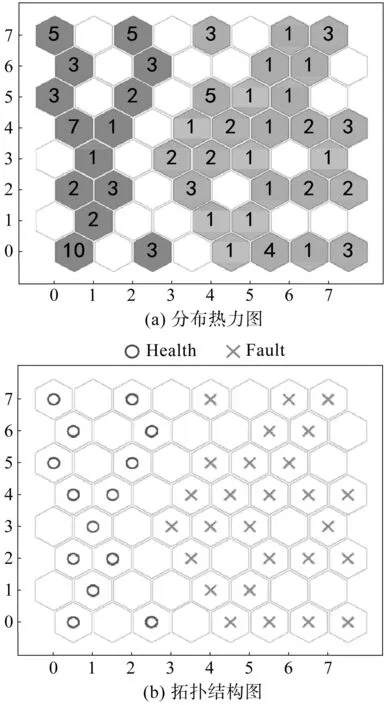
图8 筛选特征在SOM上的映射与分布Fig.8 Mapping and distribution of filtering features on SOM

由图7和图8对比可知:原始特征训练样本在SOM上的分布较为松散,相同状态所代表的神经元之间的关联性不强,电机两种状态间区分效果不明显;经过筛选降维后,特征样本在SOM上的映射更为均匀,且被激活的神经元之间联系紧密,区分效果明显。

笔者使用U-Matrix图表现不同电机状态样本间的距离度量。U-Matrix中的每一个单元格均代表了一种距离度量,这种距离度量根据颜色的深浅进行直观展现,单元格中的颜色越深,代表距离越大,也即两个相邻神经元之间的相似度越差;浅色区域即代表相邻神经元具有高相似度。

笔者将原始特征和筛选后特征的训练样本分别在SOM中训练,得到U-Matrix图如图9所示。

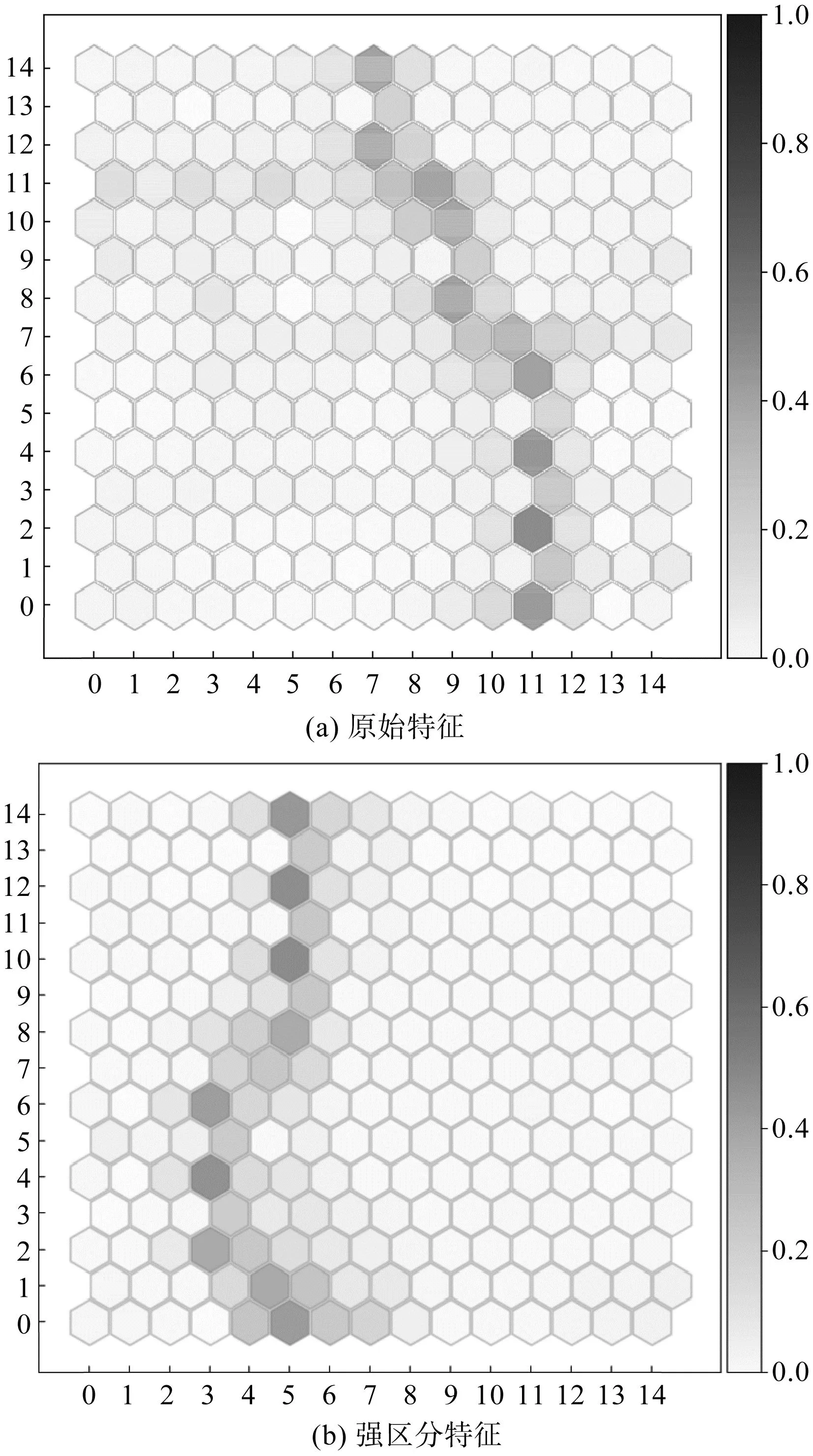
图9 不同特征下的U-Matrix图Fig.9 U-Matrix diagram with different characteristics

图9中,白色区域代表相同状态样本聚集形成的子空间,深色区域则是不同状态间因相对距离较远而形成的分界线。

图9(a)和图9(b)中,两侧白色空间分别对应于图7和图8中对应标签状态的区域,但图9(a)中左侧白色区域中仍存在部分深色区域,影响最终分类效果;图9(b)中左右两侧白色空间深色区域分界线明显,且白色区域内部几乎不存在深色区域,表明SOM在使用筛选得到的特征进行训练后能够获得更好的分类能力,具备更强的状态区分能力。

为了验证测试样本在SOM训练集上的分类效果,笔者使用原始特征和筛选后强区分能力特征,分别对两种电机状态各50组测试样本进行SOM分类。

分类精度和时间参数如表3所示。

表3 特征筛选前后SOM分类准确对比Table 3 SOM classification accuracy comparison before and after feature filtering

由表3可知:笔者使用强区分能力特征进行SOM分类的测试样本明显拥有更好的分类准确精度,且其网络收敛时间缩短23.5%。

笔者将使用筛选后得到的强区分能力特征的测试样本投射到SOM上,并观察其分类情况,得到强区分能力特征测试集U-Matrix分类图,如图10所示。

图10 强区分能力特征测试集U-Matrix分类图Fig.10 U-Matrix classification diagram with strong distinguishing ability features

图10中的“ο”和“×”对应图8中的健康和轴承故障标签,两种状态类别能够从U-Matrix图上进行直观的区分,分类效果十分明显。

图10中,左侧白色子空间即对应健康状态,右侧白色子空间则对应故障状态,两者间由一条深色分界带分隔。但从图10中仍可发现部分测试样本落在深色分界带附近。

为了比较SOM模型的分类性能,笔者分别建立支持向量机分类模型(support vector machine,SVM)和反向传播(back propagation,BP)神经网络分类模型,在相同的训练样本和测试样本下进行识别分类比较,得到了3种网络分类结果,如表4所示。

表4 3种网络分类结果对比Table 4 Comparison of different network

由表4可知:与传统的BP神经网络和SVM相比,基于mRMR-SOM的网络模型具有更高的分类准确精度。

5 结束语

笔者采用了mRMR算法对多信号提取的高维混合特征进行了筛选,并将其作为输入向量,采用SOM进行了异步电机轴承故障诊断,最后根据试验结果对mRMR-SOM方法的有效性进行了验证。

研究结果表明:

1)对比原始特征集和经过筛选的强区分能力特征在SOM上的映射拓扑结构可知,mRMR能够有效保留原始特征集包含的电机状态信息,并可对两种状态进行有效区分;

2)从强区分能力特征的测试集的SOM分类结果看,分类准确率得到了显著提升,达到98%,验证了该方法的有效性;

3)观察保留强区分能力特征的测试集的U-Matrix分类图可以发现,该方法能够明显区分两种状态类别,且分类边界清晰;

4)相比于传统的BP神经网络和支持向量机,SOM拥有更高的分类准确率。

目前,基于mRMR-SOM的诊断方法能够有效解决异步电机轴承故障诊断问题。但异步电机还存在如匝间短路、轴不对中等故障情况,因此,笔者将在后续研究工作中考虑这些情况,以增强该方法的普适性。