基于多域信息融合与深度分离卷积的轴承故障诊断网络模型*

王 同,许 昕,2*,潘宏侠,2

(1.中北大学 机械工程学院,山西 太原 030051;2.中北大学 系统辨识与诊断技术研究所,山西 太原 030051)

0 引 言

轴承是旋转机械装备中最重要的零部件之一。在旋转机械装备中,很多机械装备的失效是由轴承故障引起的,因此,对轴承进行故障诊断是很有必要的[1]。

为了避免轴承故障引起的损失,人们一直在寻找有效的轴承故障诊断方法[2],如各种机器学习算法。利用机器学习算法的轴承故障诊断步骤一般为:先对采集到的信号进行前期的预处理,之后经过人为的挑选特征,将经过一系列处理的数据输入分类器进行识别。

张琛等人[3]对原始信号进行了集合经验模态分解(ensemble empirical mode decomposition, EEMD),将得到的IMF分量依据一定指标筛选重构,结合变分模式分解(variational mode decomposition, VMD)算法得到奇异值熵,并根据其熵值大小判断轴承的故障类别。王望望等人[4]提取了故障轴承的时域、频域、时频域特征,利用核主成分分析(kernel principal component analysis, KPCA)和t-分布领域嵌入(t-distributed stochastic neighbor embedding, t-SNE)算法对其进行了特征筛选,将数据输入K近邻算法(K-nearest neighbor,KNN)分类器中,对轴承故障进行了有效识别。姚德臣等人[5]对故障轴承的信号进行小波降噪后,利用EEMD得到了信号的本征模态函数,提取了多尺度排列熵作为特征,利用支持向量机(support vector machine, SVM)进行了故障分类,在轴承故障诊断方面取得了较好的结果。

上述研究聚焦于传统的机器学习算法,然而机器学习算法繁琐的人工特征提取步骤使其在当今生产业蓬勃发展的大数据时代难以继力[6-7]。繁琐的步骤往往会造成人力、经济、资源等方面的浪费,实用功能欠佳,且相同的特征处理手段在处理不同数据时效果不同。这都是基于机器学习的故障诊断手段面临的难题。

随着近年来计算机技术的发展,深度学习算法应运而生,其自动提取特征的特点深受研究者喜爱[8-9]。深度学习主要的特点是免除了繁琐的人工特征提取步骤,并且达到了更高的准确率。其特点是将预处理信号作为深度学习模型的输入进行自动特征提取,并将提取的特征输送给最后的全连接层,实现分类目的。

在国内外研究中,结合深度学习寻找有效的轴承故障诊断方法成了众多学者研究的热点,许多学者在此方面做了大量工作[10-13]。ZHAO Ming-hang等人[14]提出了一种无需经过信号预处理的基于深度收缩残差网络的故障诊断方法,采用该方法对神经网络块进行了集成,自适应地确定了阈值的策略,实现了较强的特征学习能力,最终在各类型的高振动噪声故障诊断中,展现了较高的诊断精度。CHEN Yue-jian等人[15]提出了一种基于物理信息的长短期记忆网络(long short term memory, LSTM)的超参数选择策略,在变速箱故障诊断中,采用该方法取得了良好的实验结果。XU Zi-fei等人[16]提出了一种多尺度卷积神经网络结合功能注意力机制的模型,该模型有着较好的泛化能力,在轴承故障诊断上有着较高的准确率和较好的稳定性。ZHAO Bo等人[17]提出了一种归一化卷积神经网络,采用批量归一化的操作消除了特征分布的差异,并通过实验验证了该方法的优越性。WANG Duo等人[18]利用元学习和一般的监督学习相混合的方式,考虑了面对少样本数据的故障诊断策略,使用较少的样本对齿轮箱进行故障诊断,取得了较好的实验结果。

笔者研究了这些文献后发现,结合了深度学习的轴承故障诊断方法较之传统方法有更简便的流程以及更高的故障识别准确率。

近年来,研究者们也提出了深度学习融合信号在时域、频域和时频域的故障诊断方法。在轴承故障诊断工作中,对采集到的振动信号进行一定的预处理,往往会挖掘出隐藏在信号中的有用特征。但时域包含的信息有限,使用单一的原始信号要达到更高的识别要求也较为困难。

因此,JIN Yan-rui等人[19]对信号进行了傅里叶变换,将变换后的结果输入残差网络模型,通过在模型中添加注意力机制,取得了比传统残差网络更好的诊断结果。DIBAJ A等人[20]结合VMD和CNN,提出了一种端对端的复合故障诊断方法。MAO Wen-tao等人[21]获取了原信号的时域、频域和时频域信息,结合深度迁移学习策略,使构建的故障诊断模型取得了优异的故障识别结果。CHENG Yi-wei等人[22]构建了一种连续小波变换结合局部二进制卷积网络的故障诊断模型,其利用局部二进制卷积层代替传统卷积层的方法,加快了网路的训练速度,减少了过拟合现象。袁彩艳等人[23]提取了原始信号的多域信息,对传统的残差网络进行了密集式连接,并结合注意力机制对优势特征进行了加权,取得了比传统网络模型更好的轴承故障识别结果。叶壮等人[24]利用经验模态分解算法对信号进行了预处理,将振动信号转换为图像数据,并使用其提出的基于多通道加权的卷积神经网络,充分提取了原信号的多尺度信息,发挥了卷积网络强大的图像特征提取能力。

以上方法在故障诊断领域发挥了一定的作用,但在面临实际工业环境时,仍有以下不足:1)故障诊断准确率较低;2)模型收敛速度不足;3)无法有效平衡模型深度和训练参数量[25-26]。

基于此,笔者提出一种基于多域信息融合结合深度分离卷积(MDIDSC)的轴承故障诊断方法。

首先,考虑到经验模态分解(empirical mode decom-position, EMD)算法模态混叠,且EEMD算法产生的IMF分量仍有噪声混杂情况,采用CEEMDAN算法对信号进行分解,得到原信号的时域空间状态矩阵;然后,利用傅里叶变换和小波变换进一步得到原信号频域和时频域的空间状态矩阵,对各空间状态矩阵进行信息融合后作为神经网络的多通道输入;接着,利用所提出的卷积核深度分离方法对网络进行训练,同时在训练过程中利用自适应学习率退火算法对网络进行优化以避免模型陷入局部最优;最后,引入残差连接以避免网络退化,并利用空间特征提取方法对模型参数进行修剪后分类输出。

1 多域信息融合

1.1 CEEMDAN原理

EMD通过将信号分解为一系列本征模态,表征信号在各个尺度下的信息。但其易产生模态混叠,即IMF分量中包含了多种频率,或一种频率出现在多个IMF分量中。

为解决EMD的模态混叠问题,WU Z等人[27]提出对原信号添加高斯白噪声序列,再对原信号进行EMD分解求平均,但添加的噪声并不能在最后的分解中被完全消除。

CEEMDAN算法在EEMD的基础上进行了优化,该算法流程如下:

步骤1。对信号添加自适应高斯白噪声序列w0*Ni(t),(i∈{1,…,I})。添加了自适应白噪声序列的信号可表示为:

xi(t)=x(t)+w0*Ni(t),(i∈{1,…,I})

(1)

式中:x(t)为原信号;w0为噪声系数;Ni(t)为方差为1的高斯白噪声序列。

步骤2。对添加了自适应噪声序列的信号xi(t)进行EMD分解;对每次分解出的第一个IMF分量求平均得到第一个IMF分量c1(t),其表达式为:

(2)

式中:c1i为每次分解得到的第一个IMF分量。

步骤3。用原信号减去得到的第一个IMF分量,可得残差r1(t),其表达式为:

r1(t)=x(t)-c1(t)

(3)

式中:x(t)为原信号;c1为得到的第一个IMF分量;r1(t)为残差。

步骤4。对得到的残差r1(t)添加自适应噪声序列,得到r1+w1*E1(Ni(t)),再用EMD分解求平均的方式得到第二个IMF分量,其表达式为:

(4)

式中:w1为噪声系数;Ej(.)为一个函数,表示提取EMD分解的第j个IMF。

步骤5。对得到的c2(t)重复上述步骤,依次得到各个IMF分量,直到最后得到的残差不超过两个极值点为止。

最终分解可得n个IMF分量,其表示为[c1,c2,…,cn-1,cn],构建的时域空间状态矩阵如下:

(5)

1.2 多域信息融合原理

为了充分利用原信号携带的信息,笔者提出多域信息融合的理论。该方法结合时域、频域、时频域对信号携带的信息进行表征。

首先,利用CEEMDAN分解时域信号得到各阶IMF分量;然后,利用筛选出的IMF分量构建时域空间状态矩阵;最后,采用傅里叶变换和小波变换得到信号的频域和时频域空间状态矩阵。

笔者对获得的各域空间状态矩阵在通道方向进行融合合并,将合并后的数据作为神经网络的输入进行故障诊断。

笔者对构建的时域空间状态矩阵进行傅里叶变换,得到的频域空间特征矩阵可记为CF,其表达式如下:

(6)

通过对构建时域空间状态矩阵进行小波变换,得到时频域空间特征矩阵可记为CTF,其表达式如下:

(7)

对得到的多域信息CT、CF、CTF进行通道融合,得到信息融合矩阵C,其可记为C=[CT,CF,CTF]。

2 MDIDSC

2.1 深度分离卷积

传统的CNN模型需要进行逐层训练,Inception网络结构使多通道并行卷积成为了现实。笔者提出的深度分离卷积是对Inception网络模型的进一步提升。

Inception网络结构如图1所示。

在笔者提出的深度分离卷积中,传统的3×3、5×5卷积核被深度分离为1×3、3×1,以及1×5、5×1等多个卷积核。经过实验验证,该方法极大减少了训练参数和计算量,并提升了网络训练速度。

由于数据分布存在差异,笔者在该模块中加入批归一化(batch normalization, BN),保证了数据的分布一致性,解决了模型在训练过程中出现的易饱和、信息丢失以及在梯度优化过程中的梯度消失等现象,充分发挥了激活函数的作用。

由于模型深度过深易导致网络退化,笔者设计添加了残差连接,对前层网络提取的特征进行复利用,增强了网络的稳定性。

该模块具体结构如图2所示。

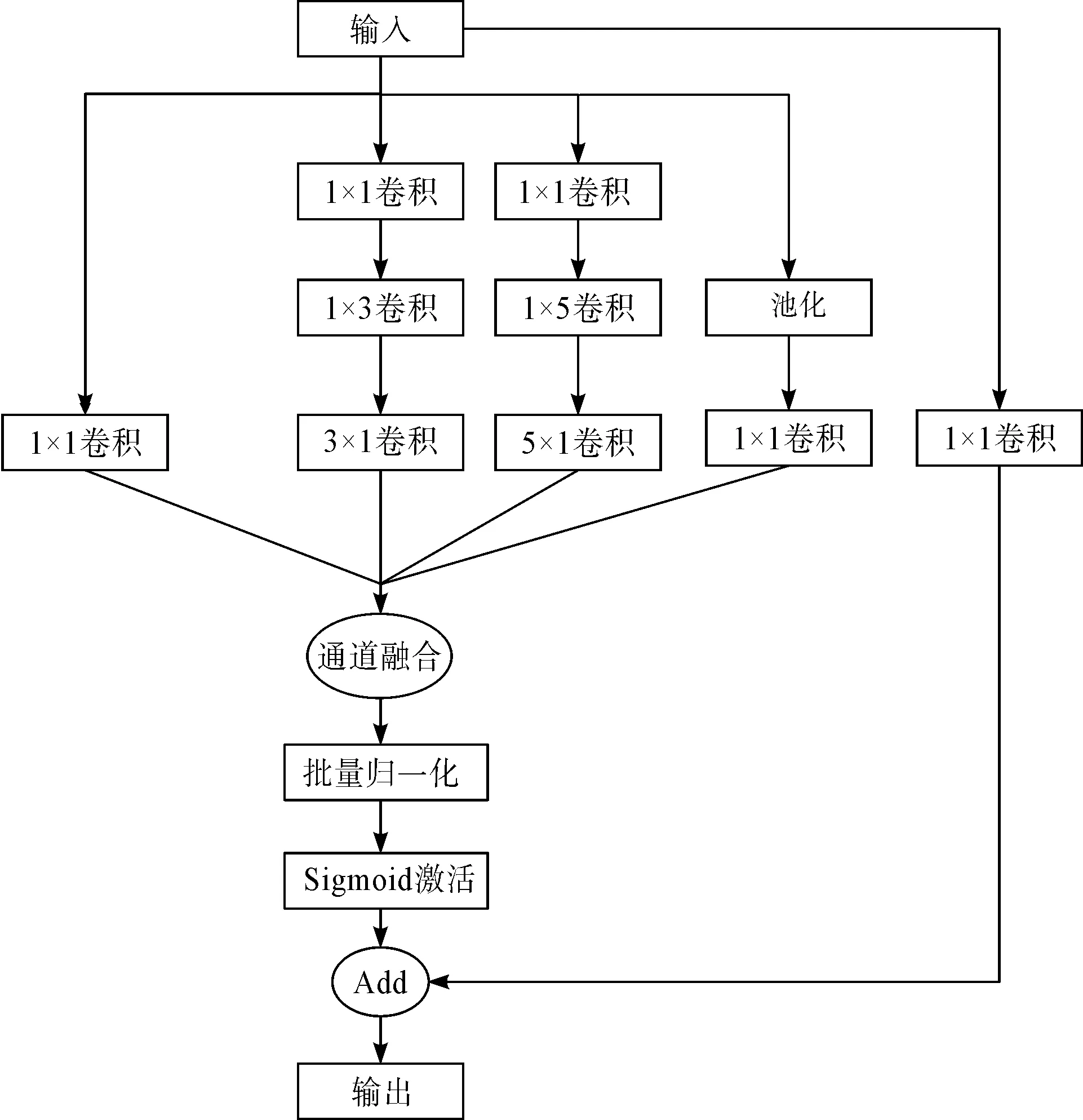
图2 深度分离卷积Fig.2 Depth separation convolutions

2.2 自适应学习率退火

在训练过程中,当训练进行到一定程度,网络训练的准确率将不再上升,损失不再下降,此时网络模型可能陷入了局部最优的情况。为解决该问题,需要对梯度优化时的学习率进行调整。

针对网络易收敛到局部极值点的问题,笔者提出采用自适应学习率退火的方法优化网络训练。该方法通过监测训练时的损失变化,自适应地对学习率进行调节。

其设计思想是对训练损失进行持续监测,当训练损失保持不变持续特定epoch后,优化器的学习率将自适应地减少为原来的1/λ,然后优化器将利用新的学习率进行梯度更新,表达式如下:

lrj=K*lrj-1

(8)

式中:K为学习率衰退因子;lrj为第j次epoch的学习率。

2.3 空间特征提取

将卷积层提取出的特征输入全连接层分类时,过多的参数会导致全连接层训练缓慢,过少的参数则会丢失有用特征。为解决该问题,笔者提出一种对空间特征条件性选取的模型参数修剪方法。

考虑到不同特征图上特征点在通道方向存在分布差异,因而可以对特征图上每个位置的优势特征进行提取,并剔除无效特征以减少参数量和计算量。该方法选择不同特征图上特征点在通道方向绝对值最大的数据作为有效特征,输入全连接层进行分类。

该方法会将多通道特征参数修剪为一个特征图大小,并最大程度保留原始数据的特征信息,其表达式如下:

(9)

空间特征提取操作对冗余特征进行剔除,减少了网络结构的总参数量。

3 实验验证

为充分验证MDIDSC的有效性,笔者采用了两类不同的数据集进行了对比实验。第一类是由西安交通大学转子轴承实验室提供的滚动轴承加速寿命实验数据[28];第二类是由美国凯斯西储大学提供的滚动轴承振动信号数据。

笔者在这两种轴承故障数据集上,从数据分析、数据预处理、故障诊断实验结果分析、不同方法对比等方面展开讨论。

3.1 西安交通大学数据集实验

笔者首先利用西安交轴承数据集进行实验。

该数据集有着丰富的轴承故障信息,其实验平台由两个振动加速度传感器(一个水平和一个竖直方向)、实验轴承、交流电动机和电机转速控制器等设备组成。

该实验平台具体信息如图3所示。

图3 西安交通大学轴承实验平台Fig.3 Xi’an Jiaotong University bearing experimental platform

3.1.1 数据故障信息

笔者对西交轴承数据集进行分析,采用传感器位于水平方向获得的振动数据进行实验。

笔者设置了外圈故障、保持架故障、内外圈故障、内圈故障、多种复合故障等5种故障类型。

各故障轴承如图4所示。

图4 实验故障状态轴承Fig.4 Fault state bearing

每类故障共设置100个样本,所有样本的采样频率均为25.6 kHz。其中,总样本的80%用于测试,20%用于验证,每个样本共含数据点1 024个。

具体轴承故障信息参数如表1所示。

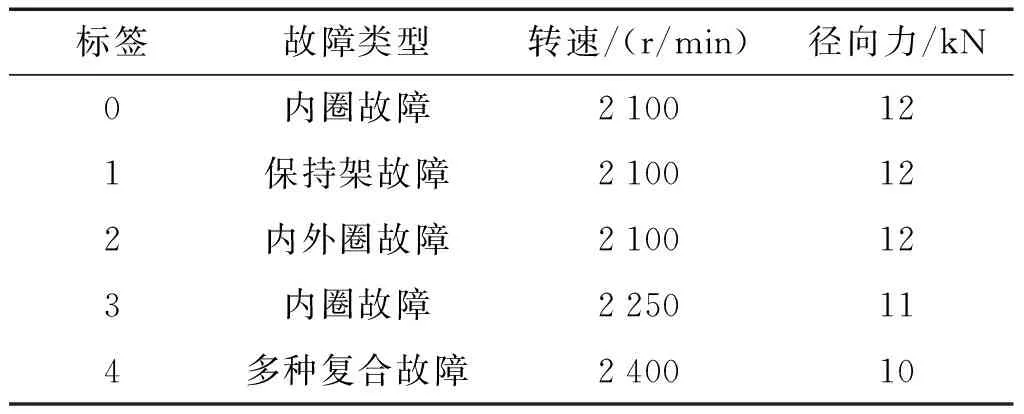
表1 具体故障信息和分类标签Table 1 Specific fault information and classification label

3.1.2 信号预处理

笔者先对故障信号进行分解变换,获得了时域、频域和时频域空间状态矩阵,然后对获得的多域空间状态矩阵进行通道信息融合,最后将该多通道数据输送至神经网络进行训练[29-32]。

为充分表征选取的故障轴承状态信息,笔者绘制了选取的5种故障类型的时域信号图形。

各故障类型的时域信号如图5所示。

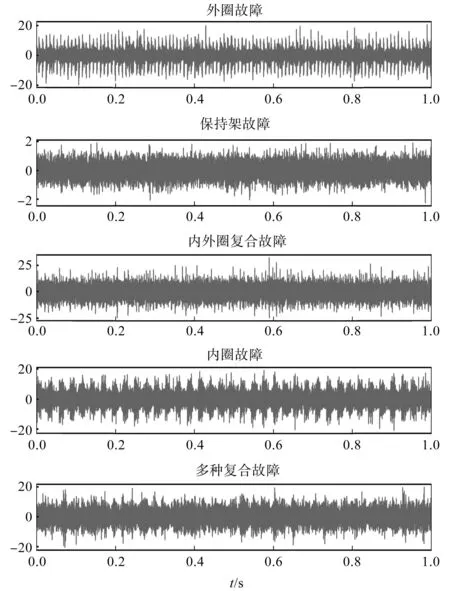
图5 各类型故障信号图Fig.5 Each type of fault signal

笔者选取了分解的前5个IMF分量构建空间状态矩阵。这些内圈故障振动信号的IMF分量如图6所示。

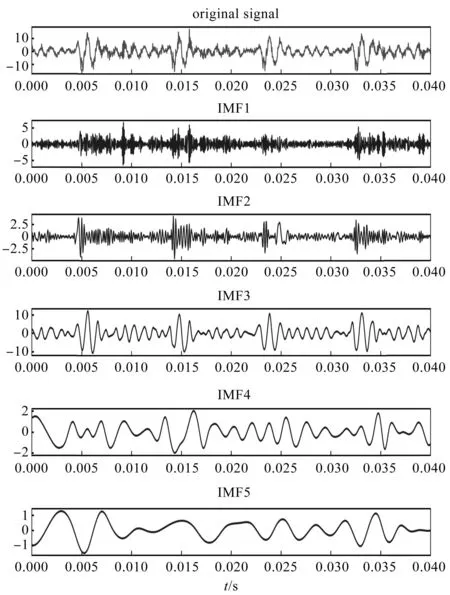
图6 内圈故障IMF分量时域图Fig.6 IMF time domain diagram of inner ring fault

笔者选取CEEMDAN分解出的前5个IMF分量构建了时域空间状态矩阵,然后利用傅里叶变换、小波变换,对时域IMF分量构建的时域空间状态矩阵进行变换,分别得到频域空间状态矩阵和时频域空间状态矩阵。

3.1.3 笔者所提模型结构

笔者先利用CEEMDAN算法对原始信号进行分解,然后利用傅里叶变换和小波变换分别构建时域、频域和时频域空间状态矩阵,对得到的3个空间状态矩阵进行通道融合,并将其输入网络进行训练。

笔者在网络中依次进行卷积、批量归一化、最大池化和Sigmoid激活,将初步训练后的数据送入特征提取优化模块提取特征;利用特征提取优化模块重复计算3次后进行卷积、批量归一化等操作;最后对得到的多通道特征图进行参数修剪并输入全连接层进行分类输出。

总体网络结构流程图如图7所示。

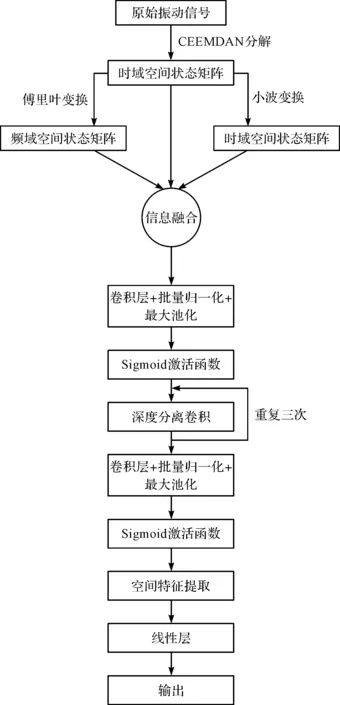
图7 网络结构Fig.7 Network structure

3.1.4 实验结果

为充分验证MDIDSC的正确性,笔者记录了在网络训练中测试集和训练集准确率和损失的变化。

实验结果如图8所示。

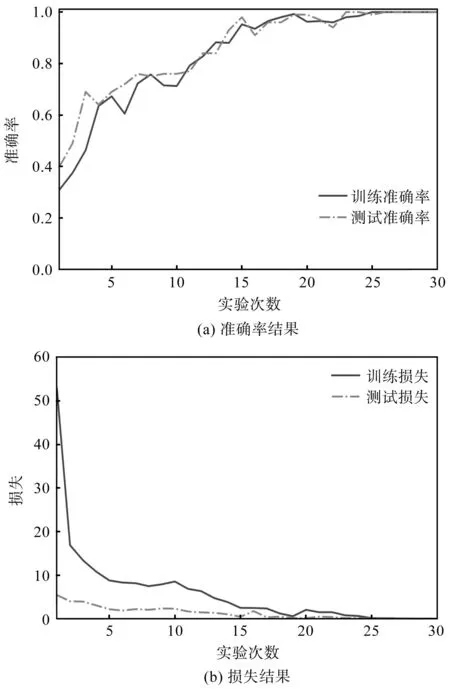
图8 准确率和损失变化Fig.8 Change of accuracy and loss

由图8可以看出:MDIDSC在训练一开始损失较大、准确率较低;但随着实验进行,当训练到25代左右,MDIDSC便基本达到收敛,此时损失和准确率不再变化,准确率最高为100%。

该实验结果验证了笔者方法的有效性和稳定性。

为进一步展示实验结果,笔者绘制了某次实验中测试集的混淆矩阵输出结果。

该混淆矩阵结果如图9所示。

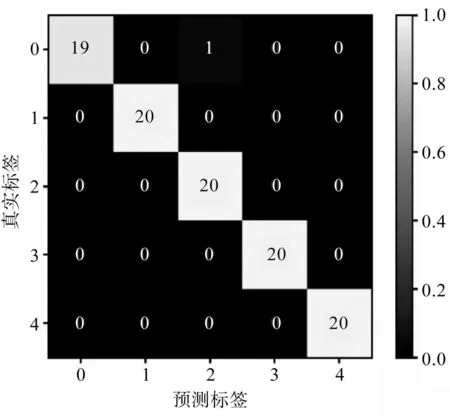
图9 某次测试集混淆矩阵Fig.9 Confusion matrix of certain test set

由图9混淆矩阵所示:在该次实验中,对于测试集的100个样本,仅有1个内圈故障被分类为内外圈复合故障,剩余所有样本均分类正确。

笔者利用t-SNE算法对输出特征进行了降维可视化,该可视化结果与混淆矩阵输出结果基本一致。

可视化结果如图10所示。

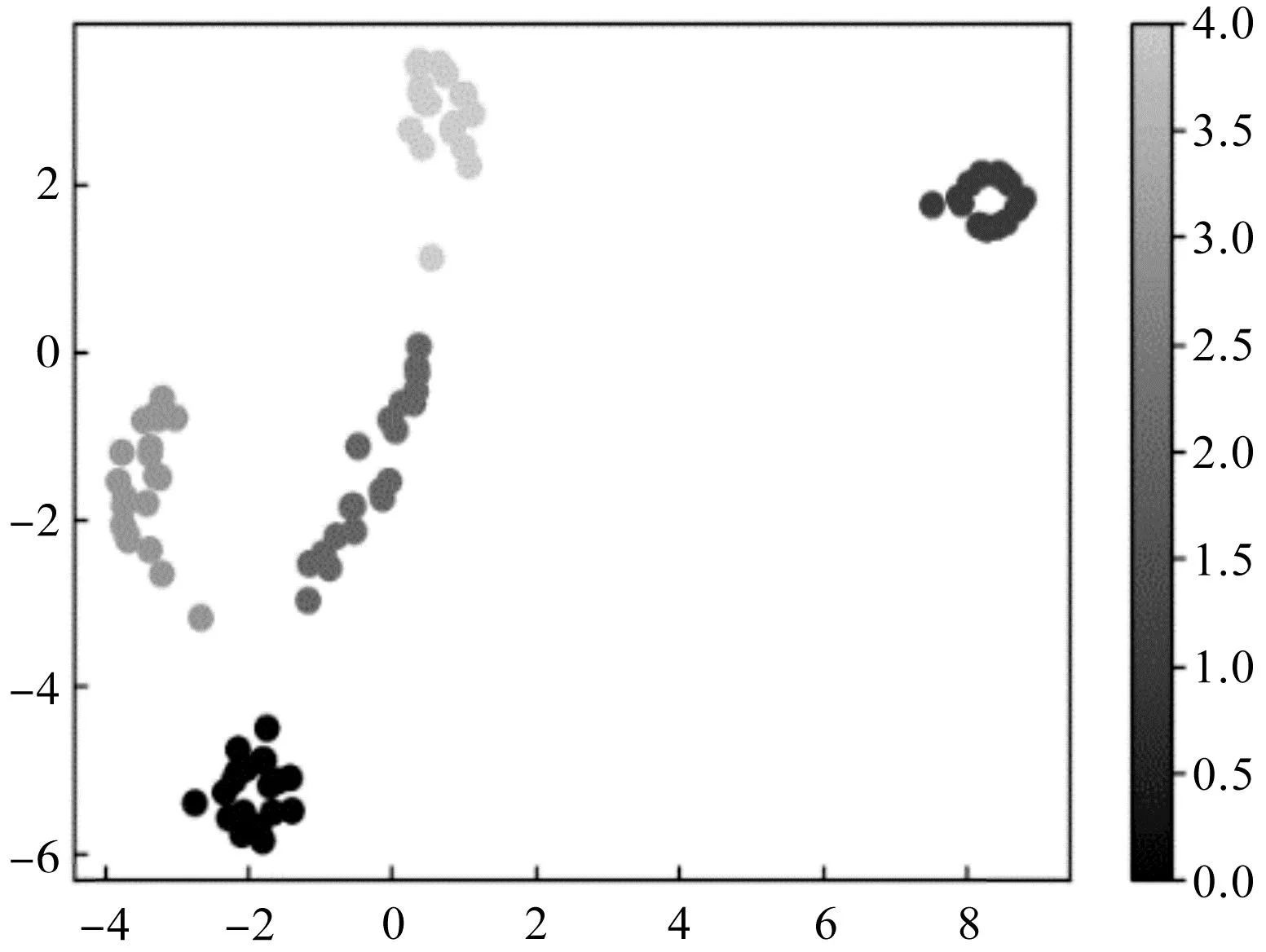
图10 某次测试集可视化Fig.10 Visualization of certain test set

3.1.5 不同方法对比

笔者选取了较为常用的一些故障诊断方法与MDIDSC进行了对比。选择的对比方法分别为Inception、残差网络(residual neural network, ResNet),以及近年来机器学习中较为流行的轻量级梯度提升机器学习(light gradient boosting machine,LGB)算法。

为保证对比实验的公正性,笔者选取的Inception网络模型和残差网络模型均具有与MDIDSC一样的网络深度和输入。同时,为了突出MDIDSC的特点,Inception网络模型没有进行残差连接,残差模型没有通道分离操作。为了更好地进行比较,2种方法都没有对卷积核进行深度分离。

最后,笔者选取了没有通道分离和残差连接的LGB算法,为进一步提高LGB算法的性能,在LGB分类前利用主成分分析(principal component analysis, PCA)对输入数据进行了降维。

各方法的对比结果如图11所示。

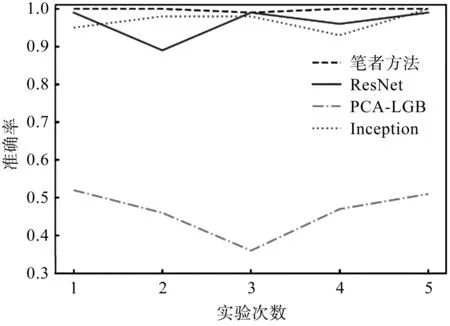
图11 不同方法对比Fig.11 Comparison of different methods

由图11可以看出:MDIDSC有着较高的准确率和较好的稳定性;Inception模型和ResNet模型准确率略高,且测试结果不够稳定;PCA-LGB方法在该数据集上的准确率较低。

3.2 凯斯西储大学数据集实验

为充分验证MDIDSC的有效性,笔者利用凯斯西储大学提供的轴承数据集对所提方法做了进一步检验。该数据集的实验平台由一个2马力的电动机、滚动轴承、扭矩传感器、功率测试计及控制器等组成。

实验台如图12所示。

3.2.1 数据故障信息

通过对凯斯西储大学的轴承数据集进行分析,笔者选取了加速度传感器位于电机壳体垂直向的驱动端获得的振动数据进行实验论证。该实验中,轴承外圈故障频率为104.56 Hz,内圈故障频率为157.94 Hz,滚动体故障频率为137.48 Hz。

笔者共选取了7种不同类型的轴承故障数据进行实验,各故障类型分别为内圈故障(负载分别有0 W、735 W两种)、外圈故障(负载0 W、735 W两种)、滚动体故障(负载0 W、735 W两种)和正常状态。每种故障类型的轴承损伤直径统一为0.177 8 mm。

笔者选取的具体轴承故障信息参数如表2所示。

表2 故障状态信息和分类标签Table 2 Fault status information and classification label

每种故障类型包含有100个样本,总数据包含有700个样本。该数据的采样频率为12 kHz,其中总样本的80%用于测试,20%用于验证。每个样本包含的原始振动信号数据点个数为1 024个。

3.2.2 信号预处理

针对每种故障状态信息,笔者绘制了所选取的各类轴承故障的时域信号。

笔者选取的各类轴承故障的时域信号如图13所示。

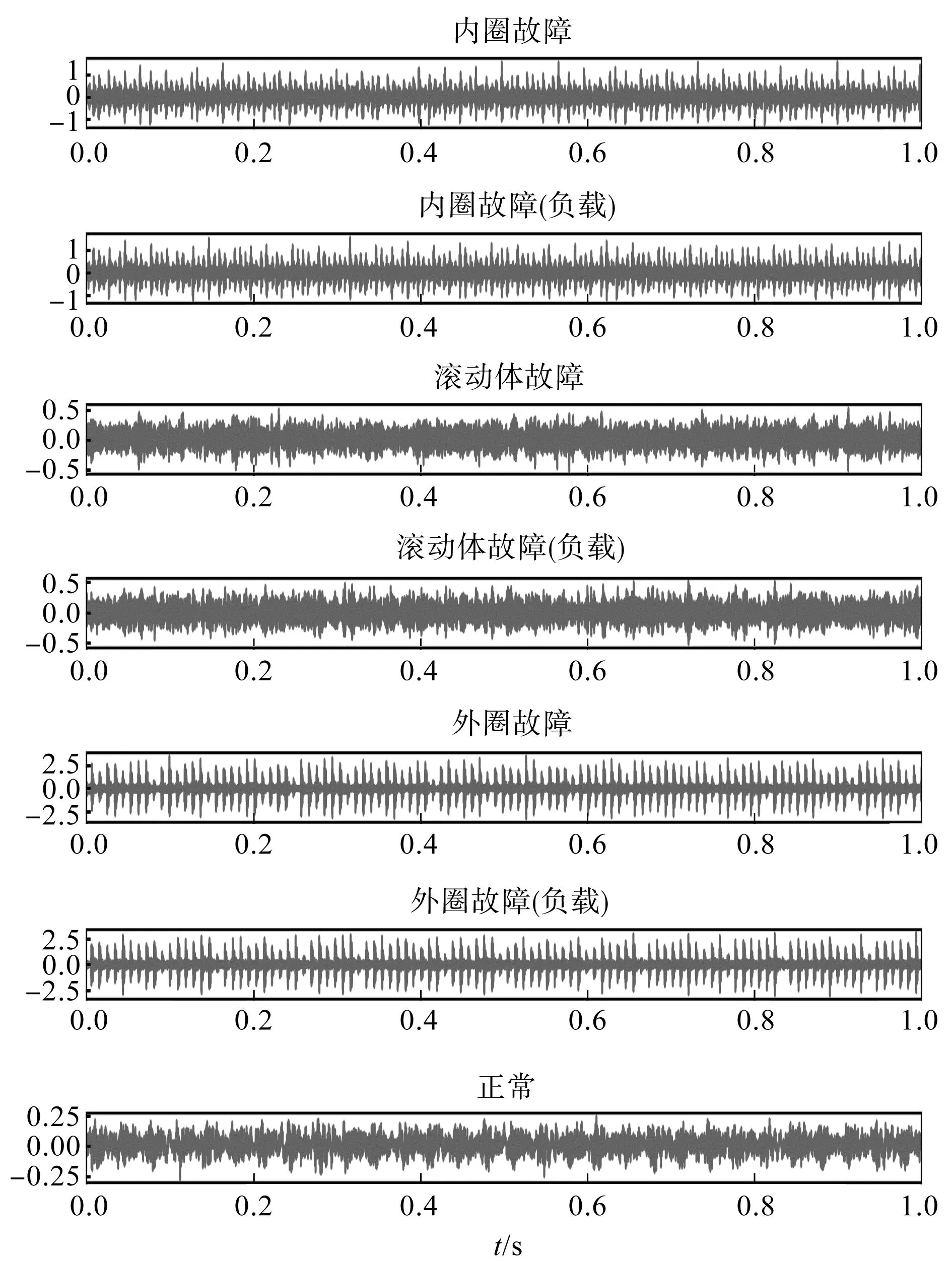
图13 各故障信号图Fig.13 Each type of fault signal

笔者选取了分解得到的前5个IMF分量进行空间状态矩阵的构建,并选取内圈故障振动信号的IMF分量进行展示。

内圈故障振动信号的IMF分量如图14所示。

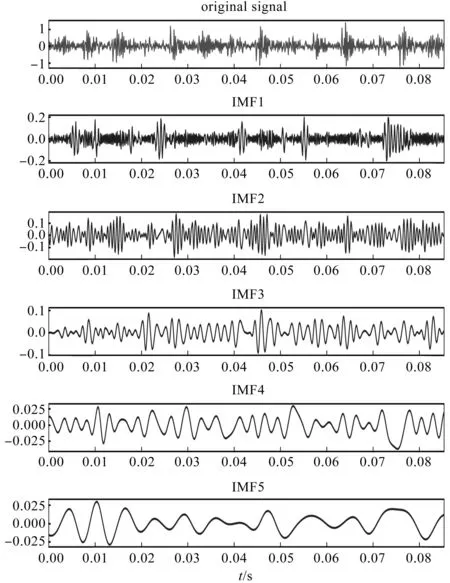
图14 内圈故障IMF时域图Fig.14 IMF time domain diagram of inner ring fault

笔者选取CEEMDAN分解出的前5个IMF分量构建时域空间状态矩阵,然后分别利用傅里叶变换、小波变换对所得的时域空间状态矩阵进行时频变换,最终得到该数据集下的频域空间状态矩阵和时频域空间状态矩阵。

3.2.3 实验结果

为在该数据集上充分验证MDIDSC的优越性,笔者进行了10次测试实验,分别记录了在10次实验中训练集准确率和测试集的损失以及准确率的变化。

实验结果如图15所示。

由图15结果可知:在对该轴承数据集的10次轴承故障诊断实验中,训练集故障识别准确率最高为100%、最低为99.64%,平均为99.95%;测试集故障识别准确率最高为100%、最低为98.57%,平均为99.07%。训练集的最大损失为0.290 0,最小为0.026 2,平均为0.075 8;在测试集中的最大损失为0.134 5,最小为0.053 2,平均为0.084 1。

为进一步展示针对MDIDSC的实验结果,笔者绘制了某次实验中测试集混淆矩阵的结果,其中横轴代表神经网络的预测值,纵轴代表真实值。

该混淆矩阵如图16所示。

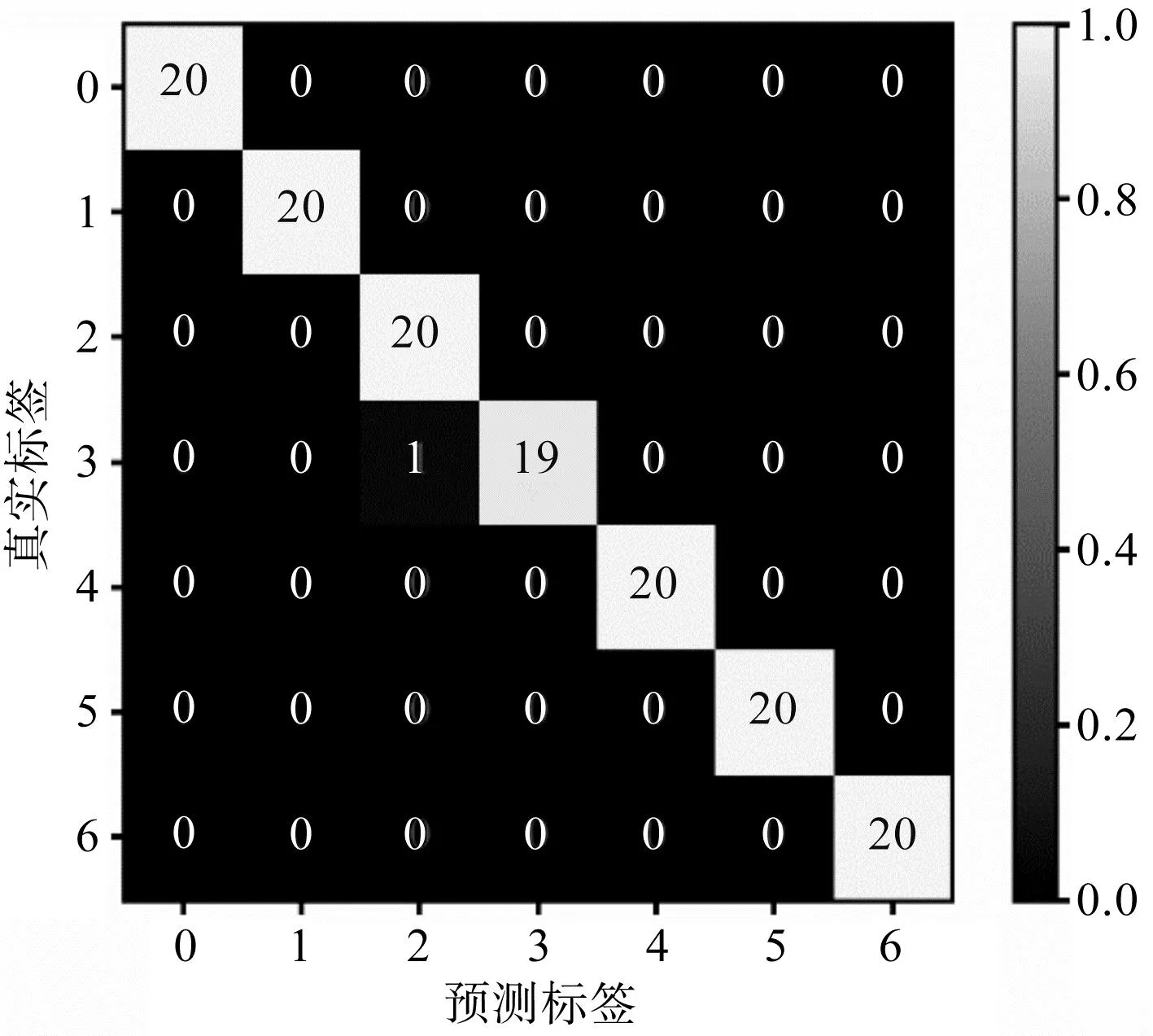
图16 某次测试集混淆矩阵Fig.16 Confusion matrix of certain test set

由该混淆矩阵可知:该次实验中,测试集的140个样本里仅有一个735 W负载的滚动体故障被误分类为无负载的滚动体故障,剩余所有数据均分类正确,测试准确率为99.29%。

笔者利用t-SNE算法对输出特征进行了降维可视化处理,该可视化结果与混淆矩阵输出结果基本一致。

可视化结果如图17所示。

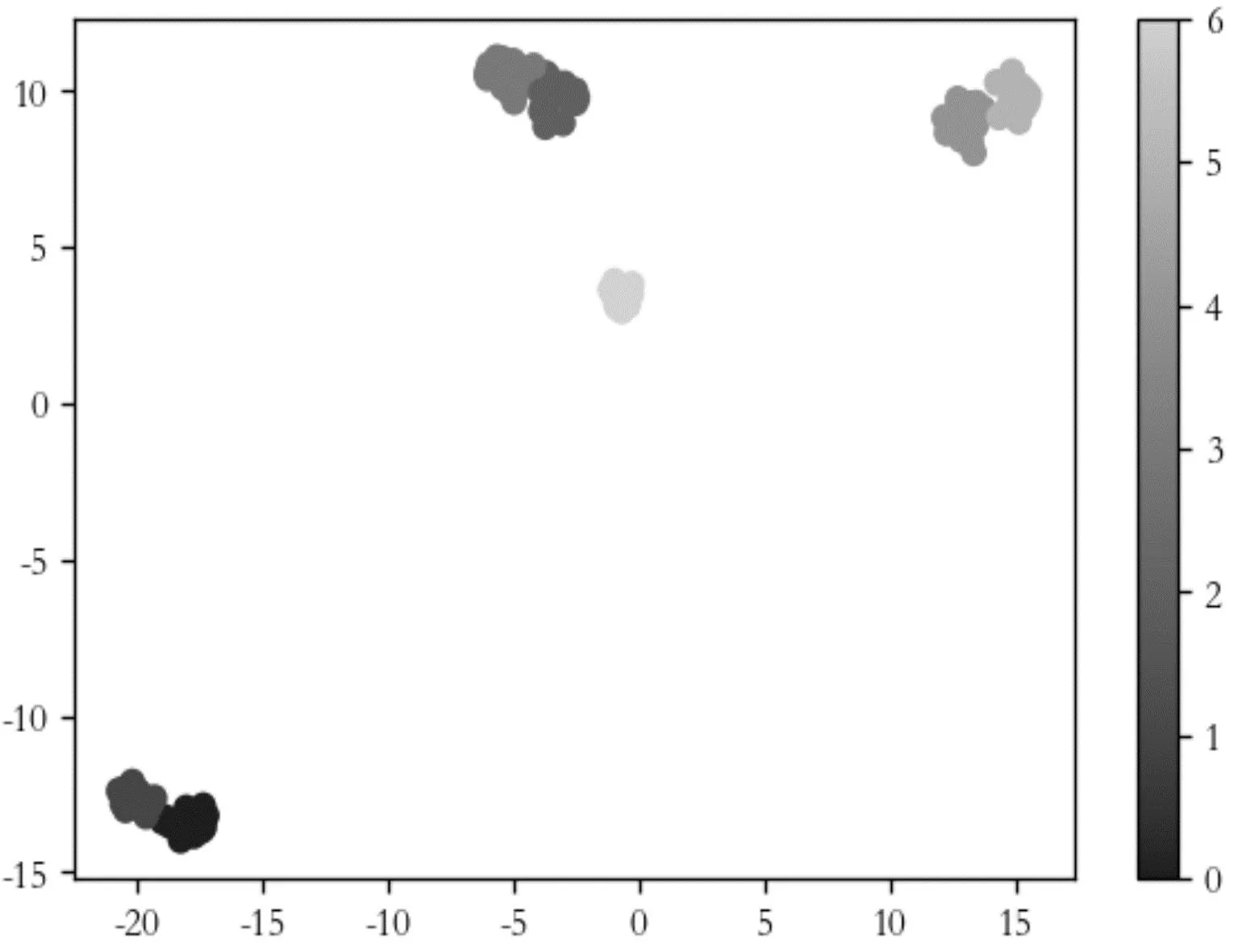
图17 某次测试集可视化Fig.17 Visualization of certain test set

3.2.4 不同方法对比

笔者在该数据集上也设置了多组对比实验,选择的对比模型为Inception网络、ResNet以及PCA-LGB算法。

最终的实验结果如图18所示。

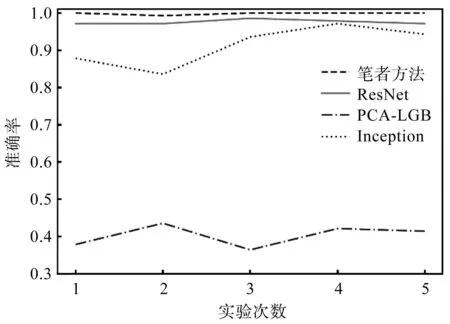
图18 不同方法对比Fig.18 Comparison of different methods

由图18可以看出:MDIDSC有着较好的稳定性和较高的准确率;ResNet的准确率和稳定性都稍逊于笔者方法;Inception和PCA-LGB算法在该数据集上的准确率较低,且不够稳定。

4 结束语

考虑传统CNN网络在网络过深时会出现参数过多、计算量过大、特征信息丢失以及训练过慢的情况,笔者提出了一种用于轴承故障诊断的网络模型。

首先,利用CEEMDAN对信号进行了分解,并采用傅里叶变换和小波变换获得了信号的多域信息;然后,采用卷积核深度分离的方法进行了特征提取;采用学习率退火和参数修剪的方法对网络模型进行优化;最后,通过实验对MDIDSC的优越性进行了验证。

研究结果如下:

1)多域信息通道融合方法丰富了数据特征,提升了神经网络的泛化性和鲁棒性,其在实验中的最高测试准确率可达100%;

2)深度分离卷积模型减少了网络模型的总参数,同时使用残差连接对网络特征进行了复利用,MDIDSC仅在一类数据上的准确率为99.29%,在其他类别数据上的预测准确率均为100%;

3)自适应学习率退火梯度和参数修剪的网络优化训练方法,加速了网络的收敛,同时避免了网络易收敛到局部极值点的问题,在凯斯西储轴承数据集上的平均测试准确率为99.95%。

在后续研究中,笔者将聚焦于小样本和样本不平衡的旋转机械故障诊断问题;同时拟增加抗噪模块,以进一步提高该网络模型在不同工况下的普适性。