仿真数据驱动的起重机钢丝绳断丝定量识别方法*
王晓昆,井陆阳*,白晓瑞,战卫侠,刘云成,王彦松
(1.青岛理工大学 机械与汽车工程学院,山东 青岛 266520;2.海军工程大学 兵器工程学院,湖北 武汉 430032;3.软控股份有限公司,山东 青岛 266000)
0 引 言
在工程起重机设计过程中,起重机钢丝绳通常是其关键的承载和牵引构件。由于其所处的工况条件复杂、工作环境恶劣,易产生一些损伤,存在严重的安全隐患[1]。
断丝作为钢丝绳服役期间极易产生的主要损伤,是影响钢丝绳安全运行的重要因素。在国标中,将一个捻节距内断丝数占钢丝绳总丝数的比例作为报废的重要指标。因此,对钢丝绳断丝数进行准确检测已成为急需解决的问题[2]1-3。
目前,电磁检测法被公认为是对钢丝绳进行无损检测最有效的方法。基于漏磁法的钢丝绳断丝损伤定量识别,实质上是建立损伤信号的特征信息与损伤程度的空间映射分类准则。近年来,研究人员用机器学习模型,解析了不同类型损伤信号的特征信息与损伤程度之间的非线性映射关系,取得了较好的断丝识别效果[3-6]。
赵志科等人[7]为了进一步提高极限学习机(extreme learning machine,ELM)的分类精度,提出了一种可变步长增量式极限学习机(variable step incremental extreme learning machine,VSI-ELM),其利用加州大学欧文分校提供的样本集对ELM算法进行了性能测试,通过回归和分类实验分别研究了VSI-ELM模型的性能。张东来等人[8]提出了钢丝绳断丝定性和定量分级检测的方案,对于定性检测,输入层和隐含层之间用小波函数作为权系数,两层之间无非线性,适于定性分类;对于定量检测,则应用小波非线性,神经网的输入是特征向量和小波的内积,适于特征与断丝程度之间定量关系的逼近。LI X等人[9]针对钢丝绳漏磁(magnetic flux leakage,MFL)测试中信号去噪效果差、识别率低、实时性差等问题,提出了一种核极限学习机(kernel extreme learning machine,KELM)与压缩感知相结合的新算法,其将正则化的正交匹配追踪(regularized orthogonal matching pursuit,ROMP)引入压缩传感小波(compre-ssed sensing wavelet,CSW),并结合了双密度小波变换(double-density wavelet transform,DD-DWT)以提高钢丝绳信号降噪的效果,最后利用KELM提高了钢丝绳定量识别的检测精度和效率。
然而,以上这类断丝定量识别方法往往需要大量的损伤数据对模型进行训练,而在实际工程中,由于现代机械制造设备技术的进步、维护水平的提升,以及机械设备大多时间处于正常运行的状态,导致钢丝绳故障信号的采集难度较大,进而对断丝定量识别准确率产生较大影响[10]。
仿真数据驱动的模式识别方法是解决故障样本不足的一种有效途径,在轴承等机械设备故障诊断领域有一定的应用。而目前为止,该方法在钢丝绳故障诊断方面的相关研究极少。因此,笔者对钢丝绳断丝定量识别应用仿真数据驱动的方法展开了一系列研究[11-13]。
首先,笔者使用有限元软件对不同损伤类型钢丝绳进行仿真,得到仿真数据;然后,使用钢丝绳漏磁检测实验台采集与仿真时损伤类型相同的实测数据;针对实验采集过程中存在噪声等因素干扰导致其与仿真数据不匹配的问题,采用小波变换的方式对实测数据进行去噪;最后,建立卷积神经网络(CNN)模型,采用仿真数据辅助模型训练,并使用早停法抑制模型对训练集中仿真数据的过拟合问题。
模拟实际工况分别采用无实测样本和少量实测样本两种实验形式进行验证,在无实测样本工况下,仅使用仿真数据训练CNN模型;在少量实测样本工况下,使用仿真数据辅助小波去噪处理后的小样本实测数据作为CNN模型的训练集。
1 理论背景
1.1 永磁励磁原理
永磁励磁方式在漏磁检测中应用较为广泛,其基本原理如图1所示。

图1 漏磁检测原理Fig.1 The principle of magnetic flux leakage detection
钢丝绳在励磁器中被永磁铁磁化至饱和后,衔铁、永磁体、空气隙和钢丝绳形成闭合磁路。在钢丝绳无损伤时,磁感应线会在钢丝绳内部平行且均匀通过,理想情况下泄露的磁通量基本为零,如图1(a)所示;当钢丝绳表面出现断丝损伤时,受损部位钢丝会出现断口,由于损伤部位的磁阻增大,而空气的磁导率很小,部分磁感应线会泄漏到空气中形成漏磁场,如图1(b)所示。
通过检测距损伤部位一定提离值处的磁感应强度大小,从而可以实现损伤的检测的目的[14]。
1.2 有限元仿真原理
COMSOL Multiphysics是一款应用广泛的高级数值仿真软件。为了分析涉及静态和低频范围的电磁系统和过程,其内含的AC/DC模块通过求解麦克斯韦方程,将工程中的电磁场计算转变为庞大的矩阵求解。
在对钢丝绳不同损伤的漏磁场分析中,采用有限元数值仿真的方法,可以模拟任意尺寸的励磁检测器以及任意类型的损伤,其具有较大的灵活性。因此,可使用有限元软件进行仿真实验,得到所需损伤数据。
1.3 卷积神经网络
卷积神经网络是一种深度前馈神经网络,其典型结构由输入层、卷积层、池化层与全连接层构成。一维卷积神经网络是指在一维数据上进行卷积和池化等操作。
卷积神经网络结构如图2所示。

图2 卷积神经网络结构Fig.2 Convolutional neural network architecture
CNN实际上是通过建立多个滤波器来提取数据的局部特征。多网络层数可提取到更深层次的数据特征,最后得到具有平移旋转不变性的鲁棒特征。
当断丝漏磁发生时,仿真与实验在此处采集的磁场密度值都会增大,其表现出明显的局部空间特性。利用CNN可有效提取其局部特征,完成数据的收敛分析工作[15-18]。
2 钢丝绳断丝仿真与实验
2.1 仿真损伤信号
笔者使用COMSOL有限元软件对钢丝绳损伤进行仿真的流程如图3所示。

图3 仿真流程Fig.3 Simulation flow
首先,笔者选择AC/DC模块中的磁场、无电流物理场,按照设计尺寸对永磁励磁装置和钢丝绳进行建模;然后,定义材料和边界条件并划分网格,再进行求解器配置后验证模型并求解;求解完成后,可以根据需要查看磁力线、磁场强度、磁场密度等电磁参数,并进行下一步分析。
2.1.1 钢丝绳永磁励磁装置建模
笔者利用COMSOL有限元软件的建模功能对钢丝绳永磁励磁装置进行建模。根据漏磁原理可知,钢丝绳被磁化后,当内部磁感应强度较低时,不容易产生漏磁场,而钢丝绳磁化饱和后才能产生较多的漏磁。
直径24 mm的6×37+FC(FC表示钢丝绳的绳芯是纤维绳芯)结构钢丝绳,单丝直径1.1 mm,破断负荷为358 kN,其主要用于各种起重、提升和牵引设备,且其具有良好的磁化效果。因此,笔者选择实验钢丝绳为6×37+FC结构的直径24 mm钢丝绳,衔铁材料选择磁导率、饱和磁导密度都较高的工业纯铁DT4,磁铁材料为汝铁硼材料N35。
永磁励磁装置采用多回路周向励磁的方法,永磁铁做成环状放置在励磁器两端,衔铁做成管状以最大限度的减少漏磁[19]。
其具体结构如图4所示。
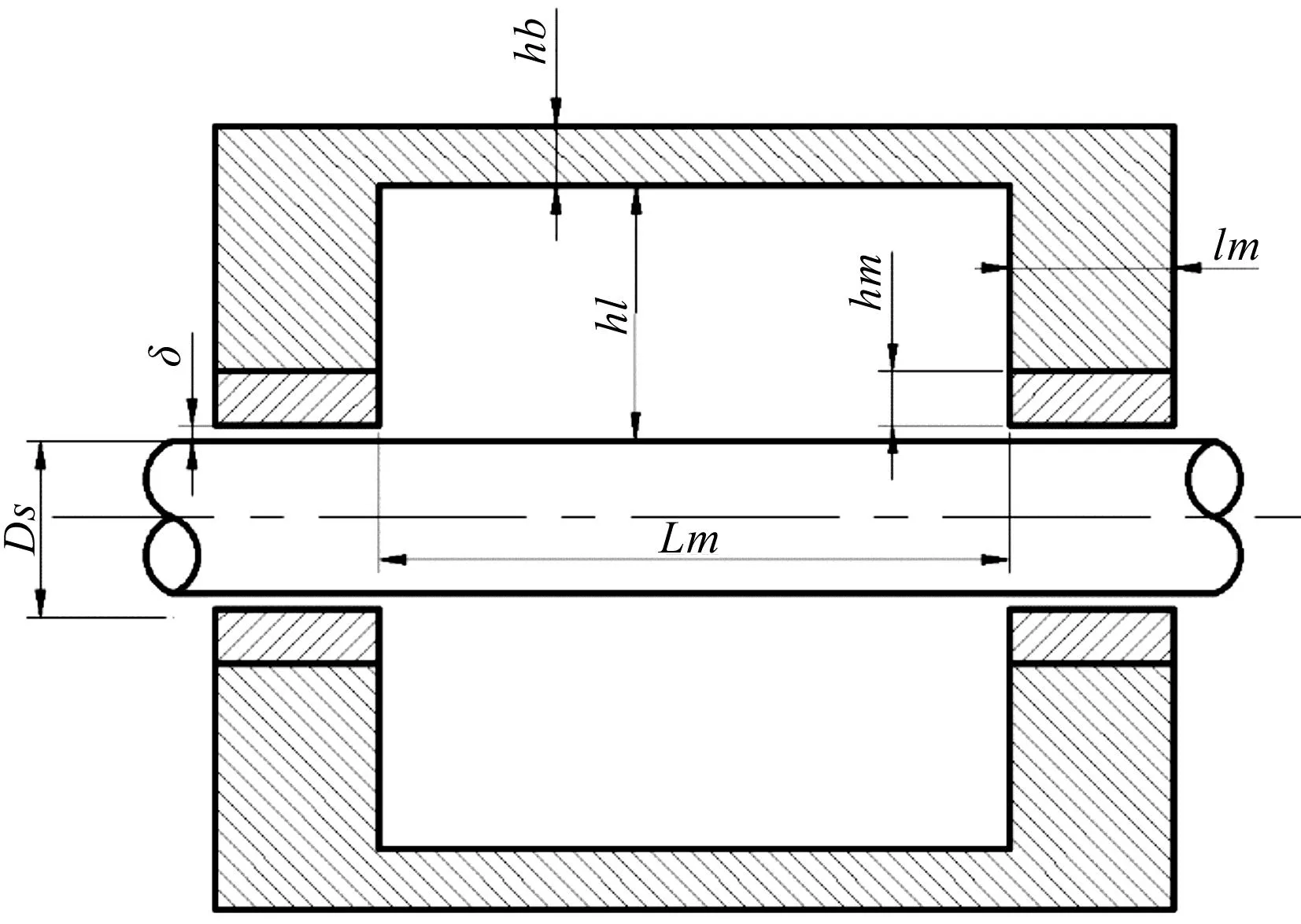
图4 励磁器结构Fig.4 Exciter structureDs为与钢丝绳有效金属面积相等的钢绞线直径;lm为永磁体沿钢丝绳轴向的长度;δ为永磁体与钢丝绳表面之间的气隙;Lm为两永久磁铁内侧间距;hl为衔铁连接体内侧与钢丝绳表面的径向间隙;hb为衔铁连接体壁厚[20]。
笔者所画简化三维仿真模型如图5所示。

图5 简化三维仿真模型Fig.5 Simplified 3D simulation model
2.1.2 仿真分析
笔者对有损伤和无损伤的钢丝绳分别进行了有限元仿真,钢丝绳表面磁通密度分布如图6所示。

图6 钢丝绳磁通密度分布Fig.6 Magnetic flux density distribution of wire ropes
笔者设置仿真实验钢丝绳断丝损伤宽口为13 mm,外部断丝数量分别为1根、2根、3根。
在距损伤提离值5 mm处的有限元仿真结果如图7所示。
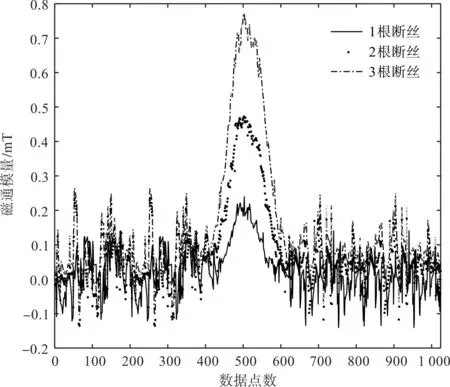
图7 3种损伤的仿真信号Fig.7 Simulation signals of three kinds of damage
图7中,曲线为钢丝绳损伤表面仿真漏磁场减去背景磁场的结果[3],可以看出:不同断丝数量的损伤漏磁强度特征有明显区分,改变模型的断口长度和断丝数量,可得到所需不同损伤程度的数据。
2.2 钢丝绳断丝实验
笔者使用6×37+FC结构的钢丝绳进行断丝试件制作,钢丝绳试件直径为24 mm,长度为5 950 mm,每隔600 mm制作一处断口宽度为13 mm~15 mm的断丝损伤。
实际制作的断丝如图8所示。

图8 钢丝绳断丝实物图Fig.8 Physical picture of broken wire ropes
该实验使用的漏磁传感器如图9所示。
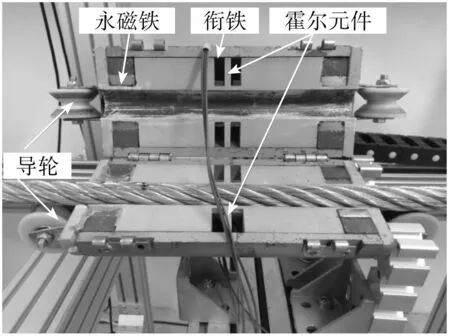
图9 漏磁传感器实物图Fig.9 Physical picture of magnetic flux leakage sensor
图9中,永磁体NdFeB35作为励磁源,与导磁衔铁构成励磁器,并与被检测钢丝绳构成磁回路,霍尔元件嵌在励磁器的中间位置[2]41。
实验使用的钢丝绳检测试验台如图10所示。

图10 钢丝绳检测试验台Fig.10 Wire rope testing test bench
笔者利用该试验台采集钢丝绳断丝损伤的原始信号,将1根断丝、2根断丝、3根断丝的信号分别从原始信号中切割出来,每处断丝的漏磁信号切割为包含1 024个数据点的数据块[21]。
切割出来的3种损伤信号如图11所示。

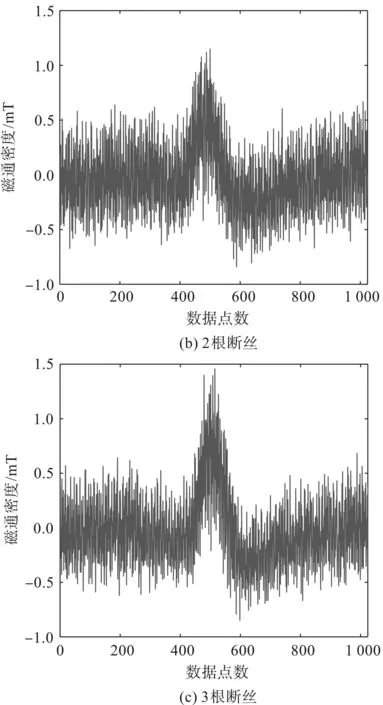
图11 3种损伤的实验原始信号Fig.11 Experimental raw signals of the three lesions
由于在漏磁检测过程中,钢丝绳产生的晃动、钢丝绳表面起伏不平,以及外界电磁干扰等,都会使采集的漏磁信号夹杂较多的噪声,导致信号失真,难以进行损伤信号的特征提取与识别,而且仿真信号中噪声干扰很小。因此,为解决实测信号中存在噪声干扰导致其与仿真信号不匹配的问题,笔者需要对实测信号进行去噪处理[22]。
由于具有良好的时频局部特性,小波变换在处理含有噪声的非平稳信号方面具有明显优势,其适合用于具有突变特性的钢丝绳断丝漏磁信号的去噪处理。
笔者采用小波变换的方式对实测信号进行去噪。小波去噪的过程实质上是先对原始信号进行小波变换,然后对得到的频带子信号进行阈值收缩处理,最后再按照小波逆变换的过程,将阈值收缩处理后的频带子信号重构为可代替原始信号的新信号。
在该实验中,笔者使用“db2”小波函数对信号进行分解去噪,结果如图12所示。
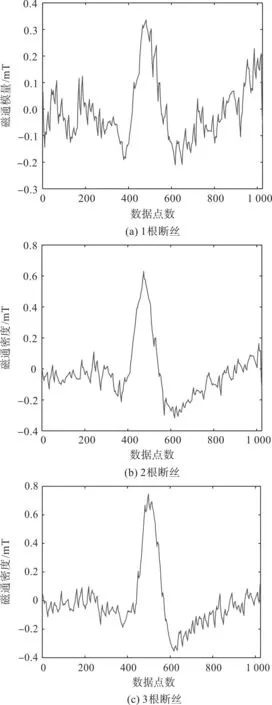
图12 小波去噪后的3种损伤实测信号Fig.12 Three kinds of damage measured signals after wavelet denoising
由图12可以看出:该小波函数对钢丝绳损伤信号具有良好的分解效果[23]。
3 基于卷积神经网络的钢丝断丝定量识别
针对工程实际中无实测样本和少量实测样本工况问题,笔者分别提出了将仿真数据作为训练集和将仿真数据辅助小样本实测数据作为训练集的方法,以提高钢丝绳断丝定量识别效果。
接下来,笔者对两种工况分别进行验证。
3.1 以仿真数据作为训练集
为证明仅以仿真数据作为训练集的有效性,在无实测样本工况下,笔者仅使用仿真数据作为模型的输入,将实测数据用于测试,并与没有训练的随机初始化参数模型及测试集中实测数据去噪前后的实验结果进行对比。
具体实验流程如图13所示(所提方法以粗体显示)。
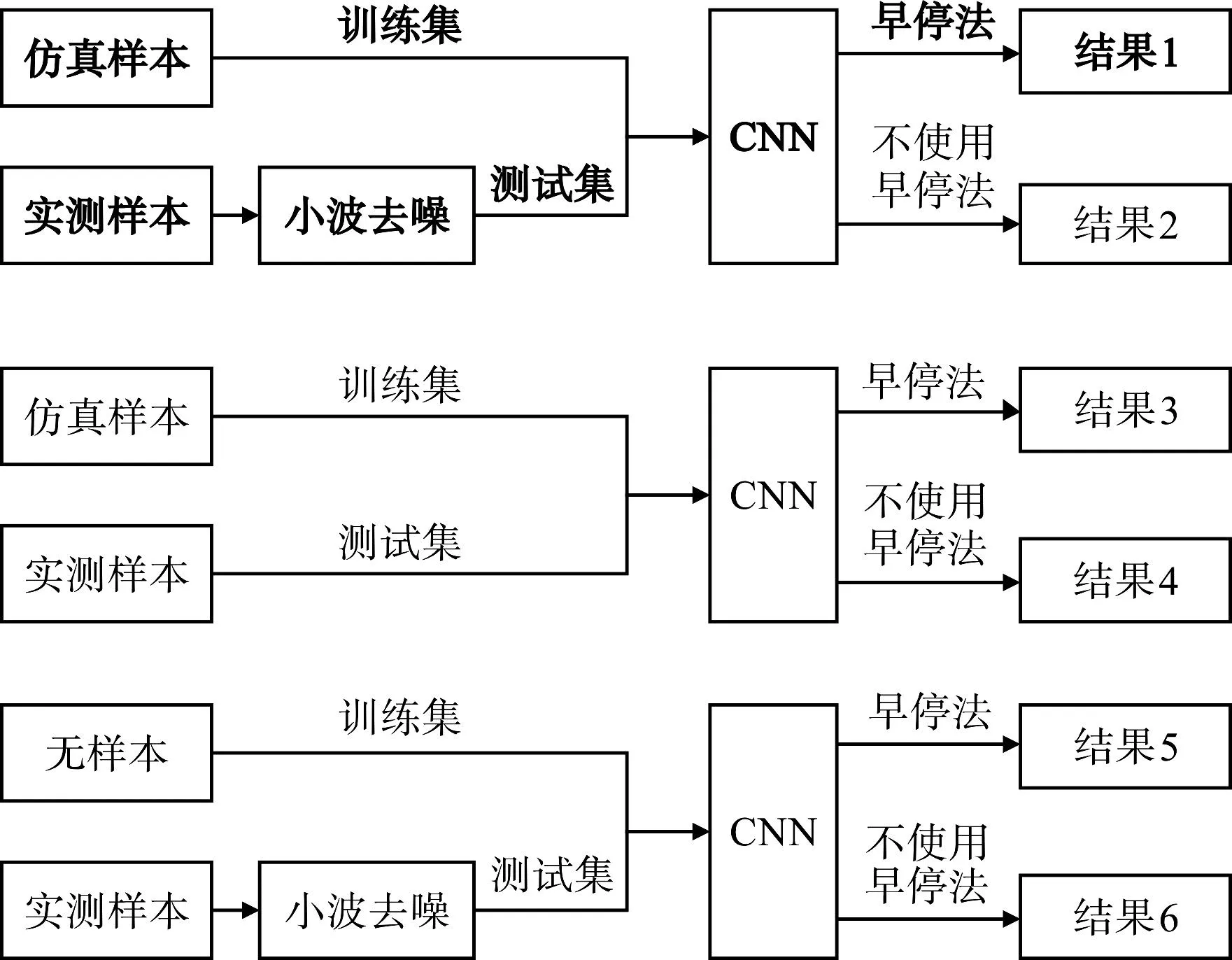
图13 无实测样本工况下实验流程Fig.13 The experimental process under the condition of no measured samples
3.1.1 数据配置
根据2.1节所介绍的仿真方法,笔者将模型断口长度分别设为13 mm、13.1 mm、13.2 mm直到15 mm,即每次增加0.1 mm;仿真的每个损伤样本为含1 024个数据点的数据块,得到共21组仿真样本。其中,每组包括1根断丝、2根断丝、3根断丝和无损伤4个样本,将21组仿真样本作为模型的训练集;测试集使用25组实测样本,其中每组包括的样本分类情况与仿真样本一致。
各类样本个数和标签如表1所示。

表1 不同故障样本个数组成及标签命名Table 1 Number composition and label naming of different fault samples
3.1.2 模型结构
在网络的训练过程中,训练环境为CPU,笔者将初始学习率设置为0.000 4,Batch-size为4。
为了增加实验的随机性,提高网络模型的泛化能力,采用shuffle-batch方法打乱样本[24-25],经过多次训练,最终得到了最优网络的各项主要参数,如表2所示。
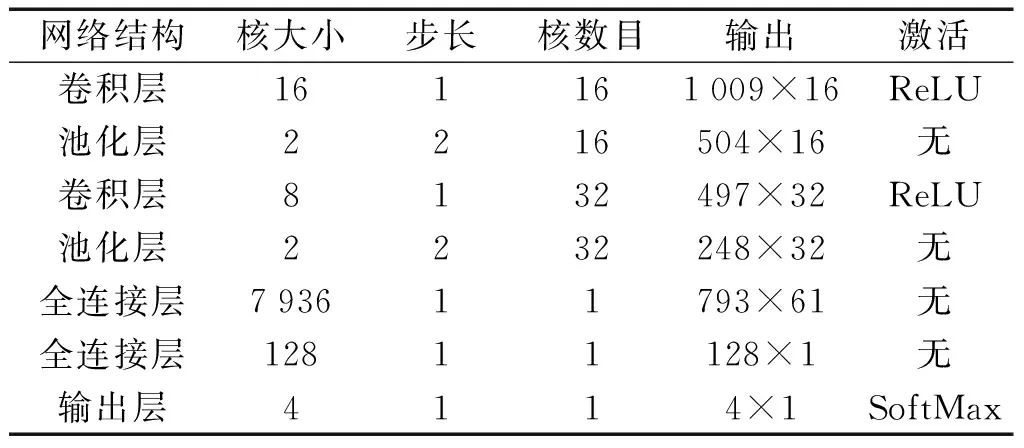
表2 卷积神经网络参数Table 2 Convolutional neural network parameters
3.1.3 结果比较与分析
笔者将模型的训练次数设置为50次,得到了训练集的损失值曲线,如图14所示。
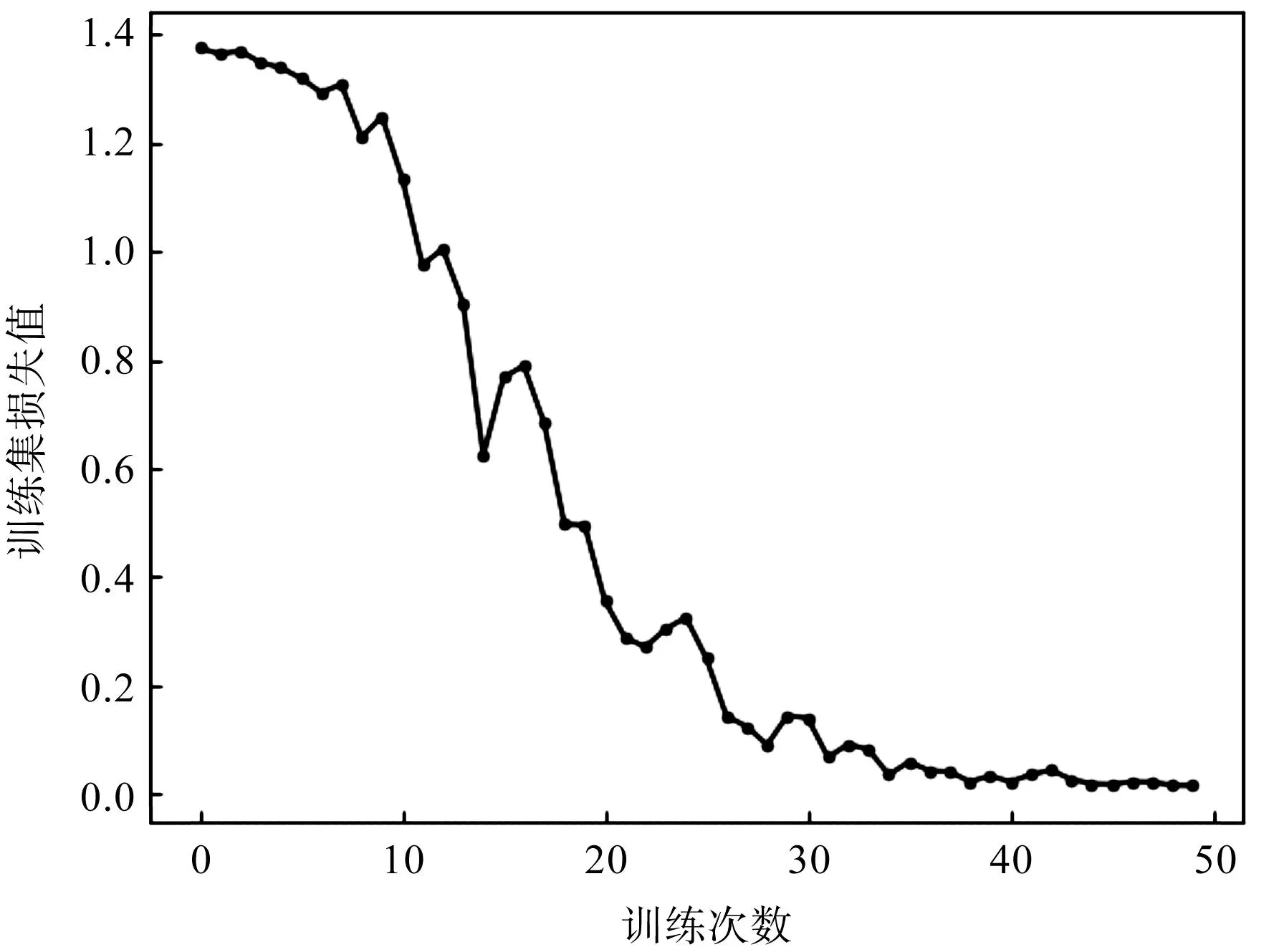
图14 训练集损失值曲线Fig.14 Training set loss value curve
从图14中可以看出:训练损失值在迭代35次之后就已收敛,此时重复实验10次得到的平均准确率为72.2%。
通过分析发现,在模型训练过程中,随着训练次数的不断增加,训练集的学习效果越来越好,错误越来越少;但当模型训练到一定程度过后,测试集的准确率会下降,此时模型就出现了过拟合。
为了使训练的模型具有更好的泛化能力,笔者使用早停法将训练次数设为22,经过10次训练取平均值得到的准确率达84.5%。在无实测样本且不使用仿真样本训练模型的情况下,准确率只有27.5%。
无实测样本工况下,训练集使用仿真样本,而测试集使用没有进行小波去噪的实测样本,进行10次实验后得到的平均准确率为53.6%,使用早停法的平均准确率为69.3%,将其结果与去噪后的结果对比,如表3所示。

表3 无实测样本工况下不同方法识别结果Table 3 Identification results of different methods under the condition of no measured samples
由表3可知:笔者使用仿真样本作为训练集,去噪后的实测样本作为测试集,并使用CNN模型进行分类,其准确率高达84.5%,高于其他方法以及分类模型,表明相对于传统的断丝识别方法,卷积神经网络大大提高了钢丝绳断丝分类准确率。
早停法能够较好地抑制仿真样本为训练集实验中的过拟合问题;仅使用仿真样本做训练集能有效辅助CNN模型训练,进而大幅度提升断丝定量识别准确率。
3.2 以仿真数据辅助小样本实测数据作为训练集
在少量实测样本工况下,因损伤数据不足导致模型训练不充分,进而严重影响断丝定量识别效果。
笔者将仿真数据辅助小样本实测数据作为训练集和只有小样本实测数据作为训练集,将其与实测数据去噪前后作对比实验,以证明将仿真数据辅助小样本实测数据作为训练集的准确率更高。
具体实验流程如图15所示。

图15 少量实测样本工况下实验流程Fig.15 The experimental process under the condition of a small number of measured samples
3.2.1 数据配置
在只有少量实测样本工况下,训练集使用20组仿真样本和5组实测样本,测试集使用25组实测样本。各类样本个数和标签如表4所示。

表4 不同故障样本个数组成及标签命名Table 4 Number composition and label naming of different fault samples
3.2.2 模型结构
在以仿真数据辅助小样本实测数据作为训练集的实验中,模型结构配置与3.1.2节相同,主要参数详见表2。
3.2.3 结果比较与分析
在少量实测样本的工况下,仅使用5组去噪后的实测样本做训练集时,由于模型训练的不充分,得到的准确率为90.2%。
为了使模型训练更充分,笔者将20组仿真样本和5组去噪后的实测样本一起作为训练集,即使用仿真样本辅助少量的实测样本进行模型训练。
由于每次训练时卷积神经网络的初始值是随机的,为了验证该实验结果的可靠性,笔者重复以上操作10次,得到平均准确率为97.5%,而使用早停法的准确率为97.4%,两者相差很小。
使用仿真样本辅助少量的实测样本进行实验时,训练集和测试集中的实测样本均采用没有进行小波去噪的数据。该实验结果取10次平均后的准确率为86.7%,使用早停法的10次平均准确率结果为86.5%。
去噪前后对比结果如表5所示。

表5 少量实测样本工况下不同方法识别结果Table 5 Identification results of different methods under the condition of a small number of measured samples
由表5可知:使用仿真数据辅助小样本实测数据作为训练集,并使用CNN模型进行断丝分类的准确率高达97.5%,表明相比于卷积神经网络,反向传播(back propagation,BP)神经网络模型以及支持向量回归(support vector regression, SVR)模型的分类准确率普遍较低。
仿真数据可以有效辅助去噪后的小样本实测数据,使CNN模型训练得更充分,进而提高钢丝绳断丝定量识别的准确率。
早停法在少量实测样本工况下的作用甚微。
4 结束语
仿真数据驱动的模式识别方法能够有效地解决故障样本不足的问题,然而目前为止尚未有相关研究成果公开发表过其在钢丝绳故障诊断领域的应用。
针对工程应用中起重机钢丝绳故障样本存在不足甚至严重缺乏的问题,笔者提出了一种仿真数据驱动的钢丝绳断丝定量识别方法,使用仿真数据辅助CNN模型训练,实现了钢丝绳断丝的定量识别目的。在无实测样本和少量实测样本两种实验形式下,验证了该方法的有效性,并得出以下结论:
1)在无实测样本工况和少量实测样本工况下,仿真数据驱动的钢丝绳断丝定量识别方法准确率分别高达84.5%和97.5%,证明了该方法能够有效地识别钢丝绳损伤,为钢丝绳损伤检测中存在的故障样本不足问题提供了新的解决思路;
2)在无实测样本和少量实测样本工况下,由于仿真数据不含有噪声等其他因素干扰,分别对比了小波变换去噪前后实测数据的结果,证明了小波去噪能够有效提高仿真数据驱动的钢丝绳断丝定量识别方法的准确率;
3)在无实测样本工况下,仅使用仿真数据作为训练集会出现过拟合问题,使用早停法提前结束训练,能使模型获得更好的泛化性能,进而提高断丝定量识别的准确率。
在断丝损伤距离较远时,该研究方法能达到很好的定量识别效果。但在实际工况应用中,当损伤距离很近时,可能会出现采集到的两处损伤信号叠加的情况。
今后,笔者将进一步丰富断丝信号数据集,补充断丝损伤在不同位置以及不同直径钢丝绳下的采集结果,以进一步提高该方法的实用性。

