随机装配侧隙均值及临界方差控制对齿轮非线性系统稳定性的影响*

曾凡灵

(安徽职业技术学院 安徽合肥 230011)

汽车变速箱故障主要表现为振动与异响，而变速箱动力传动主要以一对或多对齿轮副进行，因此齿轮副的运动形式决定了变速箱工作的稳定性。而齿轮传动过程，影响因素较大的参数是齿轮齿侧间隙(以下简称侧隙)。因此，建立含齿轮侧隙的系统模型，进而研究侧隙对齿轮非线性系统稳定性的影响[1]。

1含装配侧隙的齿轮副系统模型及动力分析

1.1含装配侧隙的齿轮副系统模型及微分方程

侧隙的度量方法：一对动力传递的齿轮副，当视其中一个固定，另一个在啮合线上的晃动量；通常可用齿轮副在啮合线上的啮合位移来表示。

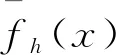
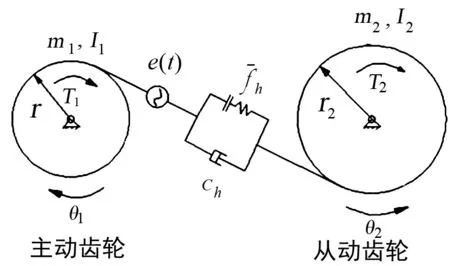
图1 含装配侧隙的齿轮副系统模型

依据图1模型，进行综合推导处理，获得无量纲化的含装配侧隙的齿轮非线性微分方程：

(1)

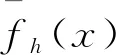
(2)

1.2侧隙对齿轮非线性系统稳定性的影响分析

研究参数变化对非线性系统稳定性影响，通常采用全局分析方法，目前最为常用的有分岔图和最大Lyapunov指数图方法。

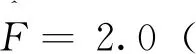
采用全局分析方法，利用Simulink软件仿真，获得系统在高速重载和高速轻载下的分叉图与最大Lyapunov指数图。由笔者前期的研究可知，可用最大Lyapunov指数衡量系统的稳定性；当最大Lyapunov指数值Ly<0，系统运动是稳定的；当Ly≥0，系统运动失稳[1]。

由图2的分岔图分析，发现随侧隙增加未出现分叉点；由最大Lyapunov指数图分析，发现随侧隙bh变化，系统的(Ly<0)均小于0。说明在高速重载下，随侧隙变化的系统响应均为周期或拟周期运动，其对系统全局运动特性影响较小[1-3]。

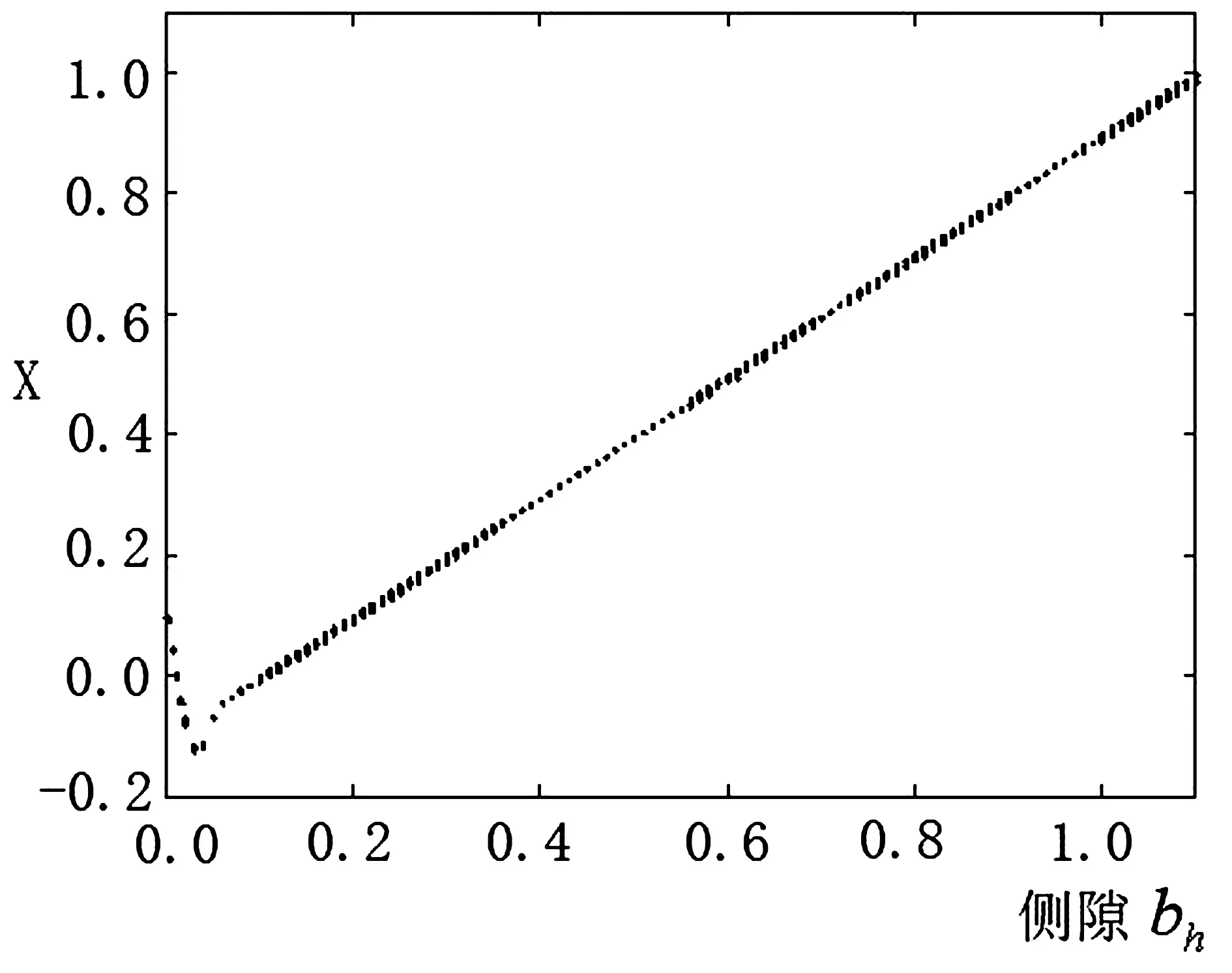
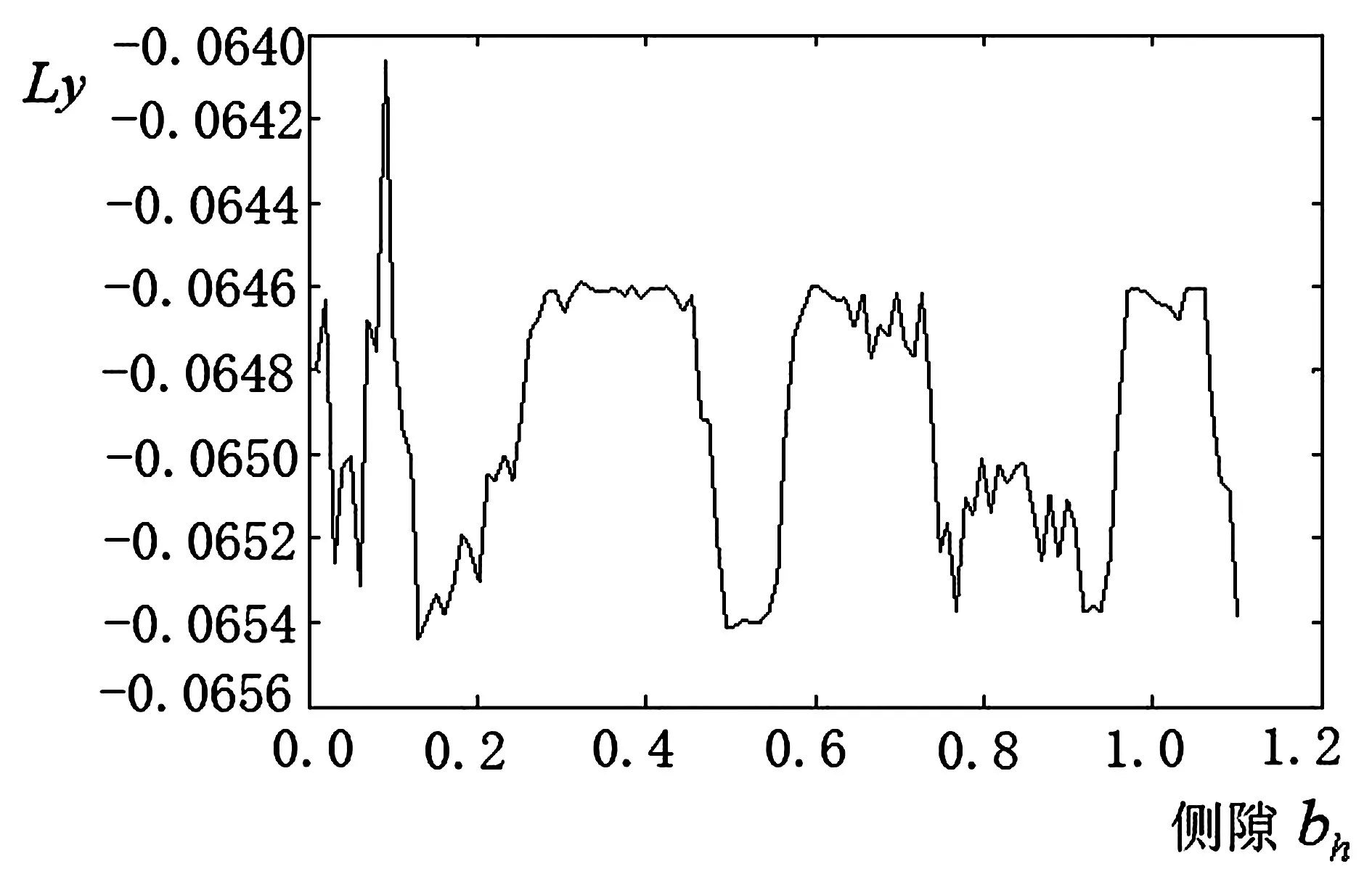
图2 高速重载下，侧隙变化的分叉图与最大 Lyapunov指数图

由图3分析发现，系统在侧隙为0.2121(①点处)，0.35485(②点处)，0.4923(③点处)，0.7280(④点处)处产生分叉现象，这些数值为侧隙的分岔点；由最大Lyapunov指数图分析，参数在0.2121～0.35485，0.4923～0.7280范围，对应的Ly≥0，说明系统在以上两区域为混沌的不稳定运动，同时局部存在Ly<0的情况，说明在混沌区域存在较窄范围的稳定周期运动；参数在其他数值范围，系统均为周期或拟周期的稳定运动。因此，在高速轻载下，侧隙的变化对系统的稳定运动特性影响较复杂，这也映证工程实际情况，高速轻载震动剧烈的问题。

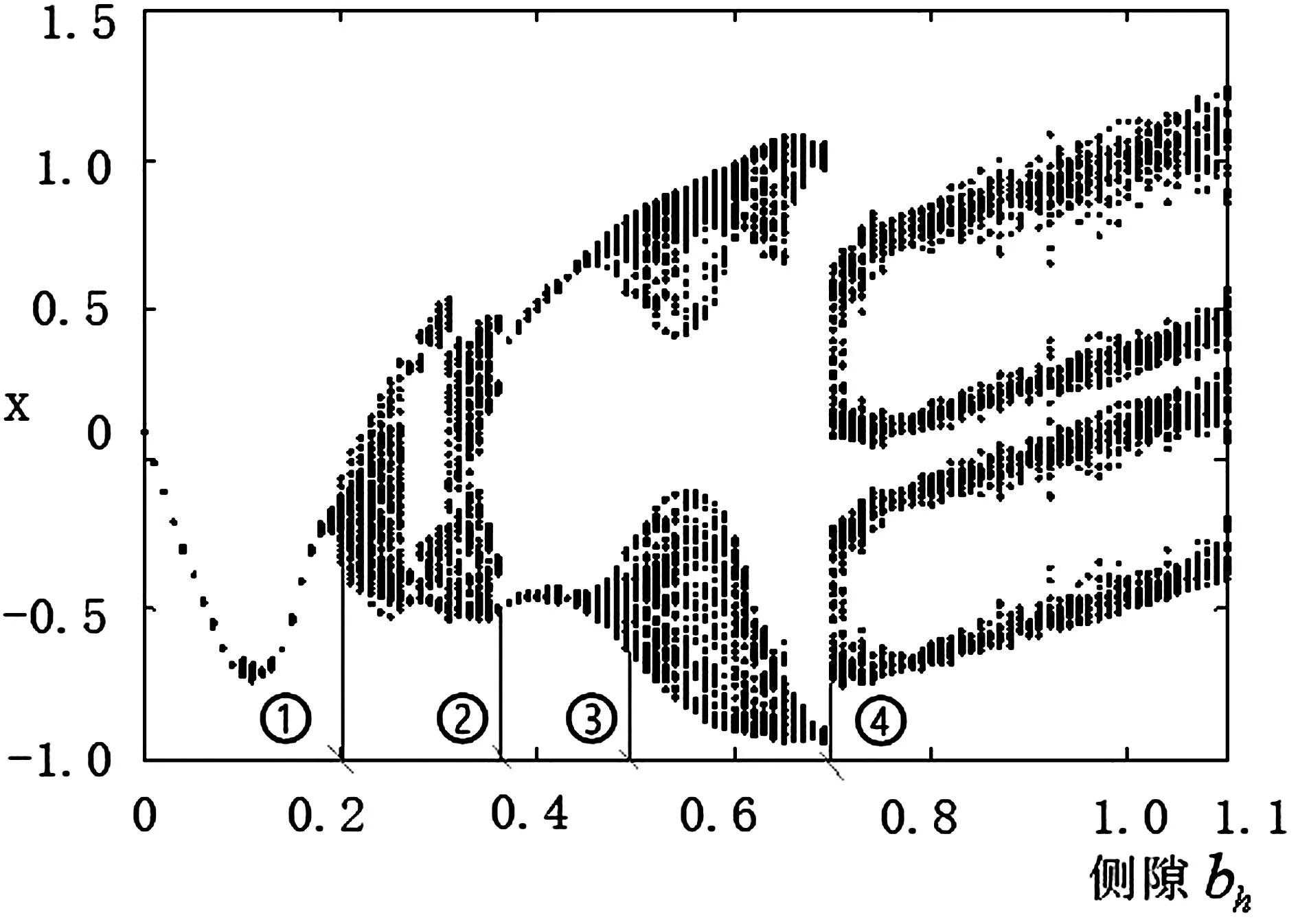
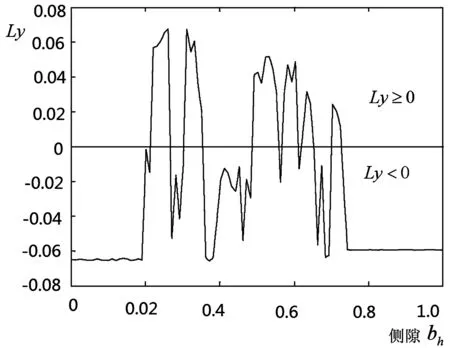
图3 高速轻载下，侧隙变化的分叉图与最大 Lyapunov指数图

2随机装配侧隙特征与随机量的产生

影响齿轮副装配侧隙大小的主要因素包括：①安装误差：齿轮副安装过程，由于齿轮中心偏移，导致齿轮副间的间隙；②制造加工误差：为了满足两齿轮装配的容差，制造加工过程允许的加工公差；③变形误差：随齿轮副的高速运动，导致轴类零件的扰屈变形以及受温度影响的材料膨胀，导致侧隙的变化。因此，装配侧隙bh由固定值bc与变动值bυ共同构成；在实际研究过程，如果考虑主要问题的影响，即bυ=0，侧隙视为固定值；如果考虑综合问题的影响，bυ≠0，因此齿轮副装配侧隙是随机的。下面重点研究随机装配侧隙特征及随机量的产生方法。

对于一批齿轮副的随机装配侧隙，bh=bc+bv，可依据中心极限定理，探究随机量的均值和方差。对bh=bc+bv进行若干次抽样，可知随机量概率分布特征近似服从正态分布，即bh～N(μ,σ2)，μ为随机装配侧隙均值，σ2为随机装配侧隙方差[1-4]。下面研究产生随机量的方法。

利用Simulink软件，在[0，1]区间上产生均匀分布伪随机数，为了产生满足均匀分布的随机量，抽样周期可足够长[1]。设ri(i=1,2,…,12)是[0，1]区间上均匀分布随机量，进行12次抽样，通过下面方法可产生满足标准正态分布随机量ξ。

(3)

随机装配侧隙服从：bh～N(μ,σ2)，则

bh=σ×ξ+μ

(4)

3随机装配侧隙对非线性系统稳定性影响

3.1失稳指数引入

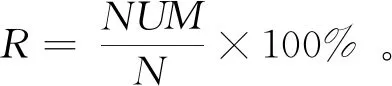
3.2高速轻载下，随机装配侧隙均值的临界方差

由于在高速重载下，无论侧隙如何变化，系统均是稳定的；而在高速轻载下，侧隙对系统稳定性影响较大。这也说明，在高速轻载下，随机装配侧隙对系统的稳定性影响较为敏感。因此，下面重点研究在高速轻载下，随机装配侧隙的均值及方差对系统稳定性的影响。由图3可知，若随机装配侧隙均值μ在0～0.2121范围，方差σ2=0.0时(即侧隙视为固定值)，系统运动特性是稳定的。下面研究固定侧隙均值，改变随机装配侧隙方差对系统稳定性的影响。

在0～0.2121范围，取均值μ=0.18，增大σ2，计算各方差对应的最大Lyapunov指数均值E(Ly)、标准偏差值STD(Ly)及失稳指数R，系统的随机量指标详见表1。同时获得各不同σ2对应的随机装配侧隙的最大Lyapunov指数图，详见图4。

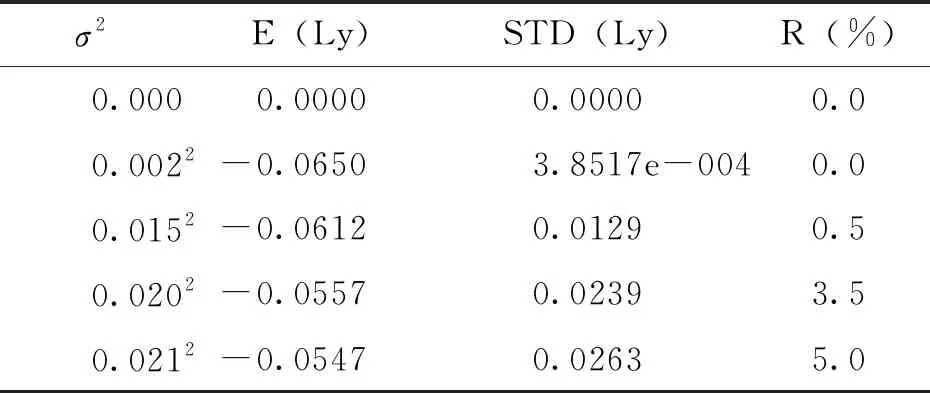
表1 均值μ=0.18时，系统的随机量指标

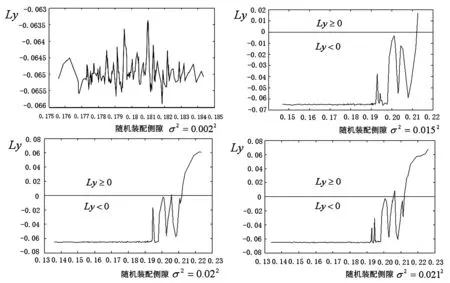
图4 μ=0.18时，不同σ2的随机装配侧隙的最大Lyapunov指数图

结合图4及表1分析，在某固定侧隙均值下，可发现随方差的增大，失稳指数是增大的；由0增加至大于0，必存在某方差使得失稳指数开始大于0的状态，此方差称为某固定侧隙均值的临界方差，用σ2表示[1]。在实际装配应用中，为了保证一批随机装配侧隙齿轮副的合格率，在选择随机装配侧隙方差时，就需要保证σ2小于σ2。

经过大量试验，发现σ2=0.0112时，R=0%；稍增加方差，即σ2>0.0112时，R均大于0%。故此，装配侧隙μ=0.18的临界方差为σ2临界=0.0112。由此，提出失稳指数和临界方差可作为随机装配侧隙对系统稳定性影响的评价指标。

3.3 系统失稳指数与临界方差关系验证

为了验证失稳指数和临界方差存在的普遍性与可行性，改变侧隙均值与方差继续进行探究。由图3知，若随机装配侧隙均值μ在0.35485～0.4923，方差σ2=0.0，系统为稳定的拟2周期运动；现取侧隙均值μ=0.37，继续研究μ、R及σ2临界的三者内部联系。增大σ2，计算各方差对应随机量的E(Ly)、STD(Ly)及R，系统的随机量指标详见表2。

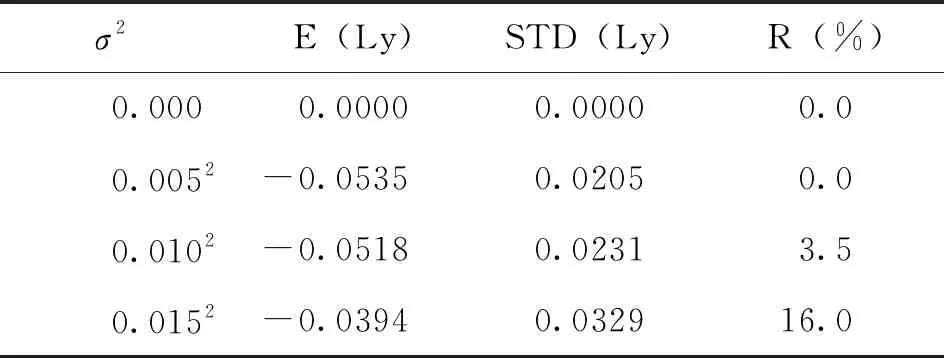
表2 均值μ=0.37时，系统的随机量指标

通过大量仿真计算，发现侧隙μ=0.37的临界方差σ2临界=0.0052。同样发现随装配侧隙的σ2、E(Ly)、STD(Ly)增大，失稳指数R也是增大的，由此验证以上结论的真实性。

4随机装配侧隙μ与σ2临界的关联分析

由上述研究结果，每一齿轮副系统，其侧隙均值都对应一临界方差。通过大量的仿真计算，可获得随机装配侧隙μ与σ2临界的一一对应关系，并绘制μ—σ2临界关系图，详见图5。

针对一批随机装配侧隙μ—σ2临界的关系图进行分析。在0～0.2121范围，随随机装配侧隙μ增大，则σ2临界减小，即越靠近0.2121(分叉点①)，σ2临界越小。结论：在齿轮副装配过程，小装配侧隙具有大的临界方差，可以降低齿轮的加工精度而提高了安装精度要求。

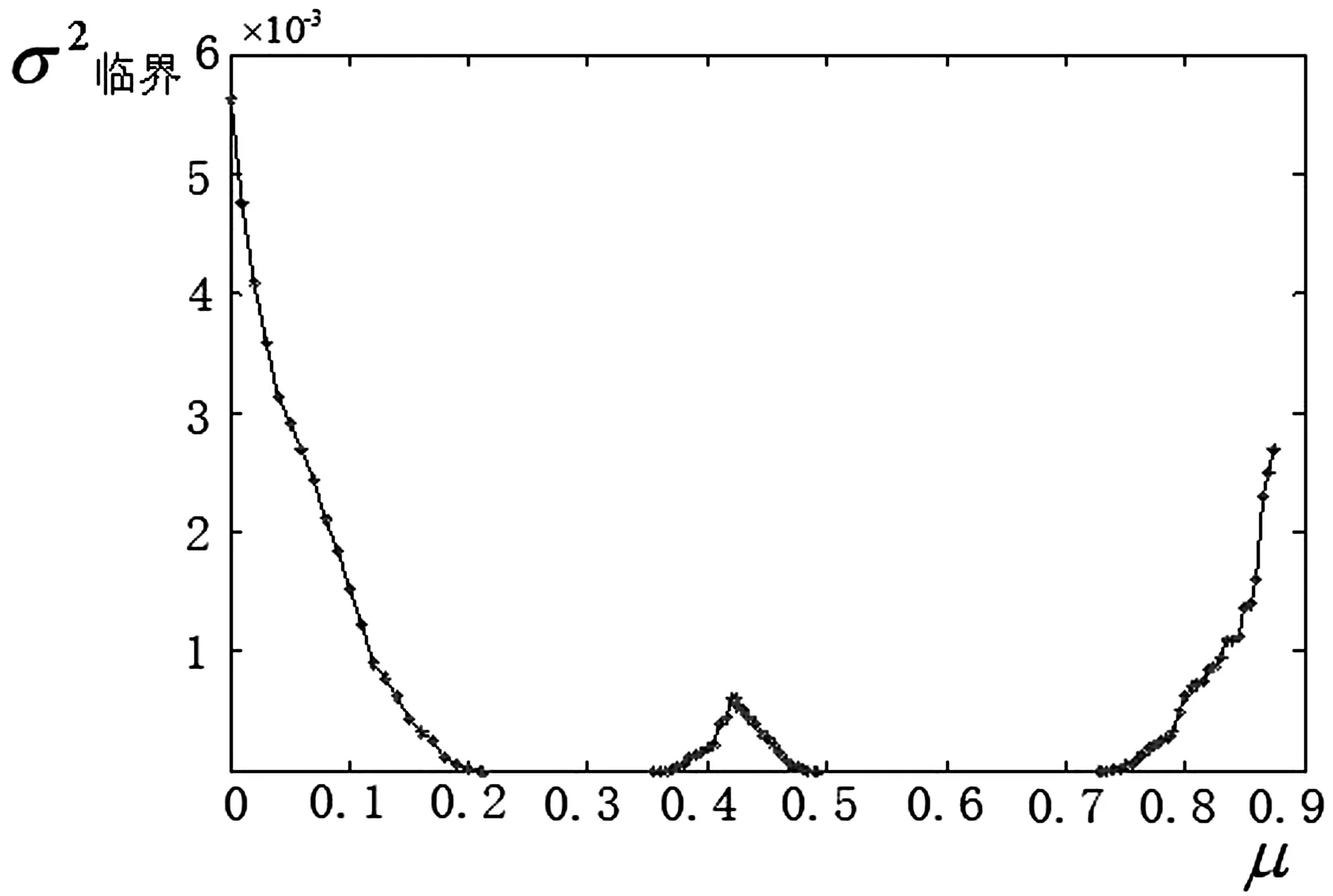
图5随机装配侧隙μ—σ2临界的关系图

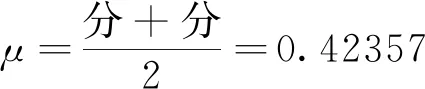
在0.7280～1.1范围，由图可见：当μ=0.7280(分叉点④)，σ2=0.0，随随机装配侧隙μ远离分岔点④，σ2临界增大。结论：在齿轮副装配过程中，选择较大装配侧隙μ，同样可以获得较大σ2临界，选择大的装配侧隙可降低齿轮副的安装精度。

5小结

随机装配侧隙均值μ及临界方差σ2临界之间具有极强的关联度，对二者进行有效联合控制，能有效提高一批随机装配侧隙齿轮系统的稳定性。在实际装配应用中，为了保证一批随机装配侧隙齿轮副的合格率，在选择随机装配侧隙方差时，就需要保证侧隙σ2小于σ2临界。