基于分子动力学的仿珍珠母长径比对力学性能影响的研究*
潘 慧 李景辉 温从众
(1安徽工业大学创新教育学院;2安徽工业大学冶金工程学院 安徽马鞍山 243000)
经过大自然不断的进化,珍珠母(Nacre)成为典型具有优异结构和力学性能的生物体系材料。珍珠母主要是由各种形状的文石片(主要成分是碳酸钙,体积分数约95%)和有机质基体以各种各样的形式堆叠而成[1-2]。但是,珍珠母的强度和硬度是其组分(文石片)的2倍,断裂能达到其成分碳酸钙的3000余倍[3]。层级结构是珍珠母具有如此优异的力学性能的主要原因,研究表明,特别是微纳米级尺度层级结构为材料的力学性能起到至关重要作用[4-6]。为此,许多学者围绕珍珠母结构的韧性增强机制进行了研究。Song等人发现矿物桥不仅可以增加断裂强度还能帮助裂纹实现偏转[7],Katti等人通过有限元模拟发现韧性增加的另一因素是文石片的“自锁”结构[8];Gao等人珍珠母结构中,大部分载荷由文石片承担,生物有机质起着传递载荷的作用,并由此提出一种“拉伸-剪切链(TSC)模型”[9];Francois Bathelat提出了一种裂纹桥连和过程区微观力学的韧性模型,揭示微结构参数控制珍珠母的整体韧性[10-11];Sina Askarinejad用实验和有限元模拟的方法研究了珍珠母tablet波纹度对整体韧性的影响[12]。自然界的生物材料同时拥有强度,硬度和韧性于一体,生物材料的这些闪光点使得科学家们对其不断的实验研究,并模拟其变形过程,为新合成材料的开发奠定理论基础[13]。仿生材料还需向工程材料转移,目前有学者研究了仿生金属基纳米复合材料的力学性能,但是仿生陶瓷基金属复合材料力学性能及失效机制的研究很少。文章主要研究陶瓷基仿生纳米复合材料的微结构参数对其材料整体力学性能及失效机制的影响,为开发纳米复合材料提供了理论指导和依据。
文章结合理论模型应用分子动力学模拟的方法,揭示了“砖-泥”微结构中增强体长径比对仿陶瓷基体金属复合材料力学性能的影响。结果表明,仿珍珠母复合材料的长径比对材料的杨氏模量和韧性都有影响,并存在一个长径比临界值,此临界值诱发复合材料不同的失效机制。当仿珍珠母复合材料增强体长径比小于临界值时,其失效模式是孔洞沿增强体端部的两侧聚集成45度裂纹,呈现“增强体拔出行为”,然而当长径比大于临界值时,裂纹纵向贯穿增强体,呈现“增强体的断裂行为”。
1理论模型与计算方法
1.1理论模型
Francois Barthelat等人提出微结构参数如何控制韧性的理论模型[10-11]。模型分析了裂纹桥接和裂纹过程区如何稳定状态下复合材料总韧性的贡献。Jackson提出片层拔出是主要的脱粘机制,这种拔出被认为是裂纹桥接,是一种外在的增韧作用。拔出机制产生长度为λ的内聚区域,假设界面剪应力为τs,界面韧性为:
(1)
umax是界面内聚力消失的滑移距离,τs的真实值为20-25MPa,桥接力之间的距离为2t。为突出韧性与微结构之间的关系,韧性的表达式也可以写为:
(2)
该公式揭示了微观结构参数对韧性的影响。文章主要研究微结构中长径比L/t对力学性能及失效机制的影响。
1.2分子动力学模拟方法
文章应用分子动力学的方法,建立复合材料的粗粒化模型,如图1所示所示。模拟软件采用LAMMPS软件(large-scale atomic molecular massively parallel simulator)[14],模拟对象为120000个原子,有2种原子类型。拉伸方向选用自由边界条件,其他方向为周期性边界条件。时间步长为0.0001。势函数选用Lennard-Jones(LJ)势,LJ势提供原子间相互作用一般特征的基本描述,广泛用于研究力学行为以及材料的断裂失效等行为[15-16]。
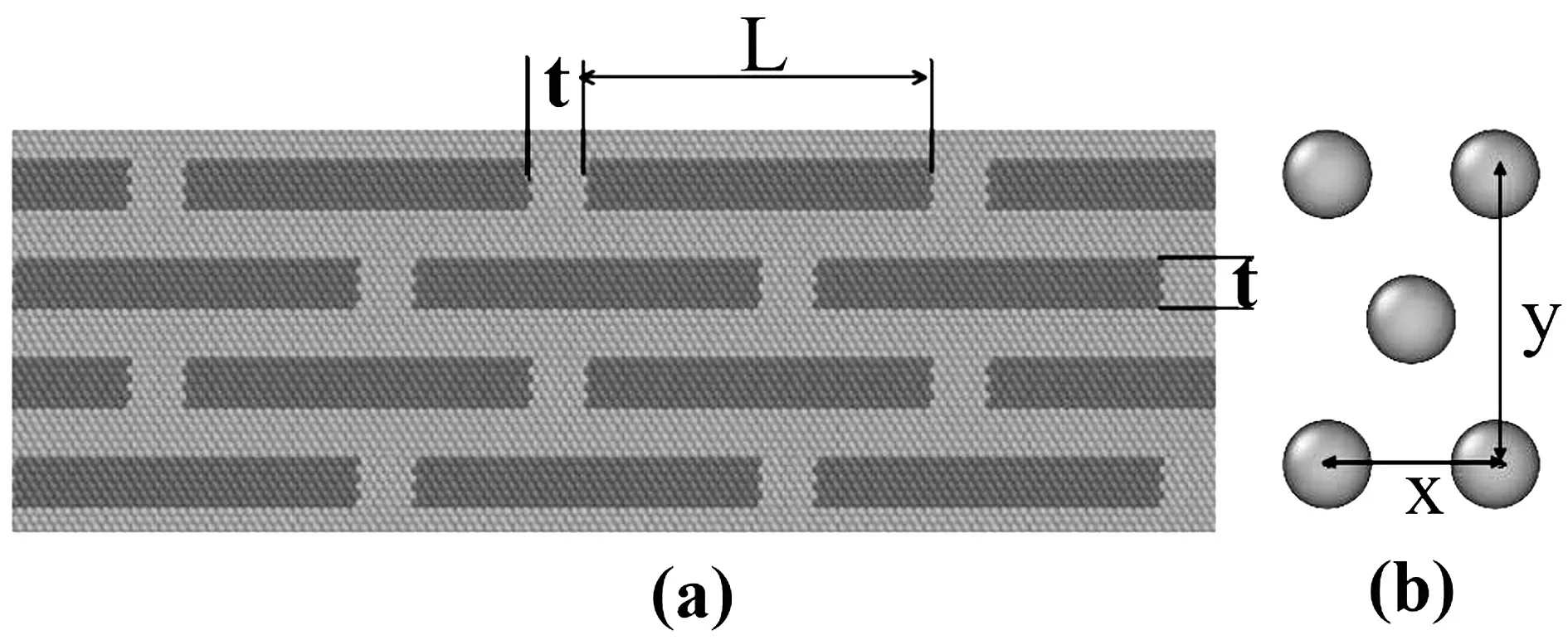
(a)交错“砖泥”结构的复合材料分子模型 (b)hexagonal晶格结构的基本单元图1 分子模拟模型的建立
文章中,LJ势和六边形晶格结构相结合可捕捉材料的一般脆性行为[17-18]。尽管复合材料的粗粒化二维模型是真实系统的简化,却能揭示一般力学行为。LJ势如式所示,LJ势是无量纲单位。
仿珍珠母复合材料由硬、脆的矿物质相(增强体)和软、易延展的蛋白质相(基体)组成。LJ势参数ε控制这两个成分的刚度和强度,参数σ控制晶格参数。为保证构件的稳定平衡结构,两种组分的参数σ保持一致。文章中,设定矿物质相和蛋白质相的LJ参数σ为1,矿物质相参数ε为1,而蛋白质相的LJ参数ε为0.1。文章模拟中,所有单位无量纲化。
对图沿x方向进行单轴拉伸,在模型的底层速度设为0,顶层施加恒定应变率为0.00001,为避免内部原子与边界原子的速度不同而引起震动,从底层到顶层设置一个线性梯度。用采用Berendsen控温和控压方法,温度设定为0.0001(无量纲单位),垂直于拉伸方向压力为0。在对模型进行拉伸之前,在温度为0.0001(无量纲单位)对系统进行驰豫,以获得应力自由的初始结构。使用可视化软件OVITO[19]处理分子模拟的数据。文章中,保证矿物质相的重叠为1/2,改变矿物质相的长度(宽度保持不变),研究长径比对力学性能的影响。
2模拟结果与讨论
2.1增强体长径比对整体力学性能的影响
为探索不同长径比模型对材料整体力学性能的影响,设计了长径比AR=12;AR=26;AR=36;AR=46的模型以及均匀材料模型,并对它们的应力应变曲线进行了研究。从图2中可以看出,含增强相结构材料的应力应变曲线,其强度极限明显高于均匀体材料的强度极限。对于均匀体材料模型,当其达到强度极限时,应力突然下降为0,属于脆性断裂,其原因是文章设计的基体相材料就是脆性材料。对于具有砖泥结构的材料,当其达到强度极限时,应力不是瞬时降为0 ,而是有一个下降的过程,说明“砖泥”结构让模型材料的脆性断裂行为有所改善。
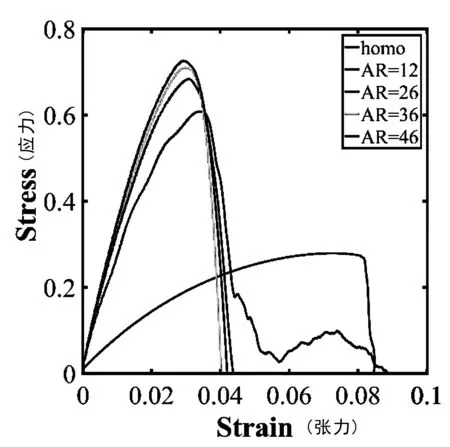
图2 增强体不同长径比复合材料的应力应变曲线
从图2可以看出,随着模型材料长径比的增加,其极限应力也相应增大,当AR=46时,其强度极限接近均匀体材料模型强度极限的3倍。
2.2增强体长径比对杨氏模量的影响
为探索增强相长径比对材料整体杨氏模量的影响,研究了均匀体(AR=0)及其他不同长径比(AR=6,8,10.36)与材料杨氏模量的关系。如图3所示,随着长径比的增加,杨氏模量刚开始呈上升趋势,但随着长径比的逐渐增加,杨氏模量缓慢增加并呈稳定值。随着长径比增加,材料抵抗变形能力逐渐增强,当长径比增加到一定值时,材料抵抗变形的能力趋于不变。这反应了材料的刚度的变化趋势,即刚开始随长径比增加刚度增加,而后趋于稳定。

图3 复合材料增强体长径比与杨氏模量的关系
2.3增强体长径比对韧性的影响
文章讨论了不同长径比对材料整体韧性的影响。从图4中可以看出,对于砖泥结构而言,随着长径比的增加,材料的韧性呈线性增加的趋势,但达到一定值以后,长径比继续增加,而其韧性值呈下降趋势。此长径比AR=18称其为“韧性值临界AR”。韧性是材料性能的一个关键参数,韧性的增加可让材料获得更好的力学性能。韧性的增加可减少材料发生脆性断裂的几率,脆性断裂是发生安全事故的主要原因之一。获得韧性和刚度的结合是设计新材料的重要目标。

图4 复合材料增强体长径比与韧性的关系
2.4失效机制
为探寻仿珍珠母复合材料的失效机制,对模型的原子轨迹进行了可视化的分析。以“韧性值临界AR”为分界分别研究了AR=12和AR=26两种模型原子运动轨迹。对于长径比AR=12的模型,其几何结构随应变率变化的过程如图5所示。其失效过程可分为三个步骤:①增强体的端部出现孔洞;②孔洞沿增强体端部的两侧聚集成45度裂纹;③增强体在端部裂纹的作用下从基体中脱离,呈现增强体的拔出行为。这个机制称之为“增强体拔出行为”。对应于图2的应力应变行为可以发现,应力下降以后有缓慢上升现象出现,孔洞以及裂纹的出现使得应力出现下降行为。但是裂纹聚集以后并没有立即使得材料发生断裂,而是呈现“增强体拔出”行为,这使得应力又出现了小幅度回升现象。

图5 长径比AR=12时仿珍珠母复合材料的变形机制
对于大于“韧性值临界AR”的模型,选择AR=26的模型来研究其失效过程。其可以分为三个阶段:首先相邻两增强体的中间部位聚集成±45度裂纹;然后裂纹开始纵向扩展,并触及相邻上下增强体的表面;最后裂纹纵向贯穿增强体,呈现“增强体的断裂行为”。对应于应力应变曲线,裂纹的出现使得应力出现下降现象,随后发生的裂纹贯穿增强体,增强体被完全破坏,对应其应力应变图可以发现,应力瞬速下降并为0。见图6。
“增强体的断裂行为”与“增强体拔出”是仿珍珠母材料两种不同的失效机制,“增强体的断裂行为”是材料的脆性断裂行为的内在原因,“增强体拔出”可为仿珍珠母塑性增强提供一些理论支撑。

图6 长径比AR=26时仿珍珠母复合材料的变形机制
3结论
文章研究了仿生纳米复合材料结构与力学行为的关系。探寻了仿珍珠母复合材料结构中增强体“长径比”对其力学性能的影响,提出临界长径比诱发不同的失效机制。
(1)通过模拟研究发现,对于均匀体材料模型,当其达到强度极限时,应力突然下降为0,属于脆性断裂;对于具有砖泥结构的材料,当其达到强度极限时,应力不是瞬时降为0,而是有一个下降的过程,说明“砖泥”结构让模型材料的脆性断裂行为有所改善。
(2)长径比存在“韧性值临界AR”,长径比临界值诱发材料不同的失效机制;当增强体长径比大于临界长径比时,其失效机制是“增强体的断裂行为”;当小于临界长径比时,其失效机制是“增强体拔出行为”。

