Klein-Gordon-Schr?dinger方程的几种差分格式及比较

林周瑾 汪佳玲 霍昱安

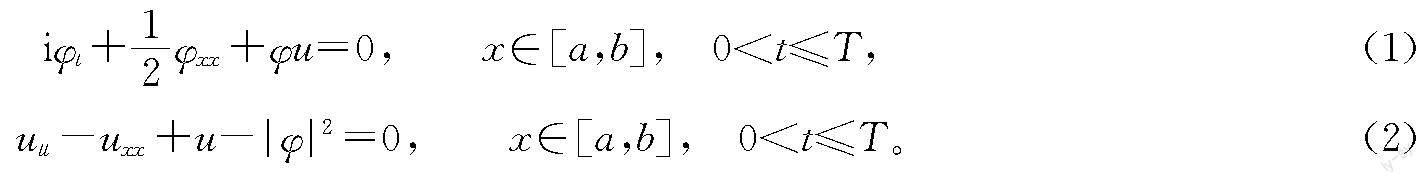
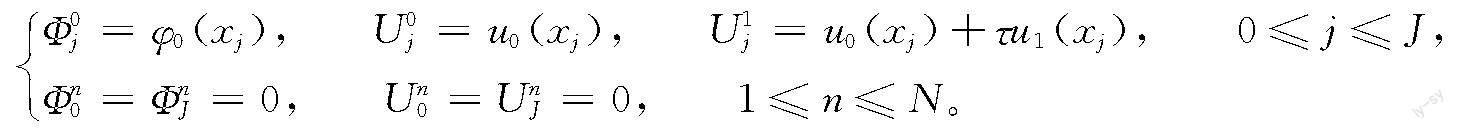
摘要： 探究在特定的初值和边界条件下一维Klein-Gordon-Schr?dinger方程的几种差分格式并进行比较。利用经典的向前差分算子、中心差分算子、Crank-Nicolson方法和紧差分算子分别为Klein-Gordon-Schr?dinger方程构造向前Euler式、Crank-Nicolson格式及紧差分格式。结果表明：Crank-Nicolson格式及紧差分格式能够精确地保持离散电荷和能量守恒。数值实验验证了理论结果的正确性。

关键词：Klein-Gordon-Schr?dinger方程； 向前Euler格式； Crank-Nicolson格式； 紧差分格式； 电荷守恒； 能量守恒

中图分类号： O 241.82文献标志码： A   文章编号： 1000-5013（2024）01-0108-13

Several Difference Schemes and Comparisons for  Klein-Gordon-Schr?dinger Equation

LIN Zhoujin， WANG Jialing， HUO Yu′an

（School of Mathematics and Statistics， Nanjing University of Information Science and Technology， Nanjing 210044， China）

Abstract： Several difference schemes of one-dimensional Klein-Gordon-Schr?dinger equation under specific initial value and boundary conditions are investigated and contrasted. The classical forward difference operator， central difference operator， Crank-Nicolson method and compact difference operator are used to construct forward Euler scheme， Crank-Nicolson scheme and compact difference scheme respectively. Results show that Crank-Nicolson scheme and the compact difference scheme can accurately conserve the discrete charge and energy conservation. The correctness of the theoretical result has been verified by numerical experiments.

Keywords： Klein-Gordon-Schr?dinger equation； forward Euler scheme； Crank-Nicolson scheme； compact difference scheme； charge conservation； energy conservation

Klein-Gordon-Schr?dinger（KGS）方程是薛定諤方程的狭义相对论形式，该系统于1970年被Yukawa首次提出。1975年，由Fukuda和Tsutsumi提出了带有Yukawa作用的KGS系统模型［1］，被用来描述量子场理论中守恒复标量核子场与实标量介子场之间相互作用，是相对论量子力学和量子场论中的最基本方程。随着学术科研的发展与科学技术的创新，KGS方程的研究越来越受到国内外学者的重视。在过去的二十年中，许多学者们针对KGS方程的解析解和数值解进行了一系列的研究。

在数学方面，Fukuda等［1］讨论了三维空间中耦合的KGS方程的初边值问题，建立了初边值问题整体解的存在唯一性定理。Baillon等［2］讨论了耦合的KGS方程的柯西问题，并且证明了KGS方程柯西问题的唯一整体解的存在性。Darwish等［3］设计了一种代数方法来统一构造KGS耦合方程的一系列显式精确解。Wang等［4］用雅可比椭圆函数展开法的推广得到KGS方程的周期波解。文献［5-10］也在数学上对KGS方程展开研究。

然而，该方程的解析解很难得到，大多数情形只能靠数值方法进行求解。因此，对于如何得到能够长时间地保持系统解的行为的KGS方程的数值解就显得尤为重要。在数值方面，学者们利用许多不同的数值方法对KGS方程进行了数值计算［11-17］。Wang［11］提出一个紧差分格式来计算具有齐次Dirichlet边界条件的KGS方程。通过连接合适的辛Runge-Kutta-type方法和辛Runge-Kutta-Nystr?m-type方法，Hong等［12］提出了KGS方程的显式多辛格式，并证明用该方法构造的方法是多辛的，可在适当的边界条件下精确地保持离散电荷守恒定律。Wang等［13］提出用傅里叶谱方法求解具有周期边界条件的空间分数阶KGS方程，并且表明该格式可以保持离散电荷和能量守恒。

基于此，本文在一定的初值和边值条件下，利用不同的差分格式求解一维KGS方程并进行比较。

1 数值格式的构造

在区域Ω=［a，b］×［0，T］上考虑一维KGS方程，即

选取初值条件

φ（x，0）=φ0（x），  u（x，0）=u0（x），  ut（x，0）=u1（x），  x∈［a，b］（3）

和Dirichlet零边界条件

φ（a，t）=φ（b，t）=0，  u（a，t）=u（b，t）=0，  t∈（0，T］。（4）

式（3）中：φ0（x）是给定的具有足够光滑性的复值函数；u0（x）和u1（x）是两个给定的具有足够光滑性的实值函数，这3个函数充当求解过程中的初始解。

式（1）～（4）具有电荷守恒律和能量守恒律，即

定义空间

V0h={v|v={vj|0≤j≤J}∈Vh，v0=vJ=0}

和三对角矩阵

其中：矩阵A根据二阶中心差分算子可得，矩阵B为对角占优矩阵，因此是可逆矩阵。

设u，v∈Vh，定义离散内积和离散范数，即

2 几种差分格式

2.1 向前Euler格式

令Φnj=φ（xj，tn），Unj=u（xj，tn）。在节点（xj，tn）处考虑KGS方程（1）～（2），有

式（7），（8）中：0≤n≤N-1；1≤j≤J-1。

由向前差分算子及二阶中心差分算子，有

将式（9）～（12）代入式（7），（8），得到

结合式（3），（4），可得

忽略式（13），（14）的小量项，则有

并用φnj，unj分别代替Φnj，Unj，得到差分格式为

式（15）～（18）即为KGS方程的向前Euler格式。称R（1）j，n和R（2）j，n为差分格式（15）和差分格式（16）的局部截断误差。记

则可知截断误差R（1）j，n，R（2）j，n满足

|R（1）j，n|≤c1（τ+h2），  0≤n≤N-1， 1≤j≤J-1，|R（2）j，n|≤c2（τ2+h2），  1≤n≤N-1， 1≤j≤J-1。

其中：c1，c2是与h和τ无关的常数。

注1 向前Euler格式（15）～（18）是一个非线性显性格式，并且该格式下φ的数值解在时间方向和空间方向上分别具有1阶和2阶精度，u的数值解在时间方向和空间方向上都具有2阶精度。

2.2 Crank-Nicolson格式

其中：0≤n≤N-1；1≤j≤J-1。

应用公式

可得到

再利用式（9）及

可以得到

在（xj，tn+1/2）处考虑方程（2），即

式（24）中：1≤n≤N-1；1≤j≤J-1。

结合式（11），（12），（21）及

可将式（24）改写为

略去式（23）和式（28）的小量项，则有

结合初值条件（3）和邊值条件（4），并用φnj，unj分别代替Φnj，Unj，得到Crank-Nicolson差分格式为

式（29）～（32）即为KGS方程的Crank-Nicolson格式。称R（3）j，n和R（4）j，n为差分格式（23）和差分格式（28）的局部截断误差。记

则可知截断误差R（3）j，n，R（4）j，n满足

|R（3）j，n|≤c3（τ2+h2），  0≤n≤N-1， 1≤j≤J-1，|R（4）j，n|≤c4（τ2+h2），  1≤n≤N-1， 1≤j≤J-1。

其中：c3，c4是与h和τ无关的常数。

注2 与向前Euler格式不同，Crank-Nicolson格式（29）～（32）是一个非线性隐性格式，并且该格式下φ和u的数值解在时间方向和空间方向上都具有2阶精度。

2.3 紧差分格式

在点（xj，tn+1/2）处考虑方程（1），有

其中：0≤n≤N-1；1≤j≤J-1。

结合式（19）～（22），有

式（33）中：0≤n≤N-1；1≤j≤J-1。

式（33）两边同时左乘紧差分算子Ah，可以得到

由于有

所以有

将式（35）代入式（34），有

在点（xj，tn+1/2）处考虑方程（2），有

式（37）中：1≤n≤N-1；1≤j≤J-1。

将式（25）～（27）代入式（37），可以得到

将式（38）两边同时左乘紧差分算子Ah，并利用式（11）及

可得

略去式（36）和式（39）中的小量项，则有

结合初值条件（3）和边值条件（4），并且用φnj，unj分别代替Φnj，Unj，得到KGS方程的紧差分格式为

式（40）～（43）即为KGS方程的紧差分格式。称R（5）j，n和R（6）j，n为差分格式（36）和差分格式（39）的局部截断误差。记

则可知截断误差R（5）j，n，R（6）j，n分别满足

|R（5）j，n|≤c5（τ2+h4），  0≤n≤N-1， 1≤j≤J-1，

|R（6）j，n|≤c6（τ2+h4），  1≤n≤N-1， 1≤j≤J-1。

其中：c5，c6是与h和τ无关的常数。

注3 紧差分格式（40）～（43）也是一个非线性隐性格式，并且该格式下的φ和u的数值解在时间方向和空间方向上分别具有2阶和4阶精度。

3 守恒性

引理1［18］ 对于任意的u，v∈V0h，有〈δ2xu，v〉=-〈δ+xu，δ+xv〉。

引理2［18］ 对于任意的u∈Vh，n=0，1，…，N-1，则有

Re〈-B-1A（un+1+un），（un+1-un）〉=|||δxun+1|||2-|||δxun|||2，

Im〈B-1A（un+1+un），（un+1-un）〉=0。

其中：Re和Im分别表示取函数的实部和虚部。

定理1 Crank-Nicolson格式（29）～（32）能够精确地保持离散的电荷和能量守恒，即

Qn=φn2≡Q0，  n=1，2，…，N，（44）

En=un2+δ+tun2+δ+xun2+δ+xφn2-2〈un，|φn|2〉=E0，  n=1，2，…，N-1。（45）

证明：式（29），（30）可以表示为

将式（46）与φn+1/2作内积，并取虚部，有

由引理1可知

〈δ2xφn+1/2，φn+1/2〉=-〈δ+xφn+1/2，δ+xφn+1/2〉=-δ+xφn+1/22∈R。

又

因此，有

故有

φn+12=φn2。（48）

因此，式（44）成立。

将式（46）与φn+1-φn做内积，并取实部，有

对上式进行逐项分析，即

整理可以得到

-δ+xφn+12+δ+xφn2+〈un+1+un，|φn+1|2〉-〈un+1+un，|φn|2〉=0。（49）

将式（47）与un+1-un做内积，有

〈δ2tun+1/2，un+1-un-1〉-〈δ2xun+1/2，un+1-un〉+〈un+1/2，un+1-un〉-12〈|φn|2+|φn+1|2，un+1-un〉=0。

对上式进行逐项分析，可得到

整理得到

δ+tun+12-δ+tun2+δ+xun+12-δ+xun2+un+12-un2-〈|φn|2+|φn+1|2，un+1-un〉=0。（50）

用式（50）減去式（49）得到

un+12+δ+tun+12+δ+xun+12+δ+xφn+12-2〈un+1，|φn+1|2〉=un2+δ+tun2+δ+xun2+δ+xφn2-2〈un，|φn|2〉，

因此，式（45）成立。

定理2 紧差分格式（40）～（43）能够精确保持离散电荷和能量守恒，即

Qn=φn2≡Q0，  n=0，1，…，N，（51）

En=un2+δ+tun2+|||δxun|||2+|||δxφn|||2-2〈un，|φn|2〉≡E0，  n=0，1，…，N-1。（52）

证明：利用前面定义的矩阵A和B，式（40），（41）可以表示为

将式（53）与φn+1/2作内积，并取虚部，则有

对上式进行逐项分析，有

又〈un+1/2φn+1/2，φn+1/2〉∈R，所以有

由此可知，式（51）成立。

将式（53）与δ+tφn作内积，并取实部，有

逐项分析，有

则式（56）可表示为

|||δxφn+1|||2-|||δxφn|||2-〈un+1+un，|φn+1|2〉+〈un+1+un，|φn|2〉=0。（57）

将式（54）与δ+tun作内积，并取实部，有

分析式（58）的每一项，可得

则式（58）可以写成

δ+tun+12-δ+tun2+|||δxun+1|||2-|||δxun|||2+un+12-un2-〈|φn|2+|φn+1|2，un+1-un〉=0。（59）

结合式（57）与式（59），有

un+12+δ+tun+12+|||δxun+1|||2+|||δxφn+1|||2-2〈un+1，|φn+1|2〉=un2+δ+tun2+|||δxun|||2+|||δxφn|||2-2〈un，|φn|2〉。

由此可知，式（52）成立。

4 数值实验

通过数值实验验证前面的理论结果。根据文献［19］可以得到KGS方程的解析解，即

式（60），（61）中：v为孤立波的传播速度；x0为初始相位。对于固定的t，当x→∞时，φ（x，t）和u（x，t）迅速衰减到0。因此，在数值上可以在有限区域（a，b）中求解KGS方程。其中，-a，b1，边界条件为零边界。

4.1 数值解

考虑初值条件

φ0（x）=φ（x，0，v，0），  u0（x）=u（x，0，v，0），  u1（x）=ut（x，0，v，0）。

计算主要在区间［-20，20］中进行，选取空间步长h为0.2，时间步长τ为0.001 s，传播速度v为0.1。向前Euler格式、Crank-Nicolson格式和紧差分格式在数值运算时间（T）分别为1，16 s时得到的数值解，如图1～3所示。

由图1～3可知：当T=16时，向前Euler格式的数值解出现了一些轻微的振荡，Crank-Nicolson格式和紧差分格式的数值解较为光滑。这表明相较于其他两种稳定的隐式格式，作为显式格式的向前Euler格式相对不稳定。

当T分别为1，16 s时，分别运用向前Euler格式、Crank-Nicolson格式和紧差分格式求解KGS方程时的CPU运行时间（tCPU），结果如表1所示。由表1可知：显式的向前Euler格式的计算速度明显优于隐式的Crank-Nicolson格式和紧差分格式，这是因为向前Euler格式在计算过程中没有迭代。

4.2 電荷守恒与能量守恒

分别定义离散电荷误差error Q和能量误差error E为

式（62）中：Qn和En分别表示第n步的电荷值和能量值。计算在区间［-20，20］中进行，选取空间步长h为0.2，时间步长τ为0.001 s，传播速度v为0.1。分别绘制T=10 s时Crank-Nicolson格式和紧差分格式的电荷、能量值及其离散误差，如图4，5所示。

由图4可知：电荷误差和能量误差分别在10-13和10-12左右，表明Crank-Nicolson格式的电荷和能量是守恒的。由图5可知：紧差分格式的守恒量误差分别在10-11和10-12左右，表明紧差分格式能够很好地保持离散电荷和能量守恒。

5 结束语

利用经典的差分算子为一维KGS方程分别构造向前Euler格式、Crank-Nicolson格式和紧差分格式。利用相关理论知识讨论了3种格式的精度，详细证明了Crank-Nicolson格式和紧差分格式能够精确保持离散电荷守恒及能量守恒。数值实验结果表明，与Crank-Nicolson格式和紧差分格式相比，向前Euler格式长时间计算的稳定性稍差，但是其计算效率更高。另外，在数值上，Crank-Nicolson格式和紧差分格式能够精确地保持离散的电荷和能量守恒，验证了理论结果的正确性。

通过对3种格式的比较，可以看出它们在求解KGS方程时的优缺点，为不同工程应用提供合适的选择。

参考文献：

［1］ FUKUDA I，TSUTSUMI M.On coupled Klein-Gordon-Schr?dinger equations Ⅱ［J］.Journal of Mathematical Analysis and Applications，1978，66（2）：358-378.DOI：10.1016/0022-247X（78）90239-1.

［2］ BAILLON J B，CHADAM J M.The cauchy problem for the coupled Schr?dinger-Klein-Gordon equations［J］.North-Holland Mathematics Studies，1978，30：37-44.DOI：10.1016/S0304-0208（08）70857-0.

［3］ DARWISH A，FAN Engui.A series of new explicit exact solutions for the coupled Klein-Gordon-Schr?dinger equations［J］.Chaos，Solitons and Fractals，2004，20（3）：609-617.DOI：10.1016/S0960-0779（03）00419-3.

［4］ WANG Mingliang，ZHOU Yubin.The periodic wave solutions for the Klein-Gordon-Schr?dinger equations［J］.Physics Letters A，2003，318（1/2）：84-92.DOI：10.1016/j.physleta.2003.07.026.

［5］ WANG Baoxiang.Classical global solutions for nonlinear Klein-Gordon-Schr?dinger equations［J］.Mathematical Methods in the Applied Sciences，1997，20（7）：599-616.DOI：10.1002/（SICI）1099-1476（19970510）20：7<599：：AID-MMA866>3.0.CO；2-7.

［6］ CAVALCANTI M，CAVALCANTI V.Global existence and uniform decay for the coupled Klein-Gordon-Schr?din ger equations［J］.Nonlinear Differential Equations and Applications，2000，7（3）：285-307.DOI：10.1007/PL0000 1426.

［7］ HAYASHI N，WAHL W.On the global strong solutions of coupled Klein-Gordon-Schr?dinger equations［J］.Journal of the Mathematical Society of Japan，1987，39（3）：489-497.DOI：10.2969/jmsj/03930489.

［8］ OHTA M.Stability of stationary states for the coupled Klein-Gordon-Schr?dinger equations［J］.Nonlinear Analysis： Theory，Methods and Applications，1996，27（4）：455-461.DOI：10.1016/0362-546X（95）00017-P.

［9］ FUKUDA I，TSUTSUMI M.On the Yukawa-coupled Klein-Gordon-Schr?dinger equations in three space dimensions［J］.Proceedings of the Japan Academy Series A Mathematical Sciences，1975，51（6）：402-405.DOI：10.3792/pja/1195518563.

［10］ XIA Jingna，HAN Shuxia，WANG Mingliang.The exact solitary wave solutions for the Klein-Gordon-Schr?dinger equations［J］.Applied Mathematics and Mechanics，2002，23（1）：58-64.DOI：10.1007/BF02437730.

［11］ WANG Tingchun.Optimal point-wise error estimate of a compact difference scheme for the Klein-Gordon-Schr? dinger equation［J］.Journal of Mathematical Analysis and Applications，2014，412（1）：155-167.DOI：10.1016/j.jmaa.2013.10.038.

［12］ HONG Jialin，JIANG Shanshan，LI Chun.Explicit multi-symplectic methods for Klein-Gordon-Schr?dinger equations［J］.Journal of Computational Physics，2009，228（9）：3517-3532.DOI：10.1016/j.jcp.2009.02.006.

［13］ WANG Junjie，XIAO Aiguo.Conservative Fourier spectral method and numerical investigation of space fractional Klein-Gordon-Schr?dinger equations［J］.Applied Mathematics and Computation，2019，350：348-365.DOI：10.1016/j.amc.2018.12.046.

［14］ WANG Tingchun，ZHAO Xiaofei，JIANG Jiaping.Unconditional and optimal H2-error estimates of two linear and conservative finite difference schemes for the Klein-Gordon-Schr?dinger equation in high dimensions［J］.Advances in Computational Mathematics，2018，44：477-503.DOI：10.1007/s10444-017-9557-5.

［15］ ZHANG Luming.Convergence of a conservative difference scheme for a class of Klein-Gordon-Schr?dinger equations in one space dimension［J］.Applied Mathematics and Computation，2005，163（1）：343-355.DOI：10.1016/j.amc.2004.02.010.

［16］ KONG Linghua，WANG Lan，JIANG Shanshan，et al.Multi-symplectic Fourier pseudo-spectral integrators for Klei n-Gordon-Schr?dinger equations［J］.Science China Mathematics，2013，56：915-932.DOI：10.1007/s11425-013-4575-3.

［17］ XIANG Xinmin.Spectral method for solving the system of equations of Schr?dinger-Klein-Gordon field［J］.Journal of Computational and Applied Mathematics，1988，21（2）：161-171.DOI：10.1016/0377-0427（88）90265-8.

［18］ WANG Tingchun，ZHAO Xiaofei.Unconditional L∞-convergence of two compact conservative finite difference schemes for the nonlinear Schr?dinger equation in multi-dimensions［J］.Calcolo，2018，55（3）：34-59.DOI：10.1007/s10092-018-0277-0.

［19］ WANG Jialing，LIANG Dong，WANG Yushun.Analysis of a conservative high-order compact finite difference scheme for the Klein-Gordon-Schr?dinger equation［J］.Journal of Computational and Applied Mathematics，2019，358：84-96.DOI：10.1016/j.cam.2019.02.018.