求解耦合非线性Schr?dinger-Boussinesq方程的三角标量辅助变量方法

郭姣姣 庄清渠

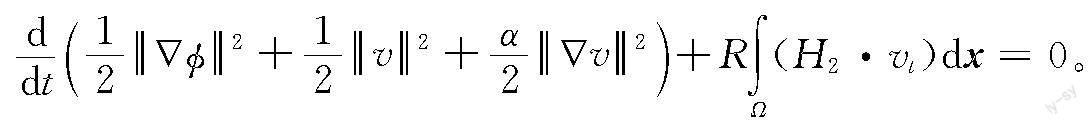
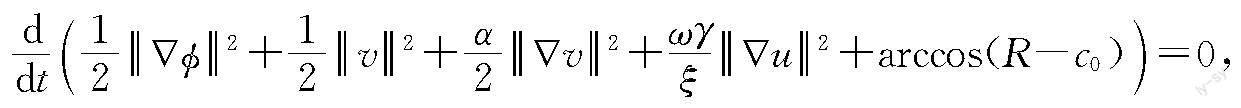
摘要： 采用三角标量辅助变量（TSAV）方法，构造求解耦合非线性Schr?dinger-Boussinesq方程初边值问题的高效数值格式。基于方程非线性势能的三角函数形式，提出求解方程的TSAV格式；对方程在时间和空间上分别采用二阶Crank-Nicolson格式和傅里叶谱方法进行离散，并证明时间半离散格式的修正能量守恒律。最后，通过数值算例对文中格式进行验证。结果表明：文中格式具有有效性，修正能量具有守恒性。

关键词： 耦合非线性Schr?dinger-Boussinesq方程； 三角标量辅助变量方法； 修正能量； 守恒律

中图分类号： O 241.8文献标志码： A   文章编号： 1000-5013（2024）01-0098-10

Trigonometric Scalar Auxiliary Variable Method for Coupled Nonlinear Schr?dinger-Boussinesq Equation

GUO Jiaojiao， ZHUANG Qingqu

（School of Mathematical Sciences， Huaqiao University， Quanzhou 362021， China）

Abstract： Based on the trigonometric scalar auxiliary variable （TSAV） method， an efficient numerical scheme is constructed to solve the initial boundary value problem of the coupled nonlinear Schr?dinger-Boussinesq equation. Firstly， based on the trigonometric function form of the nonlinear potential energy equation， the TSAV scheme of the considered equation is proposed. Then， the equation is discretized in temporal and spatial by using the second-order Crank-Nicolson scheme and Fourier spectral method respectively， and the modified energy conservation law of time semi-discrete scheme is proved. Finally， the proposed scheme is verified by numerical examples. The results show that the proposed scheme is effective and the modified energy is conserved.

Keywords：coupled nonlinear Schr?dinger-Boussinesq equation； trigonometric scalar auxiliary variable method； modified energy； conservation law

Schr?dinger方程和Boussinesq方程是应用数学和物理学中的重要方程，前人对这两类方程展开了广泛的研究［1-2］。耦合非线性Schr?dinger-Boussinesq（CNSB）方程是一类用于描述激光和等离子体领域各种物理过程的重要的波动方程［3］。文献［4-5］对方程解析解的存在性、全局光滑解及适定性进行了研究。由于直接求解CNSB方程的困难较大，所以数值求解CNSB方程得到了广泛的关注。例如，Yang等［6］设计了求解CNSB方程的BDF2-Galerkin有限元格式。Tian等［7］设计了基于Galerkin有限元框架的时间两网格格式。 Oruc［8］提出一种用于求解CNSB方程的径向基函数结合有限差分的无网

格逼近方法。Cai等［9］针对CNSB方程构造了一种保持质量和能量守恒的快速求解器。文献［10-11］对一维和二维CNSB方程构造一类保能量和质量守恒的有限差分方法。关于求解CNSB方程的一系列线性和非线性的紧致有限差分格式及其稳定性、收敛性等理论分析可参考文献［12-13］。二次B样条有限元方法［14］、基于时间分裂的傅里叶谱方法［15］及标量辅助变量（SAV）方法［16］等均可用于高效求解CNSB方程。

SAV方法首先由Shen等［17］提出，之后出现了基于SAV方法的各类扩展形式，如拉格朗日乘数法、指数标量辅助变量方法等，这些方法因计算的高效性和简便性受到了广泛的应用［18］。Yang等［19］提出一种基于非线性势能泛函的三角函数形式，即三角标量辅助变量（TSAV）方法，并验证该方法可以成功应用于一大类梯度流模型。该方法继承了传统SAV方法所有优点的同时，还弥补了其不足，它对于任意非线性势能泛函，均可通过添加一个大于1的常数c0，使新引入的标量辅助变量具有常正性。将标量辅助变量作用于方程的非线性部分，可以使方程完全解耦，简便计算。文献［20-21］基于正弦函数型标量辅助变量，分别构建了四階非线性波动方程和广义分数阶Schr?dinger方程的高阶TSAV保能格式。目前，针对CNSB方程的高阶TSAV保能格式的研究仍较少。基于此，本文基于余弦函数型标量辅助变量，提出一种求解耦合非线性Schr?dinger-Boussinesq方程的高效能量稳定方法。

1 问题与TSAV格式

考虑带周期边界条件的CNSB方程的数值求解格式，即

式（1）中：i2=-1；Ω=［a，b］d，d=1，2；ε表示电子数与离子数质量比的参数，ε>0；γ，ξ，α，θ，ω均为正实数；f（v）为一个满足f（0）=0的充分光滑函数；u（x，t）为朗缪尔振荡电场的复值函数；v（x，t）为描述低频密度摄动的实值函数。

式（1）的初始条件为u（x，0）=u0（x），v（x，0）=v0（x），vt（x，0）=v1（x），x∈Ω。

式（1）满足电荷（Q）守恒律和能量（E）守恒律［15］，有

将式（1）中的第1个方程与u作内积，取虚部，可证明电荷守恒律。将式（1）中的第1个方程与-ut作内积，取实部，再将式（1）中的第2个方程与-vt作内积，结合上述内积结果和vt=Δφ，可证明能量守恒律。

采用TSAV方法对式（1）进行求解，首先，引入vt=Δφ，将式（1）降阶为关于时间一阶导的等价形式，有

此时，式（2）的初始条件和边界条件可分别表示为

u（x，0）=u0（x）， v（x，0）=v0（x）， φ（x，0）=φ0（x），  x∈Ω，

u（a，t）=u（b，t）， v（a，t）=v（b，t）， φ（a，t）=φ（b，t），  t∈（0，T］。

其次，对于任意网格函数u1，u2∈L2（Ω），定义内积（·，·）和范数·的表达式为

然后，基于方程的非线性势能引入三角标量辅助变量，有

式中：c0是一个恒大于1的常数，则有

基于此，可构建式（2）的TSAV格式，有

其中有

定理1 式（3）满足修正能量守恒律，有

将式（3）中第2，3个方程分别与vt，-φt作内积并相加，可得

将上述两个内积结果相加，并结合式（3）中最后一个方程，可得

即可证得式（4）。证明完毕。

2 时间半离散格式

对于n=1，2，…，N-1，为了求解un+1，vn+1，φn+1，Rn+1，通过二阶Crank-Nicolson格式构建CNSB方程的时间半离散格式，有

此外，式（5）的实现需要第1层的值u1，v1，φ1，R1和初始条件。初始条件是已知的，则当n=0时，第1层的值可通过隐式Crank-Nicolson格式求解，有

定理2 时间半离散格式（5），（6）满足修正能量守恒律，有

在式（5）第2，3个方程的两端分别乘以（vn+1-vn），-（φn+1-φn），然后，在Ω上积分，再将结果相加，整理可得

将以上两个等式相加，并利用式（5）中最后一个方程，可得

下面考虑式（5），（6）的求解。首先，考虑将式（5）的前3个方程分别改写为

最后，将求得的un+1，vn+1代入式（5）中最后一个方程，可得

值得注意的是，余弦函数的定义域为全体实数，且通过计算可知Γ的值恒为实数，所以Rn+1是始终可解的。

此外，初始值u1，v1，φ1，R1可通过式（6）采用预估校正法进行类似的求解。简言之，TSAV格式（5），（6）可以通过以下4个步骤快速求解：

1） 通过式（6）解得第1层的值u1，v1，φ1，R1；

2） 计算b1，b2，b3；

3） 依次从式（7），（10），（11）求解un+1，vn+1，φn+1；

4） 由式（12）解得Rn+1。

3 数值算例

为了方便求解，对所有数值实验均采用快速傅里叶变换（FFT）和傅里叶逆变换（IFFT）进行空间离散，以验证文中格式在时间方向上具有二阶精度，在空间方向上具有谱精度，有效保持修正能量E的守恒性，并模拟CNSB方程二维孤立波的演化行为。在此之前，先定义enj（g）=gnj-g（xj，tn），则对应的L∞误差和L2误差可分别表示为

式中：任意网格函数g可分别表示u，v，φ。

L∞误差和L2误差对应的收敛阶Rate的计算公式分别为

当t=0时，式（13）可作为CNSB方程的初始条件，取常数c0=2.0。

检验文中格式的时间精度和空间精度。选择计算区域Ω=［-20，20］，T=1。固定空间剖分M=512。

不同时间步长下u，v，φ的时间L∞ 误差及收敛阶，时间L２ 误差及收敛阶，分别如表1，2所示。

表1，2中：Rate∞，u，Rate∞，v，Rate∞，φ分別为Err∞（u），Err∞（v），Err∞（φ）的收敛阶；

Rate2，u，Rate2，v，Rate2，φ分别为Err2（u），Err2（v），Err2（φ）的收敛阶。

由表1，2可知：文中格式在时间方向上具有二阶精度。

固定时间步长τ=0.000 1，u，v，φ在不同空间剖分下的空间L∞误差和L2误差，分别如图1所示。由图1可知：文中格式在空间方向上呈现指数收敛，具有谱精度。

选取计算区域Ω=［-20，140］，T=100，固定空间剖分M=512，时间步长τ=0.01。u，v，φ的精确解与数值解，如图2所示。

由图2可知：不同时刻下的数值解与精确解都能很好地吻合，故文中提出的TSAV格式是稳定的。

验证CNSB方程的守恒律，基于上述计算区域和网格设计，修正能量（E）和修正能量误差（enE）随着时间的变化情况，如图3所示。

由图3可知：TSAV格式能很好地保持修正能量守恒，这与节2的能量守恒定理一致。

在不同时间步长τ=1/100，1/200，1/400下，电荷误差（enQ）和能量误差（enE）随着时间的变化情况，如图4所示。由图4可知：电荷误差和能量误差均随着时间步长的减小而减小。

算例2 考慮CNSB方程二维孤立波的演化行为，选择初始条件，有［7，15］

计算区域取Ω=［-20，20］2，固定空间剖分和时间步长分别为M=512，τ=0.01，取常数c0=2.0。

CNSB方程在情况1下的数值解u，v，φ不同时间的曲面图，如图5所示。

由图5可知：u的数值解随着时间的推移，由一个波峰变成多个波峰；v，φ的数值解逐渐呈现下陷趋势，且逐渐产生少量余波。

CNSB方程在情况2下可以简化为Zakharov系统，它是CNSB方程的一种特殊形式。二维Zakharov系统的数值解u，v，φ不同时间的曲面图，如图6所示。

由图6可知：u的数值解随着时间的演化过程与情况1类似；v的数值解也随着时间推移出现下陷趋势，但形态与情况1不同；φ随着时间的推移并未出现下陷趋势，也无余波产生。这与文献［7］中算例4.3的研究结果一致。

综上可知，文中TSAV格式可推广至方程高维问题的求解。

4 结束语

利用TSAV方法构造耦合非线性Schr?dinger-Boussinesq方程的能量稳定数值求解格式，理论证明了时间半离散格式的修正能量守恒性。通过数值实验验证了格式的稳定性和有效性，并模拟了方程二维的动力学过程。

参考文献：

［1］ CHAE D.Global regularity for the 2D Boussinesq equations with partial viscosity terms［J］.Advances in Mathematics，2006，203（2）：497-513.DOI：10.1016/j.aim.2005.05.001.

［2］ 孙传志，汪佳玲.非线性薛定谔方程的几种差分格式［J］.华侨大学学报（自然科学版），2021，42（4）：551-560.DOI：10.11830/ISSN.1000-5013.202011019.

［3］ MAKHANKOV V G.On stationary solutions of the Schr?dinger equation with a self-consistent potential satisfying Boussinesq′s equation［J］.Physics Letters A，1974，50（1）：42-44.DOI：10.1016/0375-9601（74）90344-2.

［4］ GUO Boling，DU Xianyun.Existence of the periodic solution for the weakly damped Schr?dinger-Boussinesq equation［J］.Journal of Mathematical Analysis and Applications，2001，262（2）：453-472.DOI：10.1006/jmaa.2000.7455.

［5］ FARAH L G，PASTOR A.On the periodic Schr?dinger-Boussinesq system［J］.Journal of Mathematical Analysis and Applications，2010，368（1）：330-349.DOI：10.1016/j.jmaa.2010.03.007.

［6］ YANG Yining，SUN Ziyu，LIU Yang，et al.Structure-preserving BDF2 FE method for the coupled Schr?dinger-Boussinesq equations［J］.Numerical Algorithms，2023，93（3）：1243-1267.DOI：10.1007/s11075-022-01466-w.

［7］ TIAN Jiale，SUN Ziyu，LIU Yang，et al.TT-M finite element algorithm for the coupled Schr?dinger-Boussinesq equations［J］.Axioms，2022，11（7）：314.DOI：10.3390/axioms11070314.

［8］ ORUC O.A local radial basis function-finite difference （RBF-FD） method for solving 1D and 2D coupled Schr?dinger-Boussinesq （SBq） equations［J］.Engineering Analysis with Boundary Elements，2021，129：55-66.DOI：10.1016/j.enganabound.2021.04.019.

［9］ CAI Jiaxiang，YANG Bin，ZHANG Chun.Efficient mass-and energy-preserving schemes for the coupled nonlinear Schr?dinger-Boussinesq system［J］.Applied Mathematics Letters，2019，91：76-82.DOI：10.1016/j.aml.2018.11.024.

［10］ DENG Dingwen，WU Qiang.Analysis of the linearly energy-and mass-preserving finite difference methods for the coupled Schr?dinger-Boussinesq equations［J］.Applied Numerical Mathematics，2021，170：14-38.DOI：10.1016/j.apnum.2021.07.013.

［11］ DENG Dingwen，WU Qiang.Linearized and decoupled structure-preserving finite difference methods and their analyses for the coupled Schr?dinger-Boussinesq equations［J］.Numerical Methods for Partial Differential Equations，2021，37（5）：2924-2951.DOI：10.1002/num.22805.

［12］ LIAO Feng，ZHANG Luming，WANG Tingchun.Two energy-conserving and compact finite difference schemes for two-dimensional Schr?dinger-Boussinesq equations［J］.Numerical Algorithms，2020，85：1335-1363.DOI：10.1007/s11075-019-00867-8.

［13］ LIAO Feng，ZHANG Luming.Numerical analysis of a conservative linear compact difference scheme for the coupled Schr?dinger-Boussinesq equations［J］.International Journal of Computer Mathematics，2018，95（5）：961-978.DOI：10.1080/00207160.2017.1302082.

［14］ BAI Dongmei，ZHANG Luming.The quadratic B-spline finite-element method for the coupled Schr?dinger-Boussinesq equations［J］.International Journal of Computer Mathematics，2011，88（8）：1714-1729.DOI：10.1080/00207160.2010.522234.

［15］ LIAO Feng，ZHANG Luming，WANG Shanshan.Time-splitting combined with exponential wave integrator Fourier pseudospectral method for Schr?dinger-Boussinesq system［J］.Communications in Nonlinear Science and Numerical Simulation，2018，55：93-104.DOI：10.1016/j.cnsns.2017.06.033.

［16］ HE Yuyu，CHEN Hongtao.Efficient and conservative compact difference scheme for the coupled Schr?dinger-Boussinesq equations［J］.Applied Numerical Mathematics，2022，182：285-307.DOI：10.1016/j.apnum.2022.08.013.

［17］ SHEN Jie，XU Jie，YANG Jiang.The scalar auxiliary variable （SAV） approach for gradient flows［J］.Journal of Computational Physics，2018，353：407-416.DOI：10.1016/j.jcp.2017.10.021.

［18］ 郭姣姣，莊清渠.求解耦合非线性Klein-Gordon-Schr?dinger方程的能量稳定方法［J］.华侨大学学报（自然科学版），2023，44（4）：533-540.DOI：10.11830/ISSN.1000-5013.202206030.

［19］ YANG Junxiang，KIM J.The stabilized-trigonometric scalar auxiliary variable approach for gradient flows and its efficient schemes［J］.Journal of Engineering Mathematics，2021，129（1）：18.DOI：10.1007/s10665-021-10155-x.

［20］ TIAN Zhihui，RAN Maohua，LIU Yang.Higher-order energy-preserving difference scheme for the fourth-order nonlinear strain wave equation［J］.Computers Mathematics with Applications，2023，135：124-133.DOI：10.1016/j.camwa.2023.01.026.

［21］ ZHANG Xi，RAN Maohua，LIU Yang，et al.A high-order structure-preserving difference scheme for generalized fractional Schr?dinger equation with wave operator［J］.Mathematics and Computers in Simulation，2023，210：532-546.DOI：10.1016/j.matcom.2023.03.027.