基于聚类和随机搜索优化的核反应堆数字孪生参数反演模型

龙家雨,宋美琪,*,柴 翔,刘晓晶,妥艳洁,3

(1.上海交通大学 智慧能源创新学院,上海 200240;2.上海交通大学 机械与动力工程学院,上海 200240;3.国家电力投资集团有限公司,北京 100029)

数字孪生(digital twin)是以数字化方式创建物理实体的虚拟模型,充分利用物理模型、传感器、运行历史等数据,集成多学科、多尺度对物理实体在现实环境中的行为进行模拟的仿真过程。作为虚拟空间中对实体产品的镜像,其反映了相对应物理实体产品的全生命周期过程[1-2]。核电数字孪生有利于核电站以较低成本实现高可靠性、可用性与可维护性[3],可在核电站的预测性运行与维护、自主运行与控制等领域发挥作用,如实现小型模块化反应堆自动、自主和实时性能要求[4]或结合先进PSA(概率风险评估)方法构建实时决策支持系统[5]等。

核电站为实时监测运行状态而布置大量的传感器,产生的数据种类多、总量大,造成存储空间需求大、传输效率不高、数据分析复杂度高等问题,基于核电站构建的数字孪生系统同样面临此类问题,如何优化传感器的布置也需要进一步研究。核电领域常采用数据降维与反向求解的特征工程进行数据处理与分析[6-7]。Peng等[8]利用稀疏自动编码器(sparse auto encoder)对仿真程序PCTRAN模拟的核电站的几种不同瞬态参数提取特征,实现对核电站异常状态的检测。Yang等[9]用一维卷积神经网络(CNN)重建核电站传感器信号,通过逐步减少传感器进行实验,在16种传感器数据确定了5种影响最大的参数。李翔宇等[10]通过改进特征工程算法建立了一种核电站瞬态运行参数数据压缩和数据复原方法,结合主成分分析法与高斯回归过程方法对秦山300 MWe全范围仿真机产生的瞬态运行数据进行压缩与高精度复原。

目前此类研究在特征提取上面临如下的问题:通过逐次实验的方式获取特征参数,依赖长期数据,运算量大、效率较低;采用主成分分析等方式进行数据压缩,在压缩过程中改变了原参数的值,虽然提升了传输效率且能达到很高精度,但也因此失去了特征参数的可解释性。

针对上述问题,本文基于多物理场耦合程序实现空间热离子反应堆虚拟模型的构建并获取数字孪生数据,结合K-means聚类算法与ANN(人工神经网络),提出一种能够在保留原数据的情况下高效提取特征参数并对其他非特征参数进行反演的方法,对空间热离子反应堆堆芯的4个区域的温度参数分别建立参数反演模型并取得较高精度的反演结果。

1 数据集建立

本文的参数反演模型是对空间热离子反应堆的数字孪生堆芯温度数据建立的。对堆芯物理系统的数字孪生计算通过上海交通大学搭建的多物理场耦合数值模拟平台[11]完成。

1.1 空间热离子堆堆芯系统

与常规压水堆相比,空间热离子反应堆体形较小,堆芯三维几何模型如图1所示。空间热离子反应堆由37根热离子燃料元件和ZrH慢化剂芯块组成。通过旋转控制鼓引入反应性,从而启动空间热离子反应堆。燃料热量产生与传递过程如下:燃料芯块发生核裂变反应,产生热量,热量通过发射极、接收极、气隙传递给冷却剂,冷却剂通过对流换热将会带走部分热量,剩余热量传递给慢化剂芯块,慢化剂通过热辐射向太空散失部分热量。

图1 空间热离子反应堆堆芯的几何模型[11]Fig.1 Geometric model of space thermionic reactor core[11]

空间热离子反应堆堆芯中最核心的部件是热离子燃料元件,其结构示于图2。热离子燃料元件为单节全长多层套筒结构的热离子燃料元件,采用高浓缩UO2作为燃料,NaK-78作为冷却剂。发射极材料为单晶钼和化学气相沉积制成的钨表面层,接收极由多晶钼制成,接收极外包有Al2O3绝缘体薄层。

图2 单节热离子燃料元件[11]Fig.2 Single-section thermionic fuel element[11]

1.2 数据获取

使用基于OpenFOAM开发的多物理场耦合程序对空间热离子反应堆构建数值模拟平台。网格划分、工况设置、相关方程及计算可见文献[11]。基本参数的程序计算值与设计值吻合良好,在设计范围内。

20%热管失效工况下的仿真结果中包含燃料、发射极、接收极、冷却剂4个区域的温度计算结果,采样时间间隔为0.1 s,瞬态计算从750 s开始到2 425 s结束,共16 750个时间节点。沿燃料元件轴向(z轴)均匀分布的100个测点,高度从0到0.375 m。剔除最初原始数据发生突变的时间点,最终生成了16 748×1 601维的数据集,对应1 600个参数的16 748个时间节点。

用相同的方式获取15%热管失效工况下的堆芯温度数据,包含从750.2 s到1 893.9 s共11 438个时间节点,参数种类与20%热管失效工况下的相同,将用于参数反演模型的效果验证。

2 参数反演模型构建

本文构建的参数反演模型结构如图3所示。不同于自动编码器与数据压缩复原方法,本文构建的模型在特征提取环节通过机器学习方法快速选取出特征参数并且保留了其原始数据。

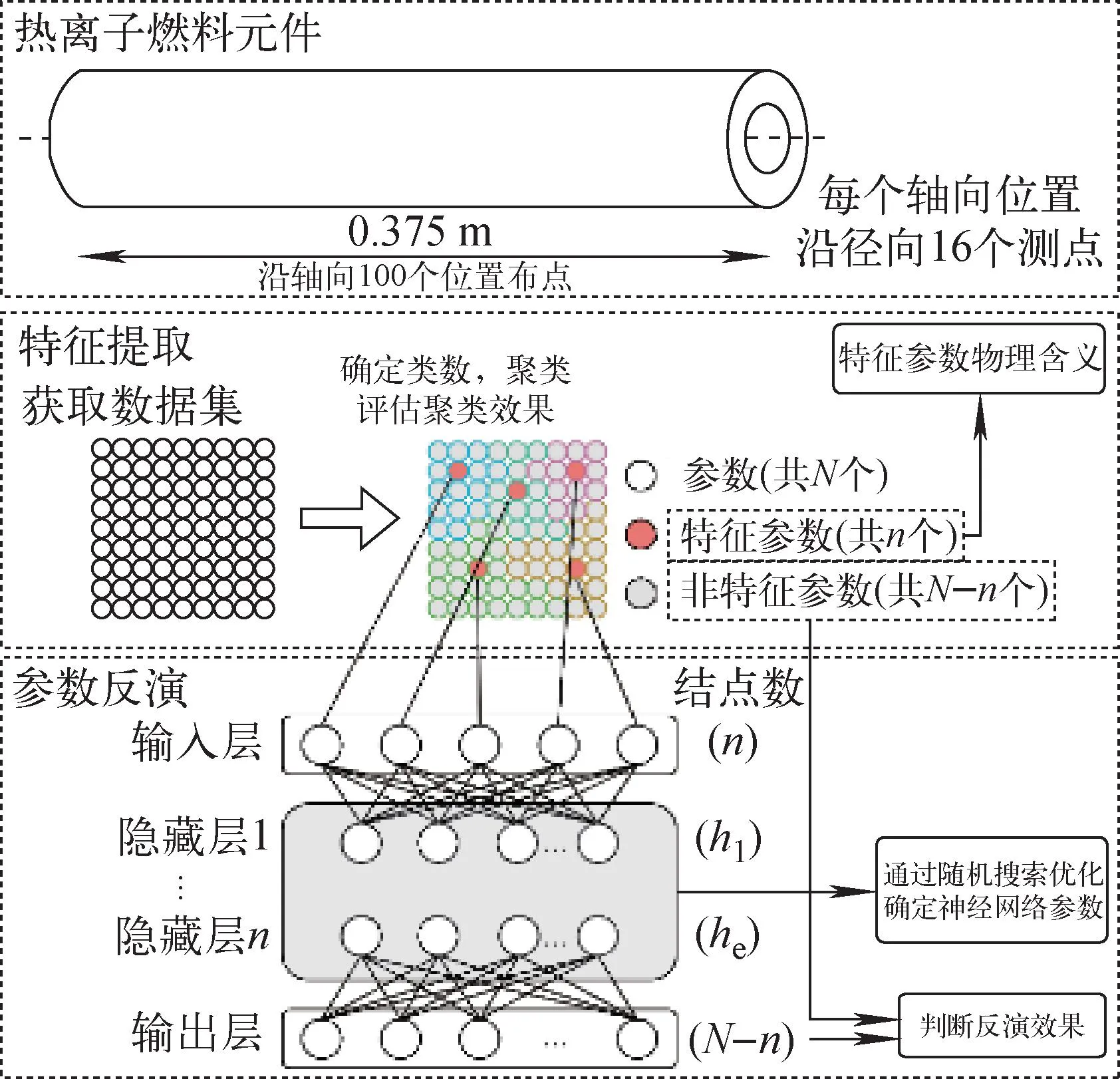
图3 本文的参数反演模型Fig.3 Parameter inversion model proposed in this paper

依据如图4所示流程构建参数反演模型,包括特征提取与神经网络搭建两部分,并在最后进行模型效果验证。

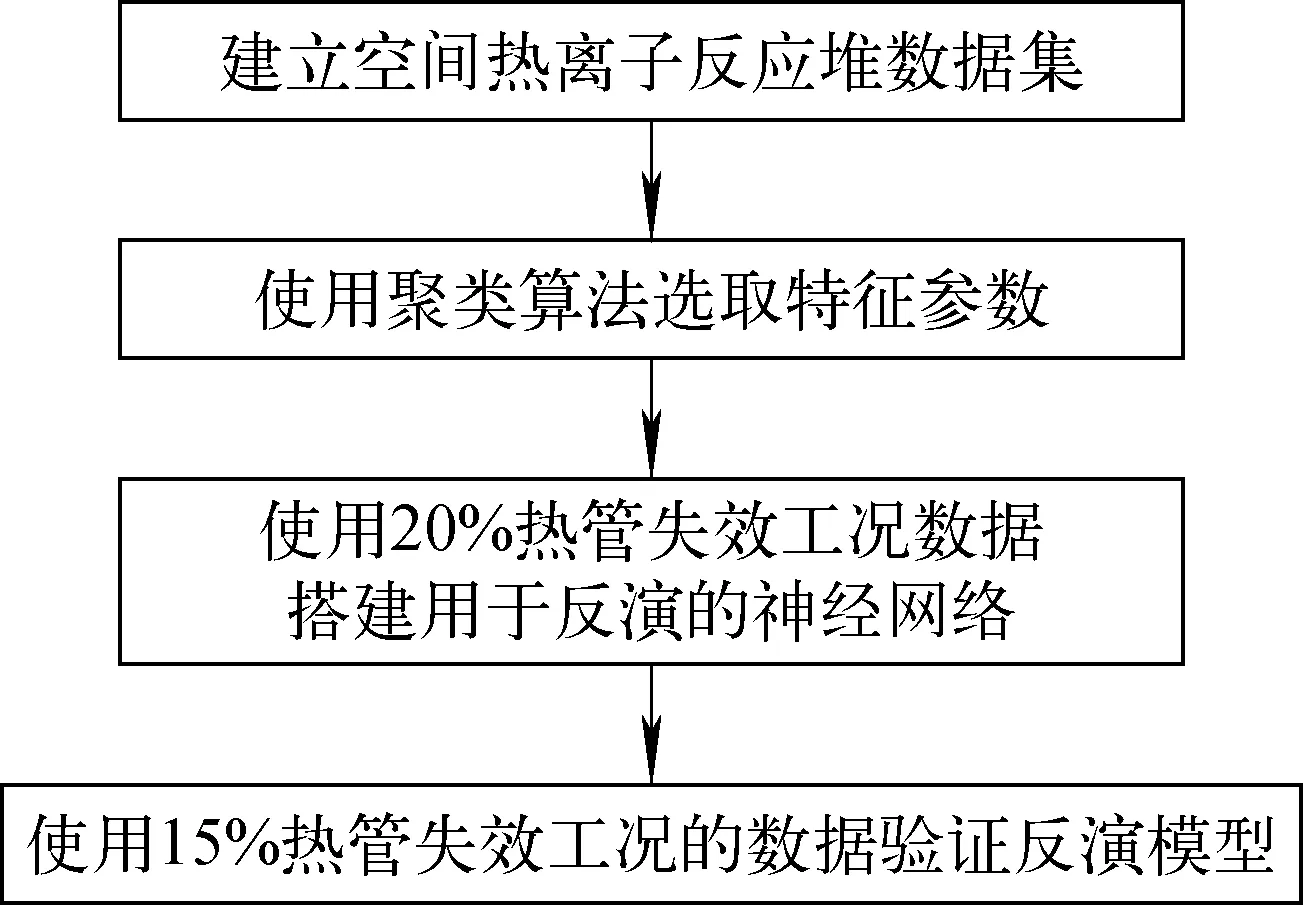
图4 参数反演模型搭建流程Fig.4 Process of constructing parameter inversion model

2.1 基于K-means的特征选取环节

特征选取是一个数据降维环节,将原始数据转换为低维度的特征向量,从而提高数据传输与分析效率,也节约了存储空间。K均值聚类算法(K-means算法)是一种无监督的分类方法,在设定聚类数后可自动通过算法完成不同参数类别的划分。不同类簇中的中心参数表征了该类参数中的典型值,选择到聚类中心有最小平方欧氏距离的参数作为特征参数。由此,通过K-means聚类可以高效选取特征参数。聚类数的选择影响着聚类最终效果的好坏,选择轮廓系数(silhouette coefficient)作为评估聚类效果的指标,并比较不同聚类数的轮廓系数以选择最佳聚类数。

特征选取环节包括如下步骤:将空间热离子反应堆的数字孪生数据归一化、使用K-means算法分类、使用轮廓系数指标评估聚类效果、提取各类最接近聚类中心的参数作为特征参数,流程如图5所示。

图5 特征提取流程Fig.5 Process of feature extraction

首先,分别对4个位置的温度参数进行归一化处理,将数据映射到[0,1]之间。使用如下公式:

(1)

K-means算法的核心思想是找出K个聚类中心c1,c2,…,cK,使得每个数据点xi和与其最近的聚类中心cv的平方距离和被最小化(该平方距离和被称为偏差D)[12],主要步骤[13]如下。

1) 聚类中心初始化:随机指定K个聚类中心c1,c2,…,cK。

2) 对样本归类:每个样本xi仅选择1个聚类中心S(t)作为归属,找到与它具有最小平方欧氏距离的聚类中心cv,并将其分配到所标明的类cv:

∀n,1≤n≤K}

(2)

3) 更新聚类中心cn:将每个cn移动到其标明的类的中心:

(3)

4) 计算偏差D:

(4)

5) 判断偏差D是否收敛:如果D收敛,则返回c1,c2,…,cK并终止本算法;否则,返回步骤2。

轮廓系数是用来评估聚类效果好坏的一种指标,衡量聚类中样本的内聚度和分离度。内聚度ai为第i个样本到同簇中其他点的距离的平均值,分离度bi为第i个样本到其他簇中点的距离的平均值,第i个样本的轮廓系数[14]为:

(5)

式中:Si越接近1,说明样本i的聚类合理;Si为0时,说明样本i处于两簇的边界;Si为-1时,说明样本i应该被分到其他的簇。对所有样本的轮廓系数取平均值,得到聚类结果的总轮廓系数。

以接收极为例,轮廓系数随聚类数的变化如图6所示。在聚类数为31时,轮廓系数达到最大,表明类数选为31类时的聚类效果最好。

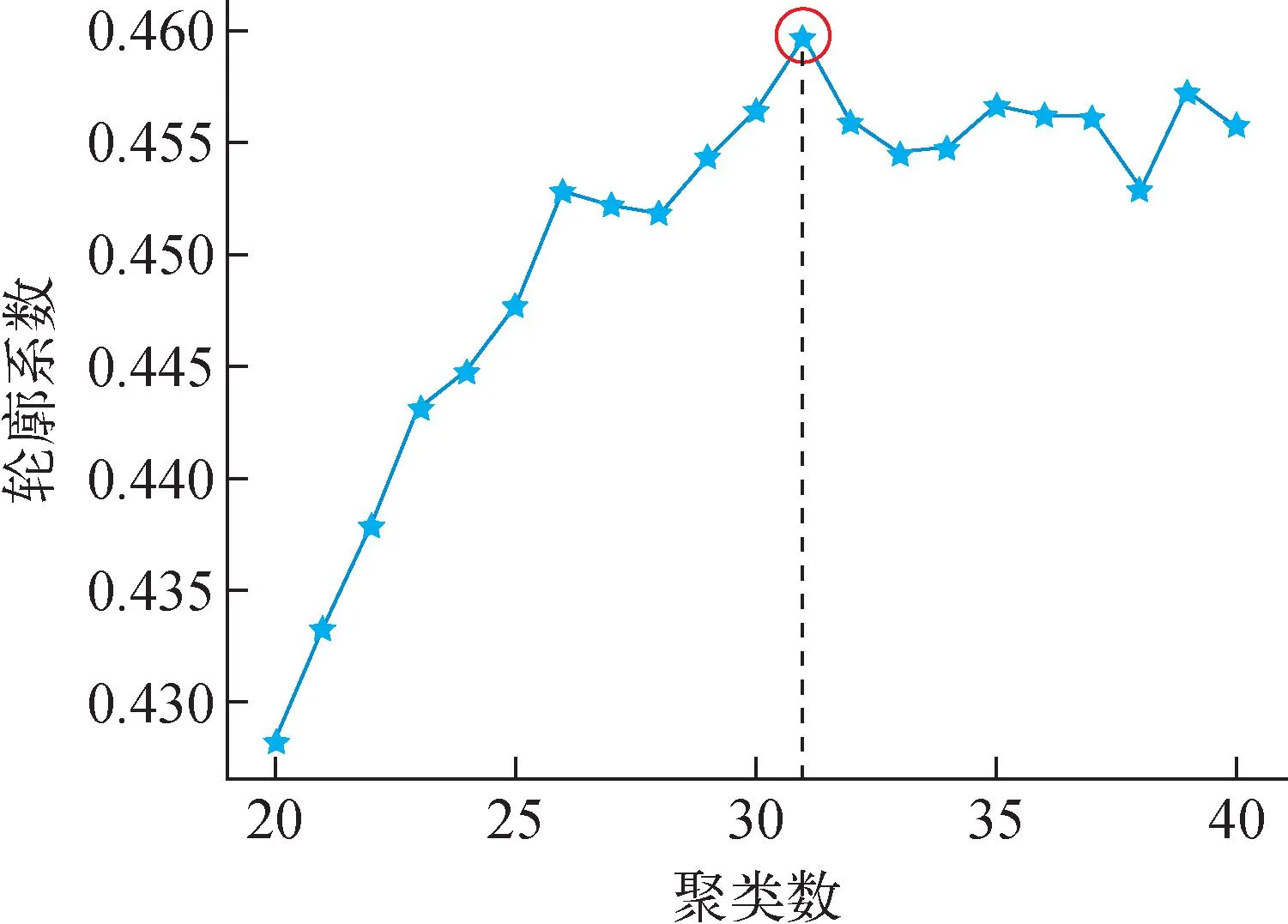
图6 接收极的轮廓系数随聚类数的变化Fig.6 Variation of silhouette coefficient of receiving pole with number of clusters

确定聚类数后,选取每类中到聚类中心平均距离最小的参数曲线作为特征参数,保存特征索引。参数索引与几何位置一一对应,其中轴向方向序号z-1～z-100分别代表0.003 75 m的整数倍,如z-3代表轴向0.003 75 m×3处位置;径向方向序号r-1代表径向中心处,r-2、r-3、r-4分别代表3个不同径向位点。仍以接收极为例,提取的31个特征参数的对应位点列于表1。

从表1可看出,特征参数沿轴向分布较为均匀,在径向分布上,位于中心与4号径向位点的特征参数占所有特征参数的74.2%,表明这两个径向位点的参数值得关注。由于上述特征参数均可在堆芯中确定其所属位置,因此也可确认每个特征参数的含义。

对各区域分别进行聚类,4个区域的聚类数最终确定如表2所列。重复上述流程,得到4个区域的特征参数及其对应的位点信息。将特征参数与非特征参数重新编排为新的数据集,用于下一步的参数反演。

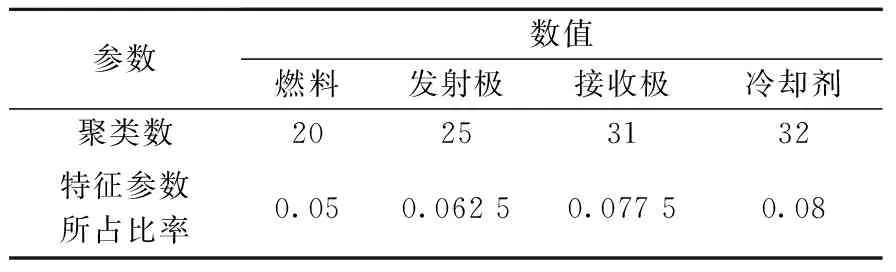
表2 不同区域的聚类数Table 2 Clusteringnumbers of different regions

2.2 搭建神经网络反演模型

完成对数据的降维后,需要进行反向求解,通过使用降维后的数据求出对应的物理场分布与相应探测器的理论测量值,从而完成数据的反演。本文为4个区域分别搭建全连接神经网络进行参数反演,并使用随机配置法优化神经网络结构和学习率,根据各区域的反演结果评估参数反演模型。

神经网络的计算单元完成输入xi与权重wi的加权求和,添加偏置bi并经过激活函数Φ得到输出yi,构成下一层的输入或者最终的输出[15],如下式:

(6)

全连接代表每个神经元与相邻层的所有神经元相连,且同层中的神经元互不连接。选择MSE(均方差)作为损失函数,以欧氏距离表达反演的预测值yi与真实值y′i的距离:

(7)

使用SGD(随机梯度下降)函数,通过反向传播更新神经网络权值,每个连接的权值通过自身减去学习率与损失函数对该权值的一阶偏导数进行更新。使用原始数据输入神经网络,温度值的范围在[750 ℃,2 500 ℃],由此选择神经网络各隐藏层的激活函数为Leaky-ReLU。将16 748个时间节点数据按12 000∶2 000∶2 748的比例划分为训练集、验证集、测试集,在前14 000个时间节点中按照12 000∶2 000的比例随机划分为训练集与验证集。收敛条件设置为两轮MSE之差小于1×10-6且MSE<100。以接收极为例,初步搭建神经网络。经尝试,当学习率大于1×10-7时训练易发散。采用1×10-7的学习率、网络结构为3层、每层各20个节点的全连接神经网络,设置1 500轮训练。损失随迭代轮数的变化如图7所示,最终训练集与验证集损失分别为0.716 4和0.844 8。然后围绕上述参数,对学习率、神经网络层数与节点数进行优化。

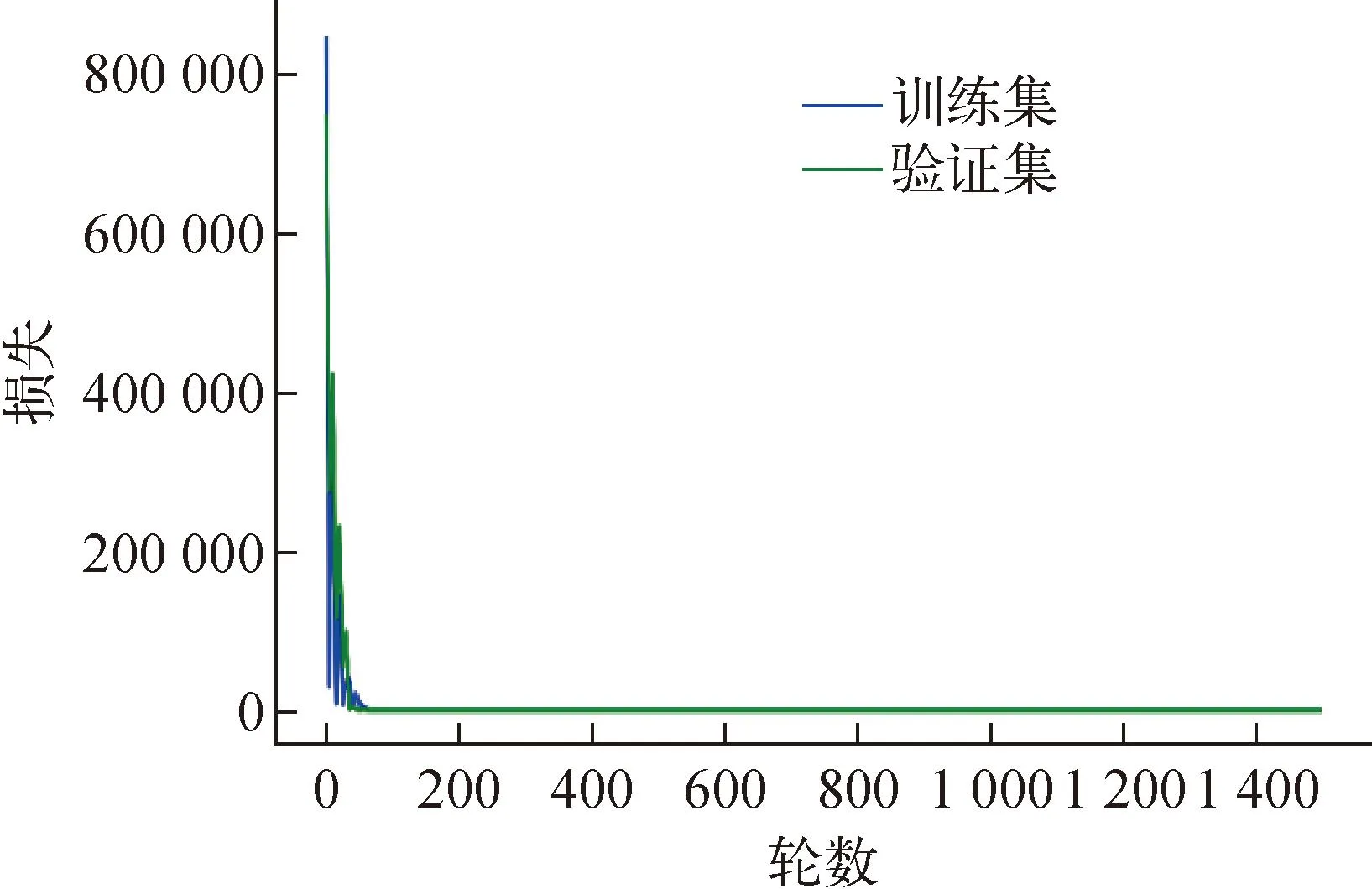
图7 训练损失与验证损失随迭代次数的变化Fig.7 Variation of training loss and validation loss with number of iterations

对神经网络结构的优化方法包括试验法、穷举法、启发式算法、修剪与构造算法等[16],其中能够自动搜索来完成的有随机配置法、系统化搜索、穷举法、启发式方法。本文使用随机配置法选取神经网络的隐藏层层数及各层节点数、学习率。4个区域各自的神经网络在初步训练后实现收敛,围绕初步训练的神经网络参数进行配置,为4个区域的隐藏层数、各层节点数、学习率设定搜索区间进行随机配置。

根据Robert Hecht Nielson的证明,1个3层的BP网络可以完成任意M维到m维的映射[17]。考虑到堆芯温度数据的输入维度远小于输出维度,将隐藏层数的选择范围设定为2～5。

隐藏层节点数的选取具有高度任意性,节点数的范围参照如下经验公式[18]并适当扩大范围:

(8)

式中:n1为隐藏层节点数;n为该层的输入神经元数;m为该层的输出神经元数;a为1～10之间的常数。节点搜索范围确定为[5,25]或[5,30]。

根据初步训练的配置,将学习率的搜索范围设为[1×10-9,1×10-7]。各区域的神经网络参数搜索范围列于表3。最大轮数设置为20 000,满足收敛条件时结束。

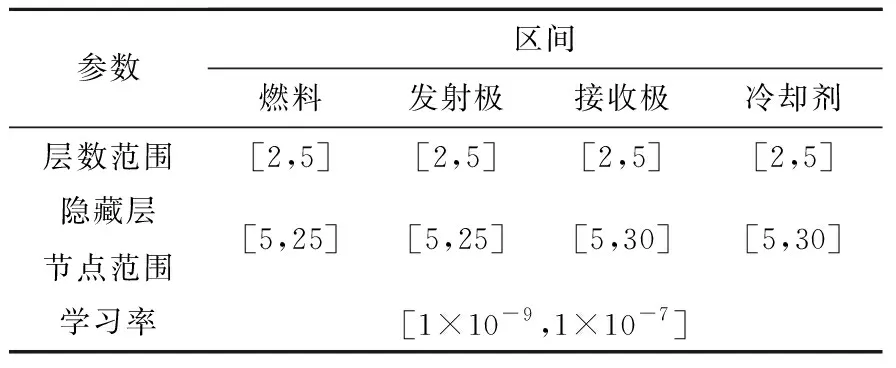
表3 不同区域的神经网络参数配置随机搜索区间Table 3 Random search interval of neural network parameter configuration for different regions

神经网络训练与优化流程如图8所示。

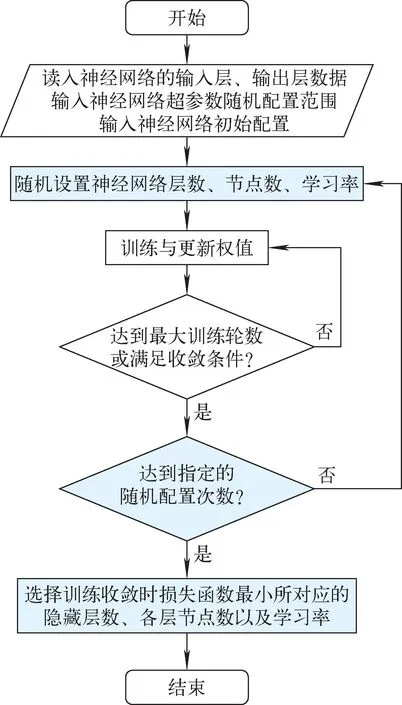
图8 神经网络训练与优化流程Fig.8 Neural network training and optimization process

对各区域分别设置30种随机组合,综合考虑训练集收敛速度最快、收敛时MSE最小的组合作为神经网络配置。当收敛轮数与最终训练损失不能同时达到最小时,选择相近的训练损失中收敛轮数最小的作为配置。以发射极为例,从30种配置结果中选出损失最小的5组,如表4所列。从中可以看出,组别为4号的配置具有最小的最终训练损失与最快的收敛速度,故作为最后的神经网络配置,训练损失变化如图9所示。

表4 发射极训练损失最小的几组配置Table 4 Several configurations of minimal training loss in emitter

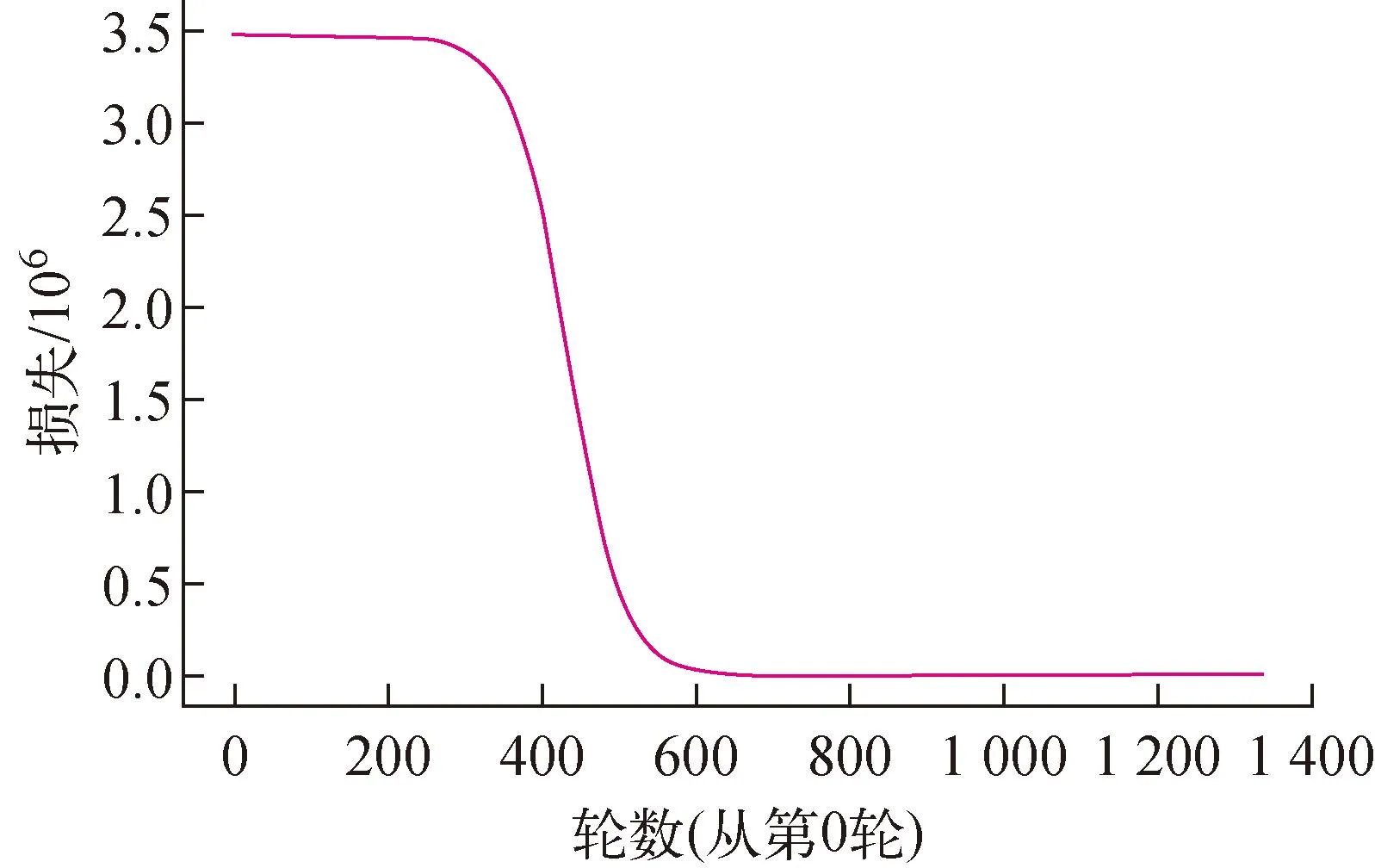
图9 发射极神经网络最终配置下的训练损失变化Fig.9 Training loss variation of emitter neural network with final configuration

通过上述流程获得4个区域的不同神经网络配置,结果列于表5。

3 反演结果

对反演值与实际数值进行比较,采用如下方式:对角线图能直观地比较反演值与实际值;相对误差频数分布直方图展示不同误差区间的数据数目;相对误差的RMSE(均方根误差)反映了反演的总体误差,计算方法为:

(9)

将上述训练好的神经网络用于15%热管失效工况下的堆芯温度数据,各部分的反演结果如下。

3.1 燃料温度反演结果

燃料温度范围在[1 370 ℃, 2 450 ℃]。燃料温度的反演值与真实值贴近直线y=x(图10),相对误差分布如图11所示。最大相对误差在±1.4%内,94.34%的数据反演值相对误差在1%以内,相对误差均方根不超过0.6%。

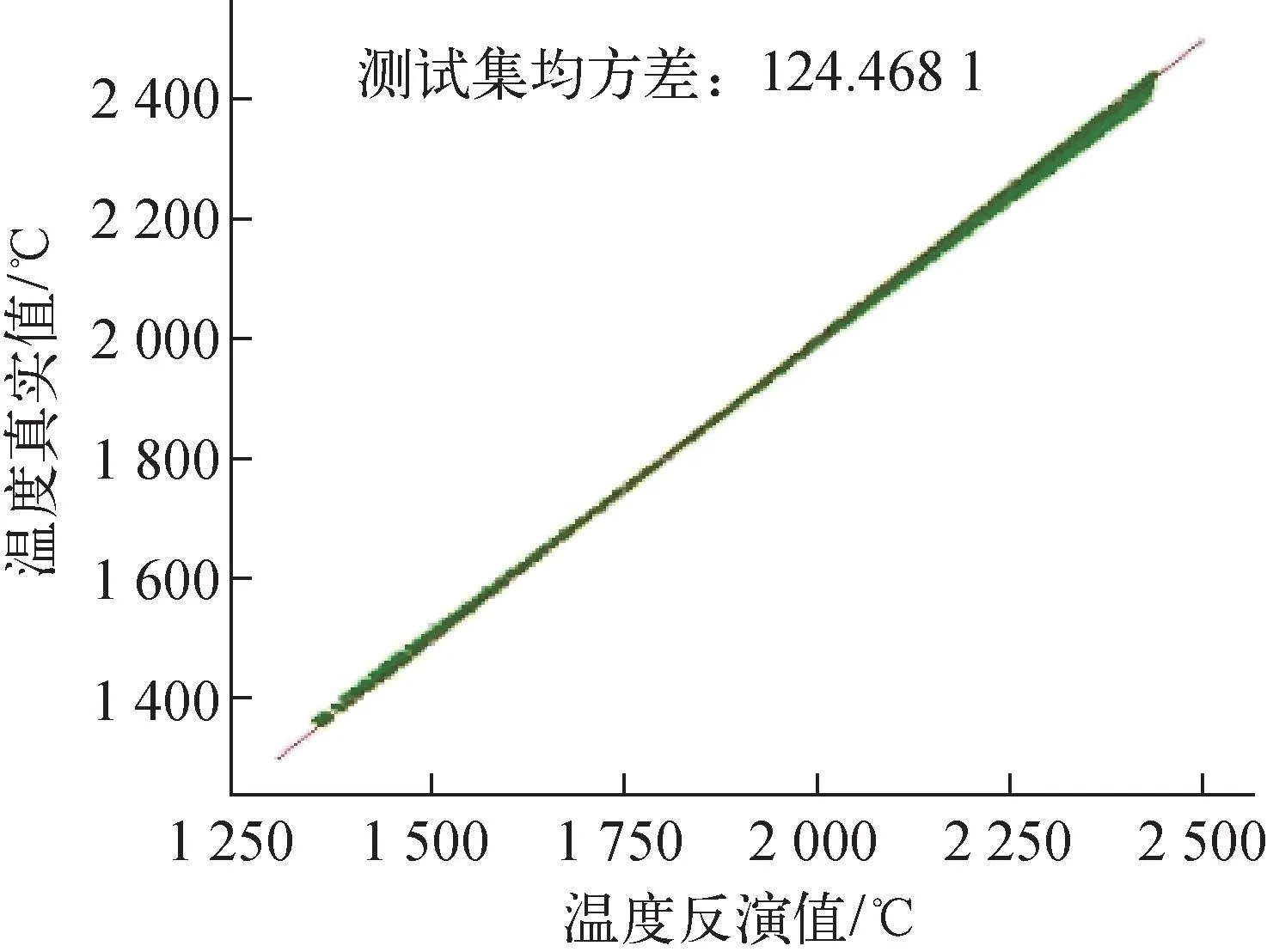
图10 燃料温度的反演值与真实值对角线图Fig.10 Diagonals of inverse and actual values of fuel temperature

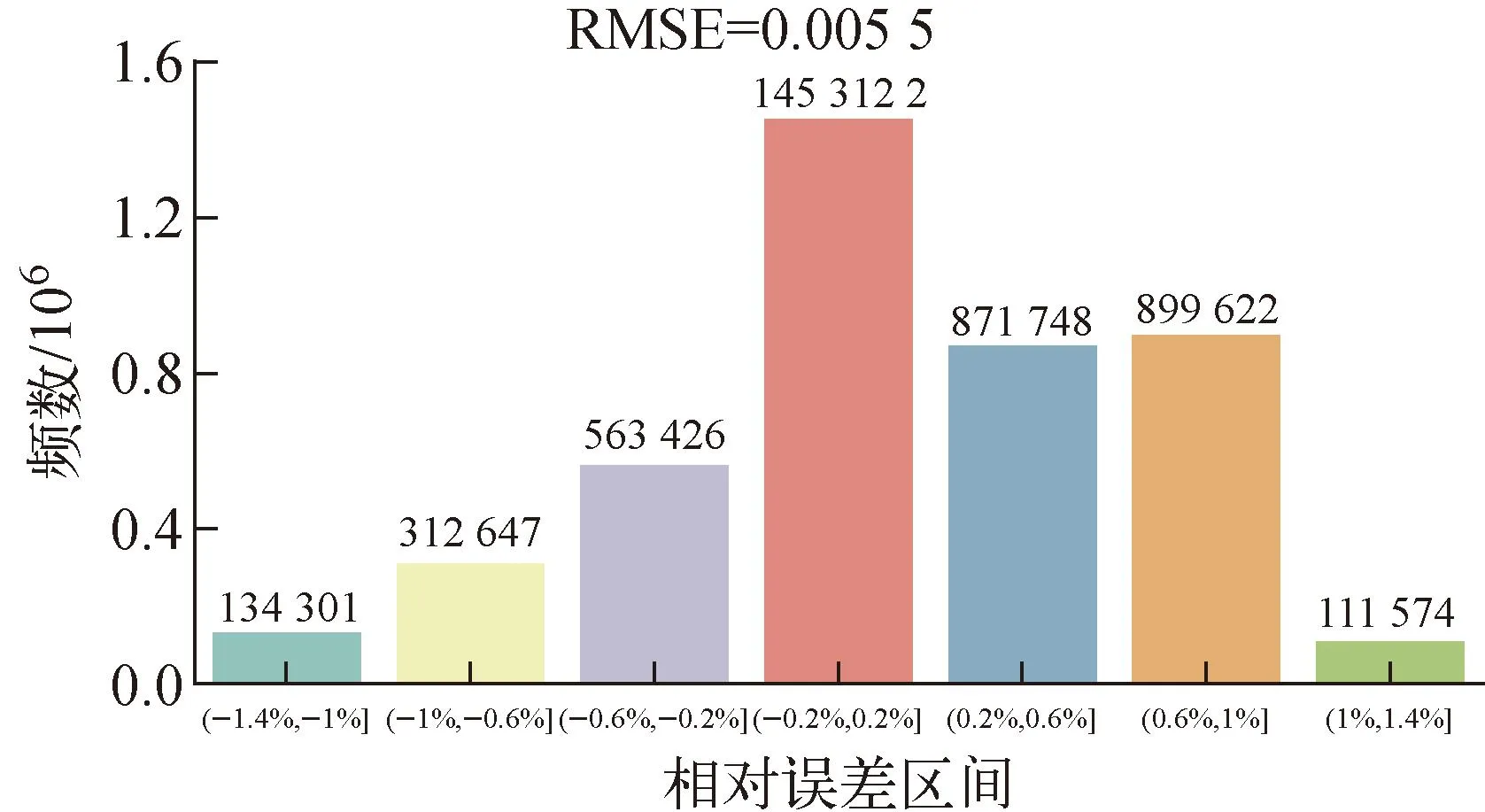
图11 燃料温度相对误差频数分布直方图Fig.11 Relative error frequency distribution histogram of fuel temperature

3.2 发射极温度反演结果

发射极温度范围在[1 350 ℃, 2 220 ℃]。发射极温度的反演值与真实值的对角线图如图12所示,相对误差分布如图13所示。最大相对误差不超过1.2%,相对误差均方根在0.4%左右。整体误差较燃料更小。

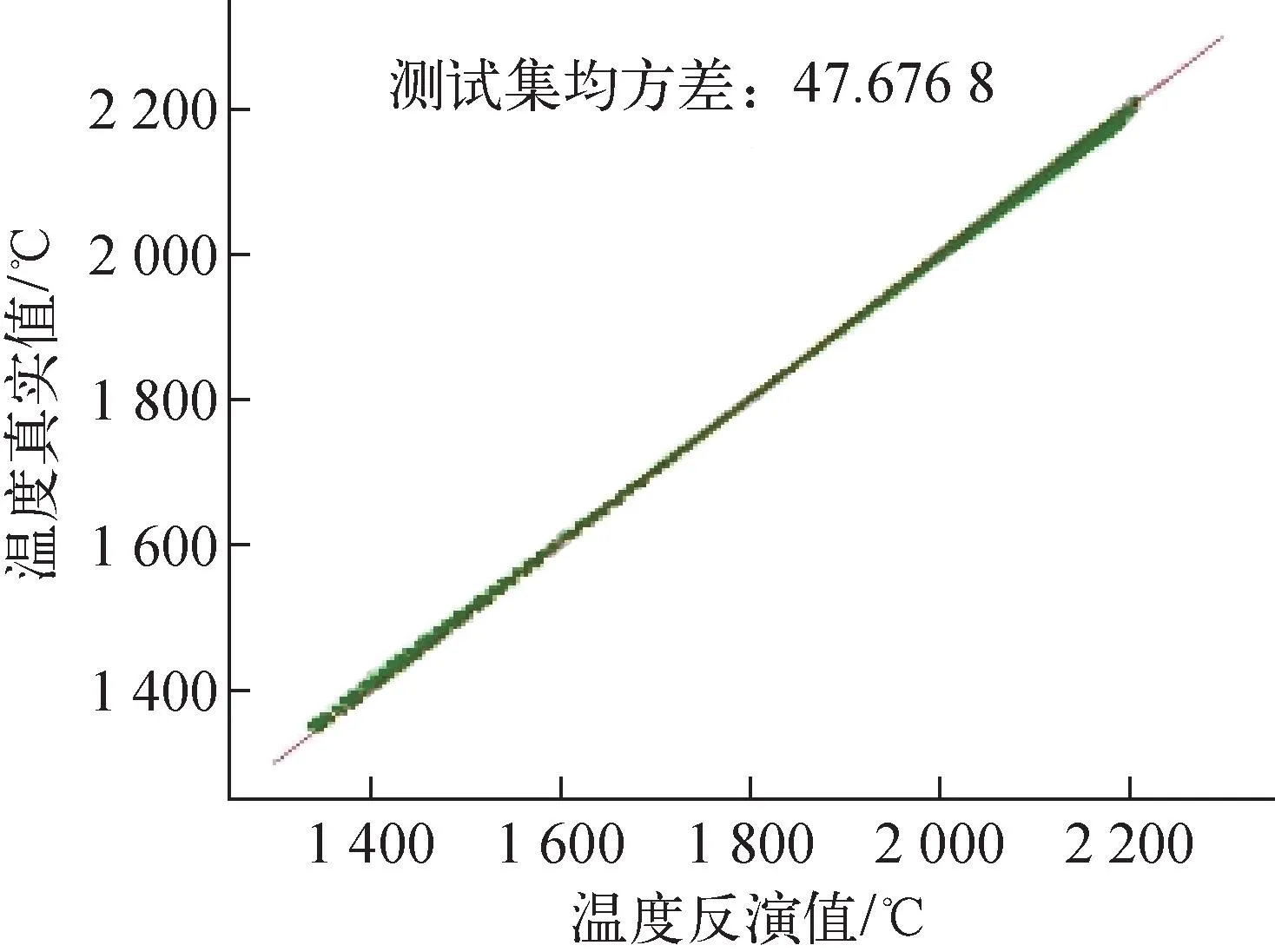
图12 发射极温度的反演值与真实值对角线图Fig.12 Diagonals of inverse and actual values of emitter temperature

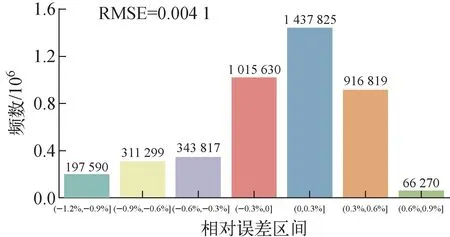
图13 发射极温度相对误差频数分布直方图Fig.13 Relative error frequency distribution histogram of emitter temperature

3.3 接收极温度反演结果

接收极温度范围在[750 ℃, 935 ℃]。接收极温度的反演值与真实值的对角线图如图14所示,误差分布如图15所示。99.75%的反演值相对误差不超过0.6%,相对误差均方根不超过0.2%。

图14 接收极温度的反演值与真实值对角线图Fig.14 Diagonals of inverse and actual values of receiving pole temperature

图15 接收极温度相对误差频数分布直方图Fig.15 Relative error frequency distribution histogram of receiving pole temperature

3.4 冷却剂温度反演结果

冷却剂温度范围在[730 ℃, 920 ℃]。冷却剂温度的反演值与真实值的对角线图如图16所示,相对误差分布如图17所示。92.09%的反演值相对误差在±0.3%以内,98.67%的反演值相对误差在[-0.3%,0.9%],相对误差均方根不超过0.2%。

图16 冷却剂温度的反演值与真实值对角线图Fig.16 Diagonals of inverse and actual values of coolant temperature

4 结论

本文在当前相关研究无法同时兼顾特征参数的自动、高效选取与保留特征参数的可解释性的情况下,基于多物理场耦合程序构建空间热离子反应堆的数字孪生,结合聚类算法与随机搜索优化的人工神经网络对20%热管失效工况下的堆芯温度建立了温度参数反演模型,并通过15%热管失效工况数据进行反演效果验证。结果表明,运用本文流程搭建的参数反演模型,对于空间热离子反应堆堆芯各区域的温度参数,反演最大相对误差在1%上下,相对误差均方根在0.001 8～0.005 5之间;能实现参数比例小于1∶10的反演,对空间热离子反应堆堆芯温度场的反演取得良好的精度,提高传输、储存与分析效率;且获取的特征参数可通过索引定位到不同构件/区域的轴向与径向位置,从而得到特征参数的物理意义。本研究的模型可以拓展应用到空间热离子反应堆其他区域以及其他堆型,高效获取特定区域的特征参数并保留特征参数的位置信息,为未来小型堆探测器的安装提供依据,也为研究大规模的核电数据提供了一种可行思路。