FAR3d程序对EAST上阿尔芬不稳定性识别过程中的应用

王曦辉,黄 娟,赵海林,J. Varela,付 静,孙延旭,史 唱,王书松

(1.中国科学院 合肥物质科学研究院,安徽 合肥 230031;2.中国科学技术大学,安徽 合肥 230026;3.Universidad Carlos Ⅲ de Madrid, 28911 Leganes, Madrid, Spain)

在未来的燃烧等离子体实验中,抑制或控制高能粒子引起的不稳定性是一个至关重要的问题。在托卡马克装置中,高能粒子主要来源于中性束注入(neutral beam injection, NBI)、离子回旋共振加热(ion cyclotron resonance heating, ICRH)等辅助加热手段,以及聚变产物之一的α粒子(3.5 MeV)[1]。由于这些粒子携带着极高的能量,且特征速度接近阿尔芬速度,因此易与等离子体背景中的阿尔芬波共振传递能量,从而激发阿尔芬不稳定性,导致快离子再分布或丢失,对装置的加热效率和安全性造成损害。因此,为有效控制高能粒子的行为,保障装置的安全稳定运行,提高聚变能源的经济性和可持续性,对于阿尔芬不稳定性的研究显得尤为重要。

尽管阿尔芬不稳定性在理论上已有较完整的物理模型,但在实际实验中,其激发和稳定性仍需进一步研究。通常情况下,阿尔芬不稳定性是根据其激发方式和不稳定特征来区分的,例如由于环效应引起的TAE[2],在安全因子极值处被激发的RSAE(reversed shear Alfven eigenmode)[3],以及由于有限比压引起的BAE(Beta-induced Alfven eigenmode)[4]等。实验中,磁探针、电子回旋辐射等诊断均可用来对不稳定性进行观测[5]。但对于不稳定性的激发机制的分析还需将诊断信息应用到具体物理模型中,所以,各种用于研究不稳定性的程序被开发出来,其中有采用完整粒子模型的GTC[6]、采用磁流体和动理学混杂模型的M3D-K[7]以及本征值程序NOVA[8]等。FAR3d是Spong、Garcia、Varela等开发的用来学习计算磁流体不稳定性和阿尔芬本征模(AE)不稳定性以及各种动理学效应对它们的影响的模拟程序[9],该程序已在国外各装置上有了广泛的应用。如在日本的仿星器装置LHD上,其被用来研究由快离子激发的TAE不稳定性的特征,模拟了快离子比压对AE不稳定性的影响[10]。在西班牙的TJ-Ⅱ仿星器装置上,研究了多种快离子不稳定性如TAE、EPM等共同存在时的特征,并通过扫描磁剪切的数值模拟,解释了实验中的TAE频率扫频现象[11]。之后,针对DⅢ-D装置中的高极向比压放电,FAR3d同样用于识别不稳定性模式,在实验可达到的参数区间内进行参数学习,提出可优化不稳定性的运行参数区间[12]。以外,FAR3d还被用来研究高能粒子对EIC(energetic-ion-driven resistive interchange mode)事件的影响[13]。

目前在全超导托卡马克装置EAST实验中,已观测到了大量的AE不稳定性现象。如中性束注入条件下激发的TAE[14],由杂质引起的撕裂模与BAE[15],磁岛和测地声模耦合引起的BAE[16]等。本文针对EAST高βN运行模式条件下观察到的AE不稳定性,首次将FAR3d程序应用到EAST上,并结合相关扰动测量进行验证以及细致分析,为进一步不稳定性产生机制的研究和有效控制提供物理依据。

1 实验研究

1.1 EAST及快离子不稳定性诊断

EAST装置为全超导托卡马克装置,大半径R=1.85 m,小半径a=0.45 m。EAST装置的位型与ITER类似,均为非对称的偏滤器位型。在EAST实验中,快离子主要由ICRH和NBI加热产生。目前,EAST上的NBI加热系统拥有两条束线,可稳定地在65 keV束压条件下提供共计5 MW以上的功率[17]。离子回旋系统目前拥有两条天线,可稳定提供2.5 MW以上的输出功率[18]。

在快离子不稳定性的诊断方面,EAST装置上配备了最高可探测到500 kHz频率的高频磁探针,来测量不稳定性造成的高频磁扰动,并通过磁探针在环向空间上的分布可以计算得到不稳定性的环向模数。EAST上的电子回旋辐射诊断则可以通过测量不稳定性造成的电子回旋辐射扰动,借由其多道外差系统,来提供厘米量级的空间分辨和微秒量级的时间分辨,给出不稳定性的位置和频率信息。除此以外,EAST中还配有软X射线诊断、束发射光谱诊断等对快离子不稳定性进行测量。在上述的不稳定性的直接测量手段以外,EAST中还配有多种诊断来提供快离子的信息。其中,快离子损失探针可以测量不稳定性引起的快离子损失,以及FIDA(fast ion D-Alpha)诊断可以反演得到快离子的速度空间分布函数。本文中主要使用了高频磁探针诊断和电子回旋辐射诊断,基于测到的不稳定性的模数、频率、位置等信息在实验上对不稳定性做初步分析。

1.2 实验条件

93910炮放电的纵场Bt为1.6 T,等离子体电流Ip=400 kA,电子密度平台大约在2.5×1019m-3,在t=6.5 s时刻,q95=4.0,βN=1.8,有效电荷数Zeff=2.5。该放电使用了总功率为1 MW的低杂波加热和总功率为5 MW的NBI注入加热。具体放电参数演化如图1所示。图1e为所选时间范围内的高频磁探针诊断的频谱图,可看到在t=6.0 s后,磁探针信号出现了较大的扰动,多支不稳定性已被激发。为避免多个模式的干扰以及诊断测量的时间分辨限制,本文选择了该次放电t=6.5 s的时刻点来进行分析,此时具有扫频特性的不稳定性已消失,仅剩一支90 kHz附近的频率较稳定的模式。

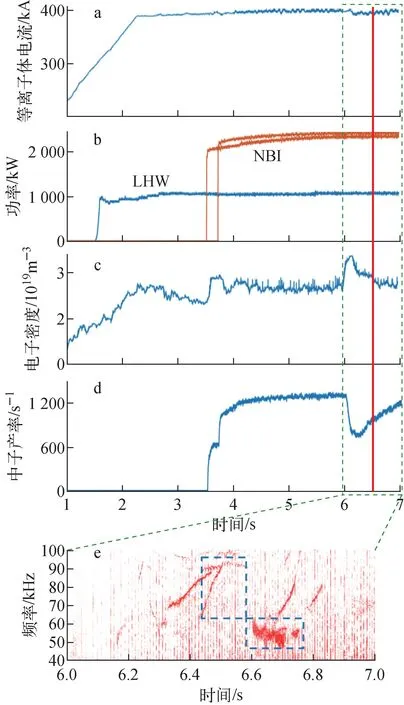
a——等离子体电流;b——辅助加热,蓝色线为4.6 GHz低杂波,橙色为两条NBI束线;c——电子密度;d——中子产率;e——6～7 s时的高频磁探针频谱图1 93910炮放电基本参数Fig.1 Basic parameters of shot 93910

2 FAR3d模拟程序简介

2.1 程序概述和物理模型

FAR3d程序是由Spong、Garcia、Varela等开发的一用来学习研究线性MHD和AE不稳定性的模拟工具[19-20]。FAR3d采用gyro-fluid模型,通过求解一系列的简化的线性电阻MHD方程组[21],并在其中添加了快离子密度和平行方向的动量的变化,把与快离子相关的效应加入到了程序的物理模型中。如通过加入线性的波-粒共振引入朗道阻尼,加入热离子平行动量的响应耦合测地声模对不稳定性的影响[22]。

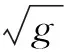
(1)

(2)

(3)

(4)

FAR3d程序中将等离子体的热成分和快成分分为两部分。其中热成分可写为:

(5)

(6)

(7)

(8)

以涡量方程(式(6))为例,介绍模型中所考虑的效应。式(6)中第1项表示的是平衡的环向旋转带来的影响;第2、3项为电流在磁场B方向的变化的影响;第4项为等离子体压强梯度项;第5项为快离子的密度梯度驱动项;第6项为热离子的有限拉莫半径效应项;第7项为朗道阻尼项;第8项表示双流体效应影响。此外,式(7)中第3、4项表示声波带来的压缩效应。FAR3d模型中,通过引入快离子密度和平行方向的动量的变化,把与快离子相关的效应加入到了程序的物理模型中。描述快离子成分的关系式如下。

(9)

(10)

目前FAR3d模型中对于快离子部分的处理,仅引入了高能粒子的平行速度的变化,对平行能量较高的粒子引起的不稳定性有较好的模拟效果,而对于快离子垂直方向的运动引起的不稳定性的模拟,还需后续版本的继续升级来获得更合理的结果。

2.2 程序输入与输出

FAR3d程序的输入由3部分组成:平衡文件;输入参数表单,其中主要包含各种效应的开关选项;还有就是等离子体的宏观参数剖面,如热离子的密度、温度、快离子的密度剖面等。FAR3d现在仅支持VMEC格式的平衡文件输入,目前EAST上使用的是EFIT的平衡[25],在使用FAR3d程序的过程中,需将EFIT平衡转换为VMEC平衡再作输入[26]。针对93910炮放电,本文中使用了EFIT、ONETWO/NUBEAM程序来对t=6.5 s时刻进行动理学反演,得到EFIT格式的平衡输入文件。

进行动理学平衡反演的过程以及EAST装置中的诊断可提供绝大多数FAR3d程序所需要的输入参数剖面。图2示出了诊断测量参数拟合过后的结果,即FAR3d中的输入剖面。其中包括汤姆逊散射(TS, Thomson scattering)和偏振干涉仪诊断(POINT, polarimeter-interferometer)提供的电子温度Te和密度ne剖面,电荷交换复合光谱(CXRS, charge exchange recombination spectroscopy)提供的离子温度Ti剖面。在ONETWO/NUBEAM输出中可得到快离子部分的能量Tf以及密度nf剖面。

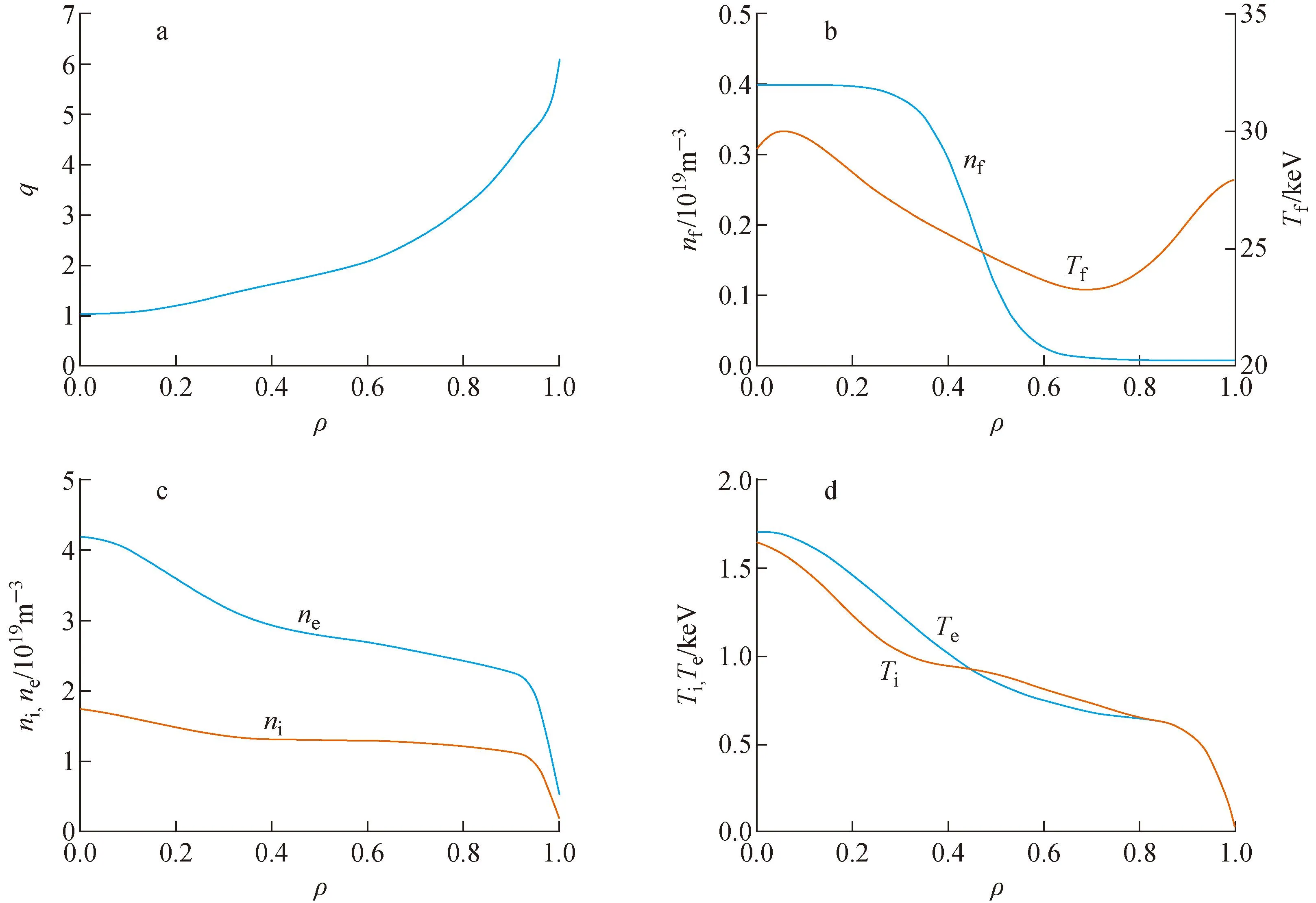
a——安全因子剖面;b——快离子温度与密度剖面;c——电子与离子密度剖面;d——电子与离子温度剖面图2 FAR3d模拟中的输入参数剖面Fig.2 FAR3d input profiles

目前,FAR3d程序有两种运行模式,一种是initial value solver,尽管在FAR3d程序中该模式运算速度很快,但对每步计算只能给出一个最不稳定模式的信息。另一种运行模式是eigensolver,该模式可计算出给定频率/增长率范围内的所有的可能为不稳定的模式,且包括其计算出的所有模式的本征函数,而不仅只有增长率最高的主导模式。由于本文中所选择的放电存在多种不稳定性,所以本文所有结果均由eigensolver模式产出。在eigensolver模式下,程序可给出其发现的所有不稳定性的频率、增长率以及模结构,从中可得到各模式的环向和极向模数。

2.3 AE不稳定性分析

1) 实验特征

如图1e所示,在t=6.0～6.5 s之间,磁探针探测到强烈的不稳定性现象,且具有随时间向上扫频的特性,频率范围为70～100 kHz,且还有一支约90 kHz的模式几乎保持频率不变。t=6.6 s开始,在50～60 kHz左右的较低频率区域也出现了频率范围较宽的不稳定现象,随时间频率略微降低。同时伴随着一频率较高但强度较弱的向上扫频的模式。

通过EAST中的高频磁探针在环向上的阵列,计算出各点信号的相位差即可得到不稳定性的环向模数信息,如图3a所示,两支模式的环向模数均为n=1～2。结合图3b所示的ECE外差系统的观测结果,可得t=6.3 s时刻开始出现的频率从70 kHz上升至100 kHz的模式,其环向模数为n=2,径向位置在ρ=0.46。另一个在t=6.6 s时刻出现的60 kHz附近的模式同样在径向上位于ρ=0.46附近。需注意的是,该次放电为低纵场放电,电子回旋辐射基频较低,ECE诊断测到的电子回旋辐射信号已经处于3次谐频范围,所以其信号较弱。且该次放电的环向磁探针阵列仅有两个高频磁探针可用,所以对于环向模数的计算可能会有一定的误差。在下一小节中,通过FAR3d程序对t=6.5 s时刻的不稳定性做线性模拟分析。

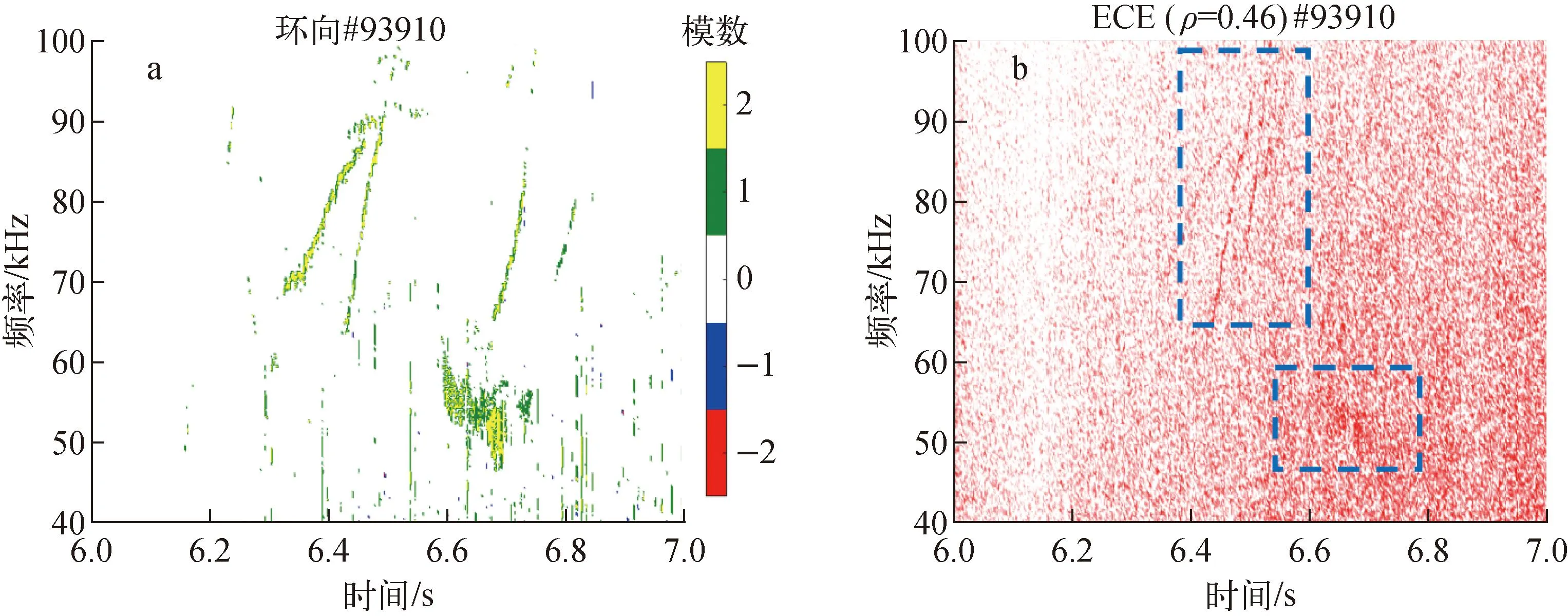
a——环向磁探针阵列;b——ECE诊断测量图3 不稳定性的环向模数与位置Fig.3 Toroidal mode number and radial location of instability

2) FAR3d程序的模拟结果

FAR3d模拟显示只有n=2的模式是不稳定的。图4为FAR3d在eigensolver运行模式下的模拟输出结果,增长率按阿尔芬时间进行了归一。其中红色方框处为增长率最高的主导模式,频率为87 kHz,蓝色方框处为次级主导模式,频率为62 kHz。图5为主导模式和次级主导模式静电势的本征函数。从图5a可看出,主导模式本征函数较宽,由n/m=2/3和n/m=2/4的模式耦合而成,位置在归一化半径ρ=0.45附近,这与实验观测结果是一致的。图5b展示了频率为62 kHz次级主导模式,其本征函数非常窄,是由单一的极向模式所组成,其模数为n/m=2/4,位置在ρ=0.55附近。

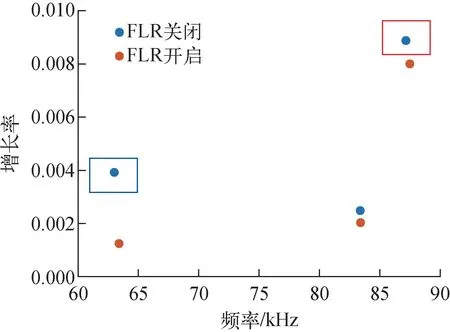
图4 开启/关闭FLR效应时FAR3d的模拟结果的增长率与频率信息Fig.4 Modes’ growth rate and frequency of FAR3d results with/without FLR effect activated

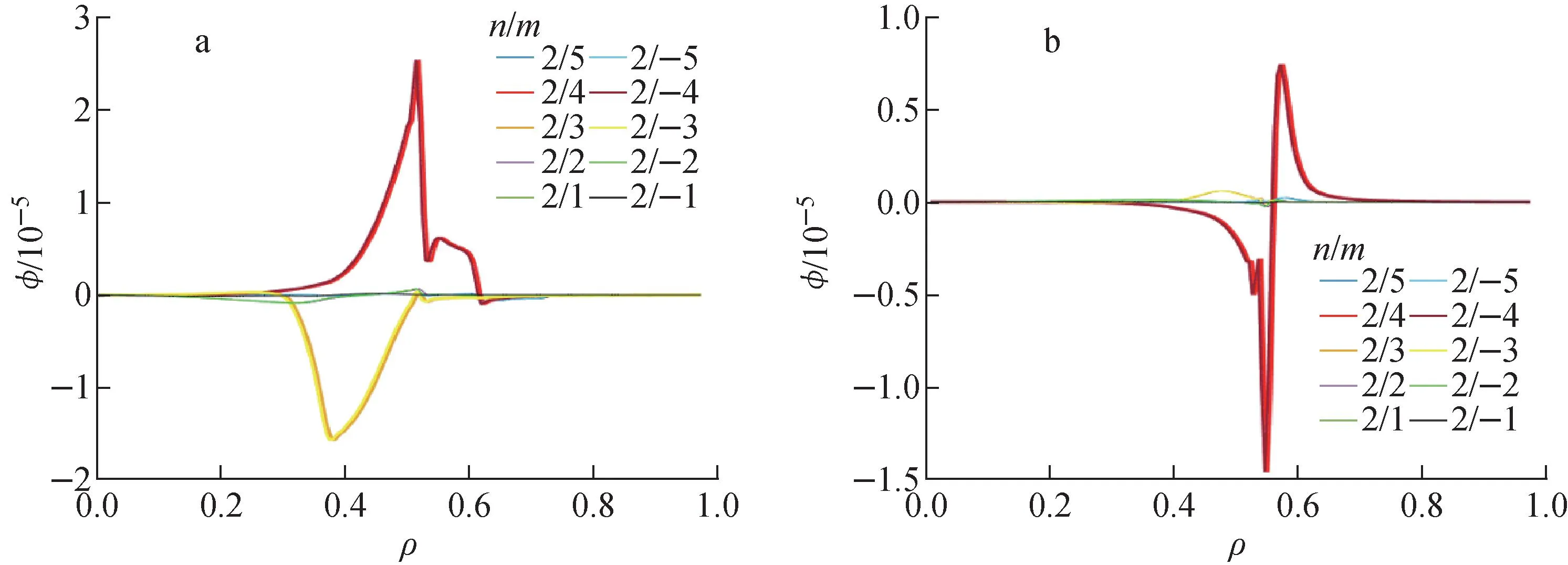
a——主导模式(图4中红色方框);b——次级主导模式(图4中蓝色方框)图5 主导模式和次级主导模式的本征函数Fig.5 Eigen functions of dominant and subdominant modes

为进一步确定各模式的信息,本文使用StellGap程序计算出图6中的阿尔芬连续谱[27]。图中红色横线表示主导模式的位置,蓝色横线表示次级主导模式所处的位置。从中可看出,主导模式位于谱间隙的底部,而次级主导模式则位于连续谱内。因此可判断,主导模式为n/m=2/3,2/4的TAE,频率为87 kHz,次级主导模式则为n/m=2/4的EPM。需注意,连续谱中的主导模式和连续谱线有少量的重叠,这是由于StellGap程序与FAR3d中对于声波的耦合方法不同所导致的。在图5a中2/4尖锐的模结构则是由于模拟中未开启FLR效应,因此FAR3d程序会计算出此处存在一较窄的模结构并且与当前模式混合。如图7所示,在FLR效应带来的阻尼下,不稳定性中较窄的模结构已消失。同时也可看出,该模式并不是位于连续谱中的模式。至此,FAR3d模拟成功得到了与实验观测一致的不稳定性且识别了主导模式为TAE和次级主导模式为EPM的不稳定性。模拟使用的宏观参数剖面以及平衡均为t=6.5 s时刻,但在实验观测中60 kHz附近的低频模式直到t=6.6 s才出现,而且本文的模拟中并未进行非线性模拟分析,所以对于模拟中得到的次级模式EPM是如何演化并成为主导模式的,还需后续进一步分析。

图6 t=6.5 s时刻的阿尔芬连续谱以及不稳定性所处的位置Fig.6 Alfven continuum and location of instability at t=6.5 s

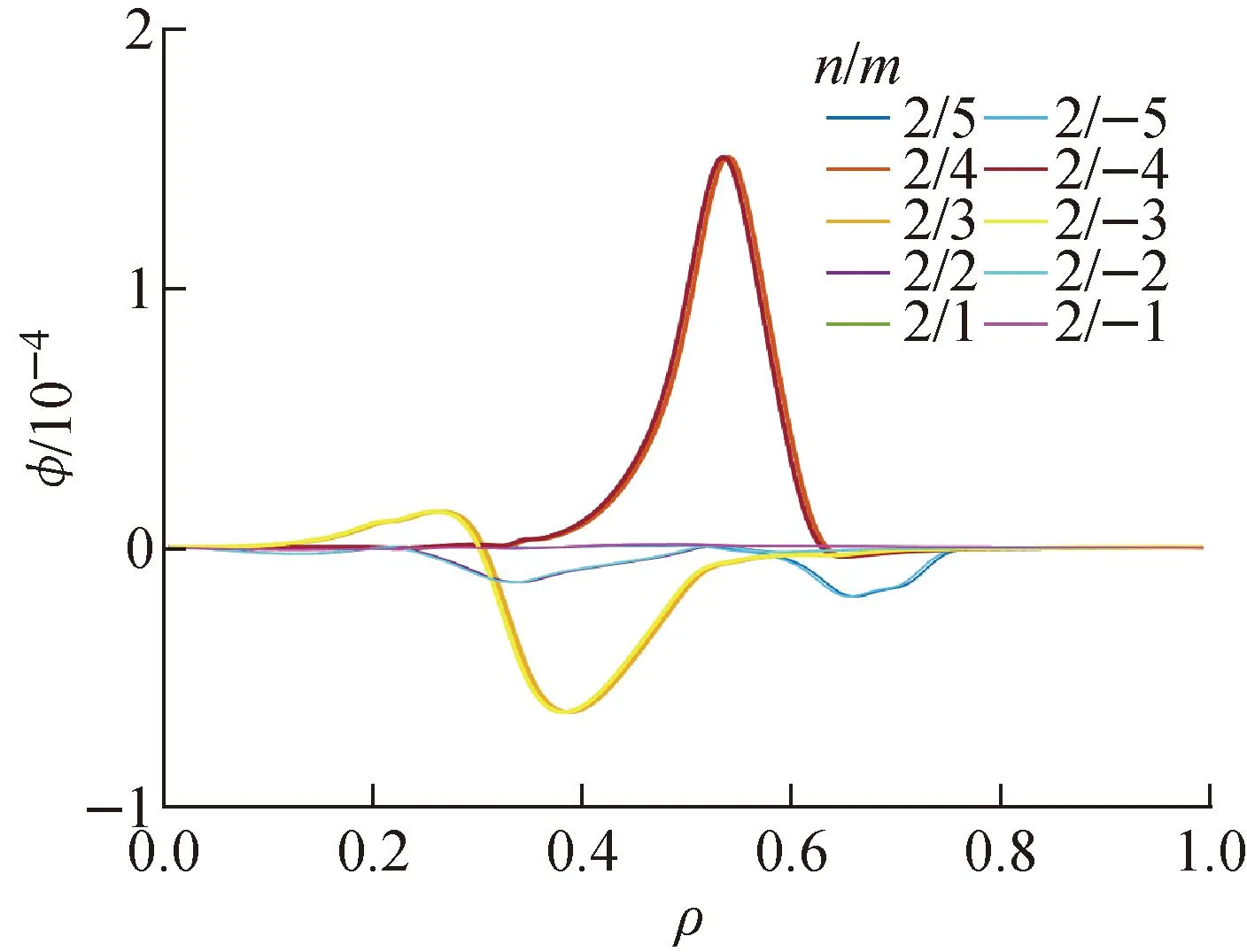
图7 开启FLR效应后的主导模式的本征函数Fig.7 Eigen function of dominant mode with FLR effect included

需要提到的是,即使FAR3d模拟中会计算出多种不稳定模式,但由于驱动源所能提供的自由能量的限制,若多种模式均由同一种源来获得能量,如某处的快离子压强梯度,那么在自由能获取的竞争中,通常增长率最高的主导模式会在竞争中胜出从而有最大的可能表现在实验中。对于不稳定性从出现到各自的模式演化过程,想要得到模式更准确的信息,还需要后续再进行进一步的非线性模拟分析。除此以外,由于FAR3d模拟程序仅从数值上得到收敛的结果,因此程序可能会计算出一些仅从计算上合理但无实际物理意义的“人造”解。所以,对于程序的计算结果,需要加入合理的物理理解,来排除干扰,解释正确的物理现象。

在识别EAST等离子体中的不稳定性模式时,并不需将所有的动理学效应项目均加入到计算中,可根据放电参数的不同,先使用FAR3d程序中各个动理学项对不稳定性模式的影响进行简单的评估,再考虑是否需要将这些项加入到计算中。以有限拉莫半径效应为例,在图4可看到,在93910炮放电中,开启有限拉莫半径效应后,等离子体的不稳定性在增长率上仅有微小的差别,对于模式的识别并没有影响。这是因为FLR效应对于低n模式影响较小,而对于高n模数的模式影响较大。因此,在93910炮的计算中,选择关闭有限拉莫半径效应,以使计算更加快速。而对于高n的模式,FLR效应则可能会带来强烈的阻尼效应。

3 总结与展望

针对EAST高βN运行区间观测到的快离子相关不稳定性,在EAST上应用FAR3d程序,并结合快离子不稳定性诊断测量进行相关验证和分析。基于93910炮放电,t=6.5 s的时刻点进行线性模拟分析,成功重复出了实验中出现的不稳定性模式,且判断为m/n=3/2、4/2的TAE以及m/n=4/2的EPM,频率与位置信息均与实验测量结果吻合。成功将FAR3d程序应用到了EAST装置中。并且评估了低n模数的AE不稳定性,有限拉莫轨道半径效应对不稳定性的影响较弱。在实验中,与磁探针提供的不稳定性环向模数结合,适时的关闭该效应有利于提高计算速度。本文仅讨论了t=6.5 s时刻的AE不稳定性。对于不稳定性的扫频现象,以及其激发机理的研究,后续会进行进一步的模拟分析。在未来实验中,将结合ICRF和NBI协同加热产生的快离子激发的相关不稳定性进行深入分析,同时进一步发展FAR3d程序相应的物理模型,对快离子不稳定性的有效控制提供实验依据和指导。