基于XFEM 的大体积结构波动传播规律及裂纹反演方法
卢皓卓 江守燕
(河海大学 工程力学系, 南京 211100)
大体积混凝土结构被广泛应用于土木、水利等基础设施中,而混凝土抗拉强度低的力学特性决定了其极易产生裂纹,裂纹是降低混凝土安全性的主要病害,因此对混凝土进行裂纹检测十分必要.无损检测方法是在不破坏待测结构自身的情况下,利用仪器对结构缺陷进行原位检测,从而判断缺陷的位置、形状与尺寸等特征,为分析与评估结构的安全性提供依据.基于波传播规律的混凝土裂纹无损检测方法已经得到广泛应用,按照波的类型主要可以分为基于表面波(瑞利波)的检测方法[1-3]、基于剪切波(SH、SV 波)的检测方法[4-6]等.
随着人工智能技术的发展,数值仿真模拟与智能算法相结合的裂纹检测方法是近年来研究方向之一.在数值模型方面,扩展有限元法(extended finite element methods,XFEM)[7]在裂纹形态演化时无需重划分网格,是含裂纹体结构建模的常用工具[8-10];通过与各种人工吸收边界的结合[11-13]可在减小模型求解域的同时,消除模型边界反射波对模拟结果的干扰.在智能算法方面,Jung等[14]提出了一种基于梯度的优化算法,对XFEM 裂纹模型波动响应进行反演;Rabinovich等[15]提出了基于XFEM 对含裂纹模型大量样本进行正演,再通过遗传算法进行反演的方法;王佳萍等[16]在此基础上进行了进一步研究;Sun等[17]提出了一种自适应的增强人工蜂群反演算法,与XFEM 建模正演相结合;在此基础上,沈学港等[18]进行了进一步研究,提出了一种多缺陷三步反演方法;Jiang等[19]提出了将机器学习与XFEM 相结合,采用极限学习机算法训练神经网络,以实现多缺陷反演.相比而言,人工神经网络模型能更高效地处理正演数据特征,获得较准确的反演结果,被较多学者关注[20-23].
本文提出了一种基于波动响应的频域特征和BP神经网络的裂纹反演模型.分别对单裂纹和双裂纹情形,采用数值模拟方法,通过在检测域内产生大量裂尖位置坐标,计算、提取特定位置传感器在每个裂尖位置下的响应信号,提取特定频率范围内的幅值数据,产生一个包含大量样本的频域特征—裂尖坐标数据集,以供神经网络进行训练,从而建立裂纹反演数据模型.在实际应用中,只需输入传感器的响应信号,便可输出裂尖坐标.
1 扩展有限元法
1.1 XFEM 位移模式
XFEM 通过在常规有限元的位移模式上引入具有不连续性质的改进函数来实现对不连续问题的表征.对于裂纹问题,采用两个改进函数,即Heaviside改进函数H(x)和裂尖改进函数G l(x):
式中:x为考察点的位置坐标;x*为考察点在裂纹面上投影点的位置坐标:n为裂纹面在x*处的外法线方向的单位向量.
式中:r,θ为裂尖局部极坐标系中的位置坐标.
采用水平集法,可以确定裂纹与单元的位置关系,进而把单元分为二类(具体方法可参阅文献[24]):一是Heaviside改进单元,其节点组成的集合记为S1,应用改进函数H(x);二是裂尖改进单元,其节点组成的集合记为S2,应用改进函数G l(x).进而,XFEM 位移模式可以表示为:
式中:N i(x)为第i个节点在常规有限元法中的插值形函数;N*i(x)为第i个节点对应的单位分解函数,通常取为与N i(x)相同的形式;u i为第i个节点在常规有限元法中的位移;v i为第i个第一类改进节点的位移;w il为相关的第二类改进节点的位移;S0为有限元模型求解区域内所有节点的集合.
1.2 XFEM 控制方程
按照上述位移模式,运用虚功原理,得到XFEM的控制方程为:
式中:K ij为整体刚度矩阵;C ij为整体阻尼矩阵;M ij为 整 体 质 量 矩 阵(i,j=u,v,w);x,分 别 为 节 点位移、速度、加速度列阵(x={u,v,w});F i为节点荷载列阵(i=u,v,w).
2 多向吸收边界模型
对大体积结构进行波动响应模拟时,若选择对整个结构进行完全模拟,将需要很大的计算量.一般情况下,裂纹扩展的尺寸远远小于结构的尺寸,故可以考虑取裂纹附近的一定区域作为模拟域以减小计算成本.但此方案同时会带来应力波在区域边界上反射,进而需要在模拟区域边界加以一定厚度的反射层.按照文献[12],采用一种基于瑞利阻尼的多向吸收边界层方法.该模型通过对吸收边界层中不同位置加不同的阻尼比来实现,表达式为:
式中:α为控制衰减的系数;x为考察点的位置坐标;xΓ为吸收层外边界上一点的位置坐标;ξ0为吸收层厚度,为吸收层外边缘的阻尼比.即该模型中,阻尼比在吸收边界层的外边缘处为最大值ξ0,沿厚度方向呈指数衰减,在吸收边界层与检测域交界的内边缘处为最小值ξ0e-α.
瑞利比例阻尼方法将阻尼矩阵表示为质量矩阵和刚度矩阵的线性组合:
式中:C为阻尼矩阵;M为质量矩阵;K为刚度矩阵;a1、a2为瑞利阻尼系数,与阻尼比的关系为:
考虑在两个波动频率f1、f2的情形下,确定瑞利阻尼系数a1、a2,使得两个波动频率下的阻尼比均为ξ,方程如下:
解出a1、a2,并写成关于坐标的函数形式:
结合式(5),即得到边界层中一点的瑞利阻尼系数关于位置坐标的函数关系.
3 BP神经网络模型
机器学习是一种通过输入包含大量样本的数据集,自动改进计算机程序算法或参数的方法.即使当数据之间的关系复杂,难以使用数学表达式显式描述时,机器学习仍能够应用于建立输入数据与输出数据之间的关系.例如分类、拟合或聚类等.人工神经网络是一种类似于人类大脑结构和神经系统工作原理的机器学习方法.神经网络中的每一个节点都可以通过多个输入信号通过函数运算得到一个输出信号.神经网络通常采用多层结构,每层中节点的输出与下一层中节点的输入相连.
神经网络节点对输入数据的处理包括加权、偏置和激活,输出值的表达式为:
式中:w为权值列阵;x为输入值列阵;b为偏置值;φ(*)为激活函数.φ(*)的常用形式包括Sigmoid函数:
双曲正切函数:
修正线性单元函数:
激活函数使得传播过程具有非线性特征,网络为多层时,神经网络能够处理高度非线性问题.
经过正向传播后,为了评价输出值与实际值的差距,需要定义损失函数,较为常用的损失函数为平均平方误差函数:
式中:x i为第个预测值;x*i为第个真实值;n为一次优化的输出值个数.
反向传播用于调整每个神经元的权重值列阵和偏置值.常用的方法是梯度下降算法,其迭代格式为:
式中:W为所有可训练参数的列阵;β为学习率;当网络为多层时;∂L/∂W i的值需由链式求导法则确定.
4 数值模型
选择二维模型进行模拟,原结构模型为长24 m,高12 m 的矩形;模拟域几何模型为长4.0 m,高1.6 m的矩形.混凝土按照各向同性材料建模,弹性参数为:弹性模量E取30 GPa,泊松比υ取0.2,质量密度ρ取2 500 kg/m3.将模型上边界中点设定为坐标原点,激励信号源位于(-1.0 m,0.0 m),大尺寸原结构模型、模拟域包含单裂纹和双裂纹的模型示意如图1所示.
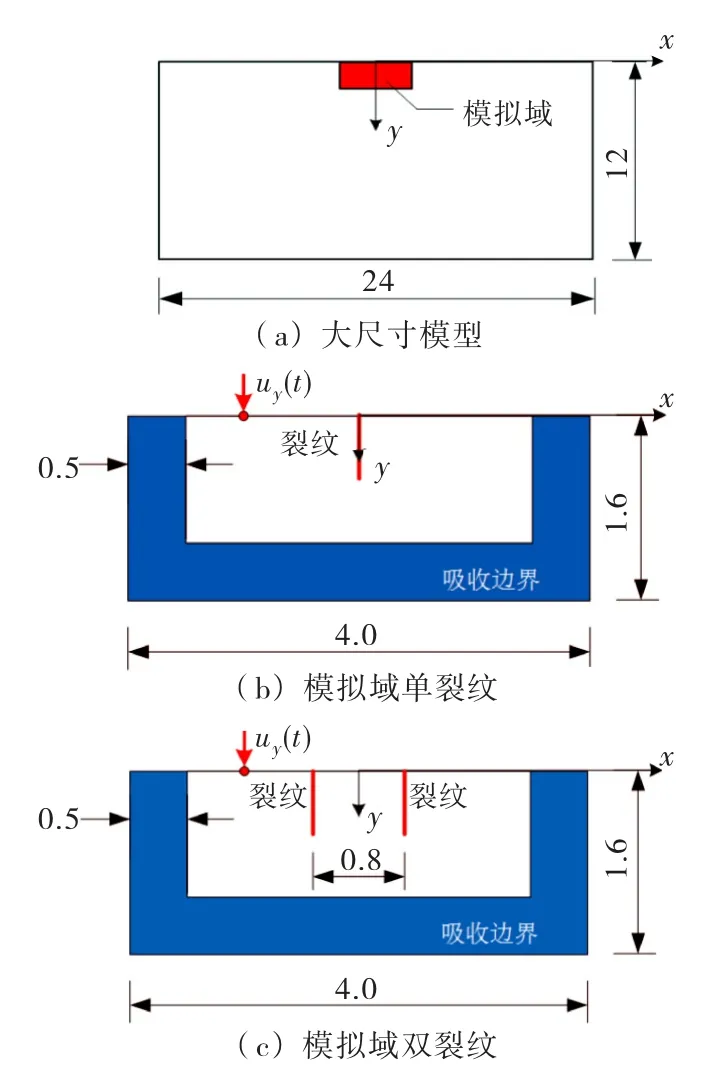
图1 几何模型(单位:m)
压缩波速和剪切波速按照下式计算:
计算出剪切波速为2 236 m/s,压缩波速为3 651 m/s.信号的两个主频f1、f2分别选取为相同波长的压缩波频率fp和剪切波频率fs.波长λ取为0.5 m,由f i=c i/λi,计算出f1=fp=7 302 Hz,f2=fs=4 472 Hz.信号波形取为等振幅的两主频正弦波叠加后,经汉宁窗处理后得到的波形,表达式为:
式中:Hw(*)为汉宁窗函数,其表达式为:
式中:τ为窗口宽度,取2×10-3s;而A(t)为两主频的正弦波的叠加,表达式为:
式中:A0为正弦波的振幅,取为10μm,激励信号波形如图2所示.
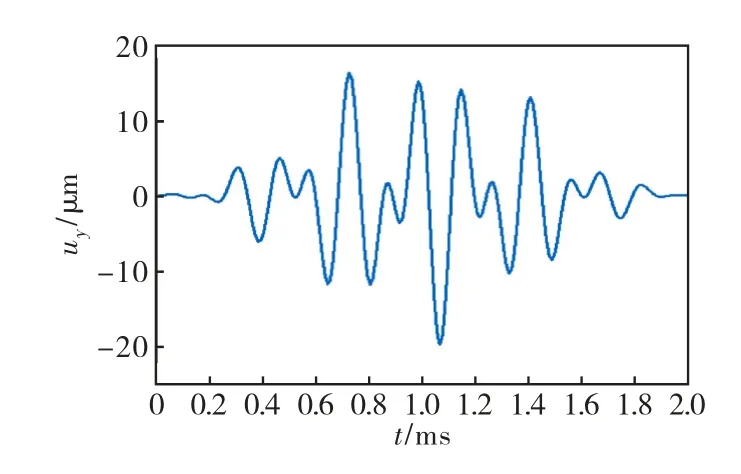
图2 激励信号
采用四边形线性等参单元,单元边长取为波长的1/10,即0.05 m.由于采用XFEM 网格无需沿裂纹布置,可以采用结构化网格划分方式以提高网格质量.整个模型共2560个单元,共2 673个结点,网格如图3所示.

图3 单裂纹情形下传感器布置
为达到充分吸收效果,吸收边界厚度取为与波长相等[12],即0.5 m.对于吸收边界区域内每个单元,取单元形心位置坐标x代入式(9)确定单元瑞利阻尼系数.经试模拟计算,式(5)中取时具有较好的吸收效果.为提高数值模拟精度,时间步长取为波动周期f-1的1/50,这里取为2.5μs.为使响应输出点获得较完整的时域响应,总时间取为6 ms.由于裂缝以XFEM 定义,改变裂尖位置无需对混凝土模型进行修改.对于单裂纹情形,共设置357种不同裂尖位置;对于双裂纹情形,共设置750种不同裂尖位置组合.
5 响应分析
以单裂纹情形为例,分析不同传感器位置和不同裂尖位置下的响应.在裂纹右侧布置两个传感器:位于(1.0 m,0)即与信号源关于裂纹开口处对称的传感器1、位于(0.1 m,0),即紧邻裂纹的传感器2,如图3所示.
传感器用于输出y方向上的振动响应,对时域响应进行快速傅里叶变换,并求各频率的幅值,得到频谱曲线.为验证多向吸收边界的吸收效果,取裂尖位置不变,比较图1(b)所示模拟域、未设置吸收边界的模拟域、图1(a)所示大尺寸完整模型的模拟结果,3种模型中传感器1接收响应的频谱曲线如图4所示.
不难发现,设置了吸收边界的小尺寸模拟域与大尺寸模型中实际响应相近,频谱曲线基本重合;而未设置吸收边界的模型由于反射波的干扰,幅值明显偏大.说明该多向吸收边界模型效果较好,在减小模拟域的同时,消除了边界反射波的干扰.
传感器1在裂尖横坐标x=-0.10 m 不变,不同深度y下5条频谱曲线、深度y=0.45 m 不变,不同横坐标x下5条频谱曲线如图5所示.
可以发现,频谱曲线具有较明显的4个峰值,分别所处的频率范围见表1.其中,频段3、4为输入信号的两主频,频段1、2 是由传播过程中的频散造成的.不难发现,频段3幅值具有随深度增加而单调减小的特点,而对x不敏感;频段4幅值明显且呈现出随|x|的增大而降低的规律,而对x的符号不敏感;频段2幅值随x增大(裂尖向右移动)而略有升高.

表1 频谱曲线各段频率范围
传感器1在裂尖横坐标x=0.10 m 不变,不同深度下5条频谱曲线、深度y=0.45 m 不变,不同横坐标x下6条频谱曲线如图6所示.

图6 传感器2的频谱曲线
显然,频谱曲线仍然具有表中的4个明显频段.可以发现,频段3 仍然与裂尖深度具有良好的相关性:随裂尖深度增加,频段3幅值降低.低频成分随着裂尖横坐标x的增加而迅速增长:当x<0时,低频成分较弱:当x>0时,低频成分很强.根据低频段的幅值,可以轻易地判断x的符号,即判断裂纹向左还是向右倾斜.
结合对两传感器信号频谱的分析,可以初步得出:当给定裂尖水平位置时,裂尖深度可由两传感器的响应频段3幅值反映;当给定裂尖深度时,裂纹在水平方向上的跨度(倾斜程度)可由传感器1的响应信号频段4的幅值进行反映,而裂纹倾斜方向可由传感器2的响应信号低频段的幅值来确定.能够把响应特征和裂尖位置建立一定关系,通过机器学习反演裂纹具有可行性.
按照此思路,对于双裂纹情形,在两裂纹之间设置与信号源关于裂纹开口处对称的传感器1、紧邻裂纹1的传感器2,在裂纹2右侧设置与其相距一定距离的传感器3、紧邻裂纹2的传感器4,如图7所示.由传感器1、2和3、4分别推测两裂纹深度,由传感器1和3分别判断两裂纹倾斜程度,由传感器2和4分别判断两裂纹倾斜方向.

图7 双裂纹情形下传感器布置方案
6 基于BP神经网络的裂纹反演
6.1 数据集和神经网络模型的建立
由于频谱特征集中于特定频率区间内,考虑在上一章所述4个频段中,以100 Hz作为间隔,提取每个频率对应幅值作为特征,见表2.
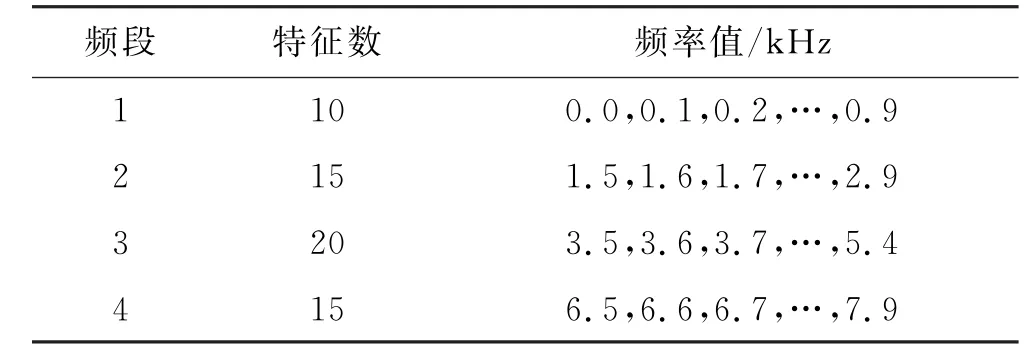
表2 各频段提取特征频率值
为了加快收敛,对标签和特征数组按列进行归一化处理,使得数据全部落在区间内:
式中:X i,Xnori分别表示数组第i列原始和归一化后的列阵.
将归一化后的标签和特征数组按照训练集80%,验证集和测试集各10%的比例进行切分,见表3.

表3 数据集切分
训练模型时,较小的学习率会导致需要更多迭代步数,而较大的学习率可能造成难以收敛,考虑使用随迭代步数而变化的学习率,采用指数衰减:
式中:βi为第i步学习率;β0为初始学习率;a,b表示每经b步,学习率衰减到1/α;经调整,取β0=0.1,a=2,b=100.
6.2 裂纹反演效果
为了增加预测精确度,每次训练-预测过程中所有可训练参数按照N(0,1)分布独立随机产生,并将训练—预测过程独立运行400次,以测试集预测结果的平均值作为裂尖坐标反演结果.某样本裂尖各坐标分量的预测情况和正态分布拟合曲线如图8所示(实际值为:x1=-0.4,y1=0.5,x2=0.4,y2=0.6,单位:m),均值与真实值较为接近.

图8 裂尖各坐标预测值分布
对各样本裂尖坐标分量预测值按照误差大小按区间进行计数,结果见表4~5.可以发现,除了双裂纹情形下对y2的预测外,绝大部分预测值误差在5 cm 以内,反演效果较好.总体上,该预测模型对裂尖横坐标的预测准确度高于纵坐标;双裂纹情形下,对裂纹1的预测准确度高于裂纹2.

表4 单裂纹各样本预测值按误差范围计数
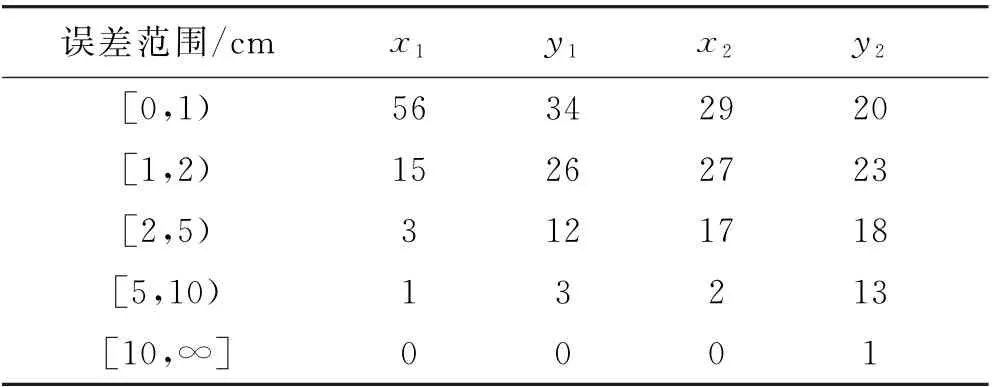
表5 双裂纹各样本预测值按误差范围计数
为了改善对y2预测的准确度,考虑在裂纹2右侧增加传感器,以增加输入特征数量.y2误差分布与新增传感器数量na的关系见表6.不难发现,增加传感器数量可以明显减小预测误差.在实际运用中,可以根据预期精度选择布置传感器数量.

表6 y 2 误差与新增传感器数量
7 结 论
提出了一种基于响应信号频域特征和BP 神经网络的裂尖位置反演方法,可用于对大体积混凝土结构中裂纹的实时无损检测.第一步,建立基于XFEM和吸收边界层的波动模拟模型,通过两主频正弦波的激励,波跨过裂纹传播,对不同位置的传感器造成不同的响应变化,提取特定频段的幅值作为特征,形成数据集.第二步,搭建BP神经网络,将训练数据集输入到神经网络,得到裂尖坐标的反演模型,再输入未知裂尖位置下的响应特征,可实现对该裂尖位置的预测.主要结论如下:
1)通过XFEM 实现带裂纹结构的建模,可以避免因裂纹改变而重新划分网格,大大减小了前处理的工作量,也便于基于节点编号提取特定点的响应.
2)采用吸收边界层可以在减小模拟域的同时,保证响应信号不受边界反射波的干扰,即可在裂纹附近的小区域内,模拟半无限模型的响应情况.
3)不同位置的传感器频谱曲线具有相同的特征频段,但幅值随裂尖位置的变化规律各不相同.特定传感器的特定频段呈现出与裂尖坐标分量的明显相关性,决定了以频域作为数据特征进行机器学习的可行性.同时,仅提取特定频段的幅值,相较于输入整个时域响应数据,大大减小了特征数据量,降低了模型训练成本.
4)该数据模型具有良好的准确度,且随采用传感器数量的增加,准确度可进一步提升.

