等几何连续介质弹性模型的带厚度布料仿真方法

任靖雯，戴俊飞，蔺宏伟*

1.浙江大学数学科学学院，杭州 310058；2.浙江大学计算机辅助设计与图形学全国重点实验室，杭州 310058

0 引言

随着布料在时尚电影、电脑动画和电子游戏等行业的广泛出现，布料仿真已经成为一个非常活跃的研究课题（靳雁霞 等，2021）。用户对更舒适逼真的视觉体验的追求，使如何兼顾更高的精度与更快的计算速度显得尤为重要。如今，布料仿真已在如虚拟试衣（Adikari 等，2020）、机器人辅助穿衣（Clegg等，2020）等新兴领域得到应用。在计算机图形学中，基于物理的方法在布料仿真中占主导地位，在视觉和物理上能合理反映出弹性体的不同物理特性。尽管常用的粒子系统模型及其加速方法可以实现高效的仿真，却难以准确描述布料弹性、粘性和塑性等真实的物理属性。这些属性可由连续介质的弹性动力学模型实现，利用经典有限元方法（finite element method，FEM）通过三角网格离散求解，直接描述动态过程的真实物理特性，但要达到理想的仿真效果所需网格单元较多，求解复杂耗时。因此，基于物理的布料仿真模型通常将布料建模为曲面和壳模型，对较厚布料的仿真能力较弱。

为实现准确、高效和稳定的变形，解决现有模型在建模方式、方法精度和计算速度的权衡问题，本文提出了一个带厚度的布料模型，并利用等几何分析进行快速求解。虽然等几何分析（isogeometric analysis，IGA）（Hughes等，2005）提出较早，但用于布料仿真的研究较少。据目前所知，仅将布料建模为壳模型（Lu 和Zheng，2014；Shin 和Lee，2020；Peng 和Zheng，2023）。本文方法的区别在于考虑到布料本身自带厚度的结构性质，将布料建模为三变量B 样条体表示的薄板模型，能够使用更少的自由度（degree of freedom，DOF）充分真实地刻画布料的形变。这样不仅很准确地描述了布料的物理属性，而且使仿真过程计算效率更高。基于物理的三维连续介质弹性动力学方程，利用等几何—伽辽金法推导出弱形式，通过张量积B 样条基函数同时构造精确的布料的物理几何形状和动力求解系统中每一时刻的位移，对方程弱形式离散化，嵌入到Newmark隐式动力学框架中，最终转化为在控制网格上求解小型线性系统。综上，本文主要贡献如下：1）提出了一个更真实直接的以三变量B 样条体建模的布料模型，适用于不同厚度属性的布料；2）利用等几何—伽辽金法在布料几何的控制网格上求解连续介质弹性形变问题，使用自由度更少，求解速度更快，布料光滑性更好。

1 相关工作

基于物理方法的布料仿真的研究可追溯到Terzopoulos 等人（1987）基于固体连续介质理论提出的弹性形变模型，通过构造描述材料弹性性质的系数，由拉格朗日动力学方程表示柔性体的形状和运动，模拟弹性效果。三十年以来，研究者们提出了许多创新的仿真方法及其加速方法。Provot（1995）将织物视为一系列由无质量的弹簧连接离散质点的网络，提出了反演动力学处理超弹性问题的质点—弹簧模型，随后广泛应用于模拟布料（Wang等，2020）、毛发（Jiang 等，2020）和肌肉软组织（Tang 等，2021）等仿真。虽然该模型求解速度快，但是人为假设的结构模拟机制过于简单化，无法保证弹性体变形中真实的物理特性。

为了加速求解，基于位置的动力学模型（Müller 等，2007）以非线性Gauss-Seidel 式的迭代局部投影每个约束，便于在GPU（graphics processing unit）上高度并行计算，不足的是刚度的控制与物理系数无关，收敛较慢，迭代次数不同，材料表现的刚度也不同。Liu 等人（2013）使用块坐标下降法替代传统牛顿迭代法，求解隐式欧拉积分下的质点—弹簧系统的能量最优化问题。整个线性系统在运行时保持恒定，每根线性弹簧约束可以在局部步骤中分开求解。这种全局/局部求解思想被推广为投影动力学模型（Bouaziz 等，2014），并且支持弹性能量具有特定二次形式的材料模型，并进一步扩展以支持更一般的材料（Liu 等，2017；Overby 等，2017），应用于干摩擦接触等问题研究（Li 等，2022）。尽管投影动力学在CPU 上直接求解很快，但在GPU 上求解速度并不理想。Wang（2015）以及Wang 和Yang（2016）提出了一种切比雪夫加速技术，可以同时应用于投影动力学和基于位置动力学，以加速收敛。Pall 等人（2018）将系统划分为红、黑着色的两个独立粒子集合，结合Gauss-Seidel 算法快速求解；Zhang（2020）基于CUDA（compute unified device architecture）框架来提高渲染性能；Li 等人（2020）提出了多GPU 并行的方法加速计算复杂的布料。此外，基于数据驱动的布料仿真方法（Chen等，2021；靳雁霞 等，2022）在损失一定精度下可获得实时仿真效果。

经典有限元方法布料仿真（Volino 等，2009）通过对连续体的三角网格逼近，从定义曲面模型的应变能量泛函出发计算弹性力，可以描述复杂的几何特征和不同的材料特性。针对弹力雅各比矩阵不定的情况，Kim（2020）利用快速的半正定投影法提出了Baraff-Witkin 能量下的有限元方法布料仿真。等几何分析（IGA）（Hughes 等，2005）是一种将几何设计与仿真分析无缝连接的数值方法。与经典有限元不同的是，它直接基于几何模型的控制网格计算，可避免有限元中网格生成的耗时长、存在逼近误差和自由度较多等问题。IGA将用于表达几何的NURBS基函数同时用于表示求解域，在控制网格上的计算可以使得精确计算只需要更少的自由度。NURBS更容易构造高阶连续的曲面和几何体，变形更加光顺，更节省 计算开 销。Lu 和Zheng（2014）将Kirchhoff-Love 壳模型应用于等几何分析中，通过曲率张量考虑弯曲函数，实现了完整的布料仿真流程。Shin 和Lee（2020）、Peng 和Zheng（2023）分别基于该壳模型扩充了等几何分析中的基函数模拟布料接触、断裂等问题和过拉伸问题。等几何的概念还应用于利用Bezier 样条曲面表示的布料的质点—弹簧模型中，得到了良好的效果（李鹏高 等，2019）。不同于这些布料的建模方式，本文从三变量B 样条体表示的薄板模型出发，模拟真实有厚度的布料结构，在等几何和Newmark 隐式积分的框架中求解连续介质弹性力学方程，更简便直观地实现动态仿真，在建模上比壳模型更真实客观，在精度上优于粒子模型，在求解速度上优于有限元方法。

2 预备知识

2.1 NURBS样条

在计算机辅助设计（computer aided design，CAD）中，p次B样条（Piegl和Tiller，1997）曲线定义为

式中，{Pi}，i=1，…，n是控制点，是定义在节点向量Ξ={u1，u2，…，un+p+1}上的p次B 样条基（Piegl 和Tiller，1997），且满足非递减性u1≤u2≤u3… ≤un+p+1。当首、末节点重复p+1 次时，称Ξ为开节点向量。

图1 分别展示了一维情况的不同次数下，在参数空间[0，1]中均匀节点的B 样条基函数的分布，每个区间[ui，ui+1]都有p+1个非零基函数。

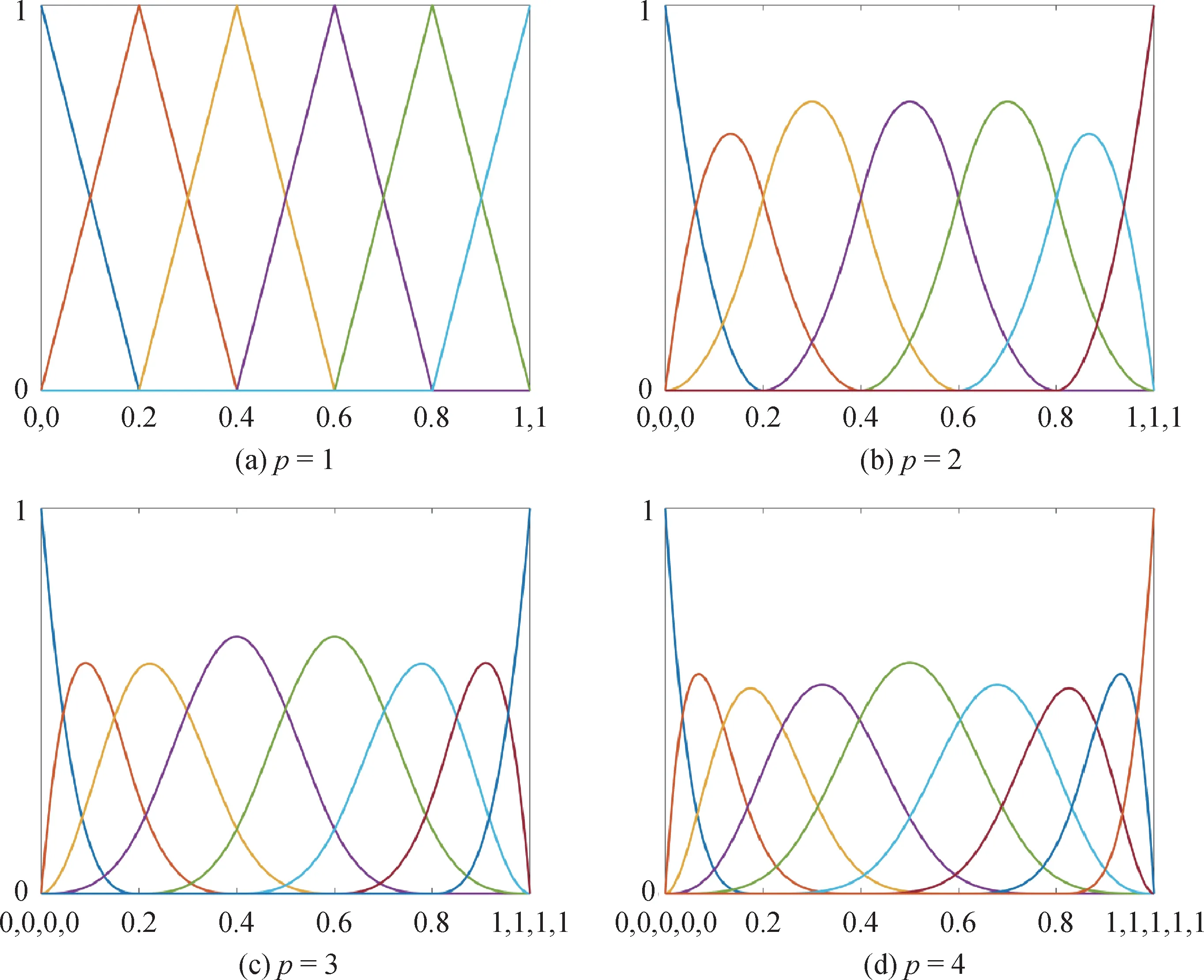
图1 不同次数的均匀B样条基函数示例Fig.1 Examples of uniform B-splines under different orders（（a）p=1；（b）p=2；（c）p=3；（d）p=4）

对于更复杂的曲线，特别是圆锥曲线，NURBS基函数有更精确的表示，定义（Piegl和Tiller，1997）为

式中，ωi为每个控制点Pi所对应的权重。当ωi都取值为1 时，NURBS 基等价于B 样条基。NURBS 样条曲面和体分别由二维和三维下的张量积表示。

2.2 线弹性动力学模型

基于物理连续介质的弹性变形模型可以用来模拟三维弹性体的物理特性，描述在给定边界条件下对外力真实合理的动态响应。考虑一个线性弹性动力学问题：几何物体Ω在时间[0，T]内受到外力f作用发生形变。令u∈R3表示笛卡儿坐标系下的几何体中任一点x∈Ω的位移。假设该物体为均匀且各向同性的，且物体的质量密度为常数ρ。弹性动力学的平衡控制方程（Zienkiewicz 等，2013）由下列初/边值PDE（partial differential equation）给出，具体为

式中，“ · ” 表示点积，表示位移对时间的一阶导数（即速度），ü表示位移对时间的二阶导数（即加速度），g：ΓD×(0，T) →R3是Dirichlet 边界条件。应力σ表示物体内部每单位横截面积的力，是一个对称张量。

一方面，由于受到外力作用，物体内部产生弹性应变ε。非线性的Green 应变给出了与位移的关系，对于一般小变形的弹性体，可用Green 应变的线性逼近形式，即Cauchy 应变，来表示几何方程（徐芝纶，2018），具体为

为了简便计算，将应变和应力张量用向量表示，具体为

因此，几何方程（4）可转化为

式中，B∈R6×3称为应变—位移矩阵，由位移关于空间坐标的一阶偏导数构成。

另一方面，本构法则将应变与应力关联起来，称为物理方程（徐芝纶，2018），通常采用胡克定律，具体为

式中，D∈R6×6为与物体材质相关的弹性系数矩阵，包含杨氏模量E和泊松比ν。因此，弹性动力学模型（3）中平衡方程转化为

2.3 等几何—伽辽金法

对于弹性体动力平衡方程（8），运用等几何—伽辽金方法（IGA-Galerkin）（Hughes 等，2005），首先需要将问题转化为求解下列弱形式方程，具体为

式中，权函数ω∈V={ω|ω∈H1(Ω)，ω|ΓD=0 }，试探解u∈S-{t}={u(·，t)|u(·，t) ∈H1(Ω)，u|ΓD=g}，H1(Ω)为一阶导数平方可积的函数的Sobolev空间。

等几何—伽辽金方法利用高阶连续光滑的样条基函数张成完备的有限维子空间，来逼近无限维空间St和V。对于B样条体表示的物理域，有

将位移数值解形式（11）代入弱形式（9），得到离散的矩阵方程（Hughes等，2005），即

式中，M=[Mi，j]，K=[Ki，j]，b=[bi]，具体计算为

式 中，Mi，j，Ki，j∈R3×3，bi∈R3，i，j=1，2，…，nml，M为整体质量矩阵，K为整体刚度矩阵，b为外部载荷向量，d(t)为t时刻未知位移的控制系数构成的向量，I为单位向量。在动力学中，由于阻尼作用引起的能量损耗，一般与物体质量和刚性有关。例如Rayleigh 阻尼矩阵C可以用质量矩阵和刚度矩阵的组合来表示。因此，求解线性弹性连续体的动力学PDE最终离散为求解线性系统（Hughes等，2005），即

几何模型的样条基函数和控制点代替了有限元分析中的单元形函数和节点，由此，等几何—伽辽金法的计算网格由有限元法中通过剖分生成的节点网格转移到了样条体模型本身的控制网格上。图2 中左图表示一个三变量—2 次B 样条体，中间是一个IGA 单元，由于样条基函数的局部支撑性，它仅由右图的3 × 3 × 3 的局部控制网格（基函数）控制，黑点表示控制顶点。因此，式（14）中矩阵具有稀疏性，利用IGA 单元的局部性质，整体矩阵由单元矩阵装配所构造。按照单元矩阵中的基函数的局部索引在全局中的索引累加得到整体矩阵，右端载荷向量也按照同样的规则累加。全局索引和单元中局部索引的对应通过预先创建矩阵IEN(e，b)=B来实现，表示第e个单元中的局部索引b对应全局中的索引B。

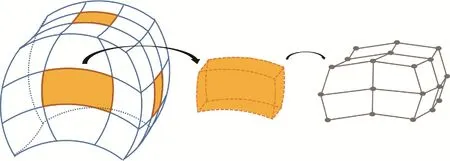
图2 三变量—2次B样条体的IGA单元和单元控制网格Fig.2 Trivariate-quadratic B-spline solid with its IGA element and the associated element control mesh

3 有厚度布料的等几何模型和求解

布料仿真的研究侧重点在于如何兼顾更高的精度与更快的计算速度。现有的模型有很多，但每个模型优势与局限并存。例如质点—弹簧模型（Provot，1995）、基于投影约束思想的位置动力学模型（Müller 等，2007）和投影动力学模型（Bouaziz 等，2014）虽然容易实现，但由于存在内部结构简化、物理不准确性和迭代时能量二阶导数采取近似可能导致收敛慢等情况，有限元方法模拟准确但所需自由度太多，计算相对复杂。因此，考虑到布料本身的厚度，采用三维连续体介质弹性力学模型模拟薄板状布料，利用等几何分析求解可使仿真效果在物理上高保真，并且耗时又不会太长。

3.1 等几何—伽辽金布料模型

利用三变量B 样条体构造薄板模型来模拟有厚度的布料几何V(u，v，w，t)，如式（10）定义，由于布料在厚度方向的网格形变较小，因此在该参数方向上自由度至少可以取2，使用线性基函数，在一定程度上也减轻了体模型自由度的负担，而其余两个参数方向上则可视具体问题而定。在厚度方向的尺寸尽可能小（1 mm 左右）。同时，对弹性动力学方程（14）中的位移解uh(u，v，w，t)由式（11）表示。等几何—伽辽金布料模型基于样条体的控制网格计算（如图3），使得计算所需的自由度大幅减少，控制网格的形变即意味着布料的形变或位移。

图3 B样条体布料模型控制网格的变形Fig.3 The deformation of the control mesh of the B-spline cloth model

式（12）中，Mi，j，Ki，j∈R3×3，bi∈R3，这里将方程中整体矩阵M，K和b构造为

式中，ne=(n-p)(m-q)(l-r)表示IGA 单元个数，令nb=(p+1)(q+1)(r+1)表示B 样条局部基函数个数，下标i′，j′是影响第e个单元中的控制点的全局索引，(i′，j′)分别可以由IEN(e，i)和IEN(e，j)得到。分别为单元质量矩阵和单元刚度矩阵，为单元载荷向量，利用在单元上的高斯积分计算。Ki，j中Bu通过链式法则得到，具体为

图4 展示了双2 次B 样条基函数下的等几何—伽辽金法装配整体矩阵的过程，图中局部基函数个数为9，每个单元矩阵包含9 × 9个元素。

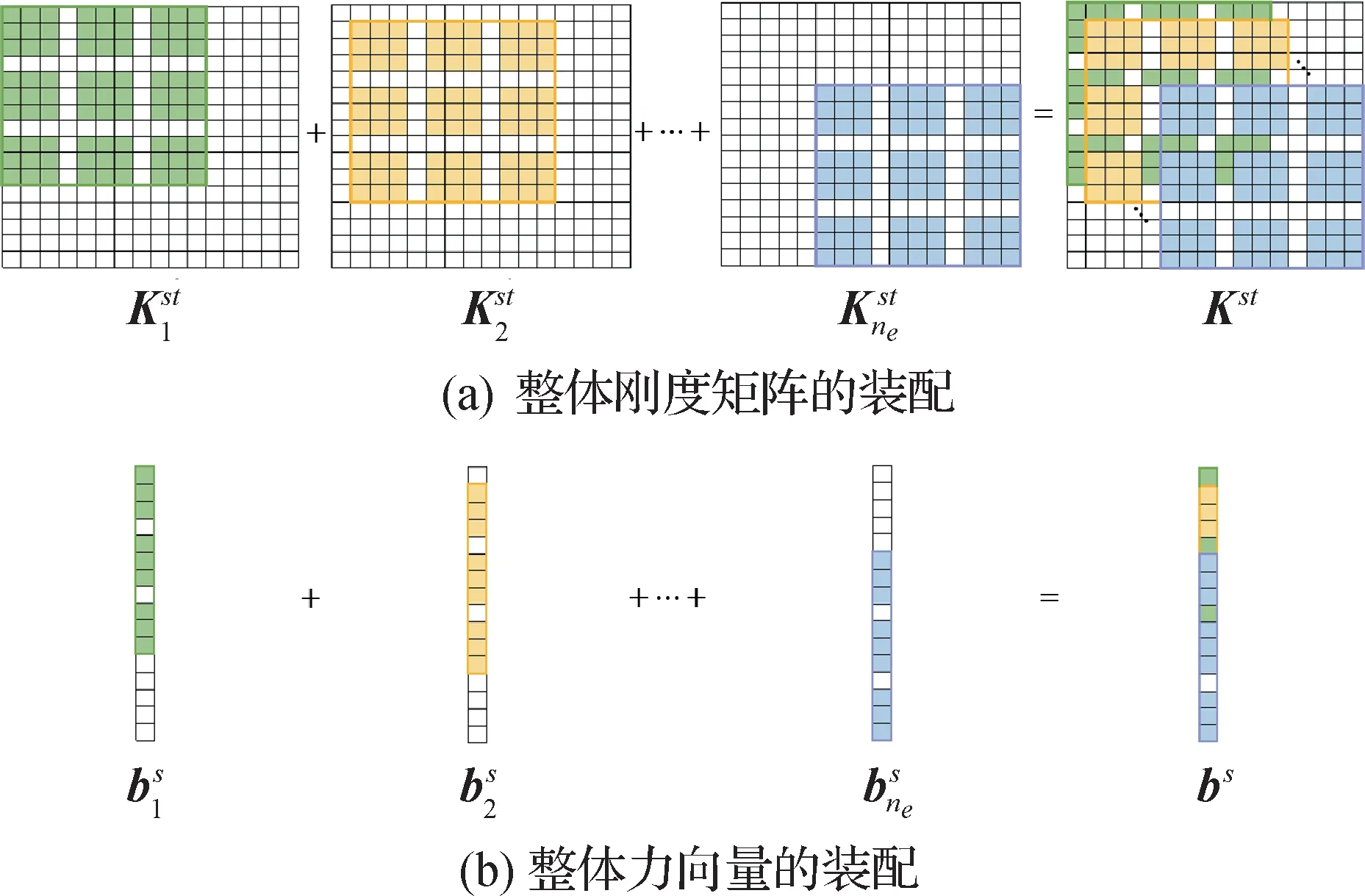
图4 由单元矩阵装配整体矩阵示意图Fig.4 The assembly of the global matrices from the element matrices（（a）the global stiffness matrix；（b）the global force vector）

3.2 时间积分求解

实时性和稳定性是仿真的重要目标，其中计算耗时最大的部分在于迭代过程。时间积分方案主要分为显式、半隐式和隐式。显式和半隐式计算效率较高，但稳定性较差，时间步长的选择依赖于单元的最小尺寸，而时间步长取值太小容易导致漫长的求解时间。隐式积分的求解和时间步长无关，一般具有无条件稳定性，每次迭代都需要求解大型线性方程组，在处理复杂模型时更新速度较慢。在实际应用中，弹性体变形仿真必须满足高效稳定的需求，这里采用隐式Newmark 积分方法，可以允许较大的时间步长以节省计算时间，并且在一定条件下满足无条件稳定。它将更新位移u和速度v时所需的加速度a视为上一时刻已知的加速度和当前时刻未知的加速度的加权和。利用二阶精度下无条件稳定的Newmark 积分的平均加速法（Zienkiewicz 等，2013），具体为

在布料的仿真过程中，将阻尼矩阵C省略，而采取直接在更新当前时刻速度时加以限制的策略，即μv，这里使用统一的阻尼系数μ。将时间积分代入矩阵方程，可得

3.3 边界条件

对于布料模型的弹性仿真求解，线性方程组（19）需要结合式（3）中Dirichlet 边界条件，采取高斯消元算法。记方程组（19）为

将所有控制点的全局索引集合记为I，边界点和内部点的索引集合记为Ibd和Iint，则有I=Ibd∪Iint。当前时刻在边界点处的位移由Dirichlet 条件给出，即利用更新式（18）可得出边界点处在当前时刻的加速度，具体为

将Lt中与Ibd中索引对应的所有列提取出来构成矩阵，其中#(Ibd)为边界点个数。所以求解方程组（20）转化为求解方程组

线性系统（22）的求解可以用基于矩阵分解的直接法求解，也可使用迭代求解，如牛顿迭代法、共轭梯度法和GMRES（generalized minimum residual）等。对于迭代法可能出现收敛慢的问题，有时需要对方程进行预处理，不完全Cholesky 分解等。由于本文的等几何布料模型只需使用较少的自由度，且为对称正定，因此采取直接求解的方式即可。

因此，除了几何参数，如自由度（n，m，l）和基的次数（p，q，r），弹性体的变形效果主要由质量参数ρ、刚度参数（E，ν）和阻尼力参数μ决定。整体求解流程框架如图5所示。

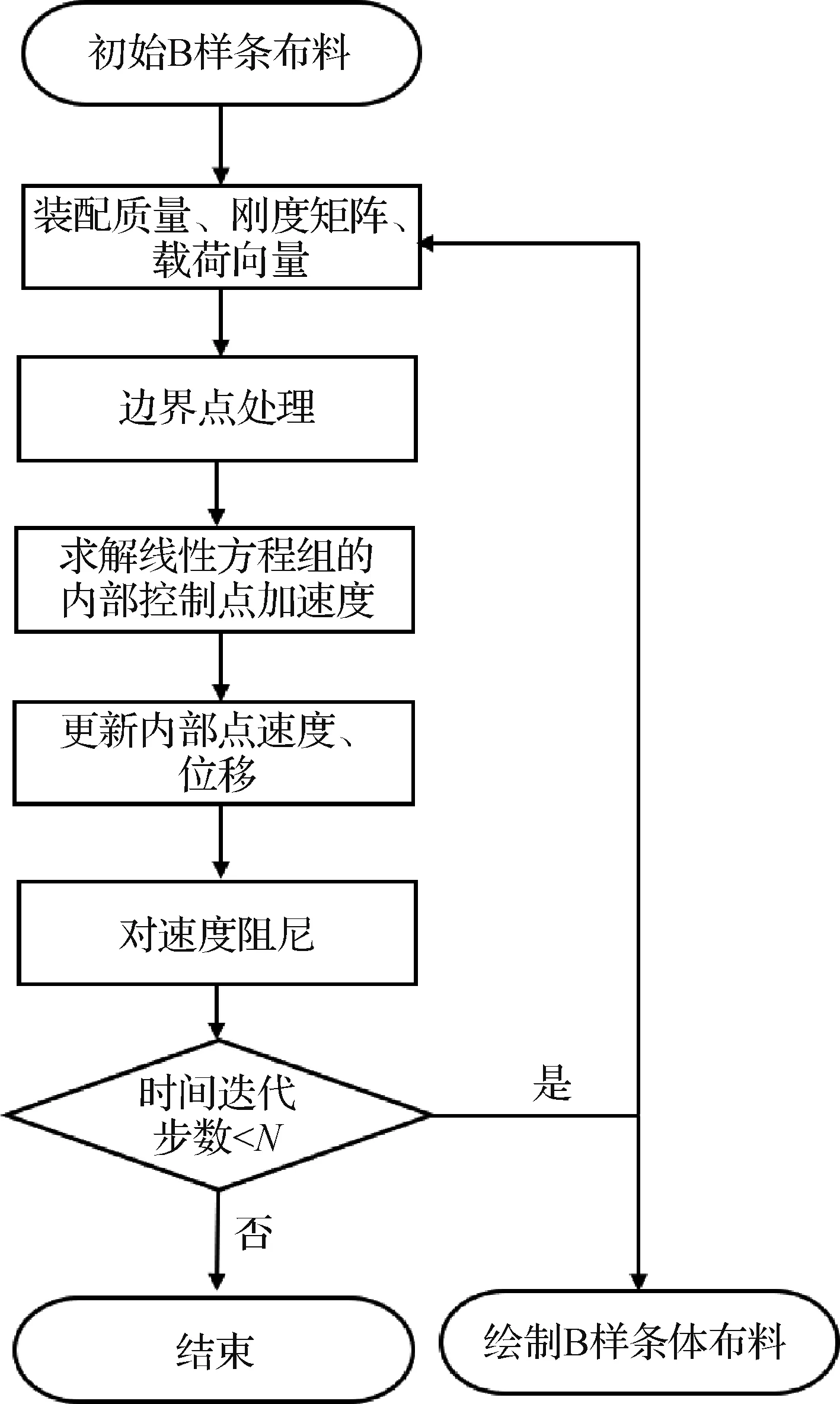
图5 等几何—伽辽金布料模型求解流程Fig.5 The flowchart of the cloth simulation with IGA-Galerkin method

4 实验结果与分析

针对提出的基于等几何—伽辽金法求解弹性动力学问题下的布料仿真框架，本文对影响仿真效果的各个因素进行了对比和探究。在Visual Studio 2017 Eigen 库和Houdini 的仿真环境下，实验均在Intel i7-7700 3.60 GHz CPU，16 GB 内存的台式电脑上进行。在隐式时间积分中，时间步长选取为0.005 s。为提高仿真速率，装配整体矩阵利用openMP 并行计算，式（17）中基函数的偏导可以预计算。

4.1 等几何—伽辽金模型与经典模型对比

首先模拟在受重力下，两种目前常用的布料模型两端固定悬挂的仿真效果：质点—弹簧模型和投影动力学模型。选择10 × 10的质点—弹簧网格，弹性系数和阻尼系数分别设为100 和0.05，质点的质量密度为1，在考虑所有的结构弹簧和剪切弹簧情况下，布料的网格和仿真效果如图6（a）所示。在投影动力学模型中，选择相同密度的网格，拉伸和弯曲刚度系数都设为10，阻尼为0.005，总质量为1，布料的形变效果如图6（b）。质点—弹簧模型的网格变形较大，不可避免地会出现过度拉伸的现象，更类似于橡胶，且存在自交情况，在没有后处理矫正的情况下真实感较弱；投影动力学模型可有效避免过拉伸问题，但网格自由度太少使得布料光滑性较差。当自由度为10 × 10 × 2 时，利用薄板模型的等几何—伽辽金法，用三变量B样条体构造布料形状和位移数值解，形变后的控制网格和效果如图6（c）。在布料长宽方向都使用二次B样条基，杨氏模量和泊松比分别为105和0.3，质量密度为1，阻尼系数取为0.5。

图6 不同布料模型的网格和仿真效果对比Fig.6 The simulation results of different cloth models

在相同网格密度下，3 种模型都能模拟布料下落的运动，前两种无法对布料本身的材料属性准确控制，而本文模型更符合布料的弹性和粘性性质，在变形中更加光滑，模拟厚布料更合适。当外力始终存在时，布料会一直处于变形状态，而外力消失时，也表现出一定的塑性而不能完全恢复原状。物理响应可直接通过弹性物理参数调控，在适当参数选取下的布料控制网格更规则化，更易于分析。

为了衡量FEM 和IGA 方法模拟布料的计算量，本文以自由度为10 × 10 × 2 的二次IGA-Galerkin 方法在迭代一定的时间步长之后得到的布料仿真结果为例，对其进行密度不同的六面体网格离散化，用以得到经典FEM 方法下的相同时间步长的仿真结果。选择相同的100 × 100 × 2 个参数点，根据两个结果的均方根误差（root mean squared error，RMSE）来衡量视觉效果的相似度。通过实验对比发现，当RMSE ＜ 0.04 时，本文的IGA 方法与经典FEM 得到的布料结果在视觉效果上相近，此时IGA 的自由度为10 × 10 × 2，而FEM的自由度至少为32 × 32 × 2，此时的FEM 比IGA 在CPU 上的计算速度更慢，如表1 所示。同时，本文模型还与壳模型IGA（Peng 和Zheng，2023）的仿真结果进行了对比，布料厚度都设为0.001 177 m，其他参数尽可能保持一致，最终也能得到相似的结果，但本文的模型计算时间更短，如表1所示。

表1 IGA-Galerkin布料与经典FEM和壳模型IGA的时间开销对比Table 1 Time cost comparison between IGA-Galerkin cloth and classical FEM and shell-based IGA

因此，样条表示的布料具有更高阶的连续性和光滑度，在达到理想的仿真效果和光滑度下，本文模型在时间效率上比连续介质经典FEM、壳模型IGA更高。本文模型在网格质量、光滑度和逼真度等仿真效果上均优于质点—弹簧模型和投影动力学，达到理想效果时所需自由度少于FEM，计算开销更小，在厚度与壳模型IGA一致下计算时间也更短。

4.2 布料仿真场景

模拟了一边和两端点固定的布料受重力和阻力垂落摆动的场景，在不同时刻的形状及位置分别如图7和图8所示。布料初始为静止状态，当受到重力时，布料开始下落，图7（a）和图8（a）都处于下落状态，并有继续往前运动（图7（b）和图8（b））的趋势，由于阻尼达到上升最高点导致不能再上升，布料下落并褶皱增多（图7（c）—图7（f）和图8（c）—图8（f）），表现为往返摆动。本文模型能逼真地模拟布料摆动的运动过程，在端点处的拉伸不会像质点—弹簧模型那样过大（图6），B样条构造使得布料的光滑度良好。

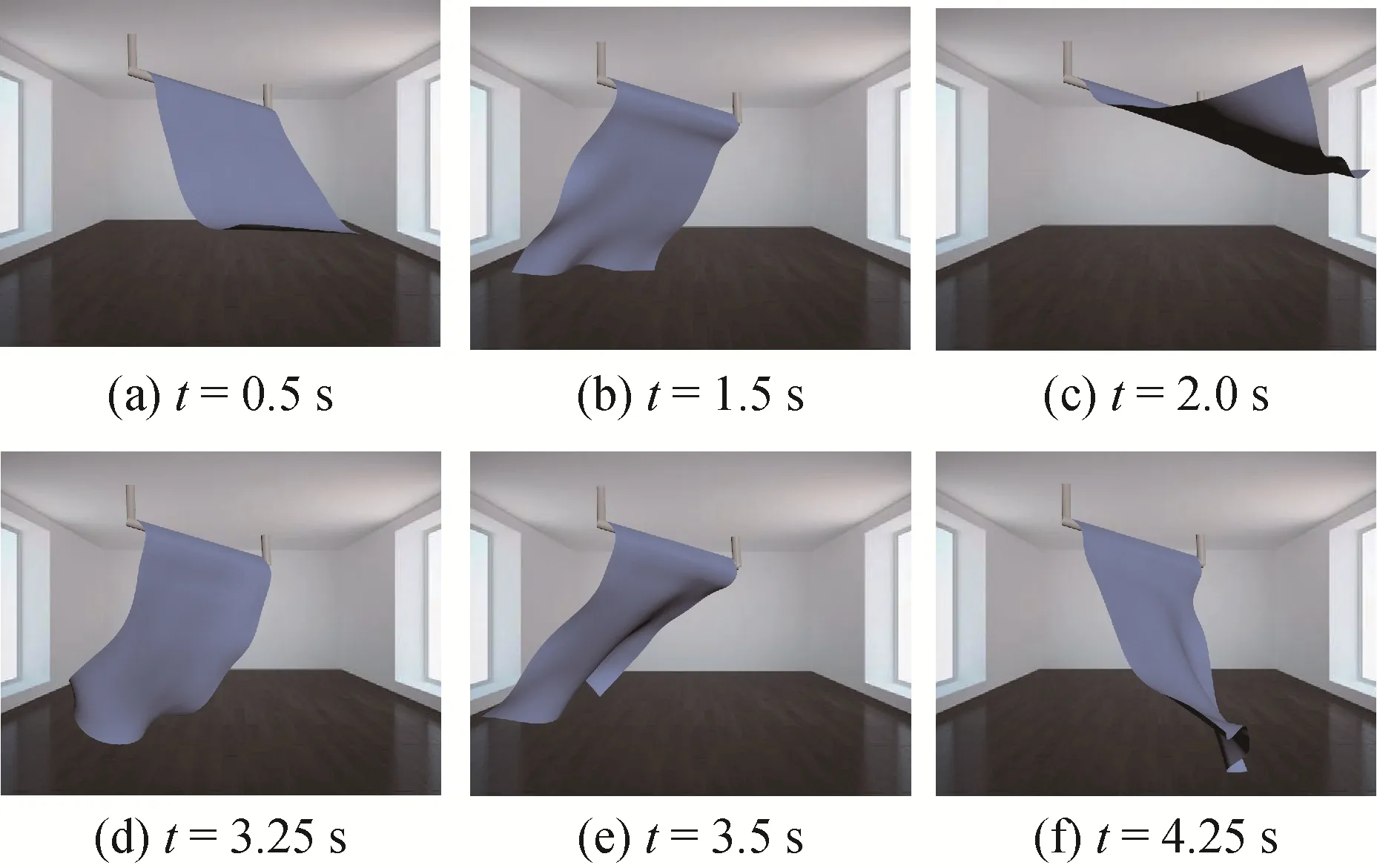
图7 顶端一边固定的布料垂落场景Fig.7 The hanging cloth fixed on one side of the top

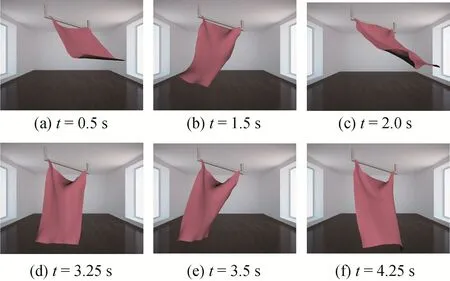
图8 顶端两点固定的布料垂落场景Fig.8 The hanging cloth fixed on two points on the top

对于布料的碰撞接触问题，只需检测样条体模型的控制网格是否有碰撞、自交，可以减少计算量，如图9所示。

图9 布料与地面接触场景Fig.9 The contact between the cloth and the ground

本文提出的布料模型在厚度方向具有可控性，对于不同厚度属性下的布料，等几何布料模型可以通过对厚度方向的参数的调控，准确模拟有厚度布料的变形，比如皮革、帆布类材质的厚布料。图10比较了不同厚度尺寸对仿真效果的影响，更薄的布料比更厚的布料的飘动摆幅会更大。图11 比较了在厚度方向上不同次数的基函数对仿真效果的影响，整体效果与线性基（图10（a））差异不大，因此考虑到计算开销的问题，本文实验使用线性基。

4.3 参数的影响

在等几何分析中，节点加细和升阶操作都会提高求解精度，而不会改变物理域的样条体几何形状。本文首先探讨了网格的稠密度对布料仿真效果的影响，对粗糙网格进行不同层次的加密，截取在t=1.025 s 的状态进行对比，如图12 所示。其中，k=0表示粗网格，网格规模为5 × 5 × 2；k=1、2、3分别表示网格加密1、2、3 次，网格规模分别为10 × 10 × 2、15 × 15 × 2、20 × 20 × 2。需要说明的是这里的加密指直接使用不同密度的网格，与节点插入有所区别。布料尺寸相同大小，其他参数保持一致，当控制网格密度越大时，即自由度越大，布料的褶皱细节越多。

图12 不同自由度的布料在t =1.025 s的状态Fig.12 The cloth simulation results of different DOFs at t =1.025 s （（a）k =0；（b）k =1；（c）k =2；（d）k =3）

图13是对图12（b）参数下的布料进行不同层次的k-细化后在t=1.7 s 截取的效果对比，即用不同阶B 样条基构造布料几何和位移解，p=2、3、4 表示在u，v方向（布料的长和宽）分别取双2 次、双3 次和双4 次，w方向（布料的厚度）保持线性。可以得出，在其他参数相同时，阶数越大，布料在各方向上呈现的弯曲细节越多、光滑性越好。

加密和k-细化操作对布料的仿真效果有提升作用，如图14 所示，初始控制网格为2 × 10 × 10，在v，w方向上取二次样条基函数，分别将网格加密和升阶以及混合操作，布料的仿真效果有相应的区别。值得注意的是，实验中不同顺序下的两个混合操作，最终生成的基函数对应的节点向量相同，所以仿真效果相同。网格加密和k-细化都能使布料褶皱细节增多，函数升阶能使布料光滑性更好、更逼真。不同时刻自然垂落的旗帜如图15所示。

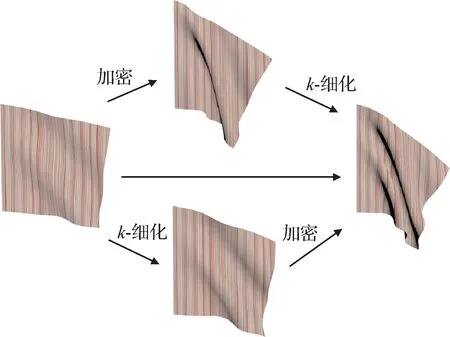
图14 网格密度和基的阶次对布料仿真效果的影响Fig.14 The effects of the mesh density and the order of the basis on the cloth simulation

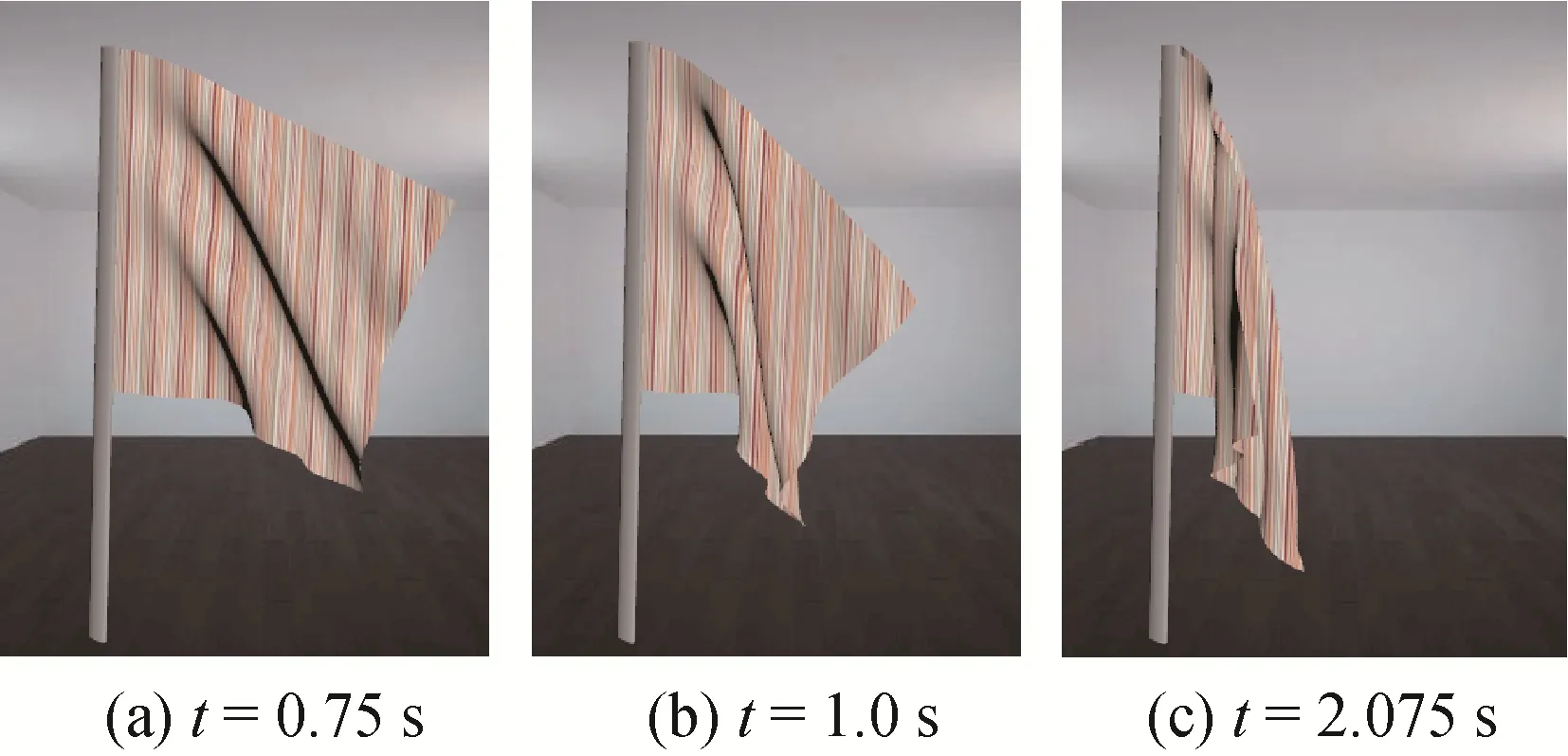
图15 不同时刻自然垂落的旗帜Fig.15 The snapshots of the falling flag

各项几何参数和物理参数见表2。网格密度和基的阶次对布料仿真速率的影响如表3所示。

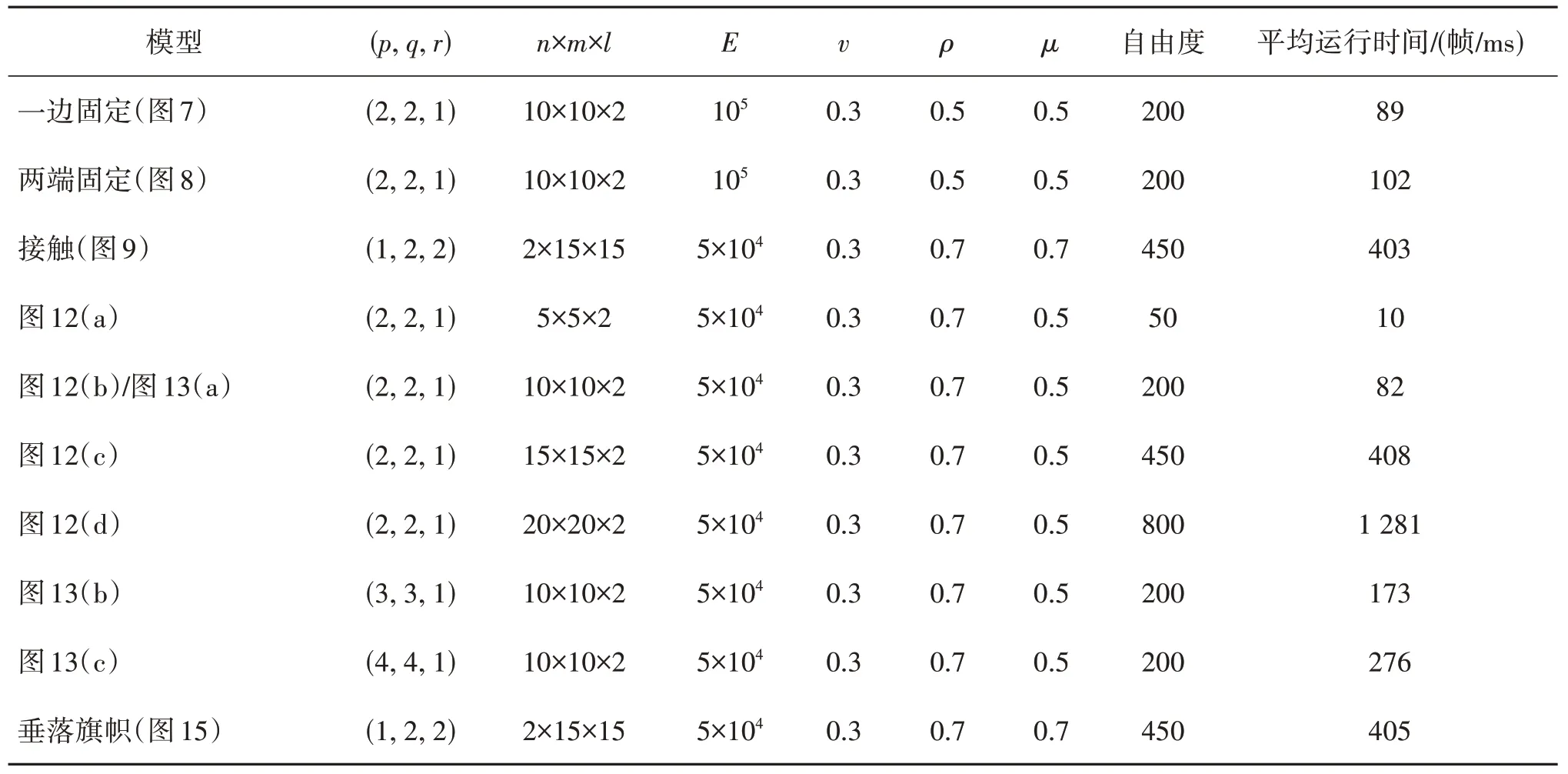
表2 IGA-Galerkin布料模型参数表和仿真时间Table 2 The parameters of the IGA-Galerkin cloth model with the simulation time

表3 网格密度和基的阶次对布料仿真速率的影响Table 3 The effects of the mesh density and order of the basis on simulation time/ms

物理参数的选择对仿真效果有着直接的影响，通过模拟一端固定垂落的布料场景，本文对不同参数选取下的情况进行了实验和总结，如表4所示。其中，“可行性”代表效果的物理合理性是否可接受，“描述”是对不可行情况的问题 表述。

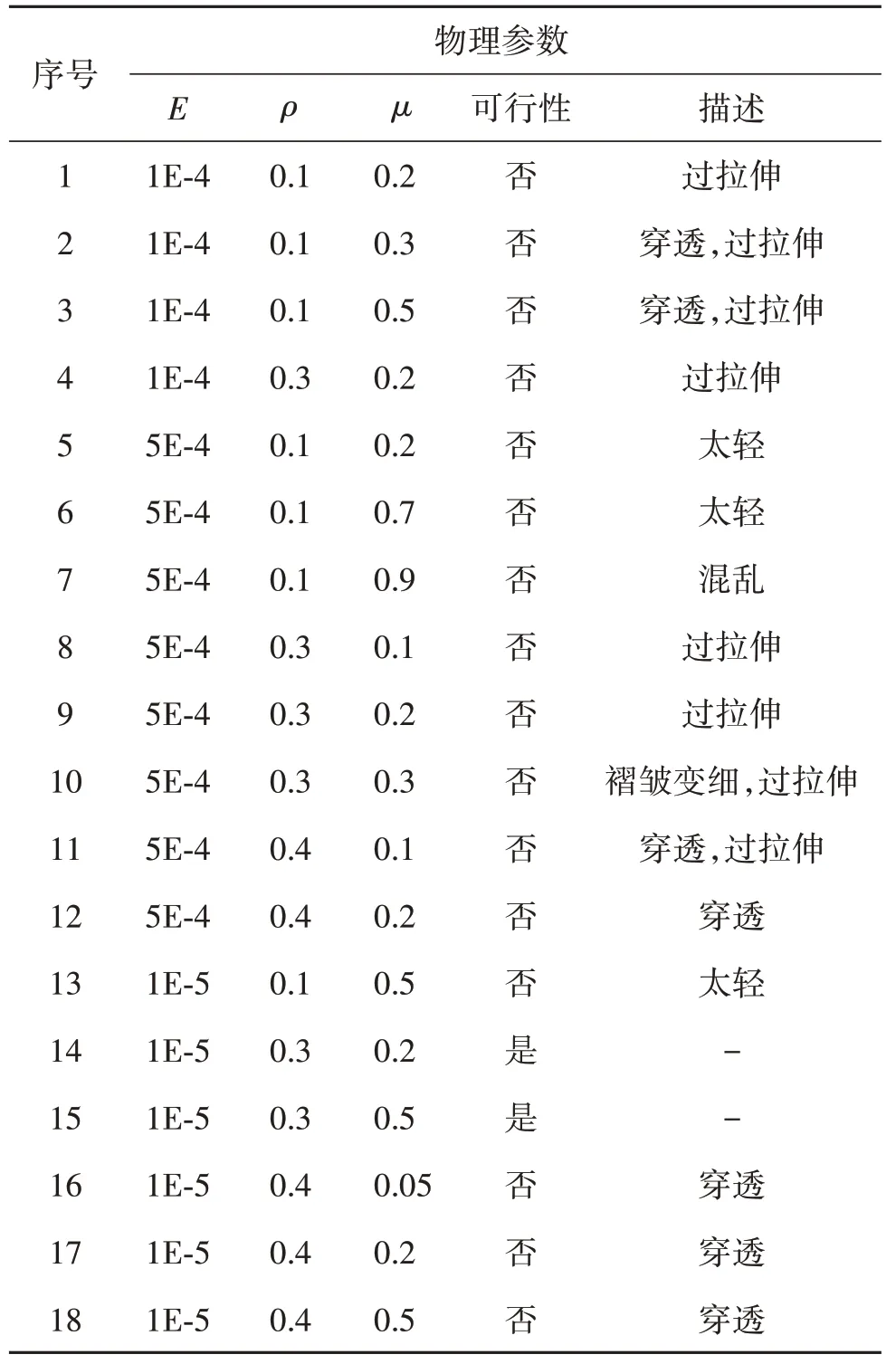
表4 物理参数对仿真效果的影响Table 4 The effect of the physical parameters on simulation results

从表4 可以看到，参数的不恰当选取会使得模型结果出现问题，例如过拉伸、质量太轻瓢浮空中和穿透等，如图16 所示。这些不可避免的问题在前人工作中已有许多相应的特殊处理，如超拉伸修正、碰撞自交检测与响应等。在本文模型适当的参数下，可以在一定程度上获得可接受的效果，同时这些处理任务也可在控制网格上完成，计算开销更小。由于泊松比的变化范围一般较小，表示延长拉伸时的横向收缩性，此处设为0.3。从1～12组实验中可知杨氏模量太小，都会由于弹性过大引发过拉伸问题；从5～12组、13～18组实验中可知，质量密度设置过小会使布料瓢浮无法下落，质量密度过大会造成布料穿透。由于实验条件有限，无法测量实际阻尼，此处阻尼系数可根据质量密度调控，阻尼系数过大也会造成穿透现象。因此，根据实验中的规律，对于不同的几何参数下的模型，可通过调节物理参数控制布料的仿真效果。

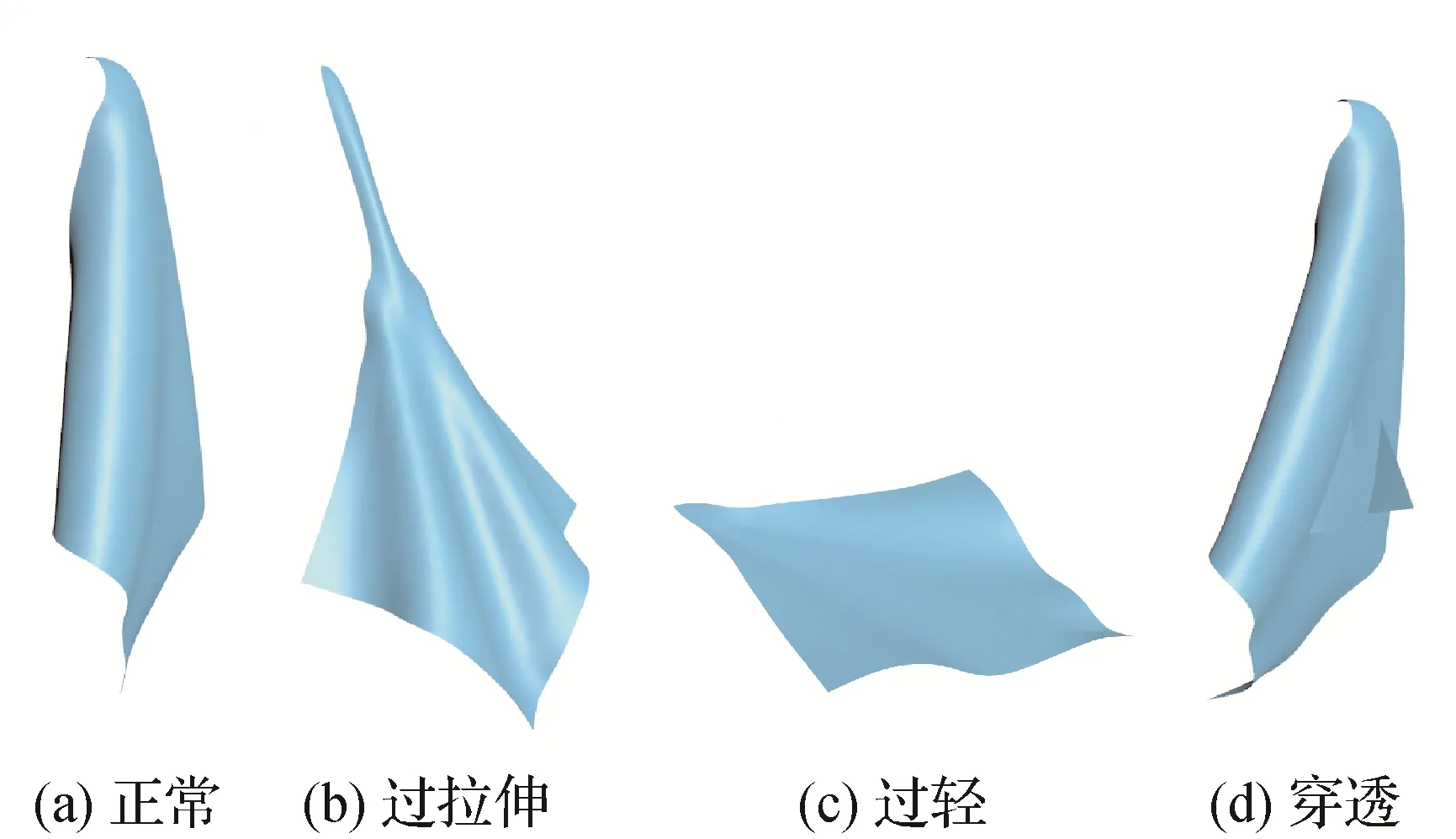
图16 物理参数选择不当出现的仿真问题Fig.16 Simulation artifacts caused by improper selection of physical parameters（（a）the normal；（b）super-elongation；（c）floating；（d）penetration）

5 结论

本文针对基于物理方法的布料变形仿真问题，利用等几何—伽辽金的思想，提出一个利用三变量B 样条体的薄板模型模拟带厚度的布料的仿真框架。本文首先建立了线弹性连续介质力学的弹性动力学控制方程，然后在一定边界条件下转化为方程的弱形式，进一步在等几何—伽辽金和Newmark 隐式积分的理论下离散化得到线性方程组。为了加快运算速度，装配矩阵的并行计算和预计算是有必要的，最后求解线性系统得到仿真结果。实验表明，在取得恰当的物理参数下，本文方法模拟效果良好逼真，并且B样条模型使得自由度降低，减小了计算开销，布料的光滑性更好。

虽然基于线性弹性问题来模拟布料仿真能生成较好的模型效果，但对于实际物体表现的更多的是非线性的大变形行为。未来的工作可利用等几何—伽辽金法的优势，从非线性问题着手建立布料模型求解及对其进行加速的高效方法以及适用于样条体控制网格上的碰撞检测、自交穿透和过拉伸等仿真问题的处理方法。