从图卷积网络到图散射网络：回顾与展望

柳世禹，戴文睿，李成林，熊红凯

上海交通大学电子信息与电气工程学院，上海 200240

0 引言

随着深度学习在图像、音频等传统信号上取得成功，视觉场景分类（Espinace 等，2010；Zhou 等，2021；Miao 等，2021；Zhou 等，2022b）、目标识别（Xu等，2023；Zhou 等，2022a）以及语义分割（Noh 等，2015；Wei 等，2022）等任务已经从花费高昂的人工特征提取转变为深度卷积神经网络（convolution neural network，CNN）和递归网络（recurrent neural network，RNN）中基于超参数的自适应表征学习。而图表征学习技术的发展，为目标检测、语义分割等传统任务提供了新的思路。例如在人体动作分类与预测任务（Pan 等，2021；Li 等，2022）中，可以将视频中人的骨骼框架逐帧提取，通过构建时空图进行表征学习来完成人体动作的分类及预测。图表征学习也广泛地运用于更高阶的新型计算机视觉任务当中。如在点云任务中（Wang 等，2019a；Wang 等，2019b；Qian 等，2021），常常通过K-邻域构图以及对边赋予权重来描述点云的空间结构与分布，通过图卷积等操作聚合邻域特征，提取点云的信息。在3D流形与网格的分类上（Monti 等，2017；Perlmutter 等，2020），可以在网格的每个顶点建立不同大小的感受野来学习流形的局部和整体的几何特征。

然而，面向传统信号的卷积神经网络和递归神经网络的输入顺序是有意义的，将其直接用于图信号的表征学习存在诸多问题。图没有固定的节点顺序，因此图信号的表征学习应当满足排序等变性（Zou 和Lerman，2020）。虽然可以通过输入随机重排序来学习重排序等变性，但在图任务上的提升依然十分有限。况且图的大小是任意的，具备复杂且不一定规则的拓扑结构，每个节点可能拥有不同数目的邻接点，节点与邻接点之间边的权重也不一定相等。图网络（graph neural network，GNN）（Caelli等，2002；Scarselli 等，2009；Micheli，2009）和图卷积网络（graph convolution network，GCN）（Kipf 和Welling，2017）的提出解决了卷积神经网路和递归神经网络在图数据学习上失效的问题。图卷积网络主要分为空域图卷积网络（Hamilton 等，2018；Veličković等，2018；Monti 等，2017）和谱域图卷积网络（Levie等，2019；Li等，2018b；Tang等，2019；Wang和Zhang，2022）两大类。谱域图卷积拥有坚实的信号处理的理论基础（Sandryhaila 和Moura，2013a，b，2014）和谱图理论基础（Chung，1997），通过谱域滤波来学习图和图信号的特征。空域图卷积网络则通过图的邻域特征聚合进行表征学习。随着图卷积网络的发展，早期基于空间邻域特征聚合的图卷积网络的缺点也逐渐显现：由于搜索的邻域节点数量会随着图卷积网络的层数呈指数增长（Chiang等，2019），且每个节点的聚合特征都需要储存，当图比较大的时候会产生巨大的空间占用。同时，由于卷积层数过深容易产生过平滑现象，使得节点的特征无法分辨，因此基于空间邻域聚合的图卷积网络大多比较浅（Chen等，2020）。虽然跨层连接和稠密连接能在一定程度上缓解特征过平滑问题（Li等，2019），但空域图卷积网络本质上依然是一个低通滤波器（Nt 和Maehara，2019）。

散射变换最早由Mallat（2012）提出并应用于图像表示，采用多尺度小波滤波器组为滤波核将L2空间进行划分，通过多方向多尺度的滤波核提取图像的特征。相较于卷积神经网络，散射网络具备更好的可解释性，且基于多尺度小波的卷积操作保证了散射网络中总能量的收敛性。同时，散射网络还具备平移不变性和较强的对信号扰动的稳定性。散射网络在传统信号的表征学习上取得了成功，并逐渐受到更多的关注，采用不同小波的散射网络也越来越多地应用于图分类（Cheng 等，2016；Shen 等，2021）等任务中。由于图傅里叶变换和传统信号的傅里叶变换存在一定的相似性，Gama等人（2018）将面向欧氏空间数据表征学习的散射变换拓展到图上并提出了图散射变换（graph scattering transforms，GSTs），采用扩散小波（Coifman 和Maggioni，2006；Coifman 和Lafon，2006；Bremer 等，2006）对图信号进行几何分析以提取多分辨率特征。基于多尺度小波滤波器组的图散射网络本质上是不可训练的谱域图卷积网络（Ioannidis 等，2022），保留了散射变换在信号处理中的可解释性以及对信号噪声和图拓扑扰动的鲁棒性（Gama 等，2019），且不同散射路径的输出特征呈多样化，不存在过平滑问题，因此在图分类、节点分类等任务中具备优势。

随着图信号处理技术的蓬勃发展，学术界开始对图信号处理的方法与模型进行总结以降低研究的时间成本。目前，国内外已有诸多图网络的综述与调研工作。Bronstein 等人（2017）在主要讨论图嵌入的基础上总结了部分图网络，Hamilton 等人（2018）总结了早期基于矩阵分解、随机游走矩阵和图卷积的图网络，Battaglia 等人（2018）讨论了图网络技术对归纳偏置、关系推理以及组合生成的影响，Lee 等人（2019）着重讨论了图网络中的注意力机制，并将相关图网络根据输入类别、注意力机制类型以及任务进行分类。Zhou 等人（2020）总结了主要图网络模型（包括谱域图卷积、空域图卷积、门控图神经网络以及图长短期记忆网络等）的特征聚合表达式以及特征更新表达式，降低了学习图网络的时间成本。唐朝生等人（2021）总结了医学图像深度学习中的图卷积的发展历程和技术，Wu 等人（2021）和Krzywda等人（2022）对图网络的不同模型、数据集、学习工具以及应用进行了系统性的归纳，分析了不同图网络模型之间的共性和区别，魏文超等人（2022b）介绍了图网络的背景与局限性，通过将图卷积处理方法分为正则化方法和架构调整方法，归纳了图网络层级信息挖掘算法。然而，目前仍没有关于图散射网络的综述，因此有必要对图散射网络技术、应用以及理论发展进行系统性归纳。

本文首先介绍图的相关背景知识和图与图矩阵的定义，从图卷积网络入手，对图卷积网络的技术与应用进行归纳，总结了现有的图卷积模型（包括空域图卷积模型和谱域图卷积模型）及其应用，指出了空域图卷积模型中的过平滑问题以及谱域图卷积网络模型表达能力不足的问题。然后对图散射网络的技术应用及数学理论进行归纳，阐述了图散射网络相较于空域图卷积网络和谱域图卷积网络的优势，分析了目前图散射网络技术和理论存在的局限性，并提出了图散射网络未来可能的研究方向。

1 背景知识与定义

1.1 图与图矩阵

在本文中，采用G=(V，E)来表示图，其中，V为图的顶点的集合，E为边的集合。对于时空图（spatio-temporal graph），采用三元组G=(V，E，X(t))来表示，其中Xt∈Rn×d为t时刻下的图节点信号。本文将图的邻接矩阵记为A，对于节点vi和vj，若边(vi，vj) ∈E则Aij=1，否则Aij=0。对于比较复杂的图，每条边的权重不一定相等，则令Aij=wij(∀ (vi，vj) ∈E)，此时A为带权邻接矩阵。对于节点vi∈V，其邻域 定义为N(vi)=将图的度矩阵记为D，D为对角阵，且有图拉普拉斯矩阵L=D-A，图网络中常用图拉普拉斯矩阵为归一化图拉普拉斯矩阵Lsym=I-D-1/2AD-1/2。为了简化表达，在没有特殊说明的情况下，用L表示Lsym。图邻接矩阵和图拉普拉斯矩阵均可作为一幅图的表示，即图位移算子（graph shift operator，GSO）。为了保证在谱域图卷积中网络的稳定性，通常采用重归一化图拉普拉斯矩阵作为图位移算子。为带环邻接矩阵，的度矩阵。常用的图位移算子还包括随机游走矩阵和惰性随机游走矩阵，分别如所示。本文的常用符号和定义如表1所示。

表1 符号与定义Table 1 Definitions and notations

1.2 图傅里叶变换与图信号卷积

根据归一化图拉普拉斯矩阵特征分解，图傅里叶变换（graph Fourier transform，GFT）定义为

式中，U=[u1，u2，…，uN]，为归一化图拉普拉斯L的特征向量矩阵，U*和u*分别为U和u的共轭转置。图傅里叶变换等效于将信号x投射到另一个特征空间中，遵循帕斯瓦尔定理。图傅里叶逆变换（inverse graph Fourier transform，IGFT）定义为

式中，为频谱的第l个分量。根据图傅里叶变换和图傅里叶逆变换的定义，以及定义在图G上的卷积操作*G，图信号x1与x2在图上的卷积的表达式为

如果把x1视为定义在图G上的离散滤波器，则图信号卷积的本质是对信号x2进行滤波操作。

1.3 图滤波器设计

在谱域图卷积中，一般情况下需要对图滤波器进行设计或训练自适应滤波器以达到最佳的特征提取效果。早期的谱域图卷积网络为了避免图位移算子的特征分解，大多采用多项式对目标滤波器进行逼近（Cheung等，2020；Gama 等，2020c），包括Chebyshev 多项式（Chebyshev polynomial）（Defferrard 等，2016），Cayley 多项式（Cayley polynomial）（Levie 等，2019）等。然而，谱域图卷积中常常需要用到窄带图滤波器来提升分类、分割等任务的效果，采用多项式进行逼近往往需要高阶多项式才能将误差控制在较小的范围内，不仅会引入更多参数，计算图位移算子的高阶表达会产生巨大的算力消耗。因此，Tseng（2020）提出了分式图滤波器，通过一系列多项式系数αn和βn，用更小的阶数来拟合陡峭的图滤波器。具体为

为了解决Tseng（2020）工作中滤波器分母趋于0 可能导致的不稳定现象，ARMA（auto-regressive moving average）滤波器（Bianchi 等，2022）给出了更一般的稳定的分式谱图滤波器表达式。具体为

采用不同的系数αn和βn，ARMA 滤波器能够设计出一系列不同的低通和带通图滤波器。

1.4 图小波

图小波最早由Hammond 等人（2011）提出。给定含有N个顶点的图G及其对应的图位移算子S=UΛUT，Hammond 等人（2011）对t尺度下第n个节点的小波系数进行定义，使得图小波同时在空域和谱域上是紧支的。具体为

式中，λl为图位移算子S的第l个特征值。式（6）在谱图卷积中的描述为

在图散射网络的后续工作中，常常采用扩散小波（Coifman 和Maggioni，2006；Bremer 等，2006）对图或图信号进行表征学习，即

在一般情况下，图位移算子S通常为惰性图扩散矩阵或惰性随机游走矩阵

2 图卷积网络

2.1 空域图卷积网络

与卷积神经网络考虑图像像素点的邻域特征相似，空域图卷积网络主要考虑图节点邻域内的特征关系。空域图卷积网络也可用于传统图像的分类，通过将图像的像素点视为图的节点，对图像进行构图。空域图卷积通过聚合邻域节点和中心节点的特征对中心节点的特征进行更新，从而提取高阶特征。

DCNN（diffusion-convolutional neural network）（Atwood 和Towsley，2016）将图卷积视为一个信号扩散的过程，采用随机游走矩阵来描述从中心节点到邻域各节点的概率。DCNN将图卷积的过程描述为

式中，P*由一系列多阶随机游走矩阵Pk拼接构成，因此，DCNN 在特征聚合中考虑了不同大小的邻域 。PGC-DGCNN（partition graph convolutiondiffusion graph convolution neural network）（Tran 等，2018）考虑k阶内的带环随机游走矩阵j≤k），为了增强图卷积网络的表达能力，PGCDGCNN 对不同阶数的随机游走采用不同的可学习参数矩阵，同时考虑了不同大小感受野内的节点特征，提升了图卷积网络在图分类任务上的表现效果。与随机游走矩阵不同，MixHop（high-order graph convolutional archetectures via sparsified neighborhood mixing）（Abu-El-Haija 等，2019）通过拼接多阶归一化拉普拉斯矩阵提取的特征对节点特征进行更新。

考虑到空域图卷积在多节点图上的局限性，GraphSAGE（graph sample and aggregation）（Hamilton等，2018）提出了采用固定数目邻居节点特征的方法来节省存储空间和计算时间。对于节点v，其邻域定义为从集合{u|u∈V，(u，v) ∈E}中的k均匀采样。若该节点的度小于k，则进行重复采样。GraphSAGE的特征更新表达式为

式中，fAGGREGATE（· ）可以为均值聚合、长短记忆网络聚合或池化聚合。

FastGCN（fast learning with graph convolution network）（Chen 等，2018）同样注意到了空域图卷积在多节点图上搜索节点数呈指数爆炸的问题。与GraphSAGE 不同，FastGCN（Chen 等，2018）不再对每个节点的邻居进行采样，而是基于当前子图节点对全图节点进行采样，大幅减少了子图中的节点数，节省了时间和存储空间的开支。Huang 等人（2018）根据图的权重矩阵以及当前子图的节点来计算下一层图卷积网络中每个节点被采样的联合分布条件概率，使得图卷积网络上下两层的联系更加紧密。与逐层的节点采样方法不同，Cluster-GCN（cluster graph convolution network）（Chiang 等，2019）采用图聚类算法从原图中采样出子图，通过仅在子图上进行图卷积的方式来节省训练多节点图的时间和存储空间。

GAT（graph attention）（Veličković 等，2018）将注意力机制引入空域卷积网络中，将图的邻域类比为注意力窗口，通过可学习参数矩阵W和注意力参数（Attention）来衡量节点vi和vj之间关系的紧密程度。具体为

为了凸显图的自身结构，GAT 仅考虑节点vi邻域内所有节点对其的注意力参数。为了方便注意力参数的比较，GAT 采用softmax 对注意力参数进行映射得到vi域内各节点的重要性程度αij=fsoftmax(eij)。基于注意力参数对邻域内特征进行聚合，就构成了GAT的特征更新策略，即

同时，GAT 也提出了多头注意力机制（Vaswani等，2017）。GaAN（gated attention network）（Zhang等，2018a）考虑到多头注意力机制的每组特征空间并不是同等重要的，引入可学习参数来调节每组特征空间的重要性。在GAT 的基础上，Chen 等人（2021）提出了面向多关系图表征学习的模型 r-GAT（retional graph attention network）。与GAT 和多头注意力机制模型不同，r-GAT 同时考虑节点的对象特征和关系特征，对解耦特征（disentangled features）进行学习，每个通道的特征均表示对象语义的一部分，因此更适用于下游任务的表征学习。

与上述图卷积网络不同，DGCNN（dynamic graph convolution neural network）（Wang等，2019a）采用特征K-邻域构图，基于各点当前的特征对没有固定图结构的点云进行动态构图以提取点云高阶的空间结构信息。构建邻域后通过邻域特征聚合来进行表征学习，具体为

式中，hΘ(·)为中心特征xvi的特征更新策略，□可以为任何特征聚合函数（如求和或最大池化）。

受到DGCNN 的启发，MPU（patch-based progressive 3D point set upsampling）（Wang等，2019b）和PUGCN（point cloud upsampling using graph convolutioni network）（Qian 等，2021）分别提出了稠密边卷积网络和空洞图卷积网络。稠密边卷积通过稠密连接增强特征的流动性和隐藏特征的多样性，而空洞图卷积网络通过聚合中心点附近不同跳数的邻居点的特征，实现多尺度特征的提取。AM-GCN（adaptive multi-channel graph convolution network）（Wang 等，2020）同时采用空间K-邻域构图和特征K-邻域构图两种方式，使特征能够同时在几何空间和特征空间传递，以多通道特征聚合的方式提高模型的表征学习能力。

表2 总结对比了空域图卷积网络的模型和任务。由于涉及邻域采样方法的采样邻域不变，但实际作用于特征更新的邻域会随着采样变化，因此“邻域动态变化”的指标对这类方法不适用。空域图卷积的主要优点在于其与传统卷积网络的相似性，能够考虑局部空间内的特征。然而随着网络层数增加，空域图卷积往往伴随着过平滑问题，虽然Li 等人（2019）提出的稠密连接图卷积网络（dense graph convolution network，DenseGCN）和跨层连接图卷积网络（residual graph convolution network，ResGCN）能在一定程度上缓解过平滑问题，但基于特征聚合的空域图卷积本质上是一个低通滤波器（Nt 和Maehara，2019）。

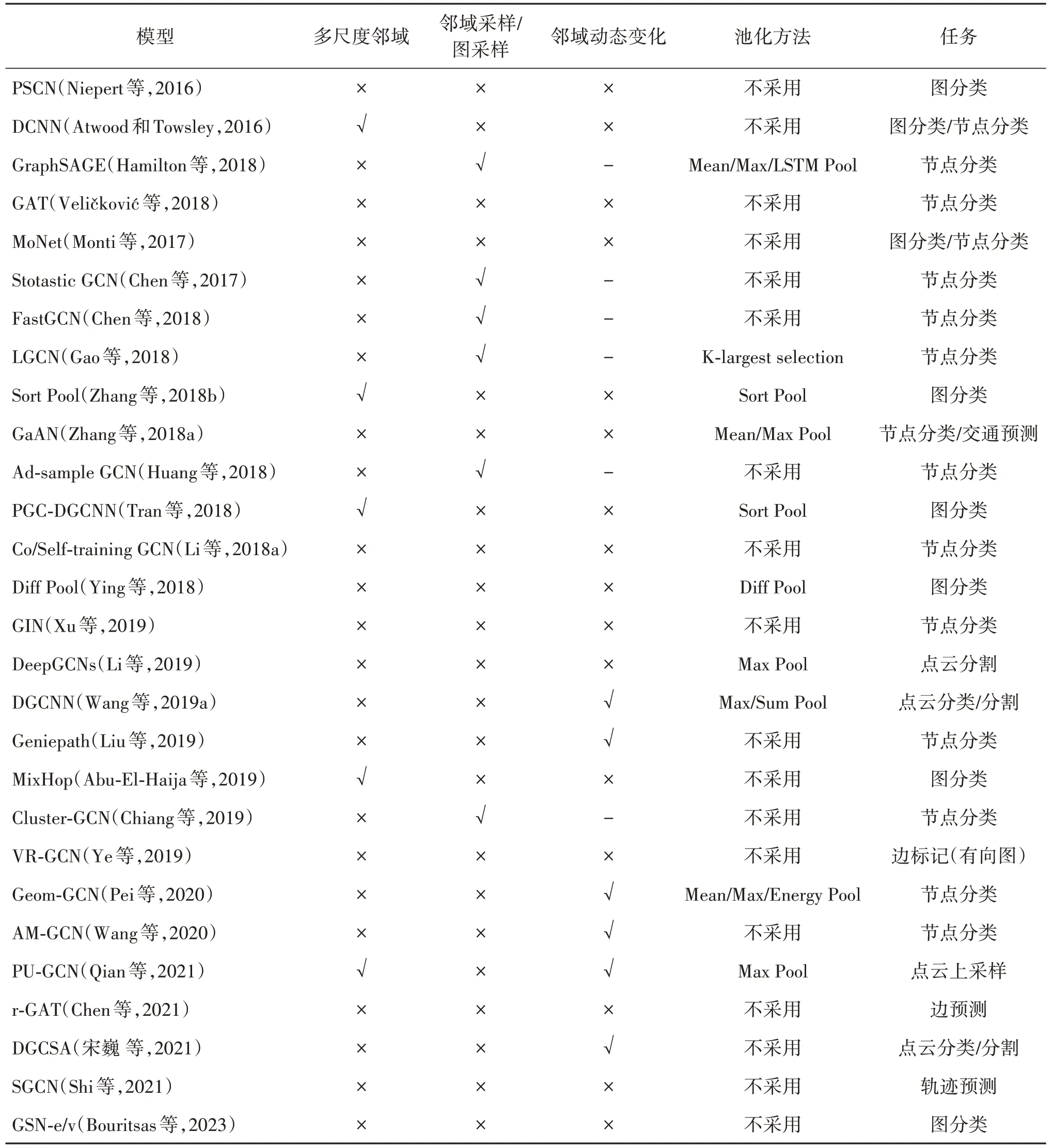
表2 空域图卷积网络模型的对比与总结Table 2 Comparison of works in spatial graph convolution neural networks

2.2 谱域图卷积网络

与邻域特征聚合的空域图卷积网络不同，谱域图卷积网络主要基于图傅里叶变换进行谱域滤波，从信号处理的角度进行图与图信号的表征学习。将面向传统信号的谱域卷积神经网络拓展到图上面临以下困境：图拓扑的扰动会导致图位移算子的特征向量矩阵发生变化，且矩阵分解的复杂度为O(N3)，对于多节点的复杂图需要的计算资源高昂。因此在应用中，常常使用多项式逼近（Hamilton 等，2018；Chen 等，2020）来避免图位移算子的特征值分解。最早的谱域图卷积由Bruna 等人（2014）提出，通过归一化图拉普拉斯矩阵L的特征向量把信号投射到谱域上，以谱域滤波的方式对信号进行卷积。具体为

式中，gθ(Λ)为关于L特征值对角阵的函数。在Bruna 等人（2014）方法的基础上，Henaff 等人（2015）将自适应滤波器引入谱域图卷积中，通过对角参数矩阵Θg=diag(θ1，…，θN)学习定义在谱域上的离散滤波器，赋予谱域图卷积网络更强的学习能力。令gθ(Λ)为定义在谱域上的多项式滤波器，具体为

由于多项式滤波器能等效为一组归一化图拉普拉斯矩阵的多项式，即

因此，可以通过多项式逼近谱域滤波器的方式来避免L的矩阵分解以节省算力。Defferrard 等人（2016）采用Chebyshev 多项式（Hammond 等，2011）来逼近谱域滤波器，即

式 中，Tk(·)为Chebyshev 多项式，满 足T0(x)=1，T1(x)=x，2xTk(x)=2xTk-1(x) -Tk-2(x)，=2Λ/λmax-IN，λmax为L的最大特征值。

将所有特征值映射到［-1，1］的区间内。在Chebyshev 多项式逼近的基础上，Kazi 等人（2019）同时用多个不同最高阶的滤波器对输入特征进行卷积，并把提取的特征通过拼接或最大池化的方式组合到一起，提出了Inception-GCN（receptive field aware graph convolution network）。

GCN（Kipf 和Welling，2017）进一步将λmax简化为2，通过采用1阶Chebyshev 多项式逼近的方式，将谱域图卷积描述为

为了防止过拟合并增强图卷积网络的泛化性，GCN将上述参数进一步简化为θ0=-θ1=θ。为了确保多层图卷积网络的稳定性，GCN 采用重归一化图拉普拉斯矩阵来限制谱域的范围。具体为

事实上，GCN 的卷积形式等效于1-跳特征扩散（Zhuang 和Ma，2018），因此也可以视为基于邻域特征聚合的空域图卷积网络。

然而，Chebyshev 多项式对于窄带滤波器的逼近并不完美，往往需要极高的阶数才能在较小的误差内逼近窄带滤波器。Levie 等人（2019）注意到这个缺陷，提出了Cayley多项式对谱域滤波器进行逼近。Cayley 多项式是一系列系数包含虚数的多项式，基于该多项式定义的Cayley滤波器为

式中，c=(c0，c1，…，cr)为一个实数和r个虚数组成的元组，h为频谱细化参数。Chebyshev 多项式可以等效为Cayley多项式中的一种特殊情况。与构造多项式谱域滤波器不同，Tseng（2020）和Bianchi 等人（2022）构造了分子和分母均为多项式的分式滤波器来更好地拟合频率响应衰减陡峭的滤波器，分别如式（4）（5）所示。

与多项式图卷积不同，AGCN（adaptive graph convolution network）（Li 等，2018b）将L视为可学习参数，通过函数F(L，X，Γ)对图拉普拉斯矩阵进行更新，将谱域图卷积改写为

式中，Γ为参数。AGCN 让特征的流动不再局限于图本身的拓扑结构，有助于发掘非邻接点之间的隐藏关系。APPNP（approximate personalized propagation of neural predictions）（Gasteiger 等，2022a）则通过PageRank 算法导出固定的K阶滤波器来进行图卷积，即

式中，fθ(X0)为特征矩阵X通过两层全连接网络后的结果，α为超参数，Xl为网络第l层的特征。APPNP 能够在不增加图卷积层数的情况下就提取到多跳距离内的邻接点的特征。

除了上述谱域图卷积，GDC（graph diffusion convolution）（Gasteiger 等，2022b）通过图转移矩阵T=D-1/2AD-1/2进行K阶扩散进行谱域图卷积，即

Wu等人（2019）认为谱域卷积可以继续简化，移除了层间的非线性激活函数以及不同阶数的转移矩阵，提出了更加简便高效的谱图卷积模型SGC（simplifying graph convolution network），仅在输出层设置可学习参数并通过softmax层输出结果。具体为

SGC采用加权带环邻接矩阵A′=A+γI及其对应的归一化拉普拉斯矩阵L′ 和转移矩阵T′=D′-1/2A′D′-1/2，将最大特征根从2 限制到1.5 左右，在保证图滤波器在谱域不发散的情况下避免了滤波器在谱域上可能出现负值的情况。在马尔可夫扩散核的基础上，Zhu 和Koniusz（2020）提出了S2GC（simple spectral graph convolution），具体为

相较SGC，S2GC 在低频和高频滤波器间做了权衡，使得谱域滤波能同时兼顾图的全局信息和节点的局部信息。

受到SGC 和GCN 的启发，Chen 等人（2020）提出了GCN2来解决GCN 中参数过少导致的表达能力欠缺以及特征过平滑问题。GCN2中的图卷积形式为

式中，αl和βl为超参数。通过跨层残差连接以及ResNet（residual network）（He 等，2016）中的恒等映射使得GCN2既能在谱域内组合出K阶内任意系数的滤波器，又能在网络层数增加时较好地避免特征过平滑问题。

表3 对比总结了谱域图卷积的模型与应用。一方面，谱域图卷积采用传统信号处理的方式对输入特征进行滤波操作，为图卷积提供了独立于空域图卷积以外的思路；另一方面，基于归一化图拉普拉斯矩阵或转移矩阵的谱域图卷积在空域上存在几何含义，有的谱域图卷积（如：GCN（Kipf 和Welling，2017））几乎等同于基于邻域的特征聚合，将谱域图卷积和空域图卷积联系了起来。谱域图卷积虽然可以通过设计图滤波器来避免空域图卷积中的过平滑问题，但传统谱域图卷积网络中每一层卷积操作仅通过一个滤波器，可学习参数少，生成的表征往往比较单一，使模型欠缺表达能力。

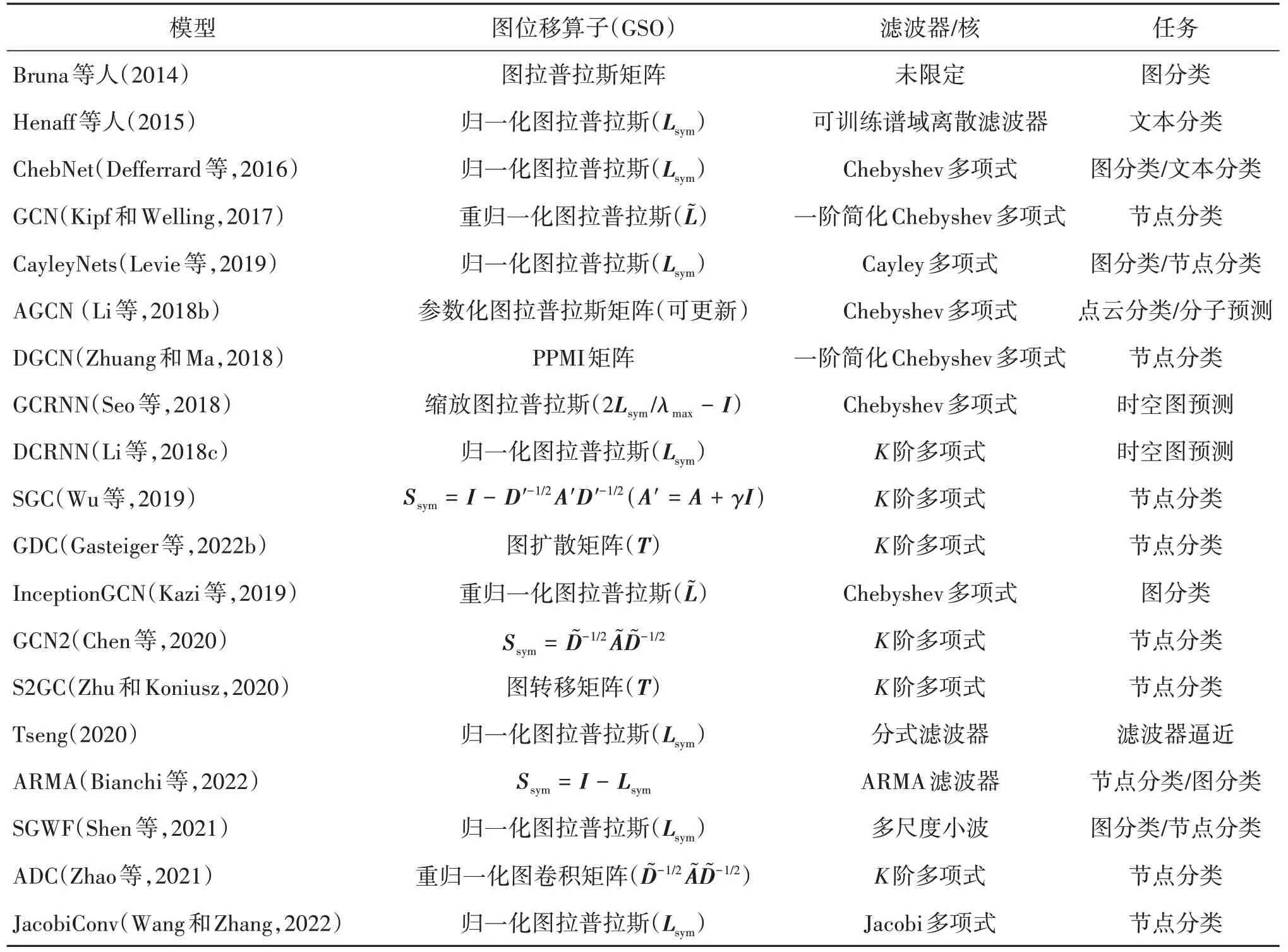
表3 谱域图卷积网络模型的对比与总结Table 3 Comparison of works in spectrum graph convolution neural networks

3 图散射网络

3.1 图散射变换

图散射变换最早由Gama等人（2018）提出，将面向传统信号的散射变换（Bruna 和Mallat，2013）拓展到图上。通过图位移算子在图的谱域上构建起一系列多尺度小波滤波器组{ψj，φJ}对图信号的频带进行划分。图散射网络（graph scattering network，GSN）的主要结构由图1所示。将图卷积操作记为*，输入信号x通过图散射网络第1 层中的节点时输出特征φJ*x，并向下一层的各节点传递不同的散射特征|ψj*x|(0 ≤j≤J-1)。图散射网络每一层中的每个节点都通过相同的操作输出该路径上的散射变换特征，并向下一层传递散射传递特征。

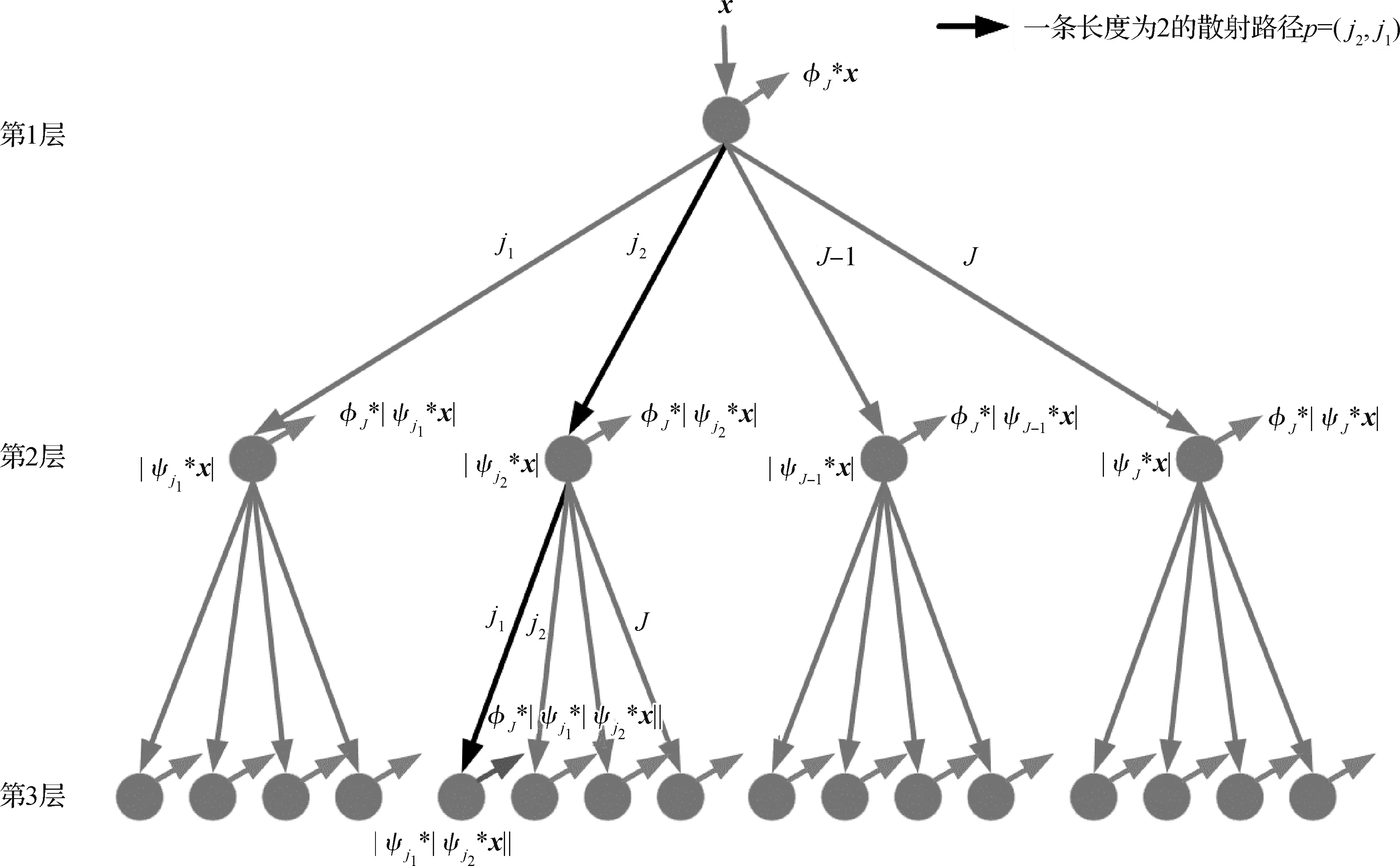
图1 3层图散射网络的主要结构。Fig.1 The structure of a GSN with 3 layers and 4 filters

对于一条长度为l的散射路径p=[p1，p2，…，pl] (0 ≤pi≤J-1)及与其对应尺度的一系列小波{ψp1，…，ψpl}，定义在该路径上的图散射传递算子为

与散射变换的定义相似，定义在路径p上的图散射变换为

式中，φJ为J尺度下的尺度函数。对于空的散射路径p=∅，图散射变换定义为S[G][∅]x=φJ*x。将长度为l的所有散射路径构成的集合记为Pl，对于一个M层的图散射网络，将长度小于M的所有散射路径输出的特征收集起来就构成了x的图散射变换特征。图散射网络采用取模来引入非线性变换，避免了不同散射路径上的特征重合的问题，使得图散射变换特征更加多样化。

图散射网络本质上是不可训练的谱域图卷积网络。相较于空域图卷积网络，由多尺度小波滤波器组构成的带通滤波器避免了特征过平滑的问题；同时，由于图散射网络的散射路径随层数呈指数增长，即便不可训练，图散射网络依然能够输出多样化的特征，弥补传统谱域图卷积网络输出特征比较单一导致的模型表达能力不足的问题。

3.2 图散射网络的变型与应用

3.2.1 传统图散射变换及应用

最早的图散射变换（Gama等，2018）采用惰性图扩散矩阵作为图位移算子，通过引入扩散小波（Coifman 和Maggioni，2006；Bremer等，2006）进行图散射变换。扩散小波的空域表达式为

扩散小波在空域和谱域上均具备局部性。Perlmutter 等人（2023）证明了非对称图位移算子构建的小波与对称图位移算子构建的小波在图散射变换中存在相似性，将图散射变换中的图位移算子进行了推广。在后续工作中，Gao 等人（2019）采用非对称的惰性随机游走矩阵来构建扩散小波。在传统的空域图卷积网络中，采用的特征聚合形式会丢失高频的有用信息，而ψjx能够提取中心频率各不相同的带通特征，从而提高表征中的信息含量。Perlmutter 等人（2020）对传统的黎曼流形进行离散采样转化为图，并通过图散射变换学习黎曼流形的局部几何特征。

在上述工作的基础上，Min 等人（2020）采用S=作为图位移算子，将图散射变换与传统图卷积网络（Kipf 和Welling，2017）相结合来解决GCN中的特征过平滑问题，Scattering GCN（scattering graph convolution network）（Min 等，2020）采用GCN和图散射变换来分别提取输入信号的低通特征Xgcn，l和带通特征Xsct，l，通过将低通和带通特征进行拼接，Scattering GCN 成功提取了图信号的多尺度特征，使得图卷积网络中的特征趋于多样化，避免了特征过平滑的问题。具体为

受 到Min 等 人（2020）的启发，Wenkel 等 人（2022）提出了混合图散射模型（hybrid scattering network，Hybrid-GSN），首先通过可学习参数Θ∈Rd×d′将特征映射到新的空间中，通过图卷积与图散射分别提取低通和带通特征，通过更一般的聚合函数fAGGREGATE(·)对各低 通特征和带通特征进行聚合，得到高阶的输入信号特征，即

3.2.2 图散射网络的变型

在传统图散射变换的基础上，后续的工作提出了多种图散射网络的变型来提高图散射网络在图任务上的表现（Min 等，2021；Cheng 等，2022；Tong 等，2022），解决传统图散射网络缺陷（Ioannidis 等，2022），或将图散射网络拓展到更复杂的时空图领域（Pan等，2021）。

1）注意力机制下的图散射网络。GSAN（graph scattering attention network）（Min 等，2021）采 用与Scattering GCN 相似的特征提取结构，同时引入了GAT（Veličković等，2018）中的注意力机制，通过学习各节点的自适应权重来聚合不同尺度下的图散射特征和图卷积特征。GSAN 通过定义注意力机制向量的共享参数a∈R2d（d为输入特征的通道数）来计算各卷积特征和散射变换特征的注意力权重，通过自适应注意力权重融合低通与带通特征，即

式中，C=K+fcard(Ω)为低通特征和带通特征的数量之和，fcard()表示集合中元素的个数，非线性激活σ(·)=fReLU(·)。

2）剪枝图散射变换。由于不同图信号的频谱分布不同，图散射网络中可能出现输出特征接近0 甚至等于0的散射路径。注意到这个问题，Ioannidis等人（2022）对图散射网络进行剪枝来节省计算时间与特征存储空间。对于一条散射路径p及其延伸路径[p，j] (0 ≤j≤J-1)，若路径[p，j]上的散射传递信号能量与上一层传递信号能量的比值小于一个阈值τ，则将路径[p，j]及其延伸路径剪去，具体为

通过去掉不重要的分枝，剪枝图散射变换（pruned graph scattering transform，p-GST）在几乎保持原本表征学习能力的前提下节省了运算时间和特征存储空间。

3）时空图上的图散射变换。ST-GST（spatiotemporal graph scattering transform）（Pan 等，2021）提出了图散射网络在时空图中的表现形式。对于一个输入的时空信号X∈RN×T，在采用空域图和时域图的惰性随机游走矩阵作为图移位算子及其对应的空域小波的情况下，ST-GST 采用二元组来定义散射路径上的一个节点。定义在散射路径上的时空图的散射传递算子为

基于时域与空域上不同尺度小波的组合，时空图的图散射每一层都会散射出Js×Jt个不同的传递信号。在后续工作中，ST-GSTN（Cheng等，2022）引入了p-GST（Ioannidis等，2022）的剪枝思想来提升时空图下图散射网络的运算速度并节省特征存储空间。

4）多尺度的图散射网络。MGST（multi-scale graph scattering transform）（Liu 等，2022）尝试将图进行划分，通过在原图和子图上分别进行图散射变换来学习图的多分辨率下的多尺度特征。MGST 考虑最小的不为0 的特征值对应的特征向量umin在各顶点的正负情况，将原图的点集V划分为V+={vi∈V，umin(vi) ≥ 0}和V-={vi∈V，umin(vi)＜0}两个点集，然后分别保留两个点集内部的边来构建子图G+和G-。通过同样的方法对子图进行再次划分，能够得到一系列节点数更少的子图。MGST 将输入信号分别在原图和一系列子图上进行图散射变换，得到图信号的多分辨率图多尺度特征。

5）自适应图散射网络。上述图散射网络都是基于一组固定的多尺度小波滤波器对输入信号进行图散射变换，在表征学习的灵活性上有一定的局限性。LEGS（leanable geometric scattering）（Tong 等，2021，2022）首次将可学习参数引入图散射网络滤波器的构建中，通过对扩散小波尺度的自适应选取来构建最适用于当前数据集的扩散小波。对于尺度范围{1，2，···，m}，LEGS 采用可学习的尺度筛 选矩 阵F∈RJ×m，具体为

通过softmax 层对每个滤波器采用的图散射尺度进行自适应选取。LEGS 的小波滤波器组的表达式为

对比采用固定扩散小波的传统图散射网络，LEGS 构建的自适应扩散尺度选取滤波器组能更好地应用于频谱分布不同的数据集上，在表征学习任务中具有更好的灵活性。

图散射变换工作的对比与总结如表4 所示。作为一类新型的图卷积技术，图散射网络有一套基于小波的L2(G)空间划分标准，而图散射网络本身的结构（详见图1）有利于产生带通滤波器提取图的中高频信息，且层间非线性也避免了不同散射路径特征重复的问题。因此图散射网络产生的特征趋于多样化，且一般不存在过平滑的问题。

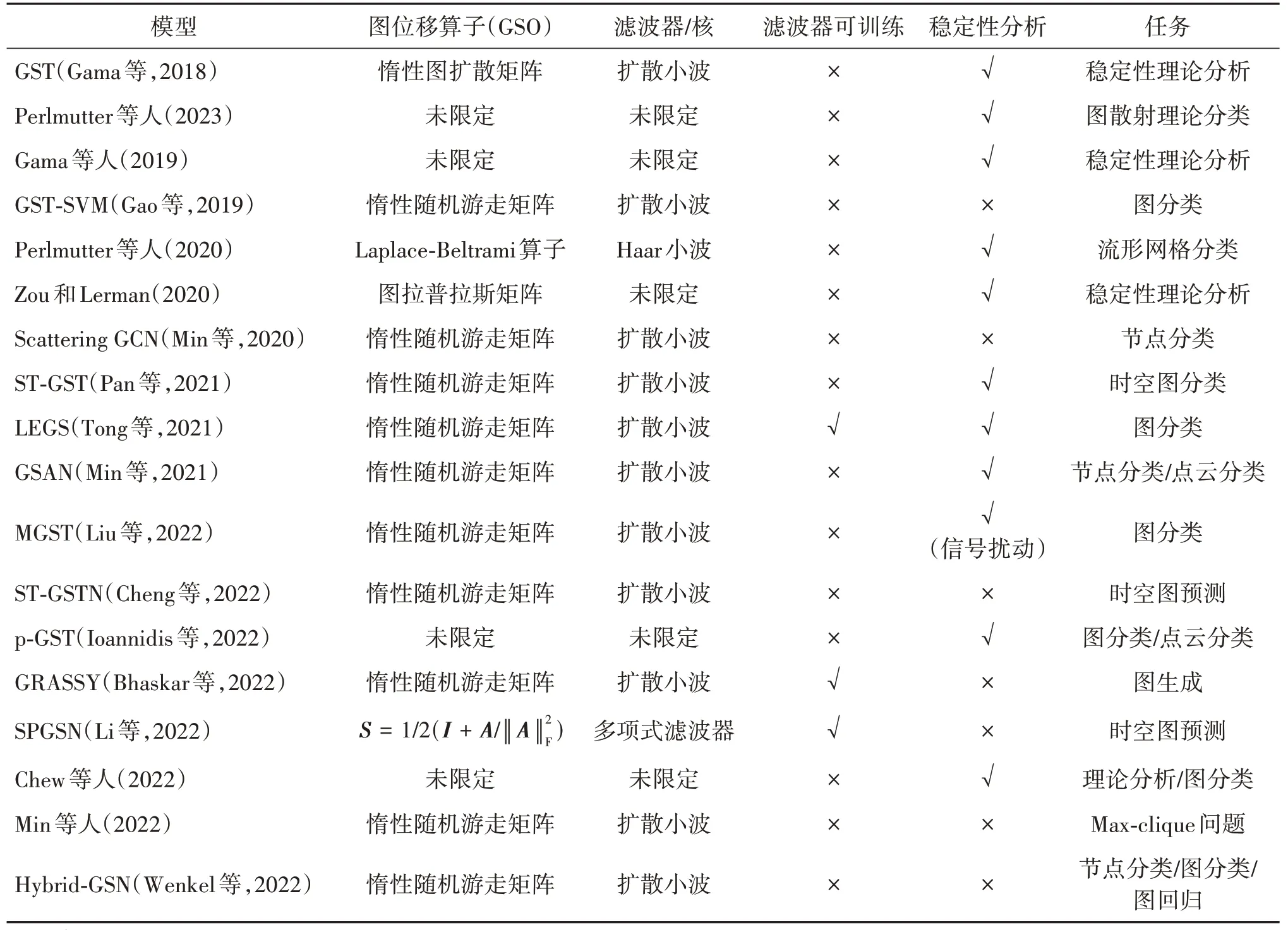
表4 图散射变换工作的对比与总结Table 4 Comparison of works in graph scattering networks field

3.3 图散射的稳定性理论

与图卷积网络不同，由于图散射网络是由面向传统信号的散射网络在图与图信号上的拓展，基于信号处理的图散射网络必须具备良好的对噪声的抗干扰性，即当输入信号或图拓扑受到扰动时，输出的扰动必须局限在一定范围之内。

3.3.1 信号扰动下的稳定性理论

对于图信号x和扰动图信号以及原图G和拓扑扰动下的图，Zou和Lerman（2020）将图散射变换特征的扰动量描述为

即输出的散射变换特征差异量为散射变换输出特征的欧氏距离。

在图散射变换的稳定性分析中，不同工作对于图信号扰动的描述趋于一致。Gama 等人（2018）通过构建图散射变换的框架理论来约束信号扰动下的特征差异，采用作为图移位算子，其特征值分布在［0，1］之间，当特征值最大的绝对值βG＜1 时，此时Ψ={ψj，φJ}构成稳定的框架，即存在与βG相关的常数C(βG)，使得

由于图散射网络中取模的非线性操作并不会改变网络中传递信号的能量，小波的框架理论使得信号扰动下散射特征扰动量存在上限。类似地，Zou和Lerman（2020）提出当小波满足

时，散射网络上下层之间的信号能量满足

即网络中第l层的散射传递能量等于该层图散射网络节点输出特征的能量与第l+1 层的散射传递能量之和。因此，散射传递的信号能量逐层递减，网络中的总能量趋于收敛，因此信号扰动下的输出特征差异也是有界的。

3.3.2 图拓扑扰动下的稳定性理论

相比信号扰动，图散射网络对图拓扑扰动的稳定性是相对热门且困难的课题。与面向传统信号的散射网络不同，图拓扑的扰动会改变将输入信号投射至谱域的基向量，使得频谱分布和每个频率分量的大小与原频谱均有差异。不同工作对图扰动的定义也不相同，因此结论也有所差异。Gama 等人（2018）通过扩散距离（diffusion distance）来定义图的最小距离。将图G与的惰性图扩散矩阵记为和，则有

式中，Π表示置换矩阵（permutation matrix）。将小波分解过程记为Gama 等人（2018）给出了散射传递中小波分解产生的传递信号差异的上界，即

Gao 等人（2019）采用图对齐的方式来衡量图之间的最小距离，通过置换矩阵Π0对扰动图的节点进行重排序，使其图位移算子与原图G的图位移算子S的距离最小，通过误差矩阵ξ来描述S和之间的关系，具体为

对于一组框架下界和上界分别为A和B的小波，有

与Gama 等人（2018）和Gao 等人（2019）采用置换矩阵来定义扰动图与原图间的最小距离不同，Zou和Lerman（2020）采用特征值的最大扰动量以及特征向量之间的最大夹角来定义图的拓扑扰动量。当存在常数C2和C3使得特征值扰动量和特征向量扰动量满足∀l=1，2，···，N，在Zou和Lerman（2020）的小波框架下（A=B=1），此时散射变换特征差异的上界为

式中，C′=3CM(M-2(-1)-2(-1)3(1-M))，C0是衡量图散射网络中能够能量逐层递减比的常数，满足

3.4 图散射网络理论与技术的发展方向

作为一类不可训练的谱域图卷积网络，图散射网络目前的应用和理论发展都还局限在小波框架内。对于不同数据集，可能需要不同的滤波器才能达到最佳的特征提取效果，因此图散射网络的不可训练性一定程度上限制了其表征学习的灵活性。虽然Tong 等人（2021）创造性地引入可学习参数在图散射网络中构建自适应滤波器，但基于尺度筛选的自适应滤波器训练依然基于散射小波框架，且需要在训练前规定尺度筛选范围。过大的范围会导致计算的时间成本上升，过小的范围又会降低滤波器的学习能力和模型的表达能力。另一方面，虽然图散射网络的结构有助于产生多样化的特征输出，但其散射路径随层数呈指数增长的关系也限制了图散射网络的深度。对于较深的图散射网络，表征学习的计算开销往往比较高昂。因此，在目前的应用中，图散射网络的深度大多限制在3～5 层。若在图散射网络中引入层间图池化操作，不仅能够节省计算时间成本，还能提取图的多分辨率特征。然而，图散射网络中还不存在层间图池化的操作，这可能是因为现存的图池化技术无论是基于节点筛选（Zhang 等，2018b；Ying 等，2018；Gao 和Ji，2022）还是基于节点聚类（Von Luxburg，2007；Bruna 等，2014）大多存在边界效应，即在特定条件下原图中极小的拓扑扰动会极大地改变池化后图的拓扑结构，使得图散射网络在后续散射变换中输出截然不同的特征，破坏图散射网络对图拓扑扰动的稳定性。因此，如何在引入图池化的同时保持图散射网络的稳定性是一个具有挑战且意义重大的问题。

在图像与图形的应用层面，目前GCN 已经能够通过对视频进行逐帧构图，进行视觉场景分类（Zhou等，2022b），以及图像和时空图的分类与分割（李占利 等，2020；姚睿 等，2021）。GSN 虽然已经能够适用于静态图（Gao 等，2019）、网格与流形（Perlmutter，2020）和时空图（Cheng 等，2022；Li 等，2022）的分类和预测，但由于时空图下的图散射变换（ST-GST）不同时刻的图结构必须相同，目前依然缺乏采用图散射变换解决视频类数据的相关应用。

在理论方面，目前对图散射网络的理论性分析依然局限在小波框架内。然而，传统散射变换已经取得了突破性的进展。在Mallat（2012）以及Bruna和Mallat（2013）提出散射变换并分析了小波框架下的散射网络的平移不变性和对输入扰动的稳定性后，Wiatowski和Bölcskei（2015）对Mallat的结论进行了推广，采用更一般的李普希茨连续的滤波器组替换了散射网络中的小波滤波器组，最终Wiatowski 和Bölcskei（2018）将Wiatowski 和Bölcskei（2015）中的结论进一步推广完善，将卷积神经网络中面向传统信号的池化（最大池化除外）和更一般的非线性激活引入散射网络中，完善了散射网络在半离散框架下的稳定性理论。另外，图神经网络中的稳定性理论分析也在逐步推进，Gama 等人（2020a，b）和Kenlay等人（2020）构建多项式谱域滤波器并证明了其在谱域图卷积中的稳定性。因此，如何将半离散框架引入图散射网络的稳定性理论分析也是值得研究的问题，对未来图散射变换技术的进一步发展有启发性和指导性作用。

4 结语

对比图卷积网络，图散射网络不仅不存在空域图卷积网络中的过平滑问题，还能通过小波分解输出多样化特征，克服传统谱域图卷积模型表达能力不足的问题。本文对近年来的图卷积网络的技术以及图散射网络的技术发展和理论成果进行归纳，从图卷积网络入手分别介绍了近年来的空域图卷积和谱域图卷积的技术发展，同时借助谱域图卷积引出图散射网络，总结了图散射变换的定义、技术应用和理论发展，对目前图散射网络技术和理论上的缺陷进行了分析，并提出了图散射技术未来可能的研究方向。