多任务的高光谱图像卷积稀疏编码去噪网络

涂坤，熊凤超，傅冠夷蛮，陆建峰

南京理工大学计算机科学与工程学院，南京 210094

0 引言

高光谱图像（hyperspectral images，HSIs）同时采集目标的二维空间信息和一维光谱信息（Xiong 等，2021），可以看做传统彩色图像在波段维进行扩展。由于成像技术、设备误差以及成像环境等因素，采集到的图像在不同波段存在着不同程度噪声。这些噪声对后续的分类、识别和检测等高层次任务具有直接的影响。因此，为了提高高光谱图像实用价值，高光谱图像去噪是后续任务中一个不可或缺的预处理步骤。

高光谱图像是高维数据，由于光谱通道和空间像素之间的强相关性（Zhu 等，2014），干净高光谱图像本质上具有低维结构。针对高光谱图像数学特征，有学者提出基于稀疏表示的高光谱图像去噪方法。假设干净高光谱图像可以由字典中少数基原子线性表达。而噪声由于具有随机性，无法得以表示。噪声图像和重构图像之间的残差即认为是噪声数据。在重构过程中，残差被丢弃，从而达到去噪目的。基于稀疏表示高光谱图像去噪方法的数学形式为

式中，Y是输入的有噪声图像，D是字典，S是稀疏表示系数，是L0正则项，表示非0元素的个数，λ是正则项系数。L0范数对应优化是NP-hard问题，通常替换为其最小凸闭包L1范数。稀疏表示是提取图像结构信息的重要方法，其中字典代表了图像的特征抽取算子，对应稀疏编码代表图像的结构信息。

字典在稀疏表示中起着至关重要的作用。若将字典的原子大小设置为原始图像大小，将面临着高维图像数据带来的维数灾难。因此，Elad 和Aharon（2006）提出K-SVD（K-singular value decomposition）算法。该算法从噪声图像中提取重叠的局部图像块，从大量图像块中自适应地学习字典。根据学习到的字典，分别对每个图像块稀疏表示，最后通过平均每个块之间的重叠像素全局重构图像。为了保留高光谱图像波段间的光谱信息，Xiong等人（2022）采用在多波段间共享稀疏系数的方式，提出了多任务稀疏去噪模型（multitask sparse neural network，MTSNN），但该方法仍是将图像划分为重叠的局部图像块，基于图像块学习字典。基于图像块的稀疏表示方法忽略了图像块之间的空间关联和图像的平移不变性（Sreter和Giryes，2018），去噪能力有限。

卷积稀 疏编码（convolutional sparse coding，CSC）将基于图像块稀疏表示中的原子替换为具有平移不变性质的卷积核，用多个卷积核的集合作为字典（Choudhury 等，2017；Simon 和Elad，2019；Zheng等，2021）。多个卷积核可以通过展平拼接为一个包含带状循环矩阵的全局平移不变字典。每个循环矩阵是通过将单个列移位到所有可能的移位构建，在数学上通过卷积实现。一方面，卷积稀疏编码具有天然的平移不变性；另一方面其可以将整幅图像作为输入，避免了图像块的划分，更好地保留图像结构信息。其数学形式为

式中，⊗代表卷积操作。与式（1）不同之处在于，D=是由M个卷积核构成的字典，对应输入图像Y由卷积字典D得到的M个稀疏系数的集合。由于避免了图像块的划分可以更好地保留图像结构，卷积稀疏编码在图像超分辨率和图像融合等任务中取得了显著效果（Zisselman 等，2019；Deng和Dragotti，2021）。

传统卷积稀疏编码主要应用于二维图像，在高光谱图像去噪领域研究仍比较少。一种方法是高光谱图像每个波段可以看做是二维灰度图像，卷积稀疏编码可以分波段对高光谱图像建模。但高光谱图像是三维数据，波段之间存在显著的关联关系。分波段应用卷积稀疏编码会不可避免地破坏高光谱图像波段之间关联性。另一种方法是将传统的2D 卷积替换为3D卷积，实现高光谱数据局部空间—光谱结构建模。高光谱图像每个波段刻画目标在各个波长上的响应，即各个波段描述同一个目标，这意味着高光谱图像波段之间关联关系具有全局性。而3D卷积只能利用高光谱数据波段之间局部关联，无法实现高光谱数据波段间全局建模。

为了解决上述问题，本文提出多任务卷积稀疏表示模型处理高光谱图像去噪问题。该模型将单波段去噪视为单任务卷积稀疏表示，将多波段去噪视为多任务卷积稀疏表示，并通过共享稀疏编码对多个任务之间的波段关系进行全局建模，从而实现波段间全局信息共享。共享卷积稀疏编码可以实现对不同噪声水平波段联合去噪，从而提高模型去噪能力。在迭代软阈值收缩算法框架下，本文推导了其迭代优化求解算法。为了避免迭代耗时和超参数调优问题，如图1 所示，本文通过深度展开的方式将多任务卷积稀疏表示模型转化为一个端到端的可学习的多任务卷积稀疏编码网络（multitask convolutional sparse coding network，MTCSC-Net）。该网络包括编码层和解码层。编码层提取输入图像的稀疏特征。解码层从稀疏特征中恢复干净高光谱图像。与传统基于优化的去噪方法不同，MTCSC-Net 采用数据驱动方式自适应地学习所有参数。网络训练完成后，高光谱图像去噪任务变为有限次网络前向传播过程，具有很强的算法运行效率。MTCSC-Net 的网络架构由多任务卷积稀疏编码模型得到。内在的物理模型使得其相比于“黑盒”神经网络具有更强的可解释性。

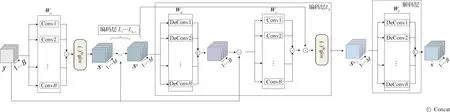
图1 MTCSC-Net网络结构图Fig.1 The architecture of MTCSC-Net

本文主要贡献归纳如下：1）提出多任务卷积稀疏编码模型，通过在不同波段间共享卷积稀疏系数，实现高光谱图像的空间—光谱关联，有效地提升了模型去噪能力；2）利用深度展开技术，将多任务卷积稀疏编码模型转化为一种端到端的多任务卷积稀疏编码网络，具有更强的可解释性、学习能力和去噪能力；3）大量的对比实验证明本文方法具有领先的高光谱图像去噪效果。

1 相关工作

1.1 基于模型的高光谱图像去噪方法

高光谱图像作为自然图像具有空间和光谱冗余性。基于模型的去噪方法通常利用低秩和稀疏表示方法对干净高光谱数据建模以去除噪声。BM4D（block matching and 4D filtering）（Maggioni等，2013）将2D 图像块拓展为3D 的体素数据块，利用非局部体素之间的联合稀疏性对高光谱图像去噪。类似地，TDL（tensor dictionary learning）（Peng 等，2014）利用组图像块之间的联合稀疏性约束创建了非局部张量字典学习模型，令相似的图像块共享字典。MTSNMF（multitask sparse nonnegative matrix factorization）（Ye 等，2015）引入多任务的概念，通过在多波段间共享系数矩阵建立了多任务稀疏非负矩阵分解模型。LLRT（hyper-Laplacian regularized unidirectional low-rank tensor）（Chang 等，2017）利用非局部自相似性的低秩特性提出了单向低秩张量恢复模型。3DLogTNN（three-directional log-based tensor nuclear norm）（Zheng 等，2020）对张量奇异值分解进行拓展，并引入了3 方向基于对数的张量核范数进行去噪。龙珍等人（2023）利用高光谱图像线性张量子空间对应系数的低秩结构，提出了具有正交向量的结构低秩矩阵向量张量分解算法。基于稀疏和低秩方法的问题在于他们通常需要将三维高光谱数据划分为一系列的小图像块进行表示。这种处理机制不可避免地破坏高光谱数据的空间结构特性。此外，尽管模型方法通常具有良好的可解释性与泛化能力，但比较依赖先验知识和人工设定超参数。

1.2 基于深度学习的高光谱图像去噪方法

随着深度学习的发展，纯数据驱动的思想逐渐流行起来。在高光谱图像去噪领域中表现为通过深度卷积神经网络捕获具有高度代表性的层次特征和上下文信息，以提高图像质量。为了保留更多的边缘信息和纹理细节，吴从中等人（2018）引入了深度残差网络。为了利用光谱信息，Yuan 等人（2019）将噪声波段及其相邻波段输入残差卷积神经网络HSID-CNN（HSI denoising with a deep CNN），然后逐波段执行去噪。为了更好地模拟高光谱图像的三维结构，Dong 等人（2019）将U-Net 中的2D 卷积替换为3D 卷积，构建了3D U-Net 以同时提取空间和光谱特征。Wei 等人（2021）设计的QRNN3D（3D quasirecurrent neural network）使用两组3D 卷积挖掘波段上的全局相关性以进行去噪。但传统的深度学习方法通常面临着缺乏先验知识指导、依赖大量训练数据以及泛化能力弱的问题。

2 本文算法

在高光谱图像中，图像的噪声形式主要表现为泊松噪声、条形噪声以及高斯噪声等混合噪声。其中高斯噪声是最常见的噪声，因此本文考虑高斯噪声。假设X∈Rh×w×B是一个波段数为B、长为h、宽为w的高光谱图像，噪声大小为N∈Rh×w×B，观察到的噪声图像Y∈Rh×w×B对应的退化模型为

从Y中得到X是一个欠定问题，X的先验知识对问题求解起着非常关键的作用。考虑到卷积稀疏表示在图像结构保留方面的优势，本文采用卷积稀疏先验对X进行建模。

2.1 多任务卷积稀疏表示

给定第b波段图像Xb∈Rh×w，根据卷积稀疏表示模型，其可以由卷积字典中卷积核稀疏表示而成，对应的数学表达式为

如果将单波段的去噪任务看做单任务卷积稀疏表示问题，多波段的去噪任务则为多任务卷积稀疏表示问题。高光谱数据是三维数据，不同波段刻画了目标在相应波长响应，即不同波段之间存在强结构性关联，可以通过共享稀疏编码实现。式（4）对高光谱图像分波段进行卷积稀疏表示，没有考虑波段之间的关联。如图2 所示，本文要求所有波段之间共享卷积稀疏编码以刻画波段间关联关系。多任务卷积稀疏编码的数学表达式为

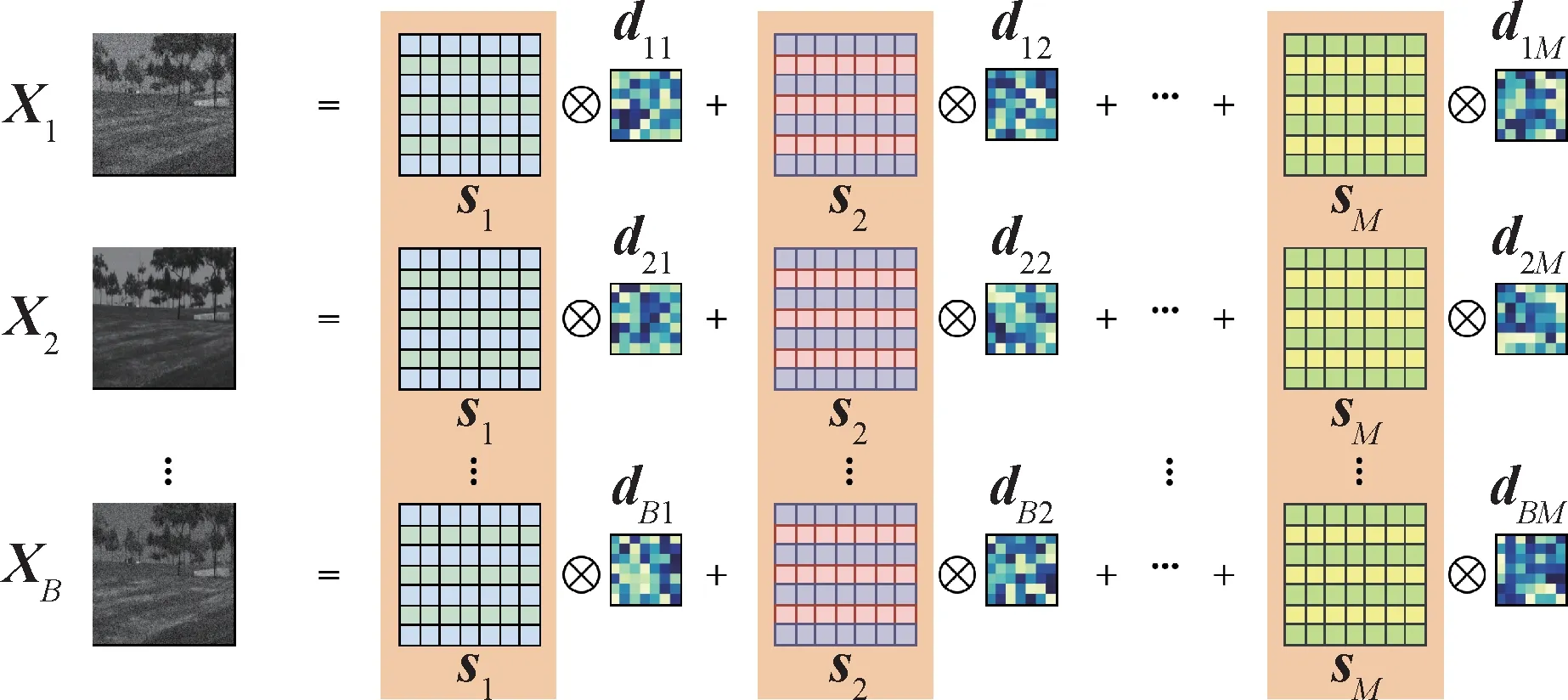
图2 多任务卷积稀疏表示Fig.2 Multitask convolutional sparse coding

2.2 多任务卷积稀疏网络

卷积稀疏编码的求解主要包括交替方向乘子法（alternating direction method of multipliers，ADMM）、迭代软阈值收缩（iterative soft-thresholding algorithm，ISTA）和快速迭代阈值收缩（fast iterative shrinkage thresholding algorithm，FISTA）（Garcia-Cardona 和Wohlberg，2018）。考虑到ISTA 算法的简洁性，本文选取ISTA 方法进行求解推导出求解公式。当字典已知时，式（6）可以由ISTA 算法求解，对应的迭代求解式为

式中，C为步长，soft(·)是软阈值收缩算子，其定义为softθ(x)=sign(x) · max(|x|-θ，0)。经 过K次迭代得到SK，去噪后的图像，其中第b波段图像为

在基于模型的方法中，式（7）的求解需要大量耗时的迭代过程，并且需要手工设置λ。另外式（7）并没有考虑数据，只是对图像的物理结构信息进行建模。现实图像内容的复杂性和噪声复杂性导致式（7）中的建模方式并不能很精确地建模高光谱图像。本文将式（7）的求解过程看做神经网络前向传播过程，通过引入一些可学习变量，采用深度展开技术将算法迭代转化为可学习神经网络。相应式（7）可以看做是深度编码过程，而式（8）看做深度解码过程。具体而言，引入可学习参数Wd=[D1，…，DB]，替代原公式中的部分参数，将式（7）和式（8）转换为如下多任务卷积稀疏编码网络（MTCSC-Net），具体为

式中，softθk(·)表示软阈值收缩算子对应网络中的非线性激活函数，可以通过ReLU(s-θk) -ReLU(-s-θk)实现，其阈值θk=λk/C也是可学习参数之一。通过网络的反向传播进行参数更新可以避免模型方法中手工调参过程。式（9）通过一些神经网络参数替换式（7）中的字典，将相应的数值优化转化为可学习神经网络，通过数据驱动方式学习到高光谱图像的建模方法。一方面，式（7）已经提供了一些图像内容建模的先验信息，可以简化深度学习建模的难度；另一方面，数据驱动学习可以增强建模能力，降低图像建模难度。

给定N个样本，MTCSC-Net 的损失函数定义为输出去噪图像与对应参考图像之间的均方误差，即

2.3 与CSC-Net之间的关系

CSC-Net（convolutional sparse coding network）（Simon和Elad，2019）采用跨步卷积实现卷积稀疏编码，该模型旨在对灰度图像进行去噪。高光谱图像可以看做由不同波段灰度图像在光谱维度堆叠而成。因此，传统的灰度图像去噪算法如CSC-Net 可以分波段对高光谱图像去噪。此时，单个波段图像的去噪可视为单任务卷积稀疏表示。分波段的单任务卷积稀疏表示忽略了波段之间的关联性，往往产生较差的去噪效果。MTCSC-Net通过在不同波段图像之间共享卷积稀疏表示系数，实现波段之间关联建模，可以同时利用不同波段空间稀疏性和波段之间信息，具有更强的去噪能力。

3 实验结果

使用两个仿真数据集和一个真实数据集验证所提出算法有效性。

3.1 实验设置

3.1.1 网络实现

本文设置深度展开层数K=7，每个波段字典原子个数M=256，卷积核大小为9 × 9，卷积核步长为5。实验中分别分析这些参数对去噪性能的影响。实验代码通过PyTorch 实现，其中Wd和Wf采用卷积实现，而We采用转置卷积实现。实验中采用Adam优化器对目标函数优化，迭代次数为200 轮。算法初始 学习率为5 × 10-4，每 隔80 次以0.35 倍数下降。

3.1.2 实验数据

采用仿真实验和真实实验对算法进行测试。在仿真实验中，用ICVL（http：//icvl.cs.bgu.ac.il/hyperspectral/）和CAVE（Columbia Imaging and Vision Laboratory）（https：//cave.cs.columbia.edu/repository/Multispectral/）高光谱图像数据集评估算法性能。ICVL 数据集包括100 幅图像构成的训练集，50 幅图像构成的测试集。每幅图像原始尺寸为1 392 × 1 300 × 31。在训练过程中，选取尺寸为64 × 64 × 31的子图像对网络进行训练；在测试过程中，选取尺寸为512 × 512 × 31 的子图像用于测试。在CAVE 数据集中，训练集和测试集分别包括20 幅和12 幅图像，图像尺寸为512 × 512 × 31。在仿真实验里，对干净高光谱图像每个波段加入不同标准差的加性高斯噪声以产生噪声—干净图像对。为了拓展训练样本并且避免对数据集的过拟合，本文方法在数据预处理中添加了缩放、水平翻转和垂直翻转等操作进行数据增强。其中，标准差σ在［0，15］、［0，55］和［0，95］ 这3 个范围。最后，选用了Urban 数据测试对比算法在真实数据上的性能。

3.1.3 算法指标

本文使用峰值信噪比（peak signal-to-noise ratio，PSNR）（Horé 和Ziou，2010）、结构相似度（structural similarity，SSIM）（Wang 等，2004）和光谱角（spectral angle mapper，SAM）（Fang 等，2013）作为评测指标，定量评价各个算法的去噪效果。

3.2 与CSC-Net算法比较

在本实验里，为了与CSC-Net 进行比较，逐波段采用CSC-Net 对高光谱图像去噪。为了实验公平性，针对不同标准差的加性高斯噪声重新训练了CSC-Net。具体地，在σ∈[0，95]中，分别训练了σ∈{5，10，…，90，95}等19 个模型。在验证去噪结果时读取当前高光谱图像波段的噪声强度，按噪声强度所在区间调取相应去噪模型进行测试。表1 和表2 展示了CSC-Net 和MTCSC-Net 在不同噪声程度下的去噪效果。可以看出，由于有效地利用了高光谱图像波段之间全局关联性，MTCSC-Net 算法性能远超过CSC-Net。

表1 本文方法与CSC-Net在ICVL数据集的性能比较Table 1 Comparison of performance on ICVL dataset between CSC-Net and MTCSC-Net

表2 本文方法与CSC-Net在 CAVE数据集的性能比较Table 2 Comparison of performance on CAVE dataset between CSC-Net and MTCSC-Net

3.3 与其他算法的对比实验

将MTCSC-Net 与其他8 个方法在IVCL、CAVE、Urban 数据集上分别进行比较。对比方法包括基于稀疏的传统算法，如BM4D（Maggioni 等，2013）、TDL（Peng 等，2014）、MTSNMF（Ye 等，2015），基于低秩的方法，如LLRT（Chang等，2017）、3DLogTNN（Zheng等，2020）以及基于深度学习的算法，如SDeCNN（Maffei 等，2020）、QRNN3D（Wei 等，2021）、MTSNN（Xiong等，2022）。

3.3.1 ICVL数据集实验结果

表3 显示了不同方法在ICVL 数据集上的表现。可以看到，传统的稀疏表示方法在噪声程度较低的情况下（σ∈[0，15]）表现较深度学习方法更好，但噪声比较复杂的情况下，基于深度学习的方法表现更好。这是因为在噪声强度大的情况下，精确的物理模型构建存在很大困难。传统方法中手工选取的先验知识存在一定局限性，同时难以设置合适的超参数。而深度学习方法具有强大的表征能力，可以以数据驱动的方式对高光谱图像进行更有效的建模，取得更好的实验效果。对比QRNN3D，本文方法在各个程度噪声下的去噪效果都有提升。以PSNR为例，相应增加幅度分别为4.06 dB（噪声范围σ∈[0，15]）、2.39 dB（噪声范 围σ∈[0，55]）、3.31 dB（噪声范围σ∈[0，95]）。对比MTSNN，其需要提前训练字典对网络进行初始化，而本文无需提前训练字典，直接采用随机初始化，与之相比，本文PSNR提升0.64 dB（噪声范围σ∈[0，95]）。

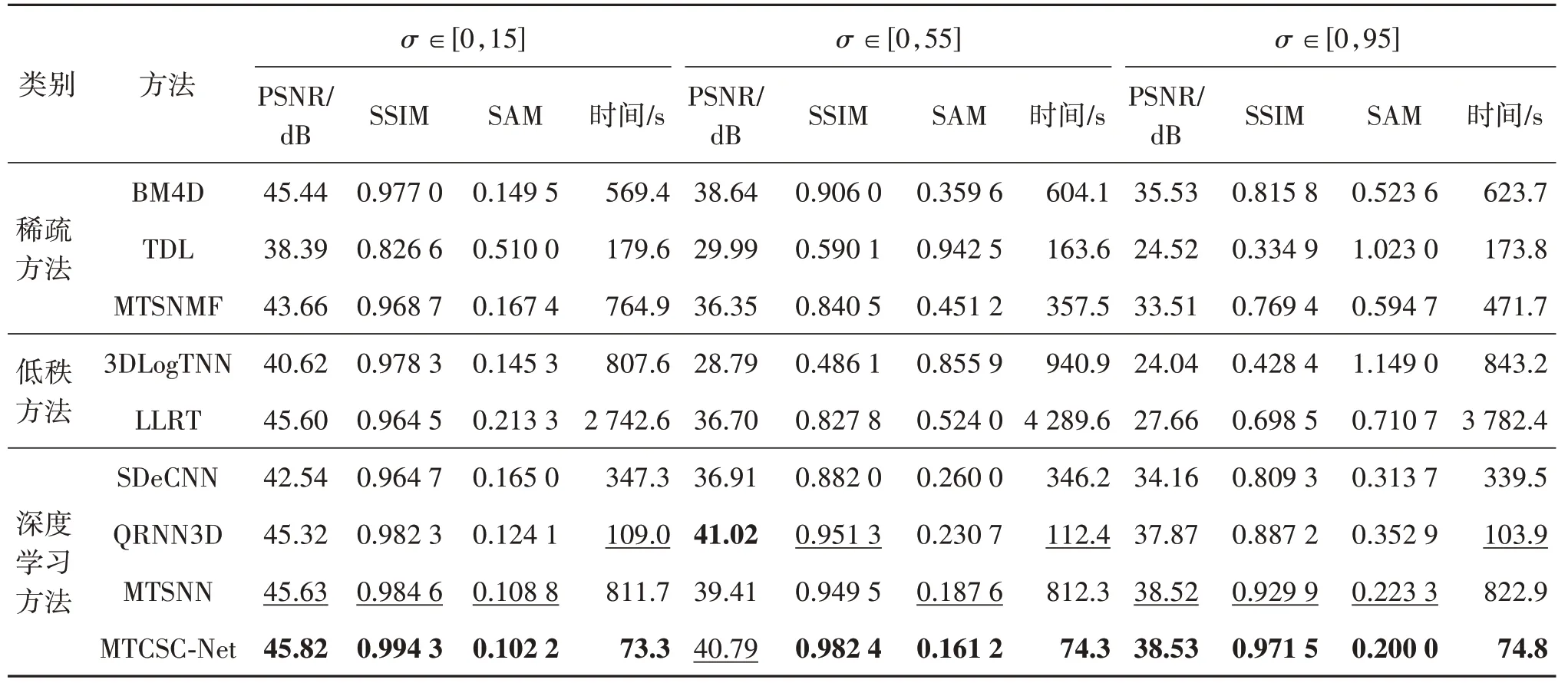
表3 不同方法在ICVL数据集上不同噪声水平下的去噪效果对比Table 3 Comparison of denoising effect under several noise levels on ICVL dataset among different methods

图3 显示了不同方法在ICVL 数据集上ulm_0328-1118 图像的去噪效果。其中，噪声标准差为［0，95］，伪彩色图像通过结合波段6、15 和25 生成。可以看出，BM4D 和LLRT 丢失了大量的图像细节，TDL、MTSNMF、3DLogTNN和SDeCNN仍有明显噪声未去除。本文方法的去噪结果保留了图像的细节信息，并无明显噪声遗留，去噪质量得到了显著提升。

图3 ICVL数据集中图像ulm_0328-1118的去噪结果Fig.3 Denoising results for the ulm_0328-1118 image in the ICVL dataset（（a）clean image；（b）noisy image；（c）BM4D；（d）TDL；（e）MTSNMF；（f）3DLogTNN；（g）LLRT；（h）SDeCNN；（i）QRNN3D；（j）MTSNN；（k）MTCSC-Net）

图4 显示了高光谱图像ulm_0328-1118 中像素（201，201）的光谱去噪结果。从图4 中各方法去噪后的高光谱图像光谱曲线可以看出，本文方法成功地去除了各波段不同程度的噪声，获得与参考光谱一致的曲线。

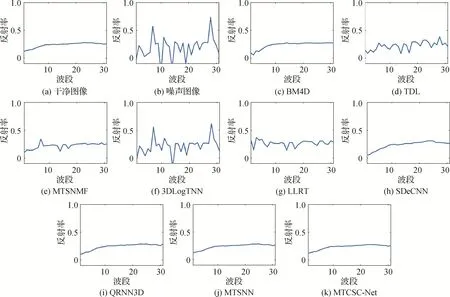
图4 高光谱图像ulm_0328-1118中点（201，201）的光谱去噪结果Fig.4 Denoising results of pixel（201，201）in the ulm_0328-1118 HSI（（a）clean image；（b）noisy image；（c）BM4D；（d）TDL；（e）MTSNMF；（f）3DLogTNN；（g）LLRT；（h）SDeCNN；（i）QRNN3D；（j）MTSNN；（k）MTCSC-Net）

3.3.2 CAVE数据集实验结果

表4 显示了不同方法在CAVE 数据集上的实验对比结果，其中基于深度学习的方法都进行了重新训练。与ICVL数据集结果相似，深度学习方法得益于强大的表征能力和从数据中学习的能力，在噪声比较大的时候取得了更好的去噪效果。与MTSNN相比，本文方法PSNR 提升1.38 dB（噪声范围σ∈ [0，55]），具有更强的去噪能力，也证明了本文方法的有效性。

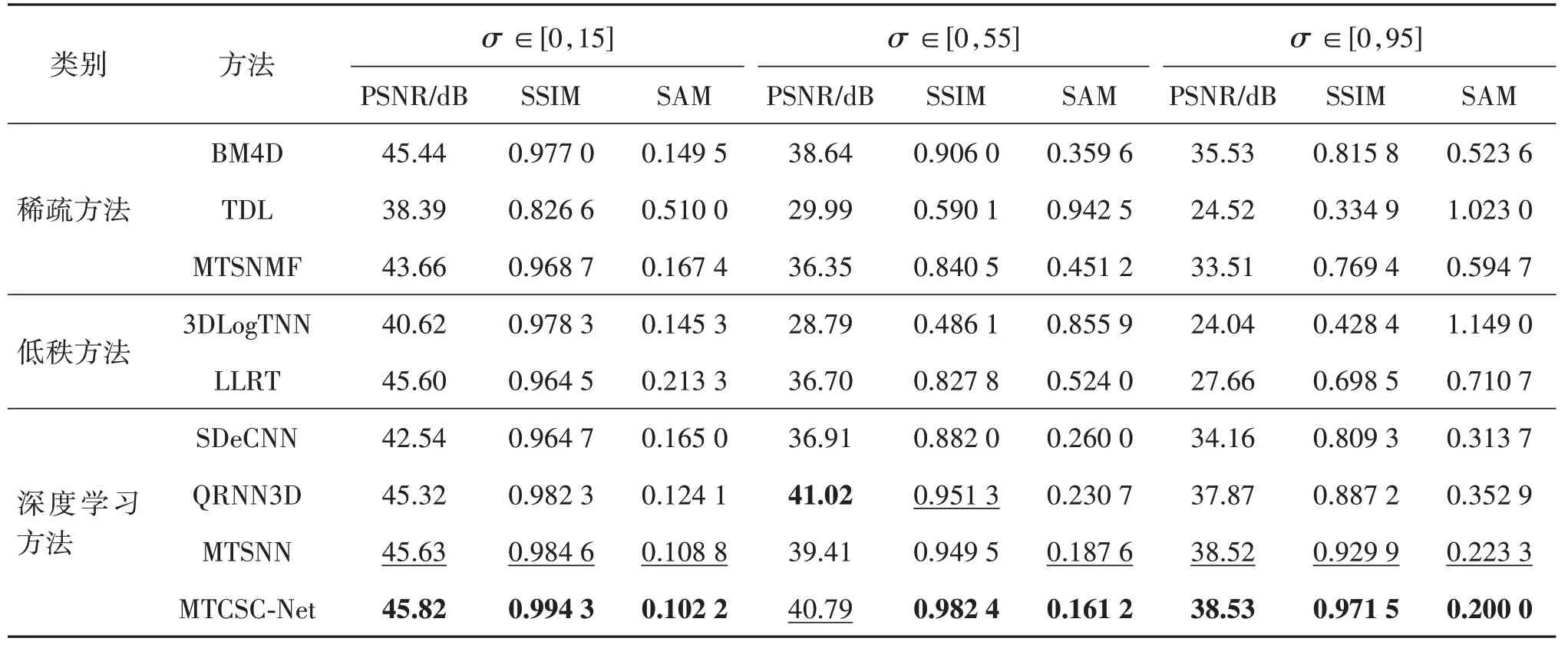
表4 不同方法在CAVE数据集上不同噪声水平下的去噪效果对比Table 4 Comparison of denoising effect under several noise levels on CAVE dataset among different methods

3.3.3 Urban数据集实验结果

除了仿真数据，本文还在真实数据Urban 上进行测试，以证明MTCSC-Net 的泛化能力。Urban 数据光谱范围为0.4～2.5 μm，共210 个波段，每个波段图像为307 × 307 像素。由于真实场景中没有与Urban 数据对应的训练集，直接用在ICVL 数据集上训练的模型进行测试。所有算法的可视化结果如图5 所示，其中伪彩色图像通过结合波段3、108、208 生成。可以看出，面对真实图像中的复杂噪声，MTCSC-Net 利用波段间关联信息进行去噪，去除了图像中的噪声，得到了较为干净的去噪图像，同时保留了图像中的细节信息。图6 显示了Urban 数据集点（120，150）的光谱去噪结果。

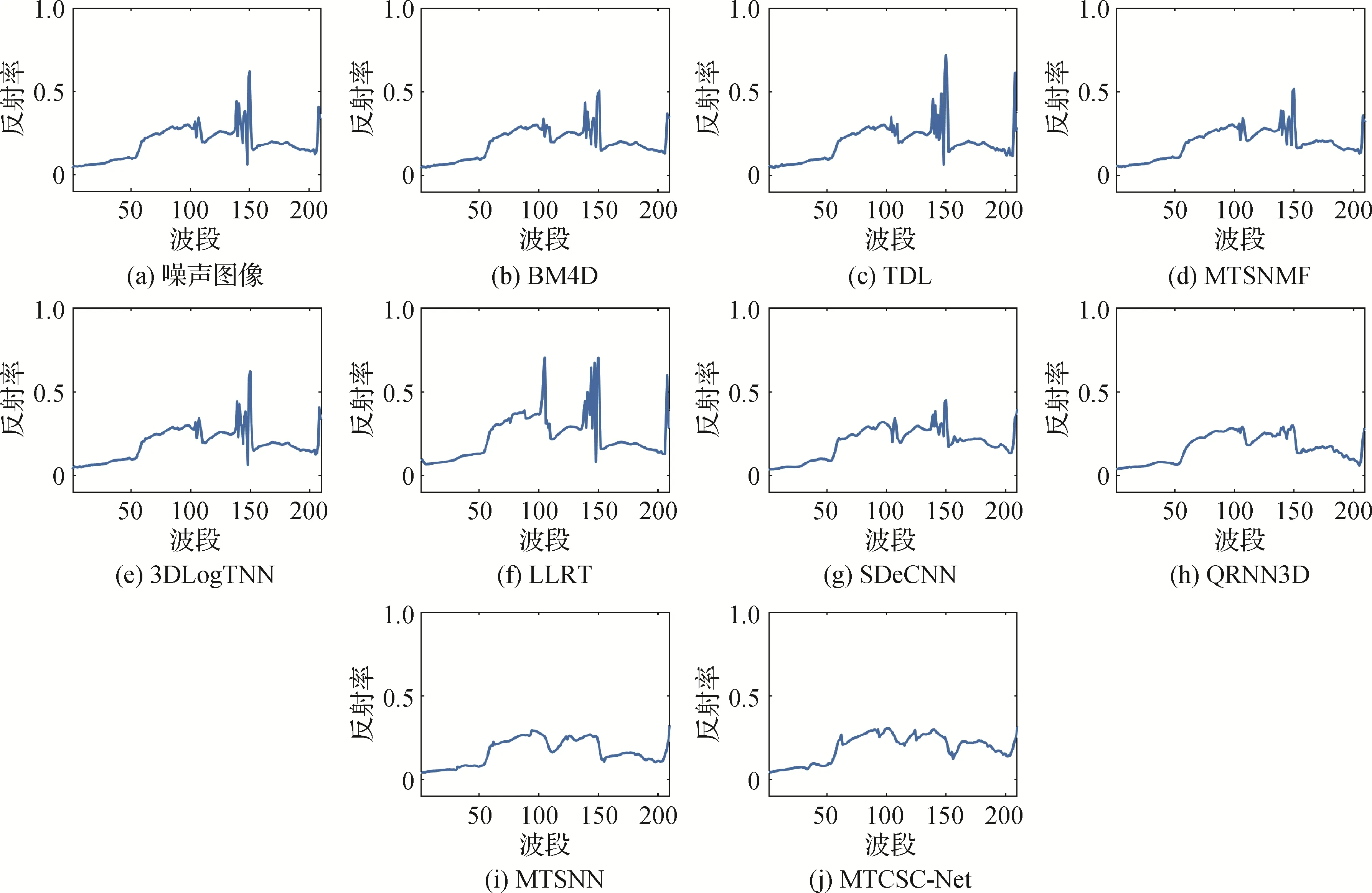
图6 Urban数据集中点（120，150）的光谱去噪结果Fig.6 Denoising results of pixel（120，150）in the Urban HIS（（a）noisy image；（b）BM4D；（c）TDL；（d）MTSNMF；（e）3DLogTNN；（f）LLRT；（g）SDeCNN；（h）QRNN3D；（i）MTSNN；（j）MTCSC-Net）

3.4 卷积字典分析

网络中的卷积核代表了学习到的字典，图7展示了当卷积核大小为9 × 9、个数为256时，网络学习到的第1波段和第22波段所对应的字典。针对每一个波段，字典中的卷积核与图像的边缘等局部信息有关，这表明网络学习到了高光谱图像的局部空间关系。波段1 和波段22 学习到的字典存在一定差异性，这是因为不同波段图像对应目标在不同波长的响应，具有视觉的差异性。网络通过学习到不同波段的差异性字典，将不同波段映射到同一个空间中，以抽取共享的稀疏结构信息，实现全局光谱关系建模。

3.5 网络分析

本节分析字典中卷积核（原子）的个数（M）、卷积核的大小（size）、卷积核的步长（stride）和深度展开的层数（K）对MTCSC-Net算法去噪性能的影响。

3.5.1 卷积核个数的影响

卷积稀疏表示通过卷积核与稀疏表示系数的卷积和重构去噪图像。字典中卷积核个数直接影响模型表达能力的强弱。增大字典大小可以使得网络得到更强的表达能力，但过度增加字典中卷积核数目会使得网络参数过大，从而容易过拟合，反而会降低网络性能。本文对不同卷积核个数对去噪性能的影响进行比较，如表5 所示，最终发现字典原子个数为256时能取得最好的效果。

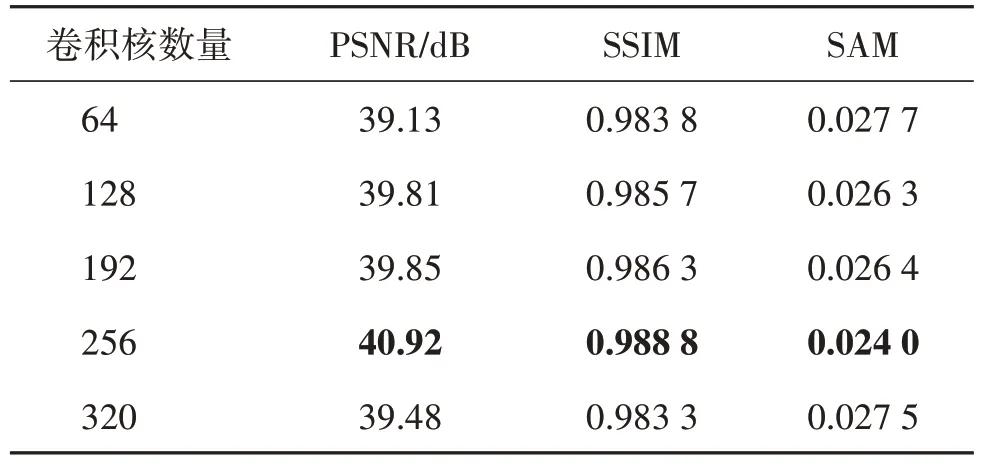
表5 不同卷积核个数对去噪性能的影响Table 5 The impact of the number of convolutional kernels on the denoising performance

3.5.2 卷积核尺寸的影响

一个卷积核对应字典中的一个原子，同时卷积核大小影响着网络中感受野的大小。过小的卷积核无法有效提取图像中的空间信息，过大的卷积核不利于提取局部信息，因此过小或过大的卷积核都会导致去噪效果的下降。如表6 所示，当卷积核尺寸为9时能取得最好的去噪效果。

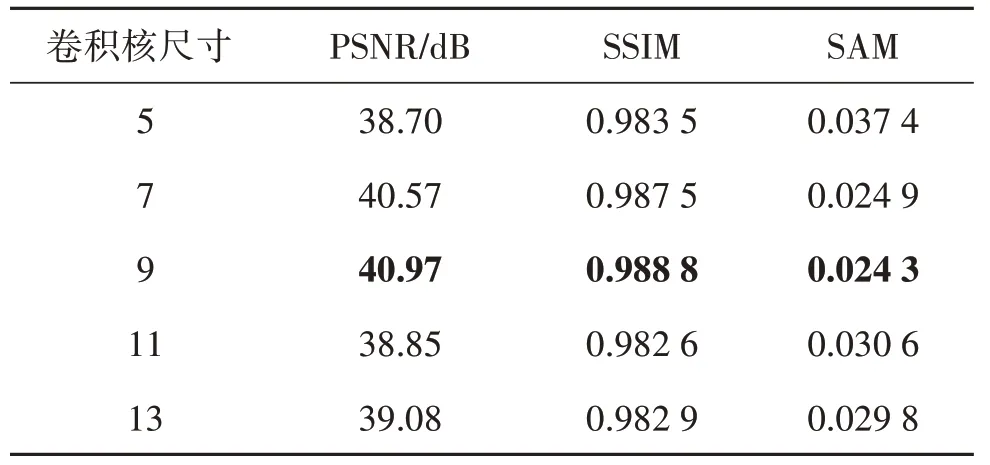
表6 不同卷积核尺寸对去噪性能的影响Table 6 The impact of the size of convolutional kernels on the denoising performance

3.5.3 卷积核步长的影响

过小的步长会导致相邻卷积操作感受野之间重复区域过大，局部图像重复采样；但过大的步长会丢失图像中相邻像素间的空间信息，不利于图像重构。如表7 所示，在卷积核大小为9 的情况下，将步长设置为5能取得最佳效果。

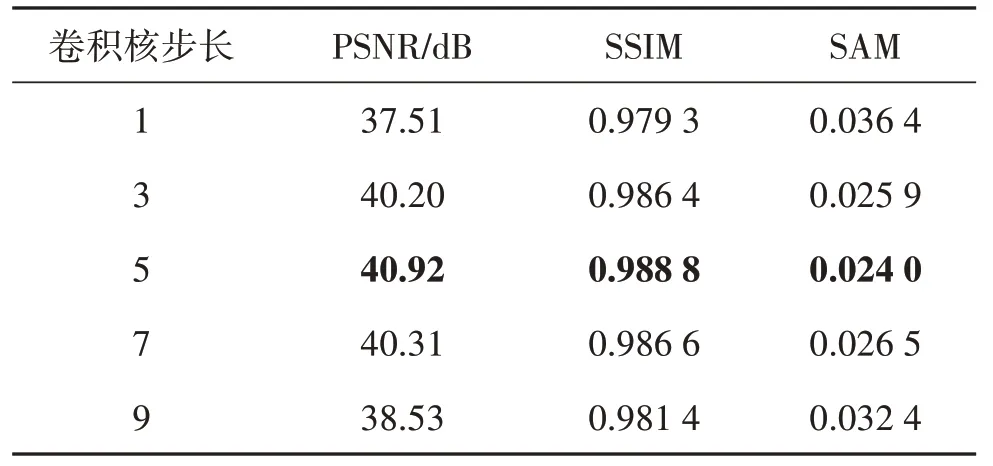
表7 卷积核步长对去噪性能的影响Table 7 The impact of the stride of convolutional kernels on the denoising performance

3.5.4 深度展开层数的影响

MTCSC-Net前向传播过程可以与卷积稀疏编码过程对应。如表8 所示，更大的展开层数能取得更好的结果，但随着层数的增加，网络参数之间依赖程度增加，学习难度亦随之增加，效果随之下降。当展开层数为7时算法能取得最好的效果。

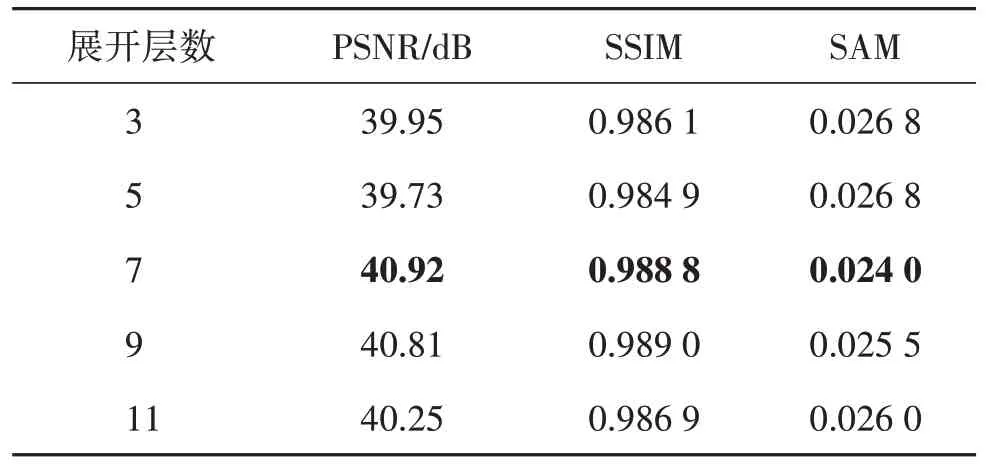
表8 展开层数对去噪性能的影响Table 8 The impact of the number of unfolding layers on the denoising performance

4 结论

针对高光谱图像的波段间结构特点和传统基于图像块划分的稀疏表示去噪方法对图像的整体信息利用较差的问题，本文提出一种基于多任务卷积稀疏编码高光谱图像去噪模型。该模型通过多任务的方式对不同波段的高光谱图像进行去噪，通过在不同波段间共享卷积稀疏编码系数，实现不同波段之间信息联合利用，有效地提升了模型表达能力。此外，采用深度展开技术将基于迭代软阈值收缩算法的求解过程转化为端到端可学习深度神经网络。该网络融合模型方法和数据驱动深度学习方法优势，相较于传统模型方法和单一数据驱动深度学习方法具有更强的去噪能力。大量实验证明了该方法可以有效利用高光谱图像的空间—光谱关联，在高光谱图像去噪任务中取得了优秀的效果。

在未来的工作中，将尝试引入更多的高光谱图像本身的数据特征如低秩结构进行建模，再通过深度网络的方法实现，从而更好地利用模型驱动和数据驱动方法的优点，提升高光谱图像去噪效果。