几何联合分段亮度的线阵图像配准

房磊，史泽林*，刘云鹏，李晨曦，赵恩波，张英迪

1.东北大学机器人科学与工程学院，沈阳 110169；2.中国科学院光电信息处理重点研究室，沈阳 110016；3.中国科学院沈阳自动化研究所，沈阳 110016；4.中国科学院机器人与智能制造创新研究院，沈阳 110169

0 引言

在机器视觉领域，图像配准是一个非常重要的研究课题，其目的是找到两幅图像间最优的几何变换，使得它们在几何上完全对齐（Baker 和Matthews，2004）。图像配准消除了由不同视角下相机成像时目标在图像上产生的几何差异，是许多视觉应用中的一个基本过程，如图像融合（Li 等，2017）、图像跟踪（Alismail 等，2017）和医学图像分析（马露凡 等，2021）等。图像配准需要选择一个合适的几何变换模型描述待配准两幅图像间的几何变换关系，常用于表达面阵图像几何变换关系的模型包括（Zhang等，2020）：平移变换、刚体变换、相似变换、仿射变换和投影变换等。确定描述两幅配准图像间的几何变换关系后，传统方法中可采用基于图像特征点的配准方法（贾迪 等，2019；Li 等，2020）或直接配准方法（Chen 等，2019）计算变换模型中的相关参数；随着深度学习技术的发展，以卷积神经网络提取特征点的半传统半深度方法（Yang 等，2018）和端到端深度学习方法（Rocco 等，2017）也广泛应用于寻求待配准图像间的最佳几何变换关系。

随着线阵相机的广泛使用，线阵图像的配准在工程领域有着重要的应用。在航空航天领域（Storey等，2004；Iwasaki 和Fujisada，2005），线阵相机相对于被采集的目标运动，所拍摄的线阵图像称为遥感图像。Murphy 等人（2016）针对小波配准时初始条件不具备鲁棒性，提出了Shearlet 特征，并联合小波特征优化得到配准图像的仿射变换参数。Ye 等人（2017）设计了一种定向相位一致性直方图特征描述符，并采用仿射变换模型实现了多模态遥感图像的配准。Erives 和Fitzgerald（2005）采用相位相关法对空间或机载平台的非同时遥感图像配准，纠正了图像间旋转、平移和尺度变化。陈颖等人（2021）提出了参数合成的空间变换网络，对遥感图像进行双向一致性仿射变换配准，提高了深度学习模型配准的可靠性和准确性。在轨道交通领域，铁路运输安全问题受到了越来越多的关注（Xu 等，2015；Liu 等，2016）。为了监测列车运行时的情况，相关部门研发了基于线阵相机的列车图像采集系统（the trouble of moving electric multiple units detection system，TEDS）（赵冰 等，2019；周雯 等，2019）。Lu 等人（2018）忽略了不同站点的线阵相机位姿不同，而仅采用平移变换关系对线阵图像进行配准，通过图像减法比对对齐的列车图像，实现列车运行时的安全监测。Lu 和Liu（2016）专注于列车的开口销部件丢失检测，采用多尺度金字塔的模板匹配定位策略，同样忽略了线阵相机位姿不同，而仅采用平移变换模型表达两幅线阵图像的几何变换关系。

目前，线阵图像在配准时仍采用面阵图像的几何变换模型。在遥感领域，线阵相机成像时传感器的高度及搭载平台位置与姿态的变化会导致遥感图像中像素相对于地面目标的实际位置发生扭曲、拉伸和偏移等几何畸变。直接使用这些畸变图像不能满足实际应用的要求，所以几何校正是原始卫星图像数据预处理的关键步骤之一。通过一定量的地面控制点、成像区域的数字地形模型以及传感器的详细姿态，可以进行严格的校正，从卫星拍摄的原始图像中生成正像（Liu，2006；Laliberte 等，2011）。正射校正不仅消除了遥感图像的几何畸变，同时也将不同平台、不同时间相机成像时的视角校正到平行于目标成像，使得遥感图像配准时采用最为简单的平移变换模型或刚体变换模型。在可控的工业应用场景中，线阵相机的传感器平面与被成像目标平行并与运动方向垂直（Steger 等，2018）。在这种情况下所采集的线阵图像之间的几何变化差异不大，仅包含平移、尺度和旋转变化，因此也采用面阵图像的几何变换模型对其进行配准。

与面阵图像不同，线阵图像是将线阵相机采集的每一行图像进行拼接而得到的一幅完整二维图像，其获取机制有着本质上的不同。当线阵相机以任意姿态成像时，所采集的线阵图像间的几何变换关系与面阵图像不同（Fang 等，2022b），这导致以面阵图像几何变换模型为基础的直接配准算法不能对任意姿态下线阵相机采集的图像实现几何对齐。为了解决线阵相机相对运动方向平行于目标情况下所采集的线阵图像的配准问题，如前文提到的TEDS，Fang 等人（2022a）建立了相关的几何变换模型，为这种情况下的线阵图像配准提供了几何变换基础。

为了解决现有的直接配准方法无法实现线阵相机以非平行于目标姿态成像时图像配准的问题，本文提出了一种几何联合分段亮度的线阵图像直接配准方法。考虑图像亮度衰减现象，根据线阵相机的特性采用分段亮度模型表达全局亮度变换，联合线阵图像的几何变换模型（Fang 等，2022a），建立了基于图像灰度的误差平方和（sum of squared difference，SSD）配准目标函数。由于几何变换模型和亮度变换模型不同于面阵图像配准时采用的模型，本文基于高斯—牛顿法重新推导了几何参数和亮度参数的求解过程。针对待配准线阵图像可能存在较大的尺度差异，设计了一种初值快速搜索策略。该策略可以提供一个更合理的初始值，使得模板图像和目标图像在几何上更接近。最后在线阵图像上进行的配准对比实验验证了本文提出的几何联合分段亮度线阵图像直接配准方法的精确性和鲁棒性。

1 理论背景与分析

1.1 线阵图像的几何变换模型

当线阵相机无法保证其成像平面与被拍摄目标平行成像时，面阵图像中表征最复杂几何变换的投影变换模型也不能满足线阵图像的几何变换关系。根据Fang 等人（2022a）的工作可知，两幅线阵图像间的几何变换关系为

式中，T和I分别为模板图像和目标图像，图像中的像素点坐标分别用z*=（x，y）T和z=（u，v）T来表示，w为尺度因子，g=［g1，…，g8］是线阵图像几何变换模型中的参数，W表示几何变换。

1.2 分段亮度变换模型

线阵相机具有单线像素数大、成像快的特点，多用于对具有大轮廓且运动的物体成像。为了满足应用需求，通常会搭配大视场角的镜头组成采集系统。根据光度学理论可知，像面照度符合下面的关系（叶玉堂 等，2011），即

式中，E0为沿主光轴方向通过镜头到达像平面的光强度，E为与主光轴成θ角度方向通过镜头到达像平面的目标的光强度。

根据式（2）可知，镜头的视场角越大，视场边缘的像面照度就越低。线阵相机每次成像只能获得高度为1 行的图像，其像面照度呈现出中间强并向传感器两侧衰减，拼接后的图像呈现出垂直于拼接方向中间亮两侧暗的现象，如图1 所示。显然亮度恒常假设（Silveira 和Malis，2007）或全局增益—偏置模型（Li 等，2016）无法表征待配准线阵图像之间的亮度变化关系。因此，根据线阵相机的成像特点，将线阵图像沿着传感器方向分成n段，每段都有独立的增益参数，偏置参数全局相同。分段增益—偏置亮度变换模型为

图1 线阵图像亮度衰减示意图Fig.1 Schematic diagram of the line-scan image brightness attenuation

式中，i表示线阵图像被分段数的索引，ai表示第i段子图像的增益参数，b表示全局偏置参数，p=［ai，b］。I和I*表示变化前后图像中像素的灰度值矩阵；zi表示在第i段子图像中的像素坐标，P表示亮度变换。

2 几何联合分段亮度的线阵图像直接配准算法

本节首先根据线阵图像的几何变换模型和分段亮度变换模型建立线阵图像配准的优化目标函数，并重新推导出求解该目标函数所需的雅可比矩阵（韩冰心 等，2021）和黑塞矩阵（尹奇跃 等，2021），设计了一种初值快速搜索策略，最后给出配准算法的相关流程。

2.1 线阵图像直接配准目标函数

以目标图像和模板图像之间的灰度误差平方和作为图像配准的度量指标。首先根据式（1），将目标图像做几何变换，再根据式（3）对几何变换后的目标图像做亮度变换，最后与模板图像计算二者之间的SSD 值。线阵图像的配准优化目标函数可表示为

式中，i表示亮度变换参数中增益的数量，即图像被分成的段数，blocki表示第i段子图像。

2.2 目标函数的求导

若假定当前的几何变换参数和亮度变换参数已知，即q=［g，p］T已知，可以将迭代求解q转为求解其增量Δq=［Δg，Δp］T，待优化目标函数转化为

式中，J（g）是当几何参数为g时z坐标处的雅可比矩阵。

将式（7）展开，并忽略二次项，得

SD表示下降梯度，具体为

式中，J（p）表示亮度参数为p时z坐标处的雅可比矩阵。∇I=（∇Ix，∇Iy）表示目标图I在x和y方向的梯度；Jw表示几何变换的雅可比矩阵，根据式（1）得

式中，d1=g1x+g2y+g3，d2=g7x+g8y+1，x和y为像素z的横纵坐标。

此时，式（8）已经转化为一个线性最小二乘问题，可以通过正规方程来求解，即

重复以上过程，直到满足迭代次数或Δq小于给定的阈值ε，即

2.3 初始值快速搜索策略

由2.2 节可知，在迭代求解目标函数时假定几何变换参数和亮度变换参数的初始值已知。当两幅待配准图像之间的几何形变较小时，单位变换的值在几何变换最优解的附近，可以作为迭代求解的初始值，即g=［1，0，0，0，1，0，0，0］。线阵相机的传感器像素数大，当相机与运动速度不匹配时，目标在图像上可能出现较大的尺度差异。此时，单位变换作为初始值无法保证其在两幅待配准图像几何变换最优解的附近，导致整个优化过程不收敛。因此，本文提出了一种初始值快速搜索策略，记为FM（initial value fast matching method）。该策略运行速度快，并且得到的初始几何变换参数可以让目标图像在几何变换后包含更多模板图像中的内容，即提供了一个更合理、更接近最优解的初始值。

FM包括如下5个步骤：

1）在模板图像上选择4 块子模板图像，如图2（a）所示；

图2 初始值快速搜索策略示意图Fig.2 Schematic diagram of the initial value fast matching method

2）4 个子模板图像T1-T4分别在目标图像指定区域进行模板匹配，如图2（b）所示；

3）计算每一次搜索的互相关系数，并找到最优的平移量，如图2（c）所示；

4）选取最优匹配位置在水平方向和垂直方向上最小和最大的坐标，以保证目标图像在几何变换后的内容尽量包含模板图像，即

5）根据式（15）所选择的坐标找到其在子模板图像上对应的坐标点，通过这4 对坐标点求解以下几何变换模型中的参数，具体为

式中，sx和sy分别表示目标图像在x和y方向的尺度变换，tx和ty分别表示目标图像在x和y方向的平移量。

将FM 的结果作为线阵图像配准的初始解，即g=［sx，0，tx，0，sy，ty，0，0］。结合初始值快速搜索策略，几何联合分段亮度的线阵图像配准算法（geometric and piecewise photometric registration combined with initial value fast matching method，FMGPPR）流程如下：

输入：模板图像T和目标图像I，子模板尺寸，快速模板分块匹配时的搜索步长，搜索区域尺寸，模板图像分段数i，亮度变换初始值设为p=［1（1×i），0］，最大迭代次数iter，阈值ε。

输出：模板图像T和目标图像I配准时几何变换参数g和亮度变换参数p。

3 实验结果

为了验证本文建立的几何联合分段亮度线阵图像配准算法的性能，实验将从以下3 个方面对算法进行评估：1）初始值快速搜索策略是否可以提高配准算法的配准成功率；2）本文提出的配准方法与采用不同几何变换模型和亮度变换模型的配准方法的比较；3）对实际应用场景中采集的列车图像配准结果的比较。所有的配准实验均基于Intel i7-4790 CPU，3.60 GHz 和RAM 8 GB 的硬件 平台以 及MATLAB R2017b的软件平台实现。

3.1 实验数据和评价指标

为了获得不同位姿下线阵相机采集的图像数据，本文搭建了线阵图像采集系统，如图3 所示。采集系统包括一维运动平台、平面目标、线阵相机和三脚架。为了保证目标的平整性，本文将采集的平面目标粘贴在一个平整的木板上。将平面目标置于平台上匀速地在线阵相机前通过，完成平面目标的一次图像采集。平移和旋转三角架以实现线阵相机的位姿变化，使得平面目标在线阵图像中产生不同的几何变化。多次重复采集过程，形成线阵图像数据集。本文对印有“汉字”的平面目标进行采集，并命名为“汉字”线阵图像数据集。该数据集包含47 幅线阵图像，图4 列出了数据集中的部分线阵图像，其中图4（a）被选为参考图像，方框中的部分为模板图像，如图4（b）所示。图4（c）（d）为数据集中线阵图像的示例，它们将和数据集中的其他图像作为目标图像，分别与模板图像配准。

图3 线阵图像采集系统Fig.3 Line-scan image acquisition system

为了更加直观地反映出线阵图像配准后在几何上的误差，本文对“汉字”数据集中的所有图像手动标注了10 个特征点，如图4 中的星号所示。图像配准后所得到的几何变换矩阵，可以将目标图像中的标注点坐标映射到模板图像坐标系上。如果配准后的两幅图像在几何上一致，那么所有的标注点都应该重合。所以，计算模板图像和目标图像上对应标注点的坐标误差，并将其作为两幅线阵图像配准后在几何上误差的衡量指标。标注点坐标的几何误差Eg计算为

式中，φI和φT表示目标图像和模板图像中标注点的坐标；n表示标注点的序号，N表示标注点的数量。

对于配准后两幅图像在亮度上的误差，将以它们的灰度均方根误差Ep作为衡量指标，计算为

式中，n表示模板图像的像素序列，N表示模板图像像素数量。

3.2 初始值快速搜索策略评估

本节将分别采用单位变换以及模板匹配和初始值快速搜索策略获得的几何变换参数作为迭代求解的初始值去配准两幅线阵图像，配准算法分别记为I-GPPR（geometric and piecewise photometric registration combined with identity warp）、TM-GPPR（geometric and piecewise photometric registration combined with template match）和FM-GPPR。对于采用单位变换为初始值的配准，配准算法不执行FM-GPPR 中的步骤1，几何变换的初始值为g=［1，0，0，0，1，0，0，0］；对于采用模板匹配方法获得初值时，配准算法同样不执行FM-GPPR 中的步骤0，而是将整幅模板图像以5 个像素为步长在目标图像上滑动，并计算每一步的互相关系数，通过最大互相关系数确定其最优平移量tx和ty，那么配准时的几何变换初始值为g=［1，0，tx，0，1，ty，0，0］。当采用FM 策略获得初始值时，子模板区域大小为200 × 200 像素，搜索区域为目标图像尺寸的1/5，搜索步长为5 个像素。3 种初始值配准时均采用分段亮度模型。由式（2）可知，相同分辨率图像的亮度衰减程度也可能不同。针对本文采集的“汉字”线阵图像数据，以下的配准实验中均将模板图像分为10 段，即亮度变换参数初始值为p=［11×10，0］。在确定亮度变换初始值和3 种几何变换初始值后，后续的迭代求解过程完全相同，即执行FM-GPPR 中的步骤1）—9）的循环过程。采用3种初始值配准时的最大迭代次数为200，阈值为10-8。通过几何误差Eg（初始值情况和配准后的情况）、运行时间、迭代次数和配准成功率去衡量本文设计的初始值快速搜索策略对配准算法性能的影响。

图5 为“汉字”线阵图像数据集在采用3 种初始值配准时的结果。图5（a）列出了模板图像和目标图像在3种初始值时的几何误差。显然，基于FM 策略提供的初值可以使模板图像和目标图像在几何上更接近。图5（b）给出了配准后的几何误差。可见，采用FM 策略提供初值配准后的几何误差更小。如果几何误差Eg小于1 个像素，则认为迭代过程是收敛的，两幅图像的配准是成功的，表1 给出了采用3 种初值配准后的成功率。FM-GPPR 的配准成功率达到100%，TM-GPPR 的配准成功率仅有43.5%，而I-GPPR 的配准成功率则为0%。图5（c）给出了采用3 种初始值配准的运行时间（初值计算时间和迭代求解时间的总和），可见以FM 获得的初值配准算法运行的总时间更少。表1 列出了数据集中所有图像的初值计算时间的平均值，虽然FM 需要额外的1.68 s 计算时间，但由于其提供了一个更接近最优解的初始值，使得采用该值配准时算法的迭代次数更少，如图5（d）所示。

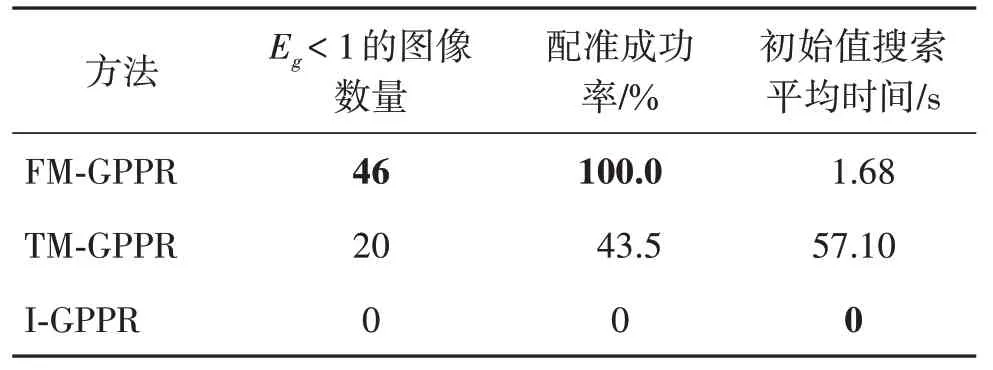
表1 3种初始值的平均搜索时间及采用它们配准的成功率Table 1 The average search time of three initial values and the success rate of their registration

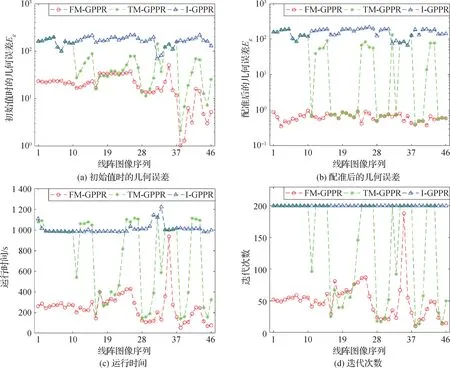
图5 “汉字”线阵图像数据集在采用3种初始值配准时的结果Fig.5 The registration results of Chinese characters line-scan image dataset with three initial values

综上，对比实验的相关结果证实了本文设计的初始值快速搜索策略可以提高线阵图像配准算法的性能。这源于该方法使用更小的搜索模板在目标图像上固定区域滑动搜索，减小了参与计算的总像素数，减少了滑动搜索的次数，降低了初值的计算时间；同时，该步骤获得的初值可以减小待配准图像在几何上的差异，使得模板图像和目标图像在几何上更接近，不仅减少了算法的迭代次数，更提高了配准的成功率。

3.3 配准方法评估

本文建立的优化目标函数中采用了线阵图像几何变换模型和分段增益—偏置亮度模型。所采用的几何变换模型不同于面阵图像的几何变换模型，同时分段亮度模型也有更多的参数需要求解。所以，为了验证本文算法的配准性能，将进行如下对比实验：分别考虑几何配准GR（geometric registration）、几何联合亮度配准GPR（geometric and photometric registration）和本文提出的几何联合分段亮度配准FMGPPR 去对齐线阵图像；同时也将以Chen 等人（2018）提出的归一化总梯度配准NTG（normalized total gradient）、Li 等人（2018）提出的几何联合亮度李群配准GPL（geometric and photometic Lie algebra）和Cao 等人（2020）提出的结构一致性配准SCB（structural consistency boosting）这3 种直接图像配准算法作为横向对比实验。为公平起见，所有配准实验的初始值都由初始值快速搜索策略提供，子模板区域为200 × 200 像素，搜索区域为目标图像尺寸的1/5，搜索步长为5 个像素。最大迭代次数为200，阈值为10-8。6 种配准算法分别记为：FM-GR、FMGPR、FM-GPPR、FM-NTG、FM-GPL 和FM-SCB。其中，NTG 和SCB 金字塔的层数为4 层。它们采用的几何变换模型、亮度变换模型及初始值如表2 所示。本文将通过配准后的几何误差Eg、运行时间、迭代次数、亮度误差Ep和成功率来验证配准算法的性能。

表2 6种配准方法的相关信息Table 2 Information about the six registration methods

图6 列出了“汉字”线阵图像数据集的配准结果。图6（a）给出了数据集中的线阵图像在配准后的几何误差情况。可见，基于本文提出的方法配准后的模板图像与目标图像间的几何误差最小。图6（b）（c）分别给出了对比实验的运行时间和迭代次数。由于GPL、NTG 和SCB 都不需要反复计算黑塞矩阵，这些算法的迭代速度更快，即使在较多迭代次数的情况下其运行时间也相对较少，但是配准后图像间较大的几何误差不能突出它们在运行速度上的优势。分段亮度模型需要求解更多的参数，但由于该模型更符合线阵图像的亮度变化，使得算法每次迭代的收敛效率更高，相比于FM-GPR 和FM-GP，其迭代次数更少，可在更短的运行时间内收敛。图6（d）给出了配准后图像亮度的误差情况。从图中可以清晰地看出，基于分段亮度模型配准后的图像亮度误差更小，优于未考虑亮度变换和仅考虑全局亮度变换模型的配准方法。

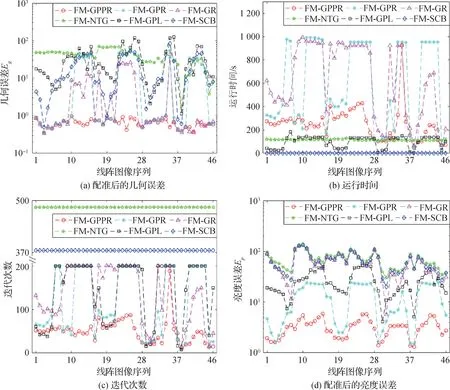
图6 6种方法在“汉字”线阵图像数据集的配准结果Fig.6 The registration results of six methods on Chinese characters line-scan image dataset

如果几何误差小于1 个像素，则认为迭代过程是收敛的，6种方法在“汉字”线阵图像数据集（46幅）的配准成功率如表3 所示。从表3 可以看出，FMGPPR 的配准成功率达到100%，FM-GPR 和FM-GR的配准成功率仅有60.9%和67.4%，说明采用分段亮度变换模型对线阵图像亮度衰减具有更高的鲁棒性；SCB 的配准成功率仅为8.7%，而NTG 和GPL 的配准成功率均为0，意味着面阵图像的几何变换模型不符合线阵图像的几何变换规律，也说明了只有本文提出的线阵图像配准算法可以实现非平行姿态线阵相机采集的图像的配准问题。

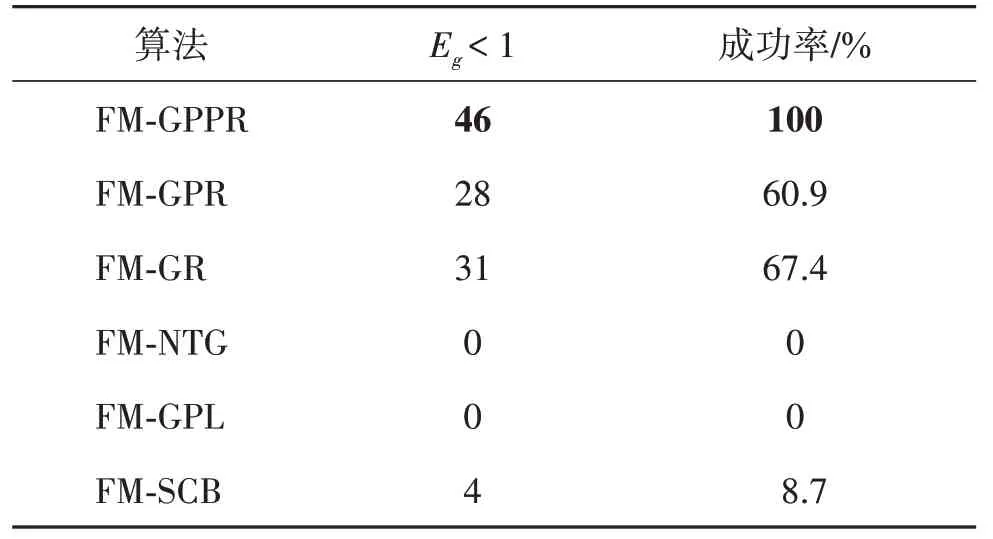
表3 6种方法的配准成功率Table 3 Registration success rate of six methods

为了更直观地观察模板图像和目标图像配准后在几何上的差异，图7 列举了“汉字”线阵图像数据集中某个目标图像配准后的结果。由于考虑分段亮度模型配准后的目标图像与模板图像在亮度上的误差很小，这将导致目标在它们的差值图像中很难分辨，所以图7 列出的结果是将配准后的目标图像与模板图像进行Alpha-blend 混合叠加生成，而配准前后的几何误差Eg和亮度误差Ep在相应的叠加图像下方给出。图7（a）给出了模板图像和目标图像未配准时的叠加图像，可以看出图中的汉字并没有对齐；根据Eg和Ep的值可知它们在几何和亮度上都存在较大的差异。图7（b）给出了基于本文方法配准后的叠加图像，示例中的汉字完全对齐，几何误差小于1个像素，同时亮度误差也非常小。图7（c）（d）分别给出了基于FM-GPR 和FM-GR 方法配准后的叠加图像，未对齐的汉字表明它们并没有几何对齐。因为FM-GR 方法中没有考虑亮度变化，假设亮度恒常去配准存在亮度变化的图像显然是不稳健的；而FM-GPR 方法虽然考虑了亮度变化模型，但是其未考虑大视场镜头采集的图像存在亮度衰减现象，使得全局亮度变换模型对亮度衰减不鲁棒，不能胜任线阵图像的配准问题，导致其无法在几何上对齐。NTG、SCB 和GPL 配准方法分别使用了面阵图像的仿射变换模型和投影变换模型，由于这些模型都不符合线阵图像的几何变换规律，其配准后的图像也无法在几何上对齐，如图7（e）—（g）所示。

图7 6种方法配准后的叠加图像Fig.7 Overlapped images after registration of six methods

3.4 列车线阵图像配准结果

本节将对列车线阵图像进行配准实验，验证本文提出的线阵图像直接配准方法对实际应用场景所采集的线阵图像的配准性能。实验图像由安装在铁轨两侧的线阵相机采集。根据实际需求，线阵相机安装在铁轨沿线不同的位置，但是相机相对于铁轨的姿态无法保证相同，导致所采集的列车图像存在一定的几何差异。

图8 列出了本节配准实验所使用的列车线阵图像数据，从左到右依次命名为注砂口、车钩机构和侧板。每种数据包含6 幅图像，其中，图8 的第1 行选为模板图像；图8 第2 行为3 种数据中的图像示例，它们和数据集中剩余的图像选为目标图像，分别与其所对应的模板图像进行配准。为了计算两幅线阵图像配准后的几何误差，对列车图像分别进行了手动标注，如图8中的星号所示。在本小节的配准实验中，将采用本文提出的FM-GPPR 配准方法对列车图像进行配准，其中模板图像分为10 段，即亮度变换参数的初始值为p=［11×10，0］，阈值ε设定为10-8，最大迭代次数为400 次；快速模板匹配算法中子模板图像大小为模板图像大小的2/3，搜索区域为目标图像大小的1/5，搜索步长为5 个像素。作为对比实验，列车图像也将由NTG（Chen 等，2018）、GPL（Li等，2018）和SCB（Cao 等，2020）3 种直接配准算法进行配准，其初值由初始值快速搜索策略提供，亮度初值参数为p=［1，0］。

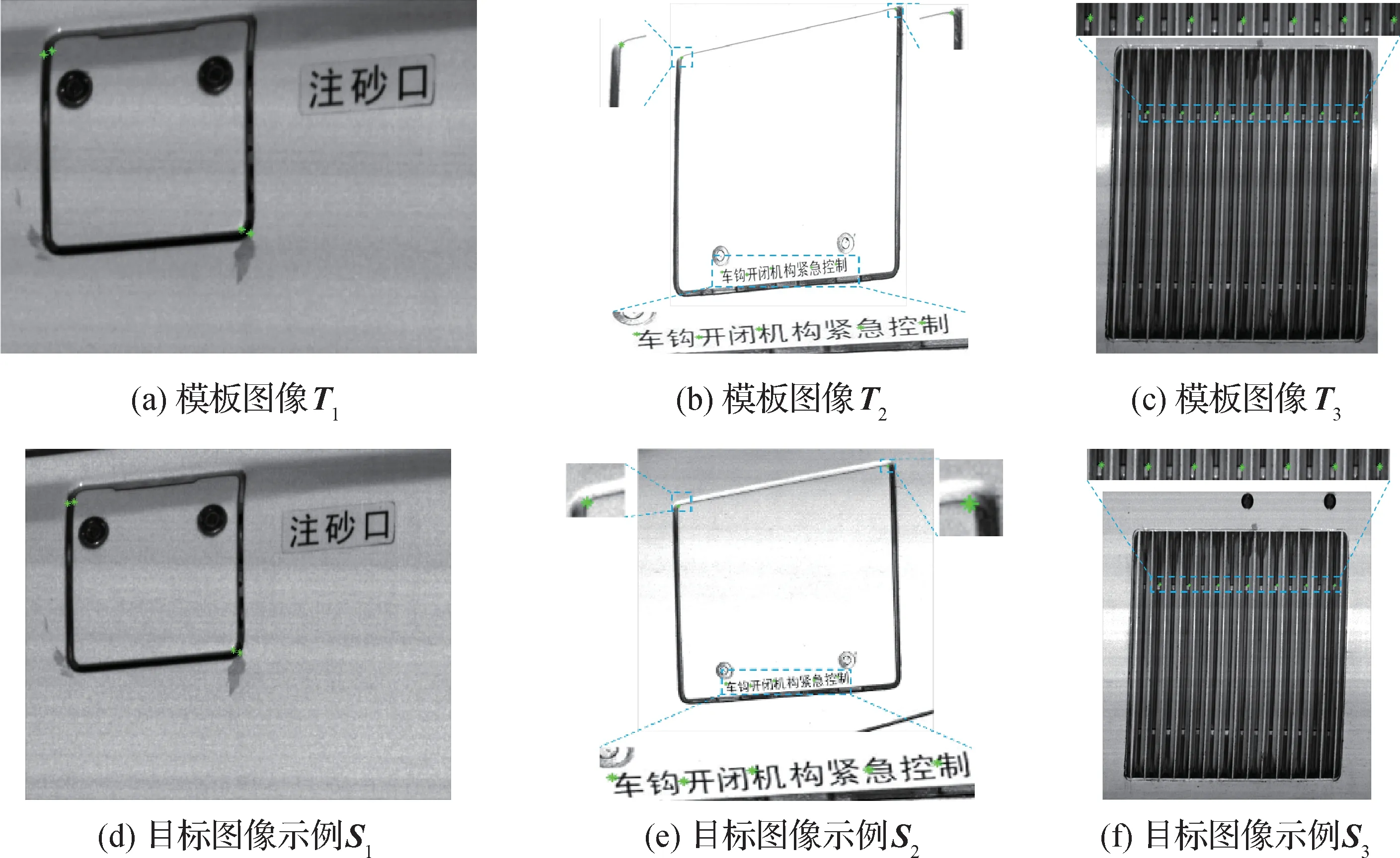
图8 列车线阵图像数据示例Fig.8 Line-scan images of EMU（electric multiple units）train（（a）template image T1；（b）template image T2；（c）template image T3；（d）target image S1；（e）target image S2；（f）target image S3）

图9 给出了图8 中第2 行示例列车图像的配准结果，这些结果以伪彩图的形式呈现。几何误差Eg和亮度误差Ep标注在相对应的伪彩图下方。根据未配准时的伪彩图可知它们在几何上存在较大的差异。通过对比配准结果可知，基于FM-GPPR 方法配准后的几何误差Eg均小于1 个像素，亮度误差Ep也优于其他3 种配准方法，说明本文提出的线阵图像配准方法具有更高的几何对齐精确性和更强的亮度变换鲁棒性。

图9 列车图像的配准结果Fig.9 Registration results of EMU train（（a）without registration；（b）FM-GPPR；（c）FM-NTG；（d）FM-GPL；（e）FM-SCB）

表4 列出了3 种列车数据集中所有图像在配准后标注点的几何误差情况。可见，基于本文方法配准后的两幅列车图像几何误差最小，均优于其他3种方法。

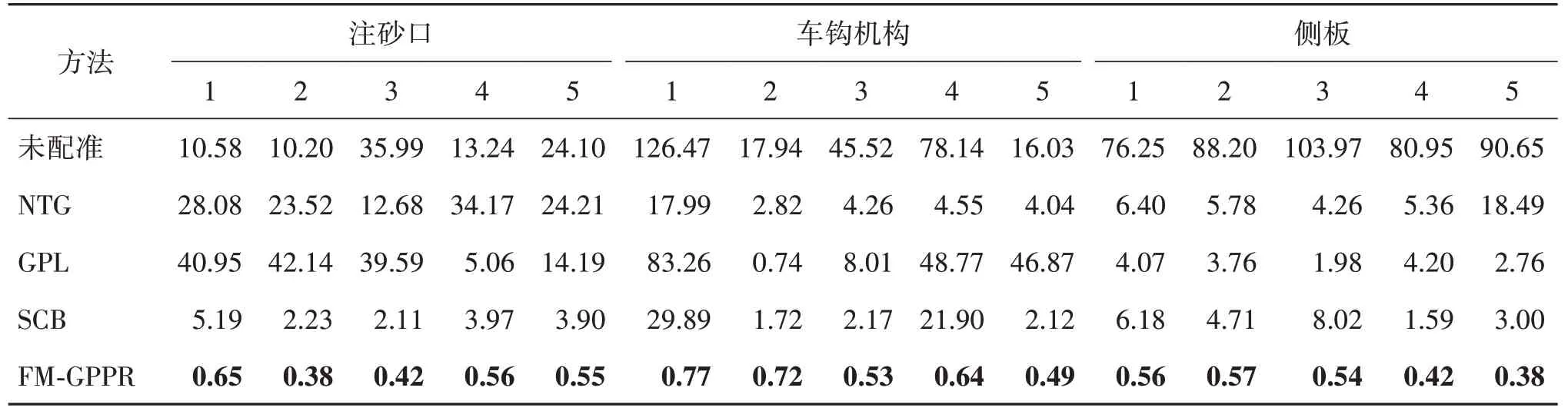
表4 列车图像配准后标注点的几何误差EgTable 4 Eg of annotation points in the train image after registration

4 结论

本文提出了一种考虑几何变换和亮度变换的线阵图像直接配准方法，建立了基于线阵图像几何变换模型和分段增益偏置亮度模型的图像配准目标函数，解决了非平行姿态下线阵相机所采集图像的配准问题。该方法首先通过初始值快速搜索策略得到一个初始解；再根据高斯—牛顿法迭代求解出目标函数中的几何参数和亮度参数。在本文采集的线阵图像数据集和真实应用场景采集的列车线阵图像上进行了相关的配准对比实验。结果表明，本文提出的线阵图像直接配准方法对线阵图像亮度变化及亮度衰减具有很强的鲁棒性，可以更有效地配准两幅线阵图像，使它们在几何上更精确地对齐。本文方法不再局限于线阵相机成像平面平行于目标时采集图像的配准问题，拓宽了线阵相机的使用范围。

由于线阵图像和面阵图像的几何变换规律不同，因此本文方法局限于线阵图像的配准问题。在迭代求解过程中需要反复计算雅可比矩阵和黑塞矩阵，使得配准时间过长。因此，下一步工作将围绕以下两个方面展开：1）提升算法的计算效率；2）实现基于线阵图像配准的列车异常检测。