利用可变预测的密文域可逆信息隐藏

陈佳妮，徐达文

1.安徽理工大学数学与大数据学院，淮南 232001；2.宁波工程学院网络空间安全学院，宁波 315211

0 引言

随着云计算和云存储发展，人们越来越倾向于使用云服务器保存自己的多媒体内容，如图像、视频等。这一操作为用户提供便利的同时，也带来了一些信息泄露的问题（Chang 等，2018）。研究者以保护用户隐私和完整传输数据为研究目的，派生出加密域图像可逆信息隐藏（reversible data hiding in encrypted image，RDHEI）。这项技术不仅关心秘密信息的嵌入和提取，还要求图像载体在无论是否提取信息的情况下可完全复原，从而应用于军事、医学等一些对图像质量高敏感的特殊场合。

RDHEI 方法中存在3 个相互独立的角色，即图像持有方、服务运营方和图像接收方。持有方将加密图像上传云端，运营方会在云服务器中出于管理等目的对上传的图像嵌入一些必要信息，接收方获得嵌入信息后的加密图像，根据所拥有的密钥进行提取信息或恢复图像操作。现有RDHEI 方案可分为两类：加密后腾出空间（vacating room after encryption，VRAE）和加密 前预留空间（reserving room before encryption，RRBE）。如图1 所示，这两类方法的最大区别在于加密阶段前后流程的不同。对于RRBE 来说，图像持有方在将图像上传给服务运营方前，需要进行一些必要的预处理以保留数据空间。对于VRAE 来说，则是图像持有方直接上传加密图像，由运营方做出腾出数据空间的操作，为后续的嵌入做准备。实际上，两类方法的腾出空间操作都是对图像的一个冗余处理，核心在于选择利用像素相关性的时机。

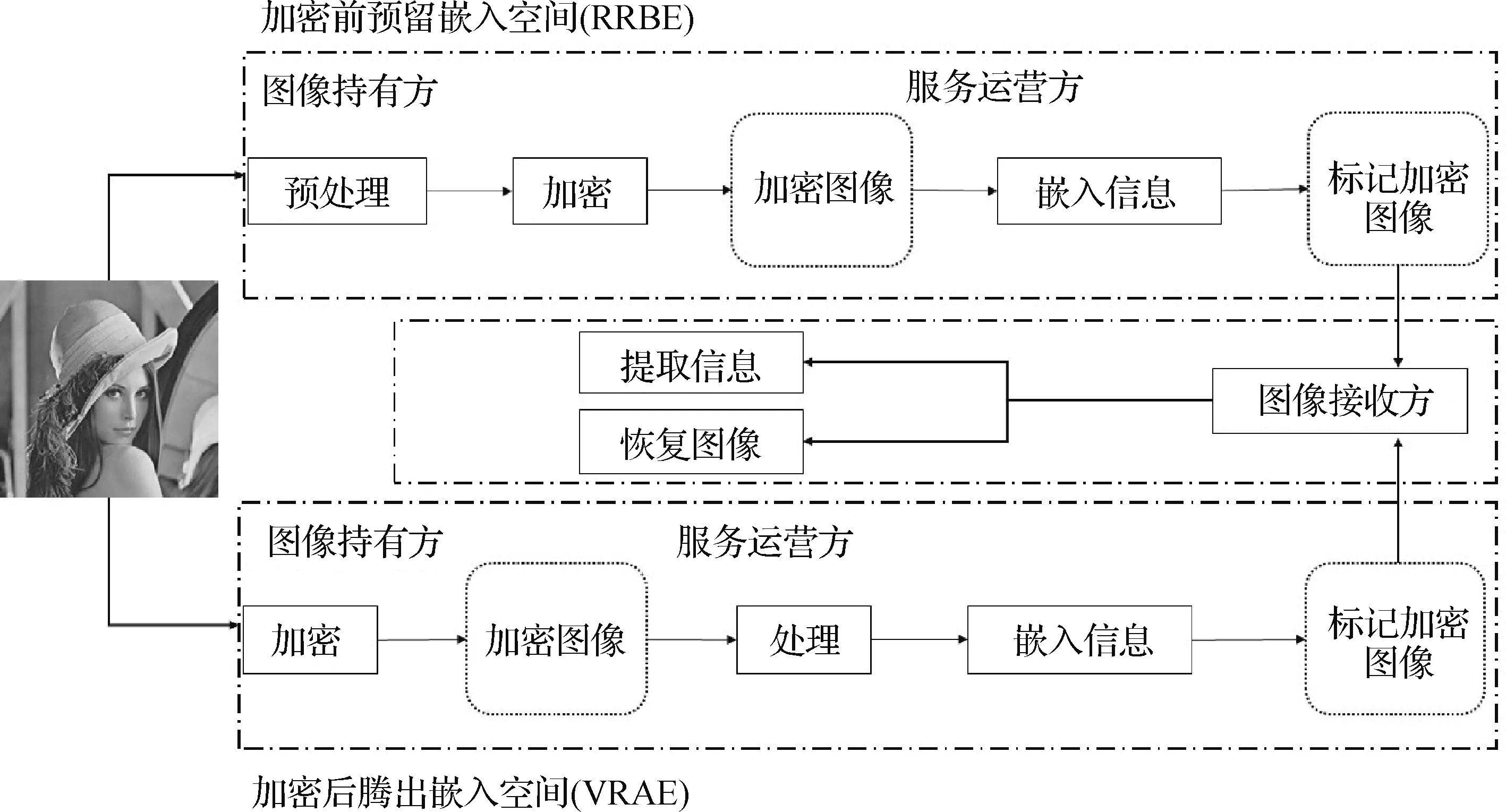
图1 RRBE和VRAE的流程图Fig.1 Flow chart of RRBE and VRAE

VRAE 直接对图像加密后上传到云端，避免预处理过程的泄露与附加信息导致的图像破译，同时也减轻了图像持有方的计算负担。Zhang（2011）提出一种VRAE 算法，将图像加密后分块，每个块分为两个子集，根据嵌入信息的比特值选择翻转其中一个子集的3 个LSB（least significant bit）。Hong 等人（2012）改进了Zhang（2011）的算法，实现更好地预估像素。Zhang（2012）还提出一种可分离的可逆信息隐藏算法，支持图像恢复与信息提取。为了降低误码率，Wu 和Sun（2014）提出基于预测误差的方案，保证嵌入数据无误提取。Ge 等人（2019）和Wang 等人（2022）都采用块置换与像素异或的加密方法，能有效抵抗唯密文攻击。但都只能利用局部相关性以获得嵌入空间，前者选取块内峰值像素，修改其他像素值完成信息嵌入；后者借助块内产生的预测误差直方图，通过峰值平移实现数据的多级嵌入。Liu 和Pun（2022）通过设置3 个参数将像素的8 个位平面分为高阶位平面、中阶位平面和低阶位平面，将块内像素中相同的高阶位平面替换为低阶位平面，从而生成有效嵌入空间。Wu 等人（2021a）提出块内差分编码算法，即把图像分块后，根据中心像素与周围像素的最大差值分为8 种标记块，使秘密信息依据标记符嵌入。Wang 和He（2022）以及Gao 等人（2022）则分别提出不同的标签编码策略来标记块内像素冗余，得到一个较高的嵌入容量。Yi和Zhou（2019）提出参数二叉树标记（parametric binary tree labeling，PBTL），用不同的编码长度标记可嵌入的像素。随后，Wu等人（2020）提出改进的参数二叉树标记算法。Xu 等人（2018）以及Xu 和Su（2021）提出不同的直方图移位策略，后者比前者减少了图像质量的损失。Qin 等人（2019）提出位平面无序和稀疏矩阵编码的方法，将MSB（most significant bit）的冗余转移到LSB，进一步提高加密图像的安全级别。

相对于VRAE，RRBE 则可以利用明文图像的空间相关性。Xu 和Wang（2016）提出一种可分离、无差错的RRBE 算法。Ma 等人（2013）提出在加密前腾出空间，通过替换LSB来插入数据，虽然有效载荷有所提升，但是LSB的预测准确率较低，导致图像质量在一定程度上的损失。由于在图像预测中最高位平面的预测准确度远远高于最低位平面，Puteaux 和Puech（2018）首次提出基于MSB 预测的密文图像可逆信息隐藏算法，然而这个算法只使用一个最高位平面。Yi 等人（2018）在此基础上提出了两个MSB平面替换的算法，有效提升嵌入率。Yu 等人（2022）提出在3 × 3 块中翻转一个像素的MSB 来嵌入信息的方案，并采用P-M 噪声消除模型来恢复模型。Manikandan 和Zhang（2022）为了达到更高的恢复率，将图像分割为更小的像素子序列，翻转其中偶数位置的像素MSB 实现信息嵌入。Fu 等人（2019）提出使用反向哈夫曼编码标记不同的MSB 类别，压缩在可嵌入的MSB层中。Chen和Cheng（2019）提出联合使用游程编码与块重排的方法，Yin 等人（2022）则使用位平面重排，比Chen 和Cheng（2019）实现更有效的压缩。

为了进一步提升冗余利用率，Yi 和Zhou（2017）提出了二进制块嵌入（binary-block embedding，BBE）方法，把每个位平面按大小分为好块和坏块，对其采用块长度可变的自适应标签。Chen 等人（2021）从减小加密图像的文件大小的角度出发，提出一种基于多个高位平面预测和压缩编码的加密图像算法。Zhang 和Luo（2022）通过矢量滑动直接比较相邻像素的前b位MSB的冗余程度，得到参数b和冗余像素数量的最佳折衷位置图，提出了两种多MSB 替换方法。Yin 等人（2021）在对预测后的像素块作统一块与非统一块的区分之后，进一步将非统一块按T 子型划分，把符合嵌入规则的非统一块的中心也用做嵌入信息。Wu等人（2021b）提出基于预测误差标记的算法，自适应标记低频预测误差与高频预测误差。杨尧林等人（2023）在此基础上进一步发现未利用的冗余，提出MSB 二维标记的方法。Yin 等人（2020）将哈夫曼编码应用于多MSB 的自适应编码，实现高嵌入容量。Mohammadi等人（2022）提出基于局部差分预测和块容量标签的算法。Chen 和Chang（2022）通过块间的像素预测与MSB比较，得到自适应编码。

为了在冗余处理和嵌入容量之间建立平衡点，本文提出了一种基于可变预测和多MSB 替换的密文域可逆信息隐藏算法，通过可变预测位平面翻转实现冗余处理，用多MSB 替换获得较好的嵌入能力。本文工作的主要贡献如下：1）充分利用像素之间的相关性，通过可变预测位平面翻转的操作，使位平面预留出更多可嵌入空间，提高了嵌入容量。可变预测位平面翻转的逆操作也支持原始图像的无损恢复。2）通过算术编码压缩了具有稀疏特征的位置图，并将整个密文域可逆信息隐藏过程所需的辅助数据全部嵌入加密图像中，在传输过程中不需要处理其他额外开销或文件。3）通过基准BOWS-2 数据集测试证明，实现了较高的有效载荷，平均嵌入率为2.953 bit/像素。

1 可变预测位平面翻转

现有RDHEI 算法中，像素预测方法主要包括中值边缘检测器（median edge detector，MED）、梯度调整预测因子（gradient adjusted predictor，GAP）、菱形预测器和线性预测器。Wang等人（2022）、杨尧林等人（2023）以及Yin等人（2020）利用MED预测得到原始像素的预测误差。然而，预测误差不可避免会产生关于差值的正负号问题，研究者为了完全恢复图像，需要用一个二进制位置图来存储此信息。Wu等人（2021a）采用直方图移位法对差分图像进行预处理，以消除正负号带来的额外空间的占用。本文提出可变预测位平面翻转（variable prediction bit-plane inversion，VPBI）策略，目的在于充分利用图像整体的相关性，过程如下。

1.1 预测序列构造

将每一次迭代的像素表示为P={Pk|k=1，2，…，α}，其中α为选定的迭代次数，α∈[2，8]。假设Pk为目标像素，则其相邻像素值Ak，Bk，Ck为参与预测的参考像素，如图2所示。

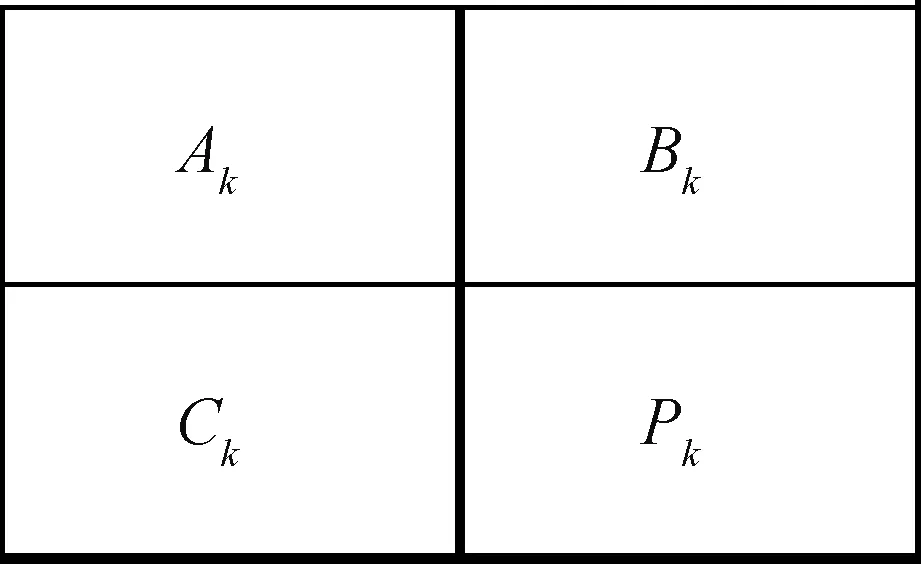
图2 参考像素位置图Fig.2 Reference pixel location

预测序列T={Tk|k=1，2，···，α}，Tk表示存储3个参考像素的可变预测值的序列，具体为

参与预测的3 个参考像素在第1 次迭代中取当前值作为预测值，在第2次迭代至第α次迭代中3个预测值根据判断条件变化，判断条件为前一次迭代的3 个预测值是否大于29-k，其中k为当前迭代数。若3 个预测值均大于29-k，那么当前迭代的3 个预测值分别等于前一次迭代的3 个预测值减去29-k。否则，当前迭代的3 个预测值分别等于前一次迭代的3 个预测值。3 个参考像素的可变预测值计算为

1.2 位平面翻转

将目标像素Pk转化为二进制序列I，具体为

式中，I1为最高位平面，I8为最低位平面，则预测的第k个位平面（即第k次迭代）可以表示为

参数τk计算为

接下来，以一个3 × 3 像素块为例，解释可变预测位平面翻转过程。首先选定P(2，2)为当前迭代像素，则该像素周围的3 个像素P()1，2，P(2，1)，P(1，1)列入预测序列中，假定迭代次数为5，从式（2）—式（4）计算后的预测序列表如表1 所示。在预测序列的第3 次迭代中，由于A2，B2，C2中存在小于29-3即64 的预测值出现，因此第3 次迭代的预测值保持第2 次迭代的预测值不变。

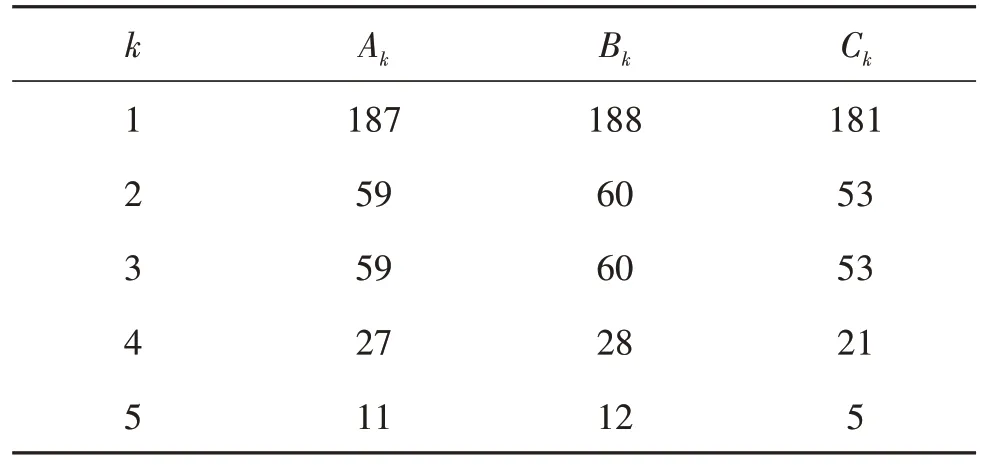
表1 预测序列的例子Table 1 Example of prediction sequence

图3（a）为可变预测位平面翻转的操作过程，图3（b）为前5个位平面翻转对应的计算过程。

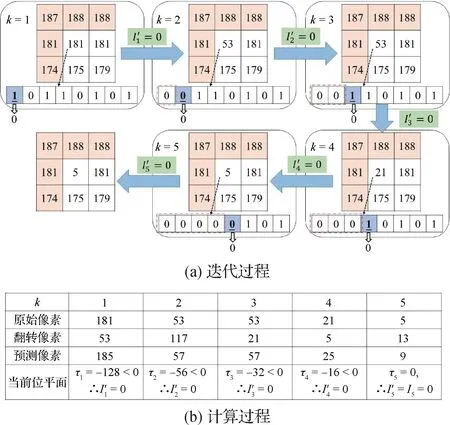
图3 可变预测位平面翻转的例子Fig.3 Example of VPBI

假设图3（a）中的像素P(2，2)=181，对应的二进制序列为10110101。在第1次迭代中，由式（8）计算得到原始像素值P1=181，由式（9）计算得到对应的翻转值Inv1=53，由式（10）计算得到预测值Pred1=0.2 × 187+0.4 × 188+0.4 × 181=185。最后通过式（6）和式（7），计算得到τ1=|181 -185|-|53 -185|=-128。由于τ1＜0，因此将当前位平面比特值修改为0，即I′1=0。在第2次迭代中，由式（8）计算得到像素值P2=53，翻转值Inv2=117，Pred2=57。计算得 出τ2＜0，因 此=0。同样的过程可以应用于其他目标像素，以此得到预测图像。

随着k值的不断增加，|Pk-Predk|的值将会逐渐与|Invk-Predk|接近，这是由于低位平面的相关性没有高位平面紧密。因此，可以推断出高位平面的0的数量会多于1的数量，这是本文提出这个预处理方法的依据。

2 本文算法

本文所提出的RDHEI算法框架如图4所示。在加密阶段，原始图像通过可变预测位平面翻转得到位置图与符号指示图等辅助信息；在嵌入阶段，云端根据MSB 中提取的位置图，确定有效载荷的像素数量，并进行多MSB 替换操作；在解密阶段，解密者可以通过自己拥有的密钥进行信息提取或图像恢复操作。

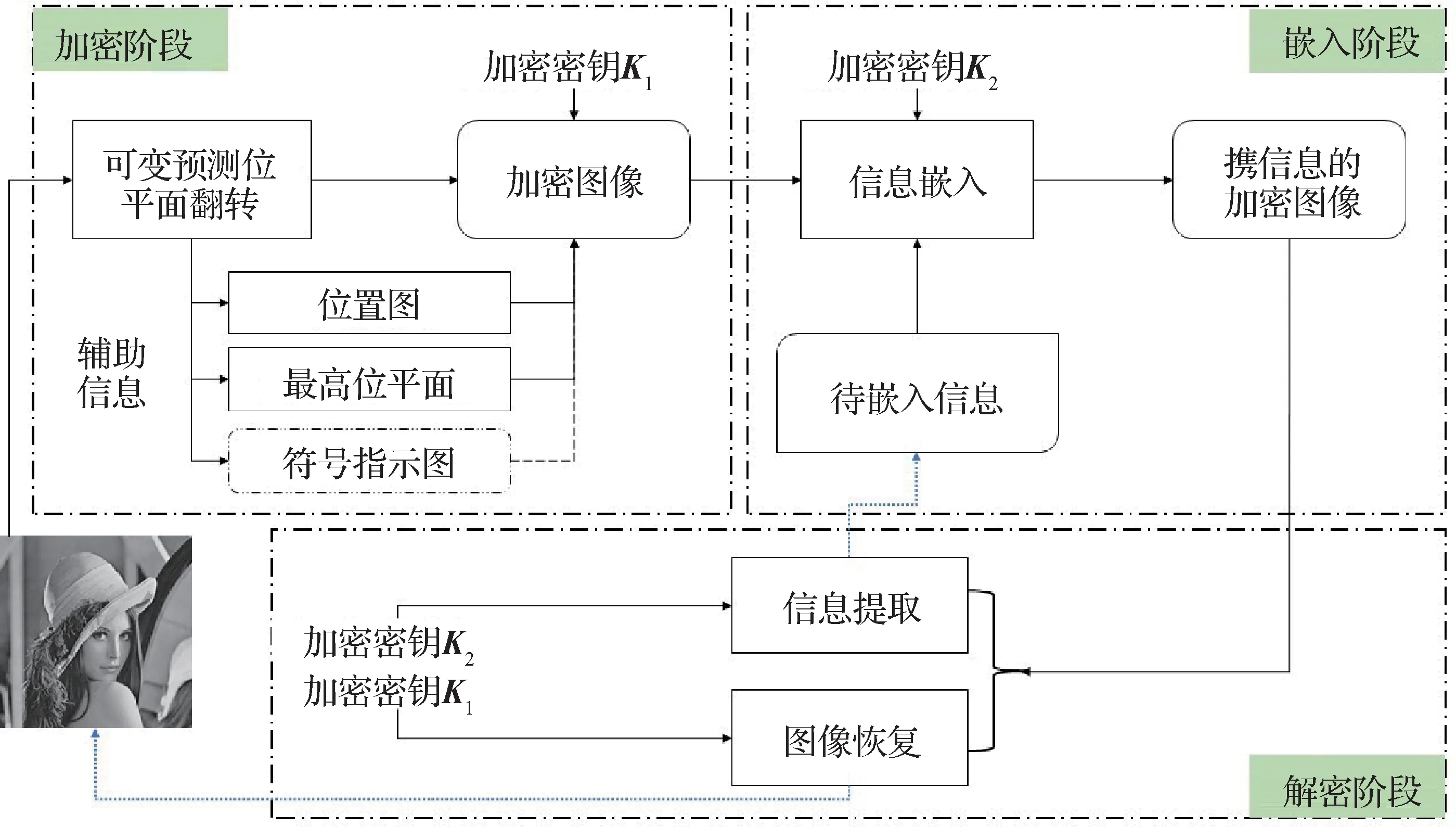
图4 本文算法的框架Fig.4 The framework of the proposed algorithm

2.1 预处理

为了预留空间，图像持有方需要对原始图像进行预处理。预处理分别由可变预测位平面翻转、线性预测与符号指示图生成、位置图生成、最高位平面提取4个阶段组成。

2.1.1 可变预测位平面翻转

设一个尺寸为M×N的原始图像P，P(i，j) (1 ≤i≤M，1 ≤j≤N)为原始图像第i行第j列的像素。保留图像的第1 行和第1 列像素，从第2 行第2 列开始进行可变预测位平面翻转的预测操作，预测像素Ph(i，j)计算为

式中，Pk(i，j)为经过k次迭代后的预测像素值。

2.1.2 线性预测与符号指示图生成

经过可变预测位平面翻转处理后的图像为Ph，为了尽可能增加可嵌入的像素，本文引入了线性预测方法。以Ph(1，1)作为参考像素，得到首行首列的其他像素的预测误差e(i，j)，具体为

由于预测误差存在正负号问题，因此本文拟用1 bit编码存储预测误差符号。

首先，将预测误差的绝对值转换为二进制序列，具体为

随着中药挥发油日益受到人们的重视，其在医药、食品、日化用品、农业等领域都已得到广泛应用。然而，由于中药自身具有成分复杂、有效成分多、含量差异大等特点，加之中药挥发油前处理过程、提取工艺、提取设备等无统一标准，均使得中药挥发油的质量难以控制。同种药材不同产地、同种药材不同厂家、同种药材不同批次均存在质量差异。中药挥发油质量不稳定的问题直接关系到其临床疗效与消费者的安全性、适应性。

然后，将符号存储在最后一个比特位，用0 表示正号，1 表示负号，最后转换为十进制得到像素值，具体为

式中，Ph(i，j)表示坐标为(i，j)的预测值。

根据式（14）可知，在8 个位平面中，预测误差的二进制位至多为7位，即预测误差不可大于127或小于-127。

若预测误差绝对值超过约束范围，则对该值进行预测还原。具体为

式中，Pt(i，j)为图像Pt中坐标为(i，j)的像素，P(i，j)为原始图像P中坐标为(i，j)的像素。

反之，使用上述的预测误差操作得到图像Pt。

由此，需要采用一个符号指示图S定位是否存在无法用8位二进制表示的预测误差，0代表预测误差绝对值不大于127，1 代表预测误差绝对值大于127，即不能存储自身符号位。则符号指示图S的大小为

2.1.3 位置图生成

所提算法中一个重要的部分就是为图像Pt生成位置图L，这是实现多MSB 替换的关键信息。该位置图会针对具体图像进行最优化分析，在嵌入数量和嵌入深度之间选择最佳的参数，判断除首个像素以外的全部像素的多MSB变化。

位置图生成算法过程如下。首先，将图像划分为8 个位平面，以从左到右、从上到下的次序查看前β个高位平面是否全为0，如果是，则在位置图相应的位置标记为0；反之，则标记为1。嵌入深度β∈[2，8]是依据图像自身冗余程度变化的参数。关于迭代次数α与嵌入深度β的选择将在3.5 节详细讨论。因此，位置图生成式为

式 中，L(i，j)为位置图第i行 第j列的标记值，表示图像中坐标为(i，j)的像素第1 至β的位平面。ρ={0，0，…，0}，是一个全0序列。

2.1.4 最高位平面提取

为了算法的完全可逆与辅助信息的嵌入，保存最高位平面H，具体为

为了更加清晰地阐述符号指示图S、位置图L和最高位平面H的生成，以3 × 3像素块为例构造生成过程。假定迭代次数α=5，嵌入深度β=5，则辅助信息的产生过程如图5所示。

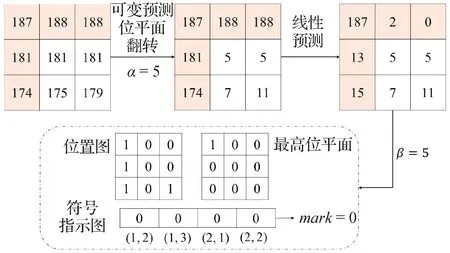
图5 举例像素块的预处理过程Fig.5 Preprocessing process of sample pixel block

像素块通过可变预测位平面翻转、线性预测预处理后，首行与首列的预测误差不存在超出约束范围的值，因此得到全为0 的符号指示图。使mark=0，表示后续无需嵌入符号指示图。β=5 表明选取前5 位高位平面为嵌入位置。若像素点的前5 位高位平面全为0则在位置图相应位置标记为0，否则标记为1。最后提取像素块的最高位平面。

2.2 图像加密

为了防止图像内容泄露，图像持有方预留空间后需要对图像Pt做加密处理。

2.2.1 异或加密

同上，Pt是大小为M×N的8 位灰度图像，图像中第i行第j列的像素为Pt(i，j)，i=1，2，…，M，j=1，2，…，N。在本文算法中，为了减轻服务运营方的负担，保证图像的安全，利用图像加密密钥Ke生成一个与图像尺寸相同的伪随机矩阵V，其值的取值范围为0～255，通过逐位异或（exclusive OR，XOR）得到加密图像Pe，计算过程为

式中，Pe(i，j)是加密图像Pe坐标为(i，j)的像素，V(i，j)是伪随机矩阵V坐标为(i，j)的数值。

2.2.2 辅助信息替换

在图像加密后，进入辅助信息替换阶段。将位置图L、最高位平面H与符号指示图S进行无损压缩，分别表示为Lc，Hc，Sc，按照图6 的顺序依次替换最高位平面。

图6 加密图像的两种最高位平面Fig.6 Two kinds of MSB in encrypted image

考虑到算术编码的压缩效率，位置图的长度记做ℓL，用log2(M×N× 8)比特记录；最高位平面的长度记做ℓH，用log2(M×N)比特记录；在上述符号指示图中已用ℓS表示，用8比特记录长度；标记符mark用1比特存储。加密图像的最高位平面可以表示为

式中，‖ 代表连接符。

2.3 信息嵌入

图像持有方将图像上传到云端服务器后，服务运营方将进入信息嵌入阶段。假设秘密信息为W={w1，w2，…，wn}，为了增强秘密信息的安全性，需要用信息加密密钥Kd随机生成的二值序列{r1，r2，…，rn}对秘密信息进行加密操作，则秘密信息为

为了嵌入信息，服务运营方首先读取最高位平面的mark。根据mark值得出图像的压缩总长，以此判断最高位平面是否留有嵌入空间，具体计算为

式中，R1为最高位平面的剩余空间。

其次，通过读取第1 位至第log2(M×N× 8)位得到压缩位置图的长度ℓL，对应图6 获得Lc对应的位置和长度，用无损解压得到完整的位置图L。由于无法修改最高位平面，运营方通过替换位置图中标记为0 的像素点的前β-1 个位平面来嵌入隐秘信息。假定选取图5 像素块中第2 行第3 列像素点进行多MSB 替换，结果如图7 所示。而在位置图标记为1的像素无法进行信息隐藏，因其前β并非全为0，若替换将无法恢复原始像素。因此，可以通过式（23）得出嵌入空间，具体为

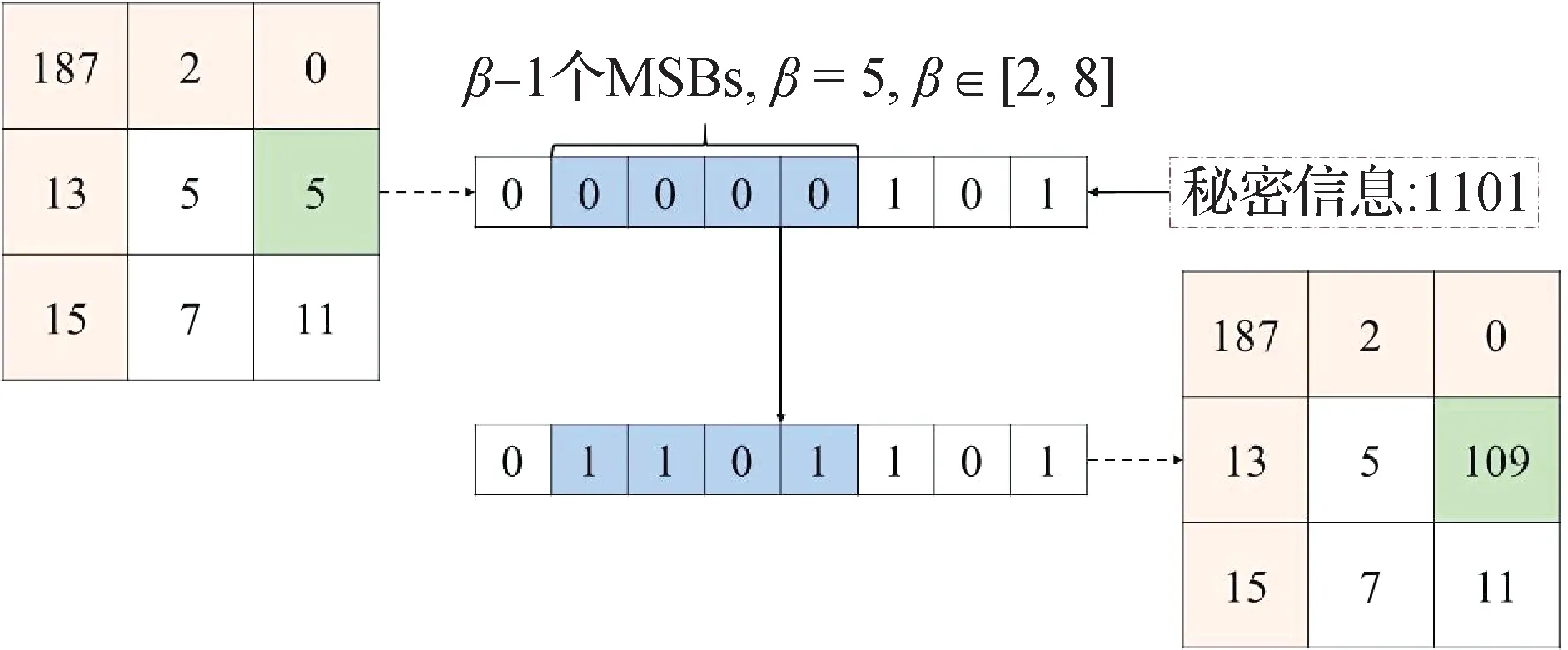
图7 信息隐藏嵌入例子Fig.7 Example of data hiding

式中，R2为次高位平面至第β个位平面之间的嵌入空间，isequal(p，q)表示当p与q相同时为1，否则为0。

2.4 信息提取与图像恢复

2.4.1 信息提取

当接收方只拥有信息加密密钥Kd时，可以在不泄露图像信息的基础上获得嵌入的秘密信息。首先从最高位平面提取辅助信息，无损解压以得到位置图对应0 的像素位置和β-1 个位平面的秘密信息。最后使用Kd对提取信息解密得到明文数据。

2.4.2 图像恢复

当接收方只拥有图像加密密钥Ke时，无法从载体图像中窥探任何关于秘密信息的数据，只能将加密图像彻底恢复为原始图像。实际上，恢复图像的操作为上述预操作的逆过程。步骤如下：

1）辅助信息提取。从最高位平面中首先读取mark位的数值，以判断是否存在符号指示图S，再参照图6 的比特流分布依次获得无损解压后的辅助信息：位置图L、最高位平面H和符号指示图S。

2）解密图像。携密的加密图像与用户的图像加密密钥Ke通过逐位异或操作得到解密图像D′，用上述辅助信息中的H替换掉解密图像的最高位平面，然后根据位置图中标记为0 的像素点，将对应位置的前β-1 个位平面替换为0，从而获得图像Dt，与3.1节中预处理后的图像Pt保持一致。

3）线性预测恢复。根据mark的不同，线性预测的恢复过程也不相同。若mark=0，将除了参考像素Dt(1，1)以外，位于首行和首列的像素Dt(i，j)转换为二进制序列。首先由第8 位平面获得二进制序列最后一个值，即其正负号，再将第1 位平面至第7 位平面的二进制值转换为十进制，即其预测误差绝对值大 小，因 此得到 正确的预测误差；否则mark=1表示在首行与首列的预测误差中存在绝对值大于127 的现象，根据符号指示图的存储位对相应位置的预测误差保持不变，除参考像素以外的其余数值执行上述操作。根据式（12）的逆处理，将预测误差还原为原始像素，得到图像Dh。

4）可变预测位平面翻转恢复。在图像Dh的基础上，通过迭代将所有从第2行第2列开始的像素全部恢复。若想获得原始图像的像素，每个位平面会在其低一位平面完全还原的基础上得到正确的二进制值。恢复过程将从第α位平面开始，当前迭代所在位平面的像素值Pk、预测像素Predk和翻转像素Invk由式（1）—式（10）计算获得。在Dh中第i行第j列的像素表示为Dh(i，j)，转换为8 个位平面，当第k(1 ≤k≤α)个位平面时，其恢复比特为

2.4.3 信息提取与图像恢复

当接收方同时拥有信息加密密钥Kd和图像加密密钥Ke时，只需按照上述步骤完成提取信息和恢复图像，因此得到无错的秘密信息与无损的原始图像。

2.5 最优化选择

由于不同的图像有不同的纹理分布，不同的迭代次数α与嵌入深度β会影响不同图像的嵌入率。因此，为了最大程度地利用图像的冗余信息，本节将对参数α与β进行分析，以此通过最优化自适应于图像本身。

完全可逆的信息隐藏要求算法保留最高位平面以用于辅助信息的存储，在该约束条件下2 ≤α，β≤8，并且α≥β，其中由二者搭配的图像处理选择共有28 类。式（22）（23）说明图像的净容量EC由两个部分组成，具体为

在相同迭代次数下，不同嵌入深度在不大于迭代次数的情况下产生的R2一致。如当α=2 时，β=2 与β=8 所得位置图是完全相同的。因此在其他辅助信息保持不变的情形下，这两类参数选择的有效载荷是相同的。以此将上述28 类选择简化为当α=β时的7类，用集合μ表示为

为了找到最优位置图，比较式（27）在不同选择下的数值大小，选择达到最高载荷的最优μ表达式为

式中，μ∈[2，8]。由于迭代次数的变化并不影响最高位平面与符号指示图的压缩量，因此式（29）只将位置图的压缩长度计入考量，同时要求总压缩量不超过第一位平面大小，否则将辅助信息占据第2 位平面将造成嵌入容量的损失。

3 实验结果与分析

本节将选取如图8 所示的6 幅灰度图像展示实验成果，主要包括4 个部分：安全性分析、预处理分析、嵌入性能与解密质量、实验比较。同时，对来自BOWS-2数据集的10 000幅图像进行通用性测试。

图8 测试图像Fig.8 Test images（（a）Lena；（b）Baboon；（c）Airplane；（d）Man；（e）Jetplane；（f）Tiffany）

3.1 安全性分析

安全性分析对加密图像来说是一个重要的评估要素，以保证本方案的安全级别达标，不存在任何利用像素相关性破解图像信息的可能性。下面给出了相关度量的指标。

1）信息熵（information entropy）。是描述信息源发生的不确定性，用以测量图像中不同像素出现概率的指标。图像的信息熵反映了图像包含的信息量大小。信息熵值越大，表明图像信息量越大，不确定性越高。对于加密图像，较高的熵值表示其像素值出现的随机性，进一步说明加密算法的有效性。信息熵在8个灰度图像中的计算为

式中，P(ε)指像素值ε在图像中出现的概率。

当图像包含δ个灰度值时，即图像每个像素值均不同，可以认为此时图像的不确定性最大，信息熵也达到最大值，为log2δ。因此，对于8 个灰度图像，信息熵的最大值为log2256=8。

2）直方图。由于加密图像的像素在允许范围中分布均匀，因此该直方图也将呈现平坦的直线状。

在实验中根据像素值在加密阶段和信息嵌入阶段的变化，把加密图像和含隐秘信息的加密图像的信息熵划入考虑范围，以每幅图像嵌入效果最佳的情况具体分析。结果如表2 所示，E0为原始图像的信息熵，E1指加密图像的信息熵，E2指含隐秘信息的加密图像的信息熵。可以看出，图像在不做任何处理的阶段可视信息较多。对BOWS-2 数据库中的10 000 幅图像同样进行了信息熵的实验，结果显示E1和E2的平均值为7.999 2 与7.999 3。图像在加密之后以及嵌入隐秘信息之后均接近8，说明两者间的像素都具有较高的随机性。

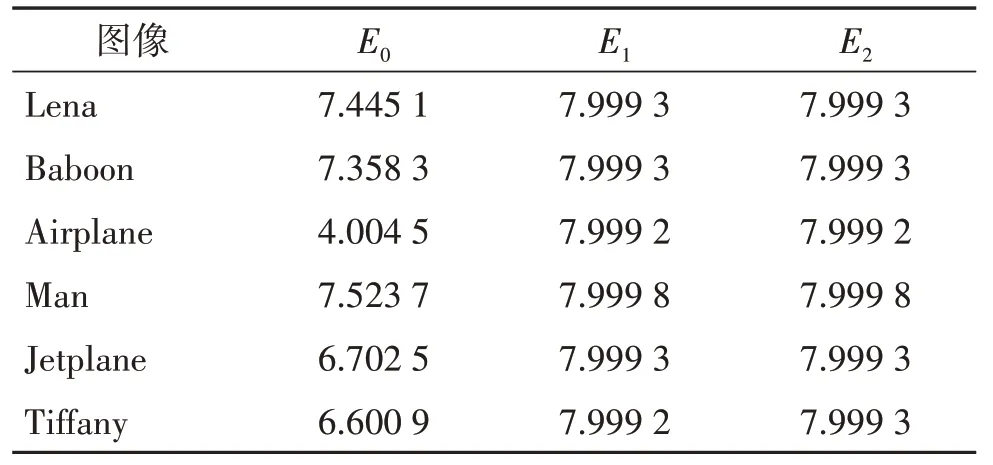
表2 本算法的信息熵比较Table 2 Comparison of entropy from the proposed scheme

一个好的加密算法不仅需要保证加密图像从视觉效果上不易察觉，而且从其数据分布情况的表现形式上也不可窥探。因此直方图也是判断该方法是否存在泄露数据风险的依据，图像在不同阶段应当显示不同的直方图分布，保证整个图像处理的过程具有安全性。以Lena 为例展示原始图像、加密图像、含隐秘信息的加密图像和恢复图像的直方图，如图9 所示。原始图像拥有不均匀分布的直方图，但在加密之后，直方图均匀分布。

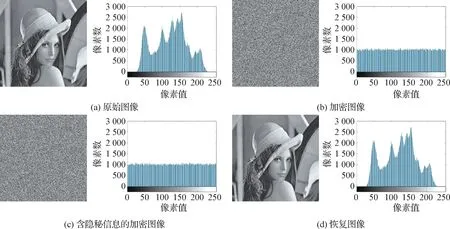
图9 Lena图像直方图测试结果Fig.9 Lena image histogram test results

3.2 预处理性能分析

本文算法的预处理为可变预测位平面翻转和线性预测，两者至关重要。其中，可变预测位平面翻转增加了位平面中0 的数量；线性预测增加了用以嵌入的像素数量。

位平面的信息熵测量用于测试可变预测位平面翻转的性能。位平面中的每一位只有可能为两个值：0 和1。假设0 出现的概率为PZ，则1 的概率为1 -PZ，那么，可以得到位平面的信息熵Eb的计算为

当1 或0 出现的概率为100%或0%时，说明位平面处在稀疏状态，不包含任何信息量，即Eb=0。当0和1出现的概率均为50%时，说明位平面中0和1的个数相同，即Eb=0.5。每个位平面相当于一个二值图像，因此其信息熵的最大值为log22=1。

在图像库中随机选择1 000 幅纹理复杂度不同的图像用于测试本算法，将其原始位平面与经过可变预测位平面翻转后的位平面计算各自熵，用散点图展示，如图10所示。其中，k=1表示最高位平面，k=8 表示最低位平面。从图10 可以看出，VPBI 使前5 个高位平面的熵大幅度减小，比原始位平面更接近于0。经过计算可知，VPBI 之后最高位平面的熵平均值为0.04，远小于原始MSB 的平均值0.76。相较于MSB 较高的相关性，第2，3，4，5 位平面像素之间的相关性则相对较低，信息熵的平均值分别为0.25，0.45，0.61，0.75，但是也低于原始熵的0.83，0.91，0.97，0.99。这说明VPBI 方法在迭代过程中使多个高位平面产生了更多的0。当然，因为低位平面的噪声，第6，7，8 的位平面熵只存在轻微的减小。

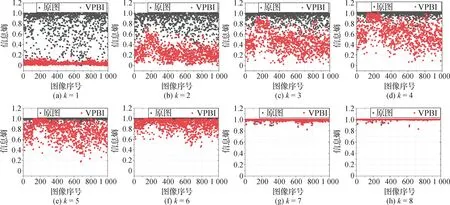
图10 位平面信息熵Fig.10 Bit-plane entropy（（a）k=1；（b）k=2；（c）k=3；（d）k=4；（e）k=5；（f）k=6；（g）k=7；（h）k=8）

在第3.1 节中，本文针对线性预测出现的特殊预测误差做标记处理，生成符号指示图，并用一个标识符mark记录该符号指示图的存在性。为说明线性预测的性能，本文通过测试10 000幅来自BOWS-2数据库的图像，在10 000 幅测试图像中，仅有643 幅图像存在符号指示图，占据比例为6.43%。这说明大部分图像的符号指示图S为全0序列，不需要作为辅助信息嵌入。

3.3 嵌入性能与解密质量

RDH-EI方案通常由以下两个参数衡量。

1）嵌入率（embedding rate，ER）。每一个像素嵌入的秘密信息的位数定义为嵌入率，则本文的嵌入率计算为

式中，EC由式（27）计算获得。

2）恢复图像的视觉效果。在可逆信息隐藏领域中，可以还原原始图像，不损失任何感知质量是一个重要的标杆。但一些研究无法做到完全恢复图像，在这种情况下，就可参考峰值信噪比（peak signal-tonoise ratio，PSNR）和结构相似性指数（structure similarity index measure，SSIM）这两个质量量度。

所提方案的嵌入率受到μ值大小的影响，结果如表3—表8所示，所有图像尺寸为512 × 512像素。由于一幅图像的最高位平面与符号指示图不受μ值大小的影响，在排除其占用空间后，不难看出，纹理度相对简单的图像，随着压缩位置图的增大，其净嵌入容量也在增加，因此μ值相对较大。例如Lena 与Airplane具有较高的嵌入率，分别为2.627 9 bit/像素和3.283 7 bit/像素。然而，纹理较为复杂的图像嵌入率较低，例如μ=3 时，Baboon 的最大嵌入率为1.219 7 bit/像素。这是因为该图像不仅存在符号指示图，辅助信息的压缩量也比一般平滑图像大。除了常用的6幅灰度图，同时测试了BOWS-2数据库的图像，所有图像的PSNR 均为∞，SSIM 等于1，说明本文算法可以无损恢复原始图像。

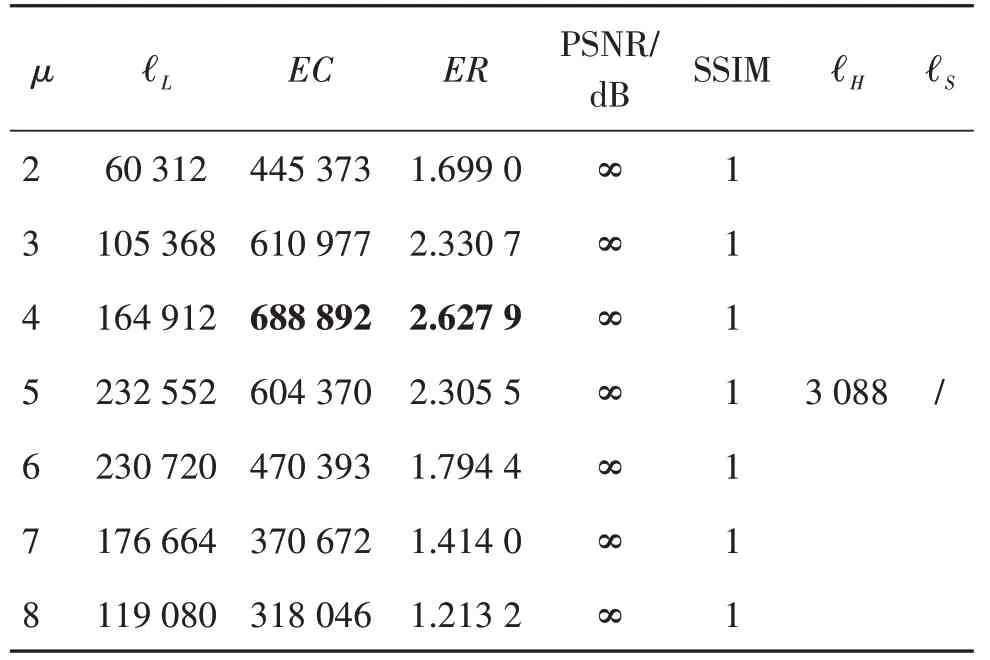
表3 Lena图像在不同μ值的嵌入容量（bit）Table 3 Embedding capability（bit）of Lena images at different μ values

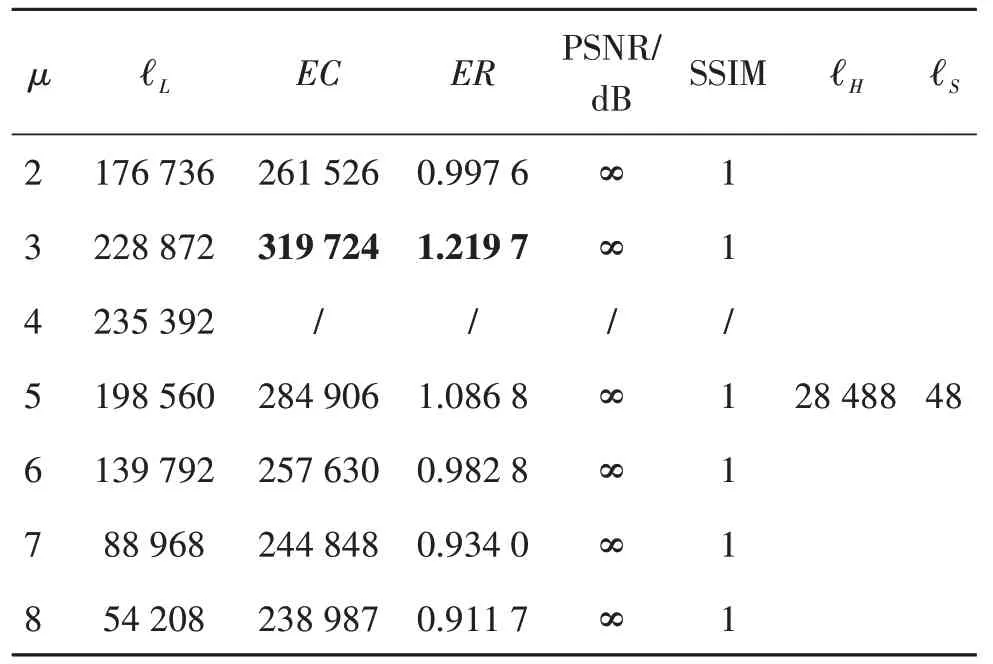
表4 Baboon图像在不同μ值的嵌入容量（bit）Table 4 Embedding capability（bit）of Baboon image at different μ values

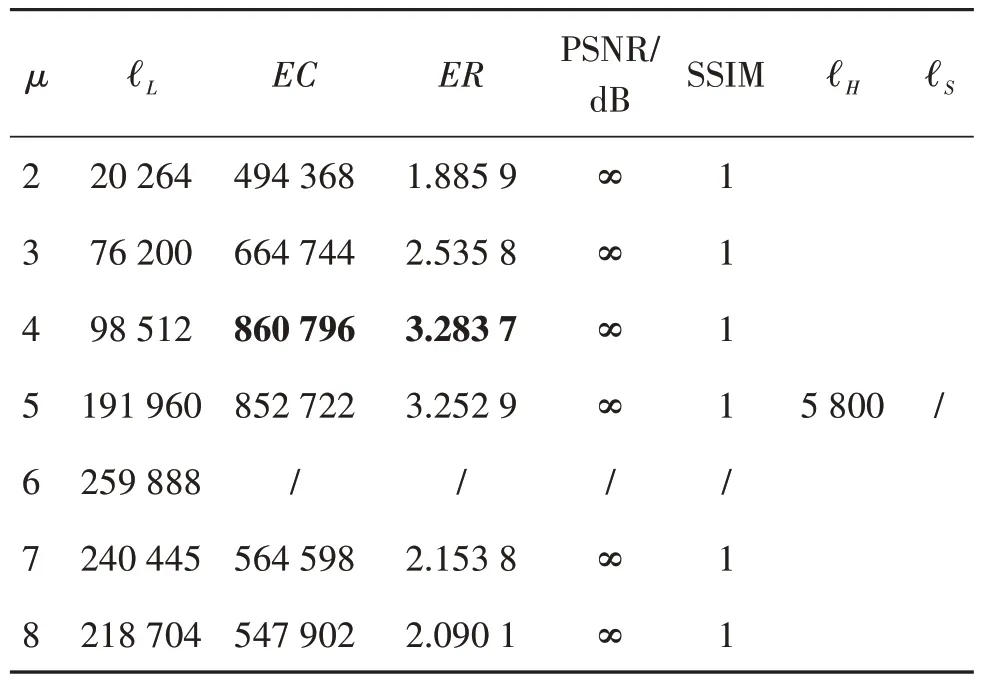
表5 Airplane图像在不同μ值的嵌入容量（bit）Table 5 Embedding capability（bit）of Airplane image at different μ values

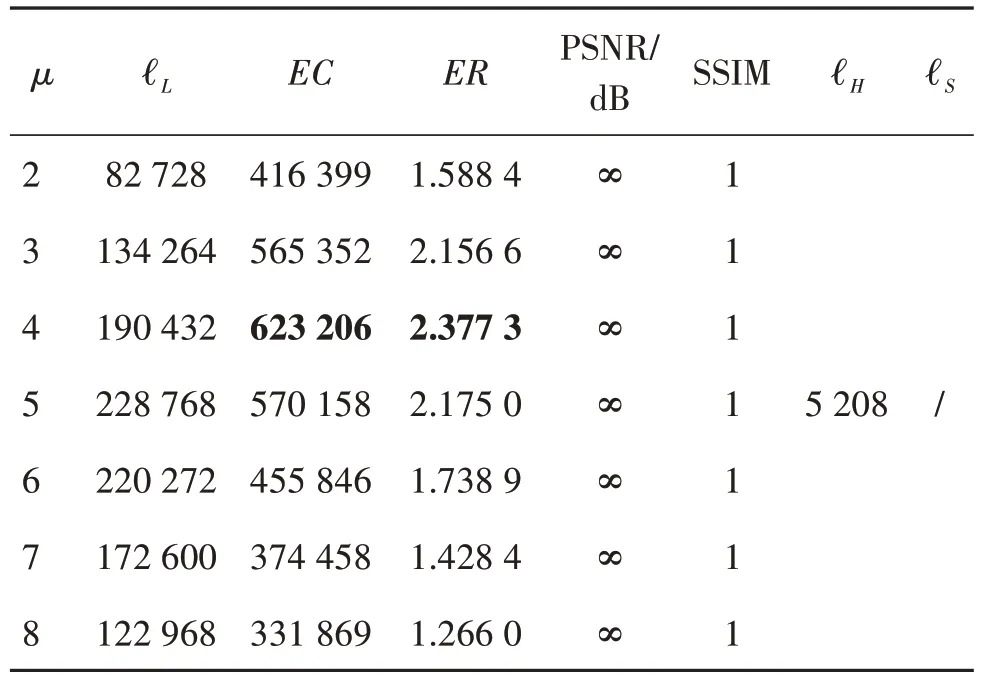
表6 Man图像在不同μ值的嵌入容量（bit）Table 6 Embedding capability（bit）of Man image at different μ values

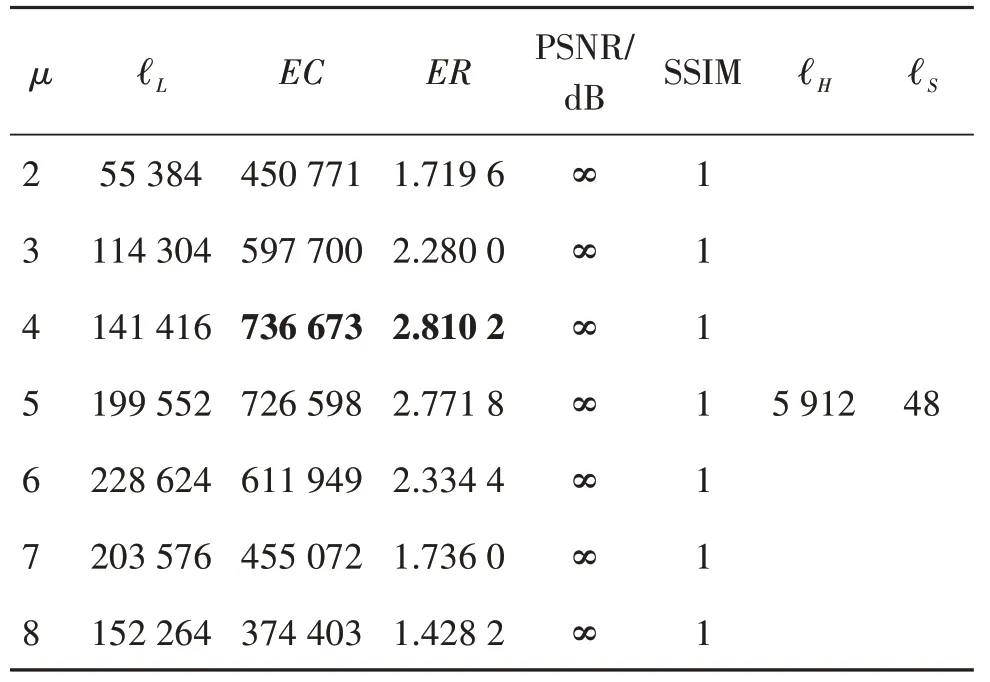
表7 Jetplane图像在不同μ值的嵌入容量（bit）Table 7 Embedding capability（bit）of Jetplane image at different μ values

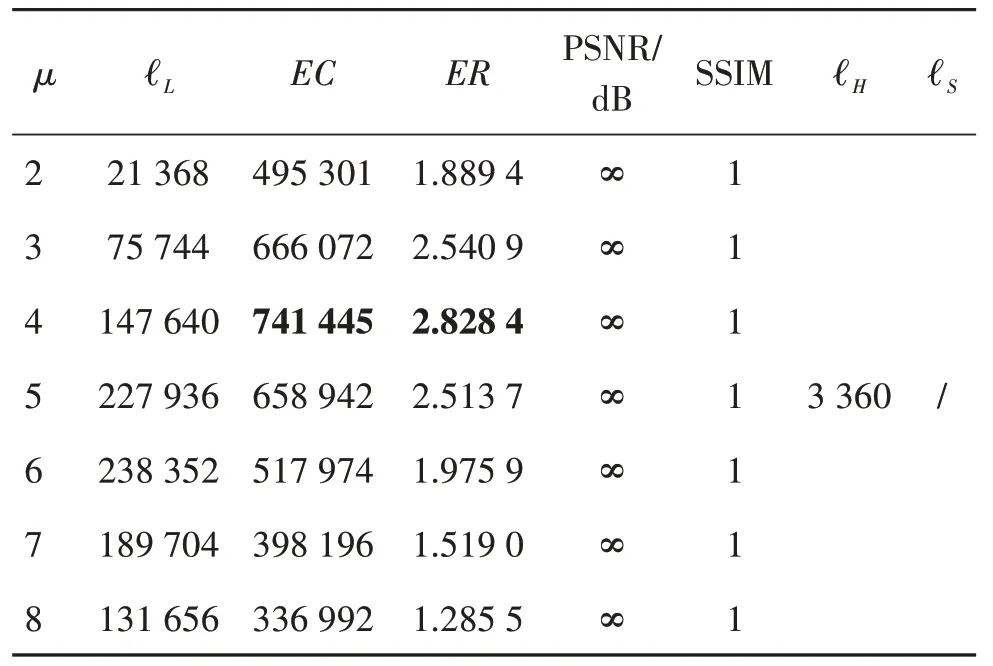
表8 Tiffany图像在不同μ值的嵌入容量（bit）Table 8 Embedding capability（bit）of Tiffany image at different μ values

3.4 实验比较

为进一步显示本文算法的优越性，本节将展示本文方法和相关方法的比较结果，选取Puteaux 和Puech（2018）、Chen 和Chang（2019）、Wu 等 人（2020）、Mohammadi 等 人（2020）、Zhang 和Luo（2022）的相关测试数据。公平起见，设置Chen 和Chang（2019）算法中的块大小为4 × 4，将Wu 等人（2020）算法的参数设置为α=5，β=2，设置Mohammadi 等人（2020）算法中的块大小为3 × 3，将Zhang和Luo（2022）算法的参数b设置为4。

以6幅常见图像为例，比较结果如图11所示，可以看出Puteaux 和Puech（2018）算法的嵌入率比较小，这是因为该算法的嵌入只涉及最高位平面。Chen 和Chang（2019）、Mohammadi 等人（2020）、Wu等人（2020）、Zhang和Luo（2022）以及本文算法涉及多个位平面，因此嵌入率较高。结果证明本文算法在6 幅测试图像中均优于现有算法，对于像素相关性较高的Airplane 图像，本文算法达到了3.284 bit/像素；对于纹理度较为复杂的Baboon 图像，本文算法容量达到了1.220 bit/像素。以上测试结果说明本文算法对像素相关性较高的图像具有优秀的嵌入能力，对纹理较为复杂的图像也能保持一个良好的嵌入率，相较于其他算法大幅度降低的嵌入率，体现出较高的优势。

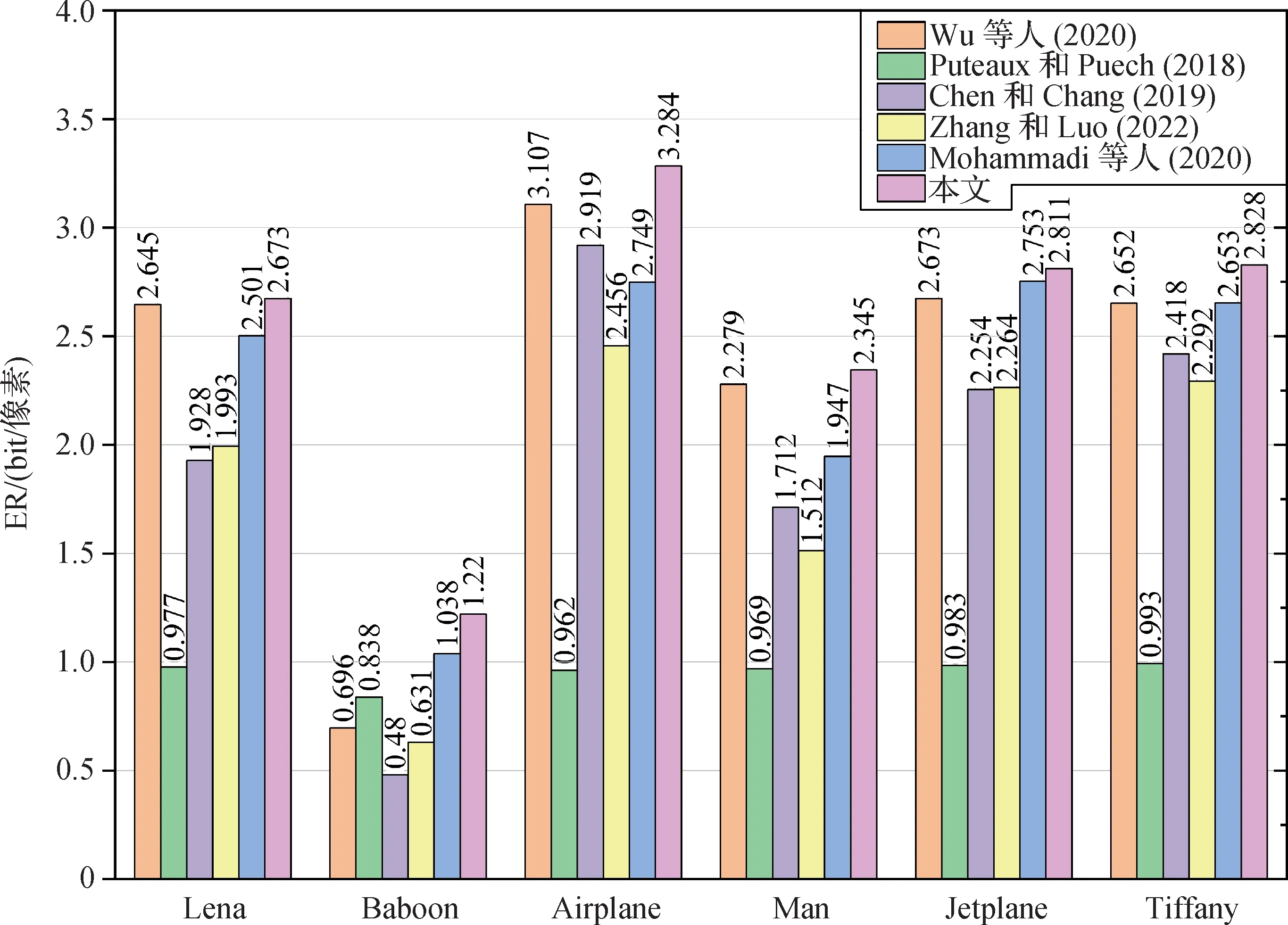
图11 不同算法的嵌入率在测试图像上的比较Fig.11 Comparison of ERs among different methods on test images

为避免偶然性，在BOWS-2 数据库对10 000 幅图像进行了测试，比较结果如图12 所示。本文算法的平均嵌入率达到了2.953 bit/像素，均高于现有算法。

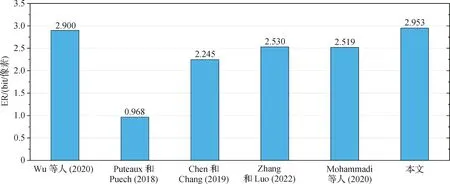
图12 不同算法在BOWS-2图像库中的平均嵌入率比较Fig.12 Comparison of ERs among different methods on BOWS-2

4 结论

本文提出了基于可变预测的密文域图像可逆信息隐藏算法。为了充分利用像素之间的冗余度，减少符号指示的空间占用，设计了可变预测位平面翻转方法。通过可变的预测值、目标像素的翻转值与目标像素进行比较，以此预留出嵌入空间。在嵌入阶段，采用多MSB替换的方法以隐藏秘密信息。将自适应位置图和其他辅助信息保存至最高位平面，保证图像持有方在向云端服务器传输图像时无需其他额外的数据。实验证明该方法有较高的嵌入率，并且可保证可逆性与安全性。然而本算法仅利用自适应位置图中标记的可嵌入像素，浪费了未被标识的像素中的冗余空间。在未来，将期望找到进一步优化高纹理图像的嵌入方案，例如采用动态值μ提升嵌入率。