考虑鲁棒成本与绝对后悔的最短路径问题研究

周和平,李文杰

(长沙理工大学 交通运输工程学院,湖南 长沙 410114)

0 引 言

交通路网的阻抗决定了两点间的最短路径,然而路网系统复杂多变,最短路径会受到交通需求、交通控制等多种因素的影响,因此它不是一个定值,而是一个动态变化的不确定值[1-2]。研究最短路径问题时考虑路网阻抗的不确定性才能更好反映交通实际情况,已有学者用区间数据来描述路网阻抗的不确定性,进行最短路径问题研究。P.KOUVELIS等[3]在使用区间数据表示路段阻抗的路网中,结合鲁棒优化方法,给出了鲁棒最短路径的定义; H.YAMAN等[4]基于区间路网提出了鲁棒成本概念,针对鲁棒最短路径问题建立了以鲁棒成本最小为优化目标的混合整数规划模型;贺剑等[5]采用区间数表示交通需求的不确定性,并引入鲁棒有效路径,构建了网约车合乘路径优化模型;谭倩等[6]考虑公交车行驶时间的不确定性,建立了基于区间阻抗的改进Logit公交客流分配模型;M. EHRGOTT等[7]提出鲁棒多目标优化问题,将鲁棒优化问题从单目标到扩展到多目标;YU Gang等[8]提出区间阻抗下的最短路径问题是NP难问题,精确算法和启发式算法是求解此问题比较常用的算法;周和平等[9]针对鲁棒最短路径模型应用分支定界算法进行了求解;陈莹等[10]提出了一种基于分层学习和差分进化的混合粒子群优化算法;D.DICAPRIO等[11]提出了一种新型蚁群算法;A .KASPERSKI等[12]提出鲁棒最短路径的多项式时间近似算法;A. B.CHASSEIN等[13]基于分支和定界框架,为最优值引入一个新的下界,并应用到鲁棒最短路径问题的求解中。

在区间路网的最短路径问题中,现有模型目标为最小化最大后悔值(即鲁棒成本),所得鲁棒最短路径是所有最糟糕情境下的最优路径,结果往往过于保守。基于此,笔者提出了一种考虑鲁棒成本和绝对后悔值的多目标最短路径模型,它既保留了鲁棒最短路径具有鲁棒性的优点,又能有效克服鲁棒最短路径过于保守的缺陷,最后为了对模型求解,设计了一种改进的Benders分解算法。

1 多目标最短路径模型

1.1 符号定义

1.1.1 定义参数

相关参数定义如表1。

表1中,下界、中值、上界最短路径分别为路网中所有路段阻抗取区间下界值、中值、上界值时的最短路径;情景最短路径为路网中所有路段阻抗已知时的最短路径。

1.1.2 定义变量

相关变量定义如表2。

1.2 鲁棒成本

区间路网下路径阻抗是一个区间数,是一个不确定值,故路径的优劣无法通过路径阻抗的大小直接进行比较,文献[4]在研究区间阻抗下的最短路径问题时,基于鲁棒偏差方法提出了鲁棒成本的概念,即路径的最大后悔值。

鲁棒成本的定义为:给定路网G=(N,L),假设从起点到终点存在一条路径p,将路径p中所有路段的阻抗取区间上界值而其他路段的阻抗取区间下界值,在此情景下起点到终点的最短路径为p*,那么,路径p的上界阻抗与路径p*的阻抗之差即为鲁棒成本,其表达如式(1):

(1)

1.3 绝对后悔值

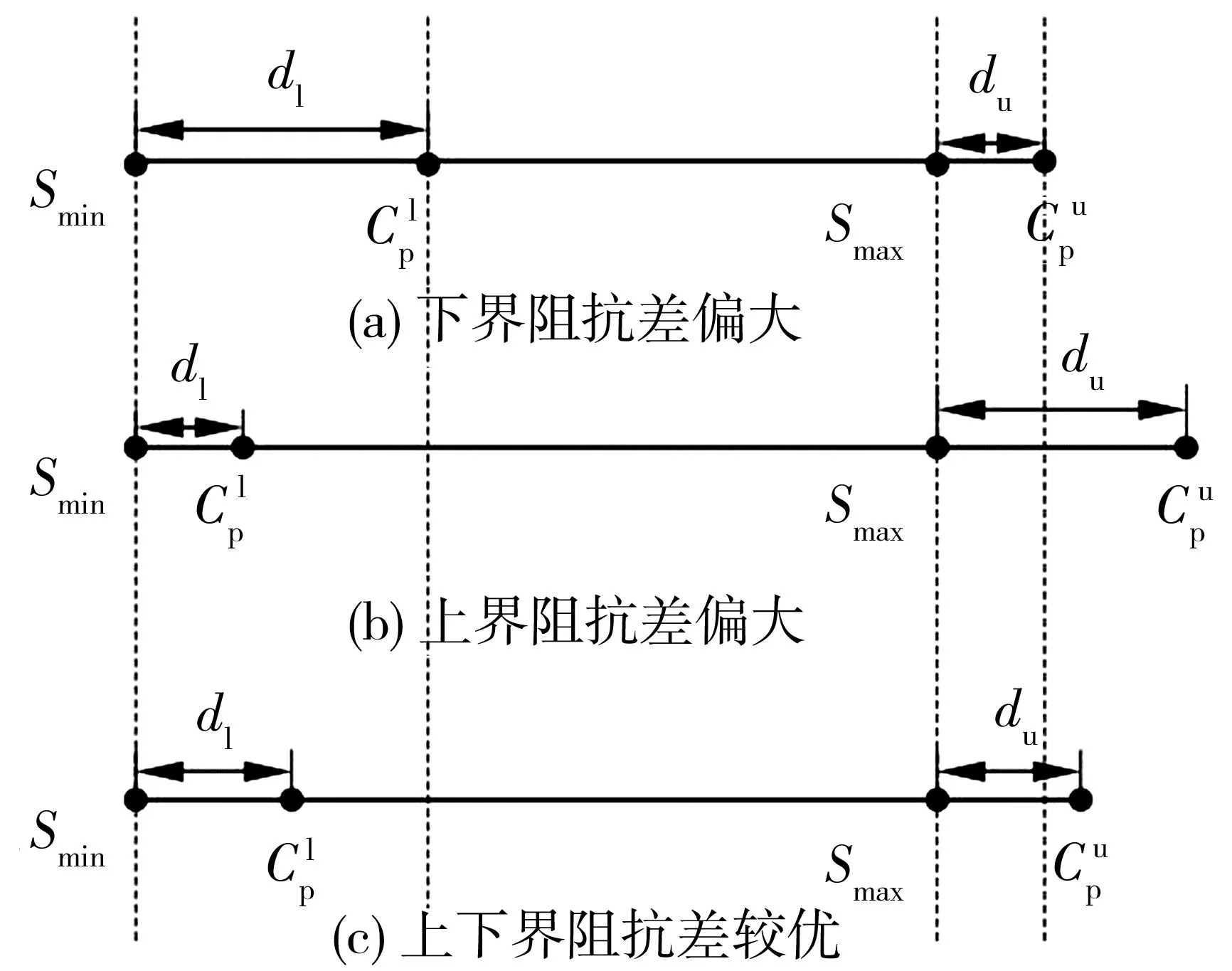
图1 上界与下界阻抗差Fig. 1 Impedance difference between upper and lower bounds

图中dl为路径下界阻抗与下界最短路径阻抗之差〔式(2)〕、du为路径上界阻抗与上界最短路径阻抗之差[式(3)]。

(2)

(3)

在已有的研究中,往往只考虑鲁棒成本,所得到的鲁棒最短路径与路网最优路径的阻抗关系如〔图1(a)〕。在路网状态较差时du较小,同时具有鲁棒性,路径较优,然而在路网状态较好时dl偏大,说明鲁棒最短路径的下界阻抗远大于下界最短路径阻抗,此时结果过于保守。

为方便理解,设计如下算例:

给定有向网络G=(N,L)如图2。对图2中点1～5的所有路径指标进行计算,计算结果如表3。由表3可知,点1～5的鲁棒最短路径为1-2-5,由于此时dl偏大为4,因此在路网状态较好时选择该路径过于保守。同样,当单独考虑du对路径选择的影响,最优路径同样是1-2-5,会出现如图1(a)的情况,即路网状态较好时,dl偏大,路径过于保守;当单独考虑dl对路径选择的影响,最优路径是1-3-5,会出现如图1(b)的情况,即路网状态比较糟糕时,du偏大,路径过于保守;同时考虑dl、du对路径选择的影响,最优路径选择是1-4-5,此时dl=1且du=1,情况如图1(c),既能保证路网在不同状态下最优路径,又不过于保守。

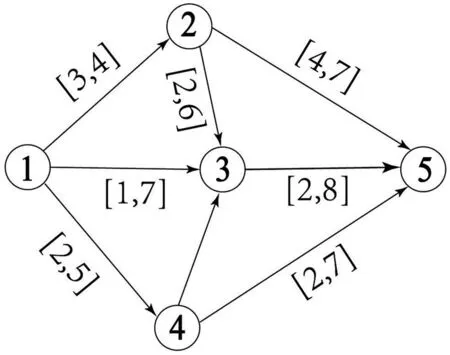
图2 有向区间路网Fig. 2 Directed interval road network

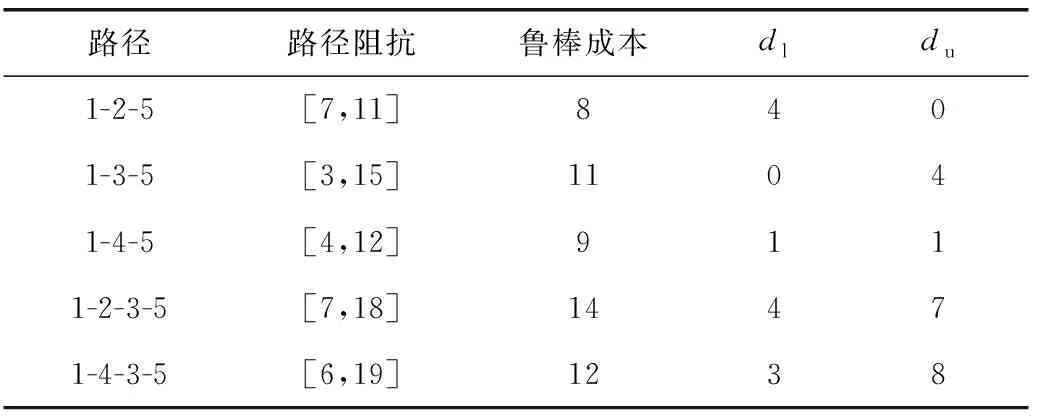
表3 1-5路径计算结果表Table 3 1-5 path calculation results

当a,b同时为区间数或者有一个为区间数时, 设a=[a-,a+],b=[b-,b+],且记la=a+-a-,lb=b+-b-,则称式(4)为a≥b的可能度公式。

(4)

将表3中的路径阻抗分别代入式(4)可知,路径1-2-5的阻抗大于1-4-5的可能性为0.583,路径1-3-5的阻抗大于1-4-5的可能性为0.55,即路径1-4-5的阻抗最小,所以笔者提出了绝对后悔值概念。

绝对后悔值的定义为:对给定路网G=(N,L),假设从起点到终点存在一条路径p,分别求路径p的下界阻抗与下界最短路径阻抗之差、路径p的上界阻抗与上界最短路径阻抗之差,并将两差之和称为路径p的绝对后悔值,如式(5)。

(5)

1.4 模型构建

1.4.1 目标函数

以鲁棒成本与绝对后悔值最小为优化目标,前者旨在保证模型最短路径的鲁棒性,后者旨在找到不会过于保守的路径,目标函数如式(6):

minWp=minλRp+(1-λ)Ap=minλ·

Smin-Smax]

(6)

1.4.2 约束条件

1)流量守恒约束

路网中所有节点上的进出流量必须满足守恒约束,不能出现流量的增减,以保证出行者从起点节点到达目标节点。

(7)

2)最短路径约束

在特定情景下从起点r到节点j的最短路径阻抗,是一个根据决策变量pij取值而变化的变量。

μrj≤μrt+lij+(uij-lij)pij,∀(i,j)∈L

(8)

μrr=0

(9)

μrj≥0,∀j∈N

(10)

3)决策变量约束

当边(i,j)在多目标最短路径模型上时,其取值为1,否则为0。当所有pij全部取值时,会得到一条由pij为1的路段所组成的路径,该路径的路段阻抗取区间上界值,其他路段阻抗取区间下界值。

pij∈{0,1},∀(i,j)∈L

(11)

根据以上多目标最短路径模型的数学模型可知:当λ=1时,目标函数不再受到绝对后悔值的影响,此时的模型等价于鲁棒最短路径模型;当λ=0时,目标函数不再受到鲁棒成本的影响,此时模型最优路径为路网的中值最短路径。

显而易见,绝对后悔值最小的路径是中值最短路径。由式(5)知:由于上界最短路径与下界最短路径的阻抗确定,因此求绝对后悔值最小的路径等价于求上界阻抗与下界阻抗之和(易知其为路径中值的两倍)最小的路径,因此绝对后悔值最小的路径是中值最短路径。

2 算法设计

多目标最短路径模型为混合整数线性规划模型,在问题规模不大时,求解比较容易,但是随着路网规模变大或引入其他约束,求解难度大大增加。根据此模型变量的特点,文献[14]设计了一种改进的Benders分解算法,将模型中决策变量pij与变量μrt分离,得到只包含决策变量pij的主问题和固定决策变量后只包含变量μrt的子问题,通过求解子问题的对偶模型,产生主问题的附加约束,再进行迭代。

2.1 子问题对偶模型

在决策变量pij已经确定情况下,得到只含有变量μrt的子问题模型,其数学模型如式(12)～式(16)。

(12)

(13)

μrr=0

(14)

μrj≥0,∀j∈N

(15)

(16)

由式(13)可知μrj实际上是经典最短路径问题的对偶形式,再次对偶即可得到经典最短路径问题的数学形式。因此只含有变量μrt的子问题模型的对偶模型如式(17)～式(19):

(17)

(18)

wij∈{0,1},∀(i,j)∈L

(19)

2.2 主问题模型

(20)

(21)

pij∈{0,1},∀(i,j)∈L

(22)

2.3 Benders分解算法步骤

Step 1：初始化。设置上界Y为+∞,下界X为-∞,计算起点到终点的上界、下界和中值最路;

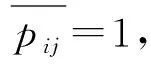
Step 5：判断Y-X是否为0,如果为0则输出最优解,停止计算,否则转入Step 6;

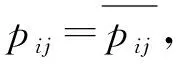
2.4 Benders分解算法改进

传统有效路径的判断依据是路径是否由有效路段组成,而有效路段的判断依据是路段下游节点是否比上游节点更远离起点同时又更接近终点[15]。这显然不适用于区间路网的情形,为此,笔者重新定义了有效路径。

由于绝对后悔值最小的路径是中值最短路径。当一条路径的鲁棒成本比中值最短路径的鲁棒成本大时,无论模型系数如何改变,该路径的目标函数必定大于中值最短路径的目标函数。有效路径定义为:鲁棒成本不大于中值最短路径的路径称为有效路径。

基于有效路径定义,在主问题中添加有效路径约束,从而加快Benders分解算法的收敛速度,有效路径约束如式(23):

(23)

3 算例分析

3.1 数据准备

以MATLAB生成的区间路网为算例,对建立的模型与设计的算法进行测试,如图3。该测试路网共有29个节点,70条双向通行路段,各路段附近的区间数为其路径阻抗。

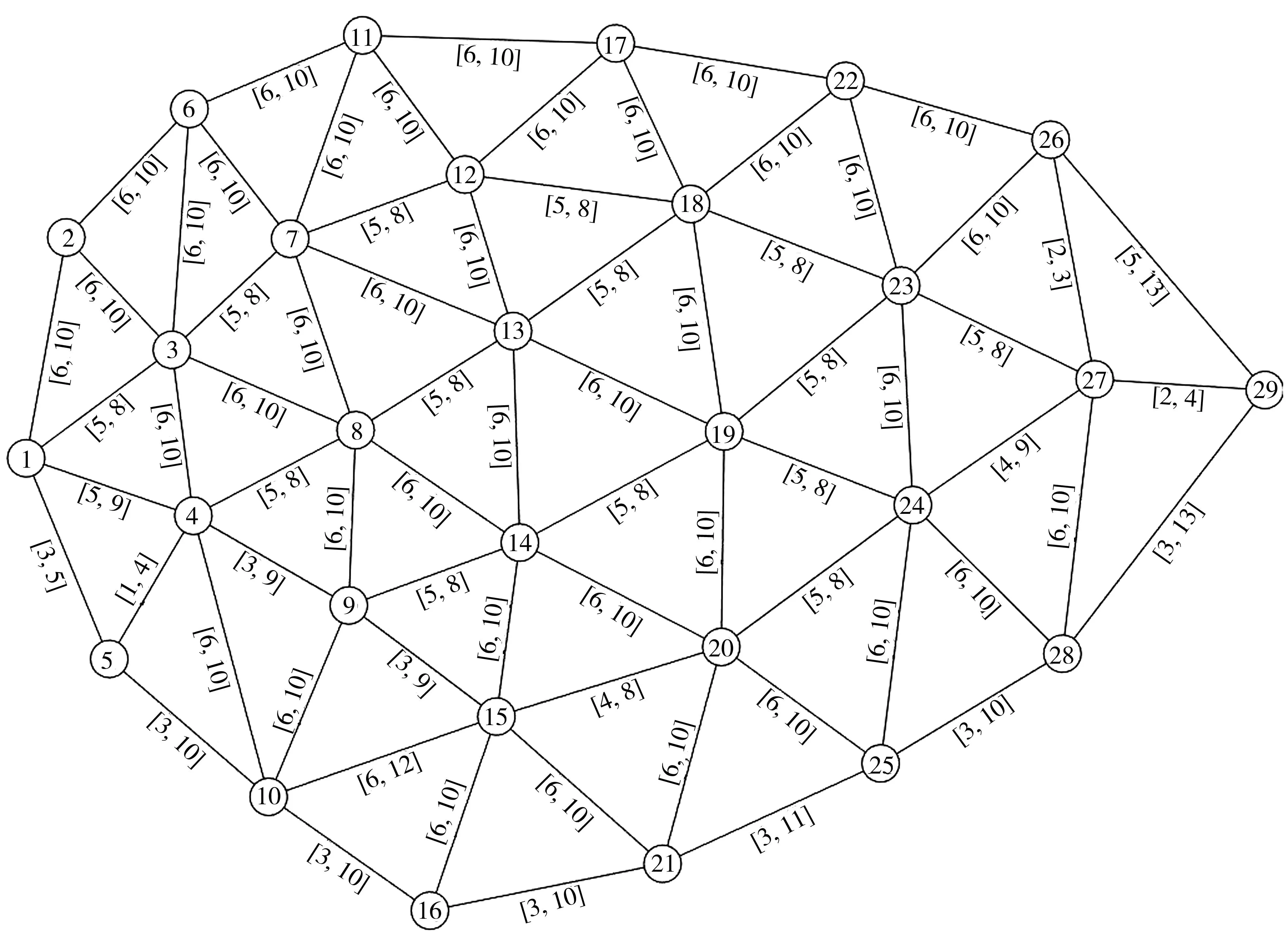
图3 测试路网Fig. 3 Test road network

由于鲁棒成本取得最小值时,多目标最短路径为鲁棒最短路径;绝对后悔值取得最小值时,多目标最短路径为中值最短路径。为了突出模型系数λ的重要性,该测试路网需要满足如下条件:路网中的鲁棒最短路径与中值最短路径为不同路径,若为同一条路径,模型系数λ将对多目标最短路径的选取没有任何影响。

3.2 结果分析

通过Python语言对算法求解,算法中的主问题模型以及子问题模型的求解均采用GUROBI求解器,相关计算结果如表4、图4。

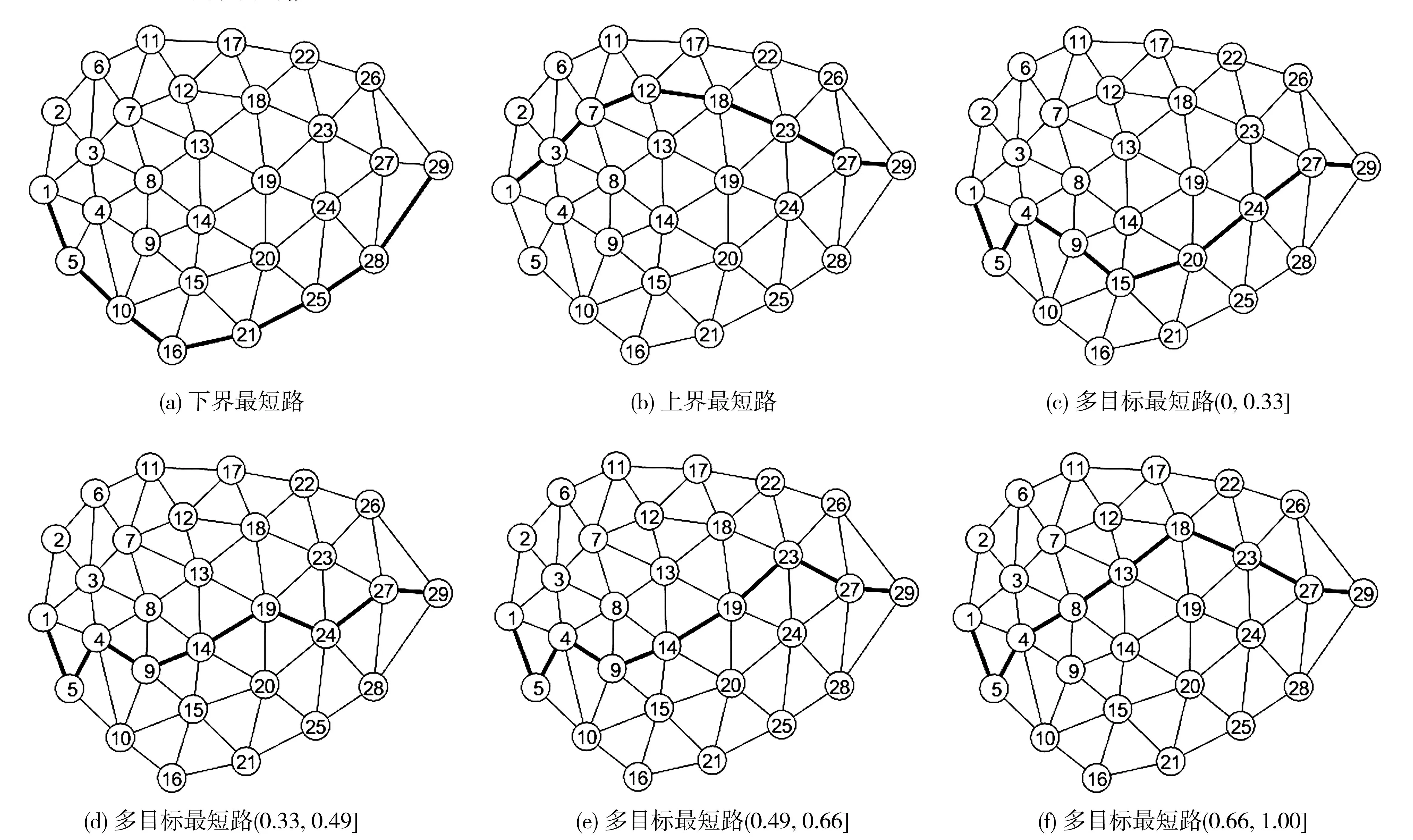
图4 1-29的最短路径Fig. 4 Shortest path map of 1-29

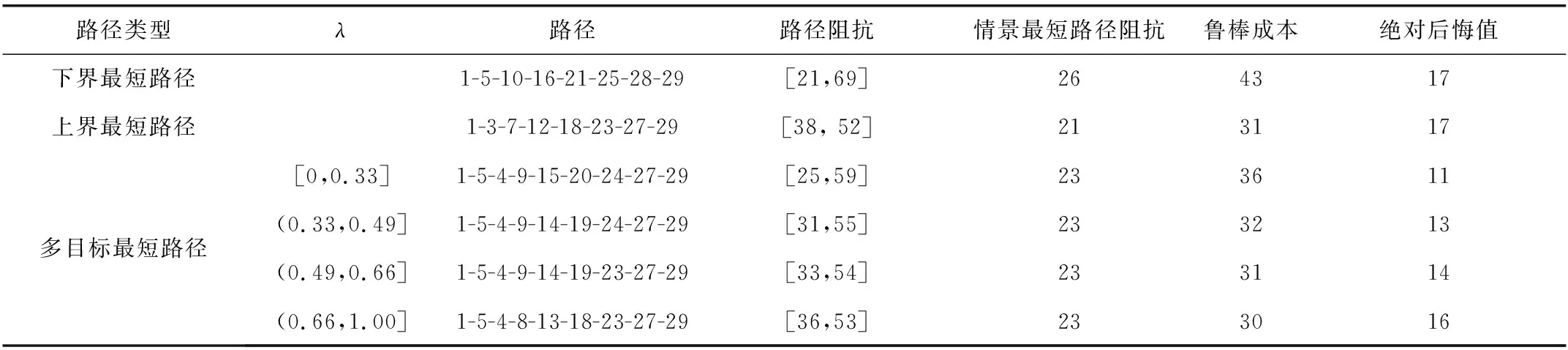
表4 1-29的最短路径径计算结果表Table 4 Calculation results for the shortest path of 1-29

由表4、图4可知:在测试区间路网最理想情景下,采用传统最短路径算法--Floyd算法,求得1-29的下界最短路径为1-5-10-16-21-25-28-29〔图4(a)〕;在路网最糟糕情景下,采用相同算法求得1-29的上界最短路径为1-3-7-12-18-23-27-29〔图4(b)〕。但上、下界最短路径只能在路网极端情景下取得最优,且路径阻抗的波动性较大,缺乏鲁棒性。

对于多目标最短路径,采用设计的改进Benders分解算法,当λ∈[0,0.33]时,求得多目标最短路径 (即中值最短路径)为1-5-4-9-15-20-24-27-29〔图4(c),记为p1〕;当λ∈(0.33,0.49]时,求得多目标最短路径为1-5-4-9-14-19-24-27-29〔图4(d),记为p2〕;当λ∈(0.49,0.66]时,求得多目标最短路径为1-5-4-9-14-19-23-27-29〔图4(e),记为p3〕;当λ∈(0.66,1]时,求得多目标最短路径 (即鲁棒最短路径)为1-5-4-8-13-18-23-27-29[图4(f),记为p4]。

当λ从0到1取值时,依次得到不同的多目标最短路径(p1,p2,p3,p4),区间阻抗分别记为r1,r2,r3,r4,将路径阻抗分别两两代入可能度公式(4)计算可得可能度矩阵〔式(24)〕,根据可能度矩阵可知:r1≤r2≤r3≤r4。

(24)

对于p1,其路径的区间阻抗虽然最小,最不保守,但是其鲁棒成本最大,路径阻抗的波动较大,与其他3条路径相比鲁棒性最弱。对于p4,其鲁棒成本最小,且路径阻抗的波动较小,具有极强的鲁棒性,但其绝对后悔值和路径阻抗偏大,过于保守。对于p2、p3,这两条路径与p4相比,鲁棒成本相差不大,且路径阻抗波动较小,因此具有较强的鲁棒性;其次,由于r1≤r2≤r3≤r4,所以路径p2、p3的路径阻抗比p4小。综上,p2、p3相比p1具有更强的鲁棒性,相比p4具有更小的路径阻抗,故路网一般状态下p2、p3优于p1、p4。

为了进一步验证Benders分解算法的求解效率,选取了5组不同的起终点,并令λ=0.5计算了它们的多目标最短路径径,同时给出了计算500次所花费的平均时间,结果如表5。计算结果表明,设计的算法能够在较短时间内准确计算出区间路网的多目标最短路径。

表5 多目标最短路径径计算结果表Table 5 Multi-target shortest path calculation results

绘制λ=1时,节点1-29的算法迭代过程如图5。由图5可知,Benders分解算法在刚开始迭代时,能较快缩小求解范围,经过6次迭代即收敛并得到最优解,说明该算法求解高效。

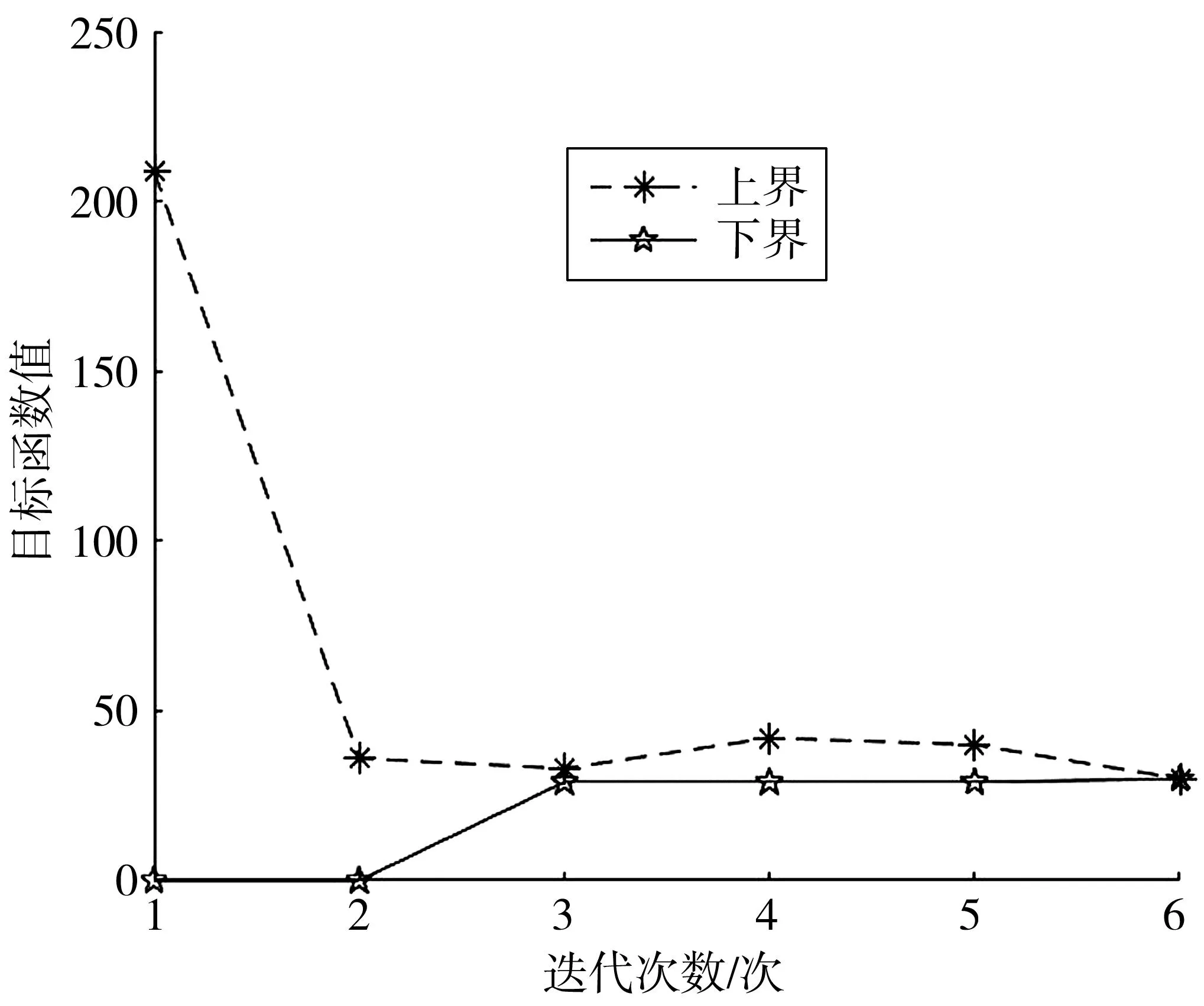
图5 算法迭代过程Fig. 5 Algorithm iteration process

4 结 论

1)在用区间数据表示路段阻抗的交通路网中,基于实际算例分析鲁棒最短路径过于保守的原因,首次提出路径决策的绝对后悔值概念。

2)采用鲁棒成本与绝对后悔值为效用指标,构建多目标最短路径模型。并基于模型特点,重新定义了适用于该模型的有效路径,增加有效路径约束,进而设计出改进的Benders分解算法,以保证在较短时间内及经过较少的迭代次数求得模型的最优解。

3)基于鲁棒最短路径模型的缺陷,增加绝对后悔值作为效用指标,有效解决了鲁棒最短路径过于保守的问题,为区间路网的最短路径问题研究提供了新思路、新方法。