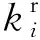基于公交优先的干线协调信号控制改进模型

赵 欣,李 瑞,酆 磊

(武汉理工大学 交通与物流工程学院,湖北 武汉 430063)

0 引 言

随着社会的发展和城市化建设,交通拥堵问题日益严重,尤其是在大城市中心区域,带来了出行时间增加、交通事故频发等一系列问题,干线协调信号控制策略应运而生。该策略通过对城市干线多个连续交叉口进行协调控制,使大多数车辆在干线不停车行驶,从而有效降低停车次数和延误,提高主干道行驶速度和整个路网的通行效率。

J.T.MORGAN等[1]是最早研究协调信号控制的专家,并首次提出了“最大带宽”的概念,此后,LU Shoufeng等[2]为解决MAXBAND模型所有车辆速度一致的问题,将交通流扩散模型与MAXBAND模型结合;陈宁宁等[3]基于MAXBAND模型建立了动态红灯排队消散时间与相位差的函数关系,增加了有效绿波带宽。

MAXBAND模型的局限性在于未考虑每个路段的交通流量和交通容量,从而导致绿灯时间需求与供应不匹配,生成的绿波带无法提供最佳性能。

因此C.STAMATIADIS等[4]将MULTIBAND扩展至干线网络,提出了MULTIBAND-96模型;唐克双等[5]取消了MULTIBAND绿波中心线的限制并增加了绿波所在位置的约束条件,提高了绿波的稳定性;ZHANG Chao等[6]提出了AM-BAND模型,与MULTIBAND相比能够得到更大的带宽;ZHOU Hongmin等[7]提出了一种非均匀双周期绿波优化模型,从而实现大型交叉口与小型交叉口的协调控制;常玉林等[8]将干线相交道路的左转相位纳入协调相位进行控制,降低了干线延误;赵欣等[9]针对相邻连续T型路口非直线路径的协调控制进行了研究。

MAXBAND模型与MULTIBAND模型是为解决社会车辆的信号协调控制而设计的,并不能适用于公交车辆,因为公交车辆需要进行站台停靠,且速度范围与社会车辆有所差异。Y.JEONG等[10]将有轨电车与MAXBAND模型结合,提出了一种有轨电车信号优先模型,从而有效降低有轨电车停车次数与延误;周洋帆等[11]以延误和饱和度为约束条件,在考虑有轨电车长度和公交信号优先的条件下,探讨了AM-BAND模型对有轨电车的适用范围;MA Wanjing等[12]提出了一种可分段的多带宽模型PM-BAND,同时对社会车辆和公交车辆进行协调信号控制;强添纲等[13]结合MAXBAND模型与绿灯延长策略,对公交车辆进行了优化;K.FLOREK[14]在AM-BAND模型上加入了公交车辆约束,同时为社会车辆与公交车辆提供绿波带宽;欧诗琪等[15]以网联公交为前提,在保障社会车辆干线协调控制的条件下降低公交车辆在交叉口的停车率。

笔者结合干线协调信号控制已有的研究,将干线协调信号控制模型与公交信号优先控制策略结合,在无公交车到达或公交车能够顺利通过交叉口时,提供社会车辆绿波,保证社会车辆的通行效率,在公交车辆需要在交叉口停车等待时,利用公交优先策略增加干线绿灯时间,同时为干线的社会车辆和公交车辆提供绿波,增加公交车辆不停车通过交叉口的概率,降低人均延误,实现社会车辆与公交车辆通行效益的最大化。

1 问题描述

干线协调信号控制模型主要有MAXBAND与MULTIBAND模型,这两种模型都是在每个交叉口信号配时固定的情况下,改变各交叉口的相位差和放行方式,达到让社会车辆在绿灯时间内连续通行的效果。在这种控制策略下,公交车辆被迫与社会车辆共享一条绿波带,而实际情况中,公交车辆与社会车辆的速度存在较大差异,且公交车需要进行站点停靠,导致公交车难以在绿灯时间内通过交叉口。

传统的公交控制策略以单点交叉口作为研究对象,考虑了红灯早断、绿灯延长和插入相位3种控制策略,其优先的本质是压缩非公交相位绿灯时间,延长协调相位的绿灯时间,增加社会车辆的延误的同时降低公交车辆的延误,保证人均延误更小。在饱和度较高且公交车辆较多的城市干线,将频繁使用公交优先控制策略,极易影响社会车辆正常通行,甚至造成拥堵。

因此,研究的问题可以归纳为:将协调信号控制模型与公交优先策略结合,在保证社会车辆绿波带宽的同时,给予公交车辆更大的绿波带宽,使公交车辆尽可能在绿灯时间内通过交叉口,并尽可能减小公交优先策略对社会车辆的影响。

2 模型建立

建立了一种基于公交优先的干线协调信号控制模型。该模型为混合整数线性规划模型,可以通过LINGO,MATLAB等软件进行求解。其约束条件主要可分为两个部分,第一部分为社会车辆的带宽约束,此约束保证该模型在任何时候都能够为社会车辆提供充足的绿波带宽;第二部分为公交车辆的带宽约束,此约束在公交车辆无法以原有信号相位不停车通过交叉口时,通过红灯早断或绿灯延长策略生成一条公交车辆绿波,从而减小公交车辆的延误和停车次数,保证公交车辆的通行效率。

设干线上有n个交叉口,且均为十字交叉,将第i个交叉口记为Si,则模型中对应的变量和含义如表1。

表1 模型变量Table 1 Variables of model

2.1 目标函数

由于公交车载客人数远大于社会车辆,因此笔者希望在绿波带内通过更多的乘客而非更多的车辆。传统MULTIBAND模型以车流量与道路饱和流率之比作为绿波带宽权重,未考虑公交车与社会车辆载客量的差异。根据主干道社会车辆与公交车辆的车流量和载客人数确定该绿波带宽权重,以加权后的绿波带宽和的最大值作为优化目标。

则改进后的目标函数可表述为:

(1)

带宽权重可表示为:

(2)

2.2 排队清空时间

传统的MULTIBAND模型将τi定义为交叉口的排队清空时间,但并未对此参数具体计算方法进行定义。

对于Si+1上行方向,其直行车道在一个周期内的排队车辆数等于Si支路汇入的转向车流中直行车流的比例,即:

(3)

对于排队车辆,设绿灯启亮时以饱和流率消散,可以得到:

(4)

式中:t0为启动损失时间,文中取3 s。

2.3 社会车辆约束

传统MULTIBAND模型需要保证绿波带沿中心线对称,极大地限制了带宽。笔者沿用AM-BAND设定取消了中心线,引入变量b′i与b″i,则社会车辆约束为:

(5)

模型时距图与参数如图1。

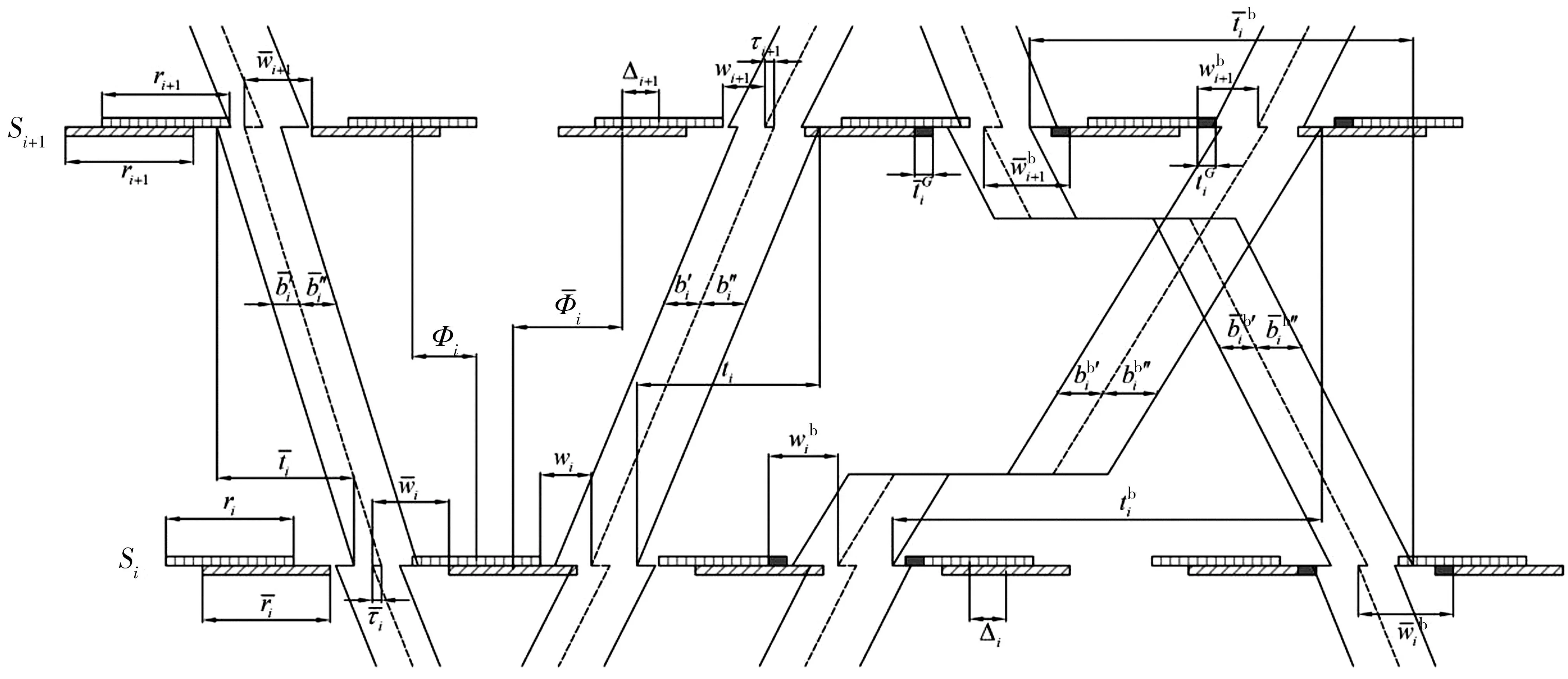
图1 改进模型时距Fig. 1 Time interval of the improved model

对于城市干道,其早晚高峰时段车流具有一定的潮汐性,上下行流量往往相差较大,为保证流量较大方向能够协调更大的带宽,添加约束条件:

(6)

(7)

为确保分隔线左右两侧的带宽处于一个合适的范围内,添加约束条件:

(8)

传统MULTIBAND模型未考虑绿波带在绿灯时间内的位置,若求解带宽较小且靠近绿灯末期,则队尾车辆有较大概率需停车等待下一周期绿灯,导致延误大大增加。因此,理想带宽分隔线应位于整个绿灯时间的前中期,使绿灯时间更大程度得到利用,则有:

(9)

(10)

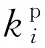
由于不同路段流量的差异导致权重因子的不同,流量较小路段对应的带宽可能被极大压缩甚至出现零带宽,使绿波中断。因此笔者引入最小带宽约束,防止出现过小的绿波带宽,保证在绿灯时间内能够通过一定比例的车辆,则有:

(11)

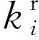
路段行驶时间应与车速范围相匹配,则有:

(12)

根据MULTIBAND基本模型,可建立社会车辆约束:

(13)

(14)

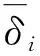
2.4 公交优先控制策略

对于信号单点控制交叉口,共有3种公交优先策略:红灯早断,绿灯延长和插入相位。前两种策略红灯早断与绿灯延长不会改变相序和周期长短,因此使用较为广泛。绿波协调控制需保证交叉口信号周期相同,因此考虑对主干道直行车流实施红灯早断和绿灯延长控制策略。

典型十字交叉口在非对称车流下有4种放行方式,如图2。

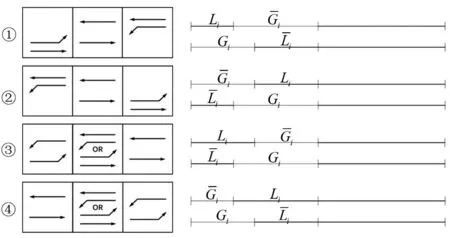
图2 相位放行方式Fig. 2 Phase release mode

不同放行方式会影响模型0-1变量取值如表2。

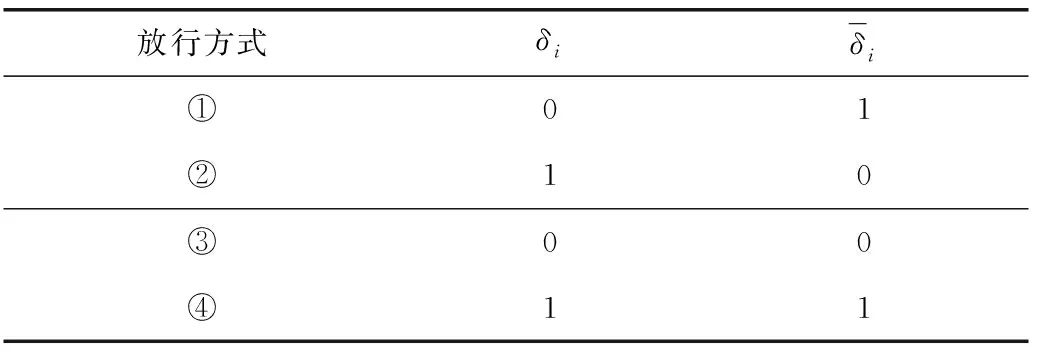
表2 不同相位放行方式下δ取值Table 2 Values of δ under different phase release modes

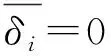
实施红灯早断和绿灯延长后将会压缩其对向左转车辆的绿灯时间。压缩后左转相位的绿灯时间需保证车辆不会二次排队,即在红灯期间内排队的左转车辆应在绿灯时间内被清空,则最短绿灯时间可表示为:

(15)

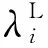
上行方向直行相位可增加的绿灯时长即为下行左转相位可以压缩的相位时长,即:

(16)

设公交车辆检测器与Si停止线的距离为Di,当公交车通过检测器时,计算公交车到达交叉口的时间范围。

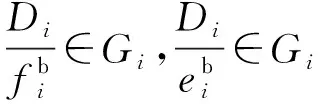
(17)

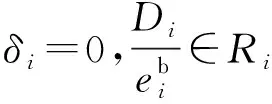
(18)

式中:Gi为绿灯相位区间范围;Ri为红灯相位区间范围;R0为检测时间与红灯终点的时间间隔;G0为检测时间与绿灯终点的时间间隔。

2.5 公交车辆约束

与社会车辆类似,公交车辆带宽约束为:

(19)

(20)

公交车在交叉口间的行驶时间包含停靠站点的时间,因此其行驶时间约束与社会车辆有所差异。

(21)

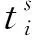
结合图1几何关系,公交车辆带宽需要被控制在实施公交优先策略后的绿灯时间内,则可建立公交车辆约束:

(22)

社会车辆红灯中点偏移量关系为:

Φi+0.5ri+1+wi+1+τi+1=0.5ri+wi+ti

(23)

同理,可推导出公交车辆红灯中点偏移量关系为:

(24)

由图1几何关系可建立公交车辆约束:

(25)

(26)

联立式(23)～式(26),可以得到:

(27)

(28)

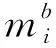
两类车辆的偏移量应相差整数个周期,即:

(29)

联立式(23)、式(24)、式(29),则有

(30)

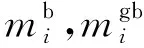
对于所有表示时长的变量,不能取负值。

3 模型验证

3.1 数据选择

笔者选取武汉市友谊大道4个连续的十字交叉口进行模型求解和仿真验证,其中东西方向为道路干线,共有8条公交线路经过,规定自西向东为上行,自东向西为下行,其直行车道为两条,左转和右转车道各一条,其余进口道均为左直右各一条车道。交叉口1,2,3,4之间的距离分别为370、350、500 m,公交站点分布如图3,各进口道社会车辆与公交车辆的流量如表3和表4。

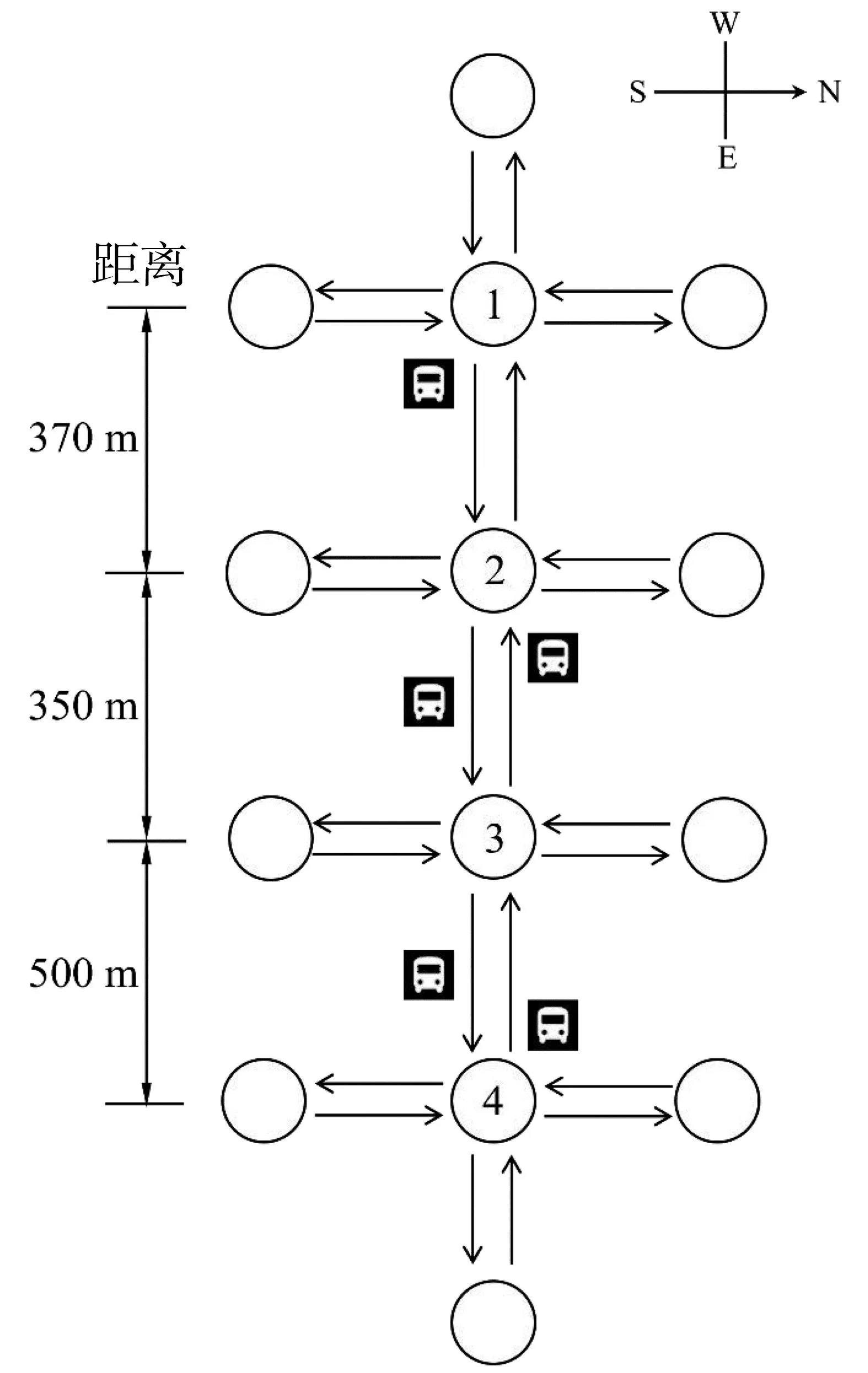
图3 选取交叉口与公交站点示意Fig. 3 Diagram of the selected intersections and bus stops

表3 各交叉口社会车辆流量Table 3 Flow of social vehicles at each intersection Pcu/h

表4 各交叉口公交车辆流量Table 4 Flow of public transportation vehicles at each intersection Pcu/h

设车道饱和流率为1 800 pcu/h,社会车辆平均载客2人,公交车辆平均载客30人,公交车停靠平均损失时间为20 s。主干道社会车辆的限速为60 km/h,因此设置社会车辆的车速在区间10～16 m/s内,公交车辆的车速在区间8～12.5 m/s内,相邻路段的速度变化范围在2 m/s内。

3.2 模型求解

根据调查数据可知,该干线高峰期的饱和度在[0.76～0.81]区间内,根据韦伯斯特模型计算,其相应的周期时长应控制在[97,122]区间内。将数据代入MULTIBAND、AM-BAND模型和笔者改进后的模型中进行求解,最优周期为122 s,带宽求解结果见表5。

表5 不同模型带宽求解结果Table 5 Solution results of bandwidths for different models s

MULTIBAND模型总带宽为240 s,AM-BAND模型总带宽为261 s,笔者改进后模型社会车辆总带宽为261 s,公交车辆总带宽为172 s。模型带宽时距图如图4。

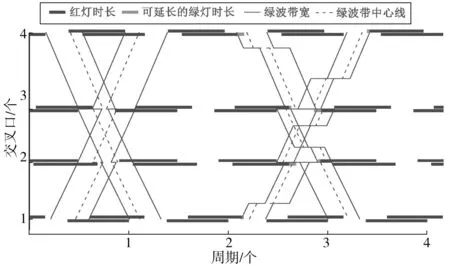
图4 文中模型带宽时距Fig. 4 The bandwidth time interval of the proposed model

3.3 仿真验证

为验证模型的有效性,以VISSIM作为仿真平台,将3种模型分别进行仿真实验验证,并对实验结果进行分析。在保证公交车辆上下行车流比的情况下,改变公交车辆的发车间隔,选取平均排队长度、车均延误时间、停车延误时间、平均停车次数、人均延误时间5个指标对3种模型进行分析,验证笔者提出模型在不同公交流量下的有效性,实验结果如表6、表7。

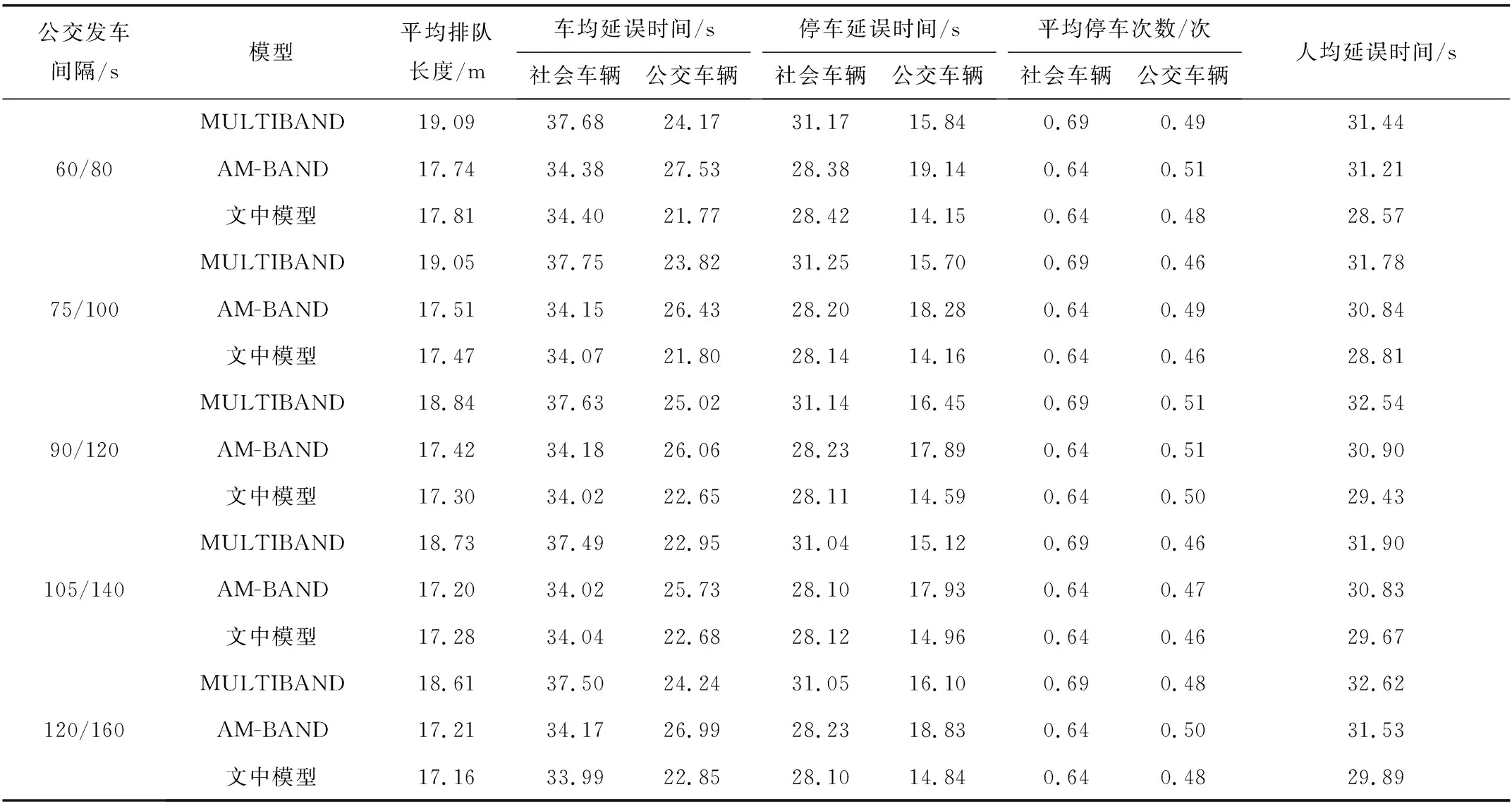
表6 仿真结果Table 6 Simulation results

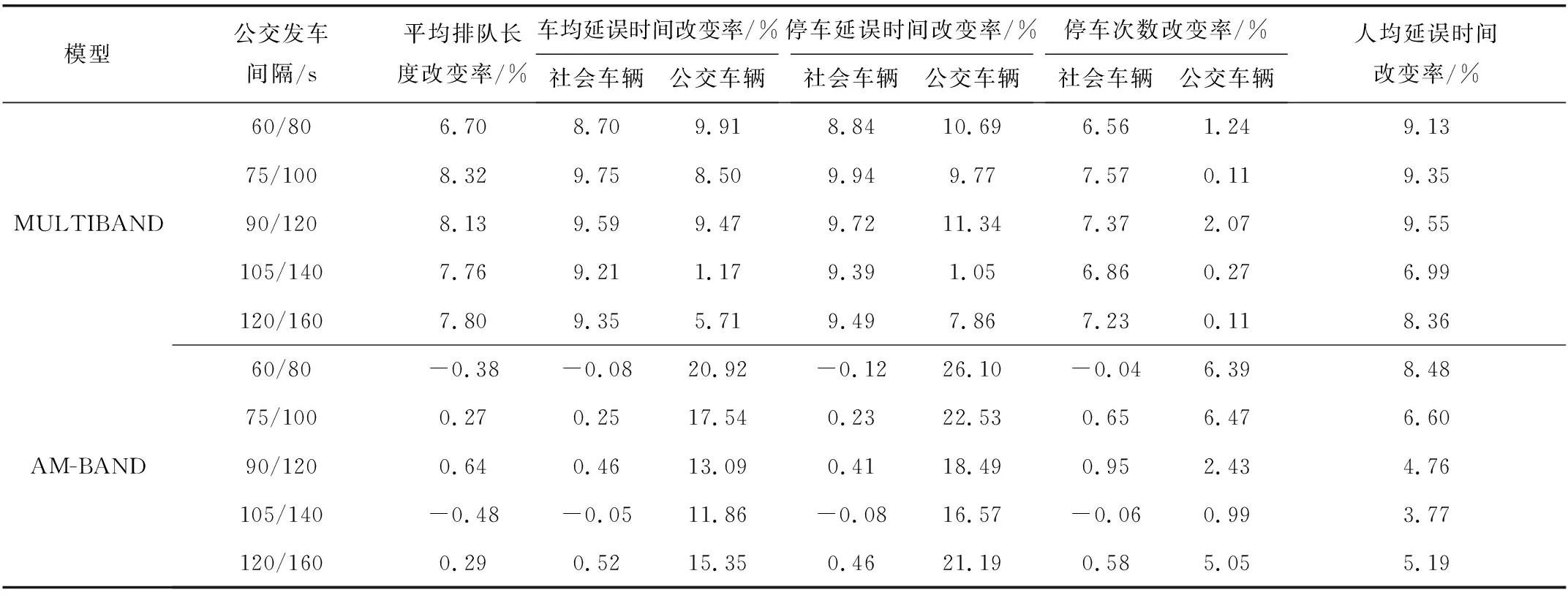
表7 文中模型与传统协调控制模型性能对比Table 7 Performance comparison between the proposed model and the traditional coordinated control model

由表6和表7可以看出,在同样的公交发车频率下,文中模型与MULTIBAND模型相比,各指标均有不同程度的优化,其中,社会车辆平均延误降低了9.32%,停车次数降低了7.12%,公交车辆平均延误降低了6.95%,平均排队长度和人均延误时间分别降低了7.74%和8.67%;与AM-BAND模型相比,其社会车辆指标相差不大,波动均在1%以内,公交车辆的延误降低了15.75%,停车次数降低了4.26%,人均延误降低了5.76%。其原因在于,对公交车辆而言,优先策略能显著减少其在交叉口停车的概率,因此与其他模型相比公交车辆各指标均有不同程度的提升;对于社会车辆而言,公交优先策略的本质在于增加相位的绿灯时长,不仅能让干线公交通过交叉口,也为干线的社会车辆增加了绿时,从而减少了干线直行的延误,弥补了干线左转车辆延误略微增加的影响,因此与AM-BAND相比社会车辆各指标几乎不变。当公交发车频率增加时,文中模型相对于传统模型,公交车辆各指标性能呈上升趋势,社会车辆的指标与AM-BAND持平,说明笔者所提出的模型在不同公交流量下都能有较好的改善效果,且对高公交流量下的道路干线具有较好的性能,进一步证明了文中控制方法的优越性。当发车间隔小于60 s时,公交车辆有极大概率在交叉口停车等待,需要频繁使用红灯早断和绿灯延长策略,干线左转相位的绿灯始终以最短绿灯时间放行,导致左转方向的排队车辆过多,造成拥堵,从而影响交叉口通行效率。综上所述,与传统协调控制模型相比,文中模型能够在保证社会车辆效率的同时,提高干线公交的运行效率,且能够较好地适应不同流量下的干线公交。

4 结 语

提出了一种考虑公交信号优先策略的干线协调信号控制模型,该模型能够对社会车辆和公交车辆带宽进行同步优化,在不影响社会车辆通行效率的情况下对公交车辆实施信号早断与延长,增大公交车不停车通过交叉口的概率。

仿真结果表明,与两种传统协调信号控制模型相比,该模型能够在保证社会车辆效率的情况下有效降低公交车辆的延误和停车次数,从而提高整个路网通行效率和人均延误,且在不同公交流量下都有较好的优化效果。