综述中学勾股定理的证明方法
邵恽益


摘 要:为了使中学生能高效解答勾股定理的题目,教师可以通过赵爽弦图证明、等面积、欧几里得证明和反证法等证明方法,使中学生更好地理解和掌握勾股定理的概念与本质。在日常的教学中,教师不断帮助学生理解勾股定理的证明,可以使学生更快和更熟练地运用勾股定理解决实际问题。
关键词:勾股定理;数学教学;证明方法
勾股定理是解直角三角形重要的定理与依据,它揭示的是直角三角形三边的数量关系,也是中考数学中必考的知识点。与此同时,在高中以及大学的数学学习中都会出现勾股定理,可以说勾股定理贯穿了学生的整个数学学习过程。除此之外,勾股定理还充分体现了数形结合的思想。勾股定理的证明能在一定程度上反映学生的创造思维和发散性思维的能力。本研究通过典型例子,综述中学阶段勾股定理的几种重要证明方法,以期帮助学生更深入地理解和掌握勾股定理的证明及运用。
一、赵爽弦图证明
这个证明方法是三国时期吴国的数学家赵爽提出的。赵爽创制了一幅“勾股圆方图”,利用形数结合得到方法,给出了勾股定理的详细证明。他用几何图形的截、割、拼、补来证明,既具有严密性,又具有直观性,过程如下:
五、拼图法证明
为了培养学生的动手能力,发挥学生的主观能动性以及体现学生的主体性,在日常教学中教师还可以引导学生通过使用七巧板或者三角形剪纸,自己动手拼图来证明勾股定理。用拼图法证明勾股定理的关键是抓住图形面积间的关系,与上文阐述的等面积法有异曲同工之处,即用不同的面积形式表示同一个图形的面积。
例题1. (解析题)如图5,是用硬纸板做成的两个完全一样的直角三角形,两直角边的长分别为a和b,斜边长为c,图6是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明勾股定理的图形。
问题1:画出拼成的这个图形的示意图,写出它是什么图形?
问题2:用这个图形证明勾股定理。
问题3:假设图5中的直角三角形有若干个,你能运用图5中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图。
这个方法重点在于用拼图法证明勾股定理,关键是抓住图形面积间的关系,利用同一个图形面积的不同表示法,列等式证明。让学生自己动手实践,不仅可以培养学生的学习兴趣,还能加深其学习印象,有利于学生更直观地理解勾股定理。
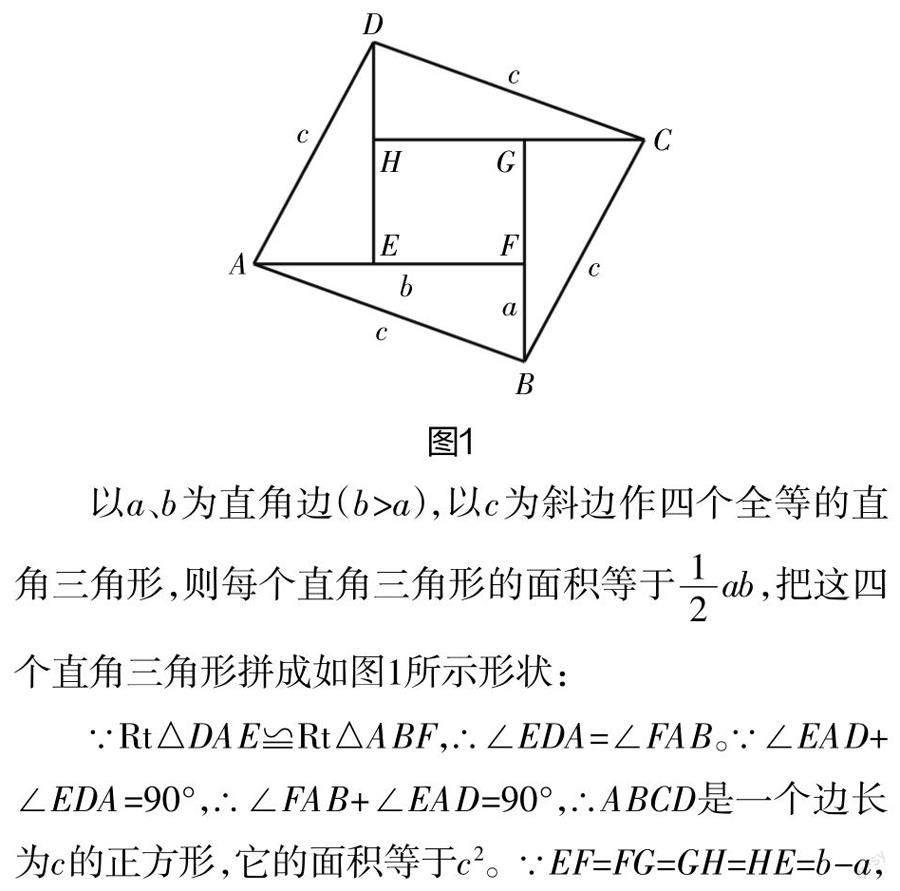
六、邹元治证明
以a、b为直角边,以c为斜边做四个全等的三角形,按图9所示相拼,使A、E、B三点共线,B、F、C三点共线,C、G、D三点共线。
七、综合应用现代技术教学
现代化技术的迅猛发展促进了教育教学领域的现代化发展,也为数学教学的信息化创造了必要的条件,从而改变了原有数学教学条件和方法。数学知识独特的抽象性、逻辑性,使学生凭空理解起来有一定的困难,但是通过信息技术能够改变传统教学中的缺点,使数学知识变得更加直观形象,并且更容易被学生接受,让学生能更加清晰地去观察并理解所学知识,从而充分巩固学生学习效果。
例如,教师在教学几何体知识时可以利用多媒体现代技术充当教学工具,通过图片、视频或者三维模拟图像等形式来将原本抽象的数学知识直观展示出来,创设良好的数学教学环境,从多角度多感官给学生展示,可以有效帮助学生更好地理解和学习,并且还能激发学生学习的兴趣,让学生充分感受到数学知识中的魅力。比如利用几何画板绘制毕达哥拉斯树,进行动画演示勾股定理的形成过程,如图10所示:
通过现代化教学工具的利用和多种证明方法的演示,不仅可以帮助学生更好的学习和掌握勾股定理,还能在学习过程中体会数学的乐趣和美妙,激发学生的学生兴趣,充分调动学生的积极性,使教学过程更加的丰富多彩。
八、结语
本研究主要总结了在勾股定理学习过程中一些常见的证明方法,教师在教学中加以运用,可以使学生在学习过程中更直观地理解勾股定理,提升学生的学习兴趣,发散学生的思维,锻炼逻辑思维能力,有效落实数学学科核心素养。
参考文献:
[1]李靖敏. 基于数学核心素养的课堂教学实践——“勾股定理”教学实践与反思[J]. 中国数学教育,2018(23):6-10.
[2]于秀坤. “赵爽弦图”走进中考[J]. 初中生学习指导,2021(05):32-33.
[3]韩诗贵. 勾股定理不同证明方法的价值与思考[J]. 中国数学教育,2021(Z3):62-64.
[4]房一丁,李霞. 关于勾股定理證明的一点思考[J]. 中学生数学,2022(16):32-34.
[5]田承恩,巩玉英. 新课改背景下勾股定理证明方法的问题探究[J]. 新课程教学:电子版,2020(08):56-57.
[6]石宇晴. 超级画板在中学勾股定理教学中的应用[A]∥新课程研究杂志社. 《新课改教育理论探究》第三辑[C]. 鲁东大学数学与统计科学学院,2020:82-83.
[7]董国玉,卢静. 赵爽与《周髀算经注》[J]. 兰台世界,2014(14):128-129.
[8]尹蕾. “一图多变”巧解题——从《几何原本》中勾股定理的证明说起[J]. 数学教学通讯,2016(17):62-64.
(责任编辑:淳 洁)

