一类行列式的差分法求解及推广

陈 滔，谭学忠

（1.华南师范大学 数学科学学院，广东 广州 510630；2.广东财经大学 统计与数学学院，广东 广州 510320）

行列式是《高等代数》中的重要内容之一.由于计算的技巧性强，没有统一的方法可循，因此也是学习中的一个难点.已有的许多文献对行列式的计算技巧进行的总结，方法包含化三角形法、加边法、递推法、数学归纳法、拆项法等，同时一些特殊类型的行列式也成为了研究的热点［1-6］.本文以一道考研行列式题目为例，给出差分法求解方法.

下面是北京大学的一道考研试题：

计算下面的行列式

提出一个更一般的问题，如何计算? 本文首先介绍差分的定义和符号，给出n阶差分的表达式，其次给出高阶等差数列的定义和若干性质，再次给出了行列式的一个重要性质及其计算公式，最后提出尚未解决的问题.

1 差分与高阶等差数列

本节主要给出差分和高阶等差数列的定义，同时给出两个与差分相关的引理，这两个引理在后面的证明中起着重要的作用，关于高阶等差数列的更多知识请参考文献［7-10］.

∆记为差分算子，ak记为某一数列的第k项则

一阶差分：Δak=ak+1-ak;

二阶差分：Δ2ak=Δak+1-Δak;

一般地，n阶差分：Δnak=Δn-1ak+1-Δn-1ak.

下面的引理给出了一个数列的第i项的n阶差分的计算公式.

引理1 设数列{an} 的第i项为ai，则

证明采用数学归纳法证明.

当n= 1 时，有a2-a1所以奇阶成立.当n= 2 时，有a3- 2a2+a1所以偶阶成立.

分别假设n= 2p- 1,n= 2p时，（p∈N+）奇偶阶都成立.现在考虑n= 2p+ 1 的情况.我们只考虑a1的情形，由假设有

证明对t作第二类数学归纳法：

当t= 1,n>1时,

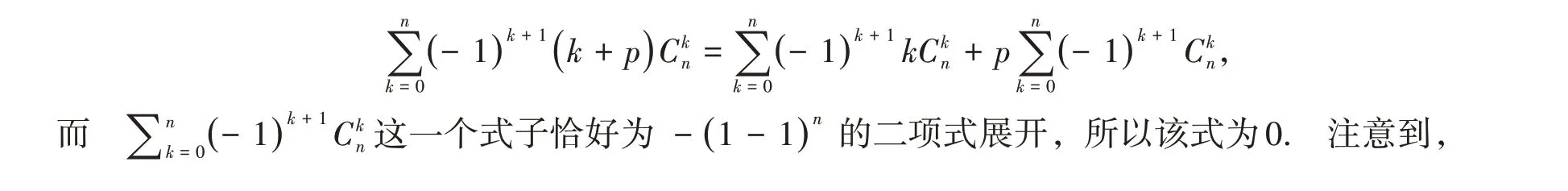
事实上，上述引理给出了一个特殊高阶等差数列的差分性质，将在后文中运用差分公式证明其为一个高阶等差数列，为此先介绍高阶等差数列的概念，并给出一些性质.

定义1 若{an} 第k阶差分为等差数列，则称{an} 为k阶等差数列.

定义2 在等差数列中，需要经过一次以上差分运算才能观察得到的高阶等差数列的公差称为隐藏公差，记作d.

性质1［9］数列{an} 任意项的差分为零当且仅当{an} 是常数列.

性质2［9］若某一数列是一个常数列，并且这一个常数列是通过一阶差分得到的，则原数列一定是等差数列.

通过上述性质，可以证明如下结论.

注：上述隐藏公差可以通过差分计算公式即引理1得出，其过程与引理2类似，故此处不再给出.

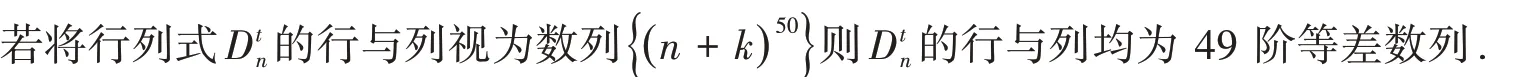
2 主要结论

对行做与列一致的初等变换，容易发现，此时仍是对元素进行差分运算，次数为r- 1 次.经过初等变换行列式可化为

证明由定理2容易证明.

注：回到开头的考研题目，n= 100,t= 50,n-t>2, 由定理3知，

3 未解决的问题

本文虽然给出了这一类行列式的两种情况，但是仍然还有一类情况没有给出，即n≤t这一类，目前仍然没有结论，我们将在后续文章中继续研究.