基于索筋剪叉式结构的展开式桥梁静力性能试验研究

孟磊，朱鸿涛，叶利宾，白文飞，张军，杨硕，王浩鹏

（1.北京市地铁运营有限公司技术创新研究院分公司，北京 100022；2.北京市地铁运营有限公司，北京 100044）

1 桥梁结构描述

图1 为本研究提出的可展开桥梁模型示意图。该桥梁采用甲板结构，上部为模块化甲板系统，下部承重结构采用钢索加固结构[1]。桥面系统由桥面和下纵梁组成。安装时，将纵梁端部与子结构节点处的卡扣连接，从而形成整个可展开桥系统。

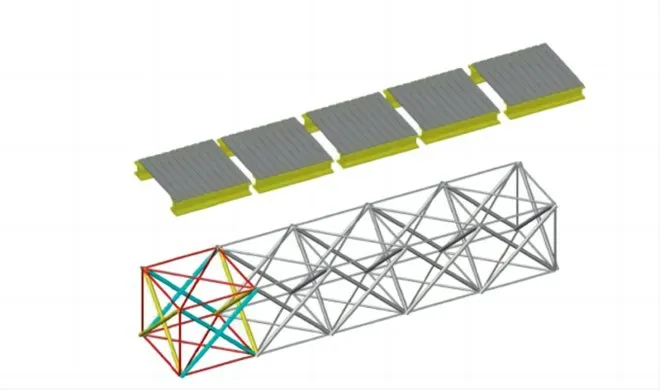
图1 可展开桥梁模型

桥梁下部承重结构采用模块化设计的钢索加固剪叉式结构，采用两根钢索将无钢索剪叉单元的上下节点（图2）连接起来，形成一个平面单元。单元内的钢索不影响剪叉结构的伸缩，可精确控制收缩角度。通过可展开控制器下，将剪式结构展开到设计角时，得到了结构的预期展开形状，同时完成了预张力的应用。这四个平面单元可以连接成一个三维单元[2-4]，即一个模块（图2）。模块与平面单元类似，可以自由伸缩，不受钢丝绳的影响。当模块被收紧时，其可以紧密收缩成束状，储存率高。为了防止平面单元之间的相对剪切变形，在模块的上下表面增加了两条交叉钢索，形成几何不变系统。各模块沿钢索方向重叠，形成桥下部钢索加固剪叉结构的承载结构，如图1所示。

图2 桥梁结构

2 试验方法

模型中剪叉结构采用建筑工程常用的Q345B 钢，规格为30mm×3mm 钢管，弹性模量为2.06×105MPa。每个钢材的长度为730mm。在钢材的两端和中间设置直径为10mm 的连接孔，两端孔直径中心之间的距离为707mm。

测试模型由三个三维元素组成，去掉重叠部分的平面元素。收缩后三个方向的三维单元尺寸均为0.5m。组合试验模型的长、宽、高分别为1.5m、0.5m、0.5m，如图3 所示。各单元剪件夹角约为45°。所有构件的长度相等，连接剪刀结构的所有钢索长度在纵向、横向和垂直方向上都相等。本试验主要考察了钢索及预紧力对构件刚度、承载力、轴向力和弯矩的影响[5]。因此，一个平面结构沿长度方向可以达到试验的目的。相反的结构和剪式单元在宽度方向上只起支撑作用。试验过程中，对平面结构和宽向单元的钢索全部释放。结果表明，当被测结构发生位移时，可以避免抑制效应[6]。由于两个平面结构在长度方向上不会发生相对运动，因此本试验不设置交叉钢索，以防止相对运动。

图3 测试模型

在1 号杆的C 位置对称布置2 个应变片，测量该点1 号杆表面因弯矩引起的表面应变（以下简称弯曲应变）。在杆1 的A、L 位置对称布置两个应变片，测量在这两点处杆1 表面轴向力引起的应变（以下简称轴向应变）。在杆2 的D 位置对称布置两个应变片，测量杆2 在该点处的弯曲应变，在杆2的A和F位置对称布置两个应变片，测量杆2 在该点处的轴向应变。在模型钢丝绳各截面的预设钢筋上设置应变片，以控制施加在钢丝绳上的预张力。在L 和E 位置设置两个位移计，测量模型在加载过程中的垂直位移。

3 结果与讨论

根据上述试验方案，得到了两结构节点位移与荷载的关系，以及测点表面应变与荷载的关系。具体测试结果分析如下。

3.1 索加固剪式结构静力性能分析

在钢索加固结构静力试验中，对该结构施加了四种不同的预应力。预紧力值由钢索力测量装置的应变片控制。应变控制值及相应张力如表1 所示。利用收集到的数据分析了预紧对结构刚度、内力和应力分布的影响[7]，得出以下结论。当钢索在服役时，钢索的预紧值对刚度基本没有影响。如果钢索停止使用，其刚度将显著降低。预紧力值随荷载变化对结构内力影响较小，截面内应力分布较为均匀。测试结果的详细分析如下。

表1 应变控制值及张力

3.1.1 钢索预紧力对刚度的影响

节点L 和节点E 的荷载-位移曲线如图4 所示。荷载-位移曲线的斜率反映了结构的刚度。如图4 所示，每条曲线大致可以划分为两个明显的部分。曲线的下半部分描述了上钢索和下钢索的工作状态，曲线的上半部分描述了下钢索的工作状态[8]。首先，曲线下部的斜率近似相等。这说明，当上下钢索均在使用时，结构刚度不受预紧力值的影响。第二，曲线的上部近似于一条直线，斜率非常接近。这说明当上部钢索不使用时，结构刚度仍然不受预紧值的影响，但不使用钢索对刚度影响较大，且曲线的拐点表明此时上部钢索开始停止工作。

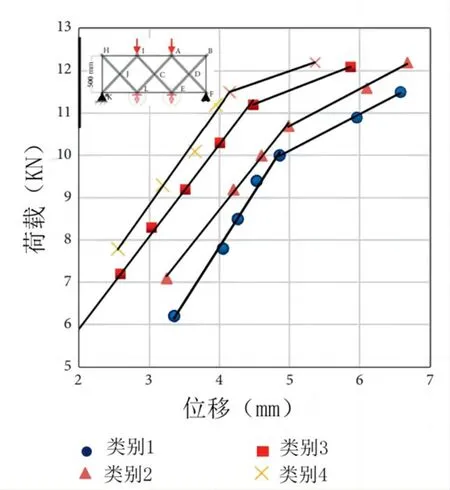
图4 钢索加固结构荷载-位移曲线

为清楚说明预紧力对结构内力的影响，以杆1 为例，得到不同预紧力下杆1的荷载-弯曲应变曲线和荷载-轴向应变曲线，如图5 所示。图中纵轴为外载荷，横轴为弯曲应变或轴向应变。

图5 钢索加固结构中杆1的荷载-内力应变曲线

虽然图5（a）中各曲线位置不同，但整体曲线形状与上述荷载-位移曲线基本一致。每条曲线可分为两个不同的段，分别对应上、下钢索的工作状态和单根下钢索的工作状态。曲线下部的斜率大致相同。结果表明，当上下钢索均在使用时，构件弯矩随荷载的变化规律几乎不受预紧值的影响。曲线上部的斜率也接近，说明当上部钢索不使用时，构件弯矩随荷载的变化规律仍然不受预紧值的影响。但可以发现，在上部钢索退出使用后，弯矩迅速增加[9]。图5（b）为预紧力对轴向力的影响。这些曲线呈直线上升，斜率相同，说明预紧力的大小对轴向力的变化没有影响，与钢索是否在役无关。

3.1.2 钢索预紧对应力分布的影响

构件所受内力的大小和类型直接决定了截面的设计。为研究钢索加固结构中构件的应力，比较了轴心处（C 位置）的弯曲应变和杆1 的轴向应变。图6 为杆1 的弯曲应变与轴向应变随荷载变化的比值曲线。横轴表示弯曲应变与轴向应变的比值，纵轴表示外部载荷。如图6 所示，比值在1 和2 之间，说明弯曲应变大于轴向应变。在该结构的设计中，弯矩的影响是不可忽视的。弯曲应变与轴向应变之比曲线可分为两段，分别对应上下钢索的工作状态和下钢索的单一工作状态。在曲线下部，该比值随荷载的增大而减小，说明弯矩的增长速度小于轴力的增长速度[10]。在上部曲线中，当上部钢索不使用时，随着荷载的增加，该比值开始迅速增大，这也说明弯矩在加速。通过对曲线的比较，可以得出上、下钢索的联合工作是非常重要的。

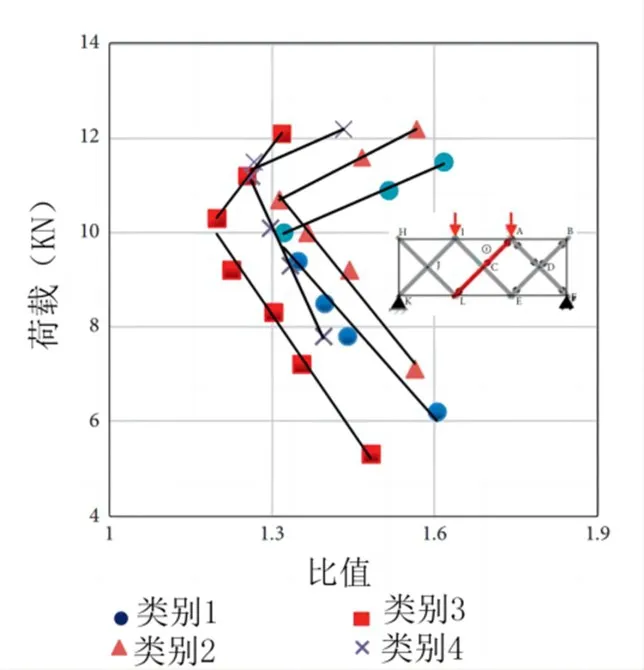
图6 钢索加固结构中构件1的弯曲应变与轴向应变之比曲线

3.2 无钢索剪式结构静力性能分析

锚索加固剪式结构静力试验结束后，将结构内所有钢索全部释放，并在剪式结构两端加设竖条，则得到稳定的对称结构。采用同一试验设备对结构进行三次加载，结构逐级加载不少于五层。同时采集了结构的位移、弯曲应变和轴向应变数据。试验结果表明，无钢索剪式结构刚度较小，模型在荷载作用下整体变形明显。构件支点处的弯曲应变很大，弯矩是无钢索剪式结构设计的重要参考指标。

3.2.1 无钢索剪式结构刚度

图7 为无钢索剪式结构的位移-荷载曲线。通过观察可以看出，位移-荷载关系总体上呈线性关系。当荷载较大时，两者之间的关系呈非线性趋势。当荷载达到9kN 时，结构位移已超过8mm，整体位移极大。试验表明，随着荷载的增加，中间单元向下移动，位移逐渐增大。当荷载较大时，两侧的单元开始向内旋转，并带动两端的垂杆向内旋转明显。结构的大变形使结构表现出一定的非线性。以上数据和现象表明，无钢索剪式结构的刚度较小。

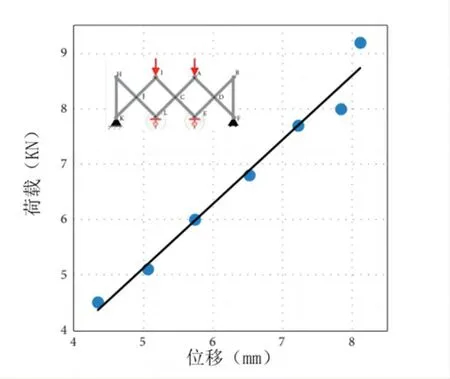
图7 无钢索结构的荷载-位移曲线

3.2.2 无钢索剪式结构的内力

图8 为杆1、杆2 和杆3 的载荷-弯曲和载荷-轴向应变曲线。在弹性范围内，荷载与应变的关系可以直接反映荷载与内力的关系。

图8 中的曲线呈明显的线性关系。然而，当荷载较大时，可以观察到偏离直线的个别点。结构在大荷载作用下的大变形，是由结构几何非线性造成的。如图8（a）所示，杆1 和杆3 的弯曲应变较大。在相同荷载下，杆1和杆3的弯曲应变是图8（b）中轴向应变的数倍，说明无索剪式结构部分构件的弯矩很大，不利于结构的承载能力。

图8 钢索加固构件1的荷载应变曲线

4 结论

本文提出了一种基于钢索加固剪形结构的三维可展开桥。除快速收缩外，还采用钢索加固剪式结构，以提高刚度和承载力。对有索加固和无索剪索结构进行了静力加载对比试验，得到以下结论。

①无钢索剪式结构刚度较小，导致结构位移大，构件截面弯矩大，应力分布不均匀。

②钢索加固剪形结构的刚度得到明显提高，构件的弯矩明显减小，应力分布更加均匀。因此，钢索加固剪式结构的承载能力大大提高。

③静载对比试验表明，钢索的加入显著提高了剪式结构的刚度，大大降低了内力，使构件截面内的应力分布更加均匀，从而提高了剪式结构的承载能力。