索强化剪式铰机构力学性能研究

俞 锋，许 贤，罗尧治

(浙江大学空间结构研究中心，浙江，杭州 310058)

剪式铰机构最早由西班牙建筑师Pinero[1]提出，组成剪式铰机构的剪式铰单元由两根杆件通过中部的转动副连接而成。剪式铰机构具有一个内部转动自由度，其形态改变易于控制，为可展结构的一个重要分支，常被用于移动帐篷、卫星天线、血管支撑架等小微型结构中。此类结构重点关注机构的展开形状和可动性，对机构的承载能力要求不高。现有文献对剪式铰机构的研究主要集中在几何构造和运动特性上。文献[2 - 3]分别给出了平面开环型剪式铰机构和空间网格剪式铰机构的设计方法。文献[4 - 5]论述了平面闭环型剪式铰机构的可动性。文献[6 - 7]研究了平面闭环型剪式铰机构的运动轨迹和运动奇异性。用平板代替平面闭环型剪式铰机构中的组成杆件可得到一类板式可展结构，文献[8 - 10]给出了板面设计方法使设计得到的板式可展结构在开合过程中满足几何相容性。

将剪式铰机构作为建筑结构主要承重构件的工程应用较少，相应剪式铰机构的力学性能研究也不多。文献[11]利用剪式铰单元的运动特性将剪式铰机构应用于预应力索拱开合结构中。文献[12]在几何线性假定下推导了直线排列剪式铰柱的抗压和抗弯刚度。采用该抗压和抗弯刚度，文献[13]将剪式铰柱等效成由弯曲刚度无限大的杆和杆间弹簧连接而成的分段柱，并给出了分段柱抗压屈曲承载力的计算方法。采用类似的等效方法，文献[14]研究了考虑自重的剪式铰柱的抗压屈曲承载力。图1 为剪式铰柱受压变形及受力分析图，随组成剪式铰单元数量的增加，剪式铰柱的受力变形存在较强几何非线性(图1(b))：一方面，竖向力向下传递过程中，下部单元需为相连的上部单元提供水平约束力，且该水平约束力会不断累加(图1(a))，致使下部杆件弯曲变形变大；另一方面，下部杆件的弯曲变形会进一步加剧上部单元的转动变形。

图 1 剪式铰柱受压变形分析Fig. 1 Compression deformation analysis of scissor column

文献[15]对剪式铰柱的受压变形进行了几何非线性分析，结果表明：柱的轴向变形主要来自剪式铰单元的内部转动，并且提出可以通过增加横杆的方式减小柱轴向变形(图1(c))。可见剪式铰单元的内部转动特性极大消减了成形后的结构刚度，并会在结构内部增加垂直力传播路径上的内力，且该增加内力会向支座附近的杆件累积。增加横杆约束可提高柱的轴向刚度，但会破坏剪式铰机构的可展性。

实际应用中，常在相邻剪式铰单元之间设置伸缩杆来强化剪式铰机构。如在剪式铰单元构成的升降机中，通过调整伸缩杆的长度来控制剪式铰机构的运动，并利用伸缩杆的约束来提高成形后的剪式铰机构的承载能力。此强化方法，不仅需要多个伸缩杆，且每个伸缩杆伸缩量的同步性需要额外的控制设备来保证。

本文采用索来强化剪式铰机构，利用索只受拉不受压的特性，在不影响机构运动的基础上，通过连续索提高展开成形后剪式铰机构的刚度和承载能力。文中首先介绍了索强化的剪式铰单元模型，并对索强化剪式铰单元的拉压刚度进行理论推导，阐明了索在提高剪式铰单元轴向刚度中所起的作用；然后在有限质点法计算框架下给出了连续索和剪式铰单元的计算方法以形成通用的索强化剪式铰单元受力分析方法，并通过数值算例验证了计算方法的准确性和合理性；最后对索强化剪式铰单元组成的半圆拱进行加载和连续索断裂分析，以探明连续索对剪式铰机构刚度和承载力的影响。

1 索强化的剪式铰单元

1.1 索强化剪式铰单元模型

根据组成杆件形状的不同，剪式铰单元可分为直杆剪式铰单元和折杆剪式铰单元(图2)。根据杆端连线夹角β(图2)的变化情况，直杆剪式铰单元可细分为相交和平行(β=0)两类；折杆剪式铰单元可细分为可变角和不变角(β 恒定不变)两类。现有剪式铰机构的构造均基于这几类基础剪式铰单元。

将剪式铰单元组成杆件的四个端点用索进行连接，可得到一个自平衡体系(图3(a))，相应的剪式铰单元将失去内部转动自由度。四条连接索根据其在剪式铰单元转动过程中的长度变化情况分成两组，变化趋势相同的归为一组。若将其中的一组索通过沿剪式铰单元杆件方向布置的索进行连接并形成连续索，便可利用该连续索的缩放来控制剪式铰的开合以及预应力的施加。如图3(b)所示，CA和DB为分段索；CB和AD为压杆，通过转动副O连接；CDAB为连续索，连续索和压杆AD的两端采用滑轮连接以减小连续索滑移时的摩擦力。该单元最早被用于可展天线的设计中[16-18]，以提高展开后剪式铰天线的刚度。

图 3 索强化剪式铰单元Fig. 3 Cable-strengthened scissor unit

对于索强化的直杆剪式铰单元，连续索的拉力不会增加杆段的弯矩以及中部转动副的剪力。本文将主要对直杆剪式铰单元进行索强化分析。分析时假定材料处于弹性阶段，并忽略索杆在节点处的偏心、杆件的轴向变形以及连续索和杆端间的摩擦力。

1.2 索强化剪式铰单元力学性能分析

通过张拉连续索施加预应力，当连续索的预应力为f时，索强化剪式铰单元各构件的内力可通过力平衡求解得到：

式中：下标字母对应构件连接节点；fADc为连续索段AD的内力；fADb为连续索经过的杆件AD的内力。本节的力、长度、面积、弹性模量、抗弯刚度分别采用如下单位：N、m、m2、N/m2、Nm2。

以外力施加方向为索强化剪式铰单元的轴向，对施加完预应力的索强化剪式铰单元进行轴向受力分析(图4)。在轴向力的作用下，剪式铰单元内的杆件有发生相对转动的趋势，从而引起索长(索内力)的改变，以此来抵抗轴向力的作用。

图 4 索强化剪式铰单元轴向受力分析Fig. 4 Axial force analysis on cable-strengthened scissor unit

在微小转动条件下，展开角度α(图4)可认为保持不变。以单元中点O作为参考点，则单元在轴力作用方向上的长度变化量Δ和D节点在轴力作用方向上的变形δ1以及垂直轴力作用方向的变形δ2存在以下关系：

式中：Ec为索的弹性模量；Ac1为分段索截面积；Ac2为连续索截面积。L1和L2为分段索和连续索的索原长：

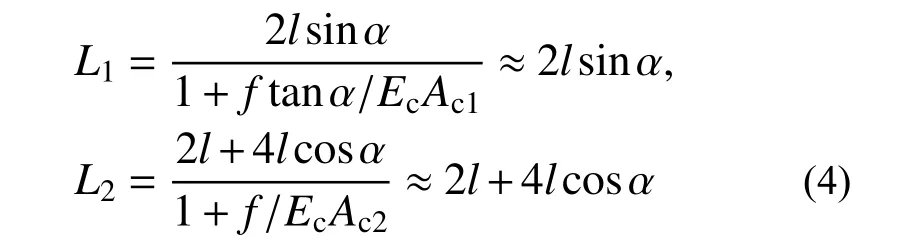
式中，l为剪式铰杆段长度。

对D节点进行受力平衡分析，当连续索索段CD和分段索BD均受拉时：

当连续索索段CD松弛退出工作时，力平衡方程变为：

上述分析可得，索强化后的剪式铰单元将具有轴向刚度，轴向刚度的大小与分段索和连续索的抗拉刚度、单元的展开角度以及预应力有关。式(7)、式(9)、式(11)表明：施加预应力后索强化剪式铰单元的轴向刚度分三个阶段：当拉压力较小时，分段索和连续索共同抵抗轴向力作用，此时单元的轴向刚度最大；随轴向拉力或压力的增加，连续索或分段索将退出工作，单元的轴向刚度随之退化。单元三个阶段的轴向刚度值和预应力大小无关，但预应力的大小决定了单元轴向刚度的退化节点。当无预应力作用时，单元轴向刚度将只存在两个阶段，单元的受拉刚度和受压刚度分别由分段索和连续索提供。

索强化剪式铰单元在弯矩作用下的弯曲变形如图5 所示。弯矩通过在A、C节点施加拉力，B、D节点施加压力模拟，施加弯矩M=Plcosα。以单元中点作为参考点，B、D节点和A、C节点在力作用方向变形δ11、δ21和垂直力作用方向变形δ12、δ22存在以下关系：

图 5 索强化剪式铰单元弯曲受力分析Fig. 5 Bending force analysis on cable-strengthened scissor unit

索强化剪式铰单元的等效抗弯刚度(EI)e可表示为：

可见在分段索BD退出工作前，索强化剪式铰单元的抗弯刚度和杆段的抗弯刚度、分段索的抗拉刚度以及展开角度相关，和连续索的抗拉刚度及预应力的大小无关。但预应力大小关系到分段索何时退出工作。

通过对一个规则索强化剪式铰单元受力性能的理论分析，得到了此类单元的各组成构件在抵抗外荷载时所起的作用，揭示了此类单元受力的一般规律。但对几何条件更为一般的索强化剪式铰单元，构件内力无法显式表达，且索强化剪式铰单元在外力作用下具有较强的几何非线性，需要采用数值计算方法来分析。

2 基于有限质点法的索强化剪式铰单元受力分析方法

索强化剪式铰单元的几何非线性主要来自两部分：连续索在接触点处的滑移；剪式铰两杆间的相对转动。本文采用有限质点法对索强化剪式铰单元的力学性能进行数值分析。有限质点法是基于点值描述和向量力学的结构行为分析方法，它采用质点对结构进行空间上的离散，以向量力学运动定律作为质点的运动准则，通过质点的位置参数求解结构的几何变形和内力[19-21]。

采用质点对结构进行离散时，使用的质点数量越多，结构的形态描述越接近实际情况，但计算量会随之增加。当重点关注杆件轴向变形时，可根据结构的拓扑关系进行离散，将质点设置在拓扑节点上。

质点的平动、转动满足牛顿运动定律：

为避免隐式解法带来的复杂迭代，有限质点法采用显式中央差分法求解质点运动方程：

虚拟阻尼系数的取值将影响质点到达静力平衡的所需时间，一般最优的虚拟阻尼系数可以通过结构的临界阻尼值计算得到。

2.1 连续索单元滑移分析

连续索滑移分析的关键是求解连续索在接触点处的滑移问题，也即索原长在接触点两侧的调整量[23-24]。不考虑接触点摩擦时，连续索各索段的内力相等，每个时间步计算结束时的各索段原长可按当前时间步各索段长度进行等比例分配。连续索各索段的内力增量 Δf可通过连续索的总长度改变量 Δl求解：

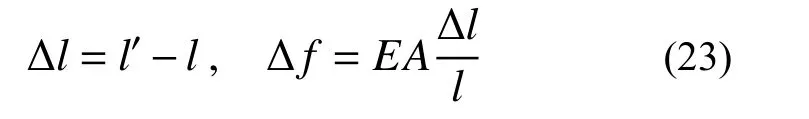
式中：l′为根据当前计算步质点坐标计算得到的连续索长度；l为连续索原长；A为连续索截面积；E为连续索弹性模量。

根据连续索内力增量更新连续索各索段内力，并将索段内力作用至接触点上，力作用方向由各索段的方向向量确定。当连续索松弛退出工作时，连续索对连接质点以及经过的接触点均无力的作用。

2.2 剪式铰单元转动分析

剪式铰单元模拟的关键是使两杆在转动副处的平面内转动位移相互独立，并使面外的转动位移及空间平动位移耦合。建立剪式铰单元计算模型时，可在转动副处设置两个质点分别连接剪式铰单元的两根杆件。文献[25]采用质点合力再分配法来处理平面剪式铰单元中部质点位移耦合问题。在二维平面内，质点不受面外力矩的作用，因此该方法未对中部质点的合力矩分配进行处理。

图 6 剪式铰单元局部坐标系Fig. 6 Local coordinate system of scissor unit

2.3 索强化剪式铰单元受力行为分析

图7 为基于有限质点法的索强化剪式铰单元计算模型。剪式铰杆件采用实心矩形钢杆，钢杆截面宽12.8 mm，高116.5 mm，弹性模量E=206 GPa，各杆段长l=1 m；连续索和分段索均采用10 mm直径钢丝绳，弹性模量E=170 GPa；展开角度α=45°；节点A和节点B分别采用固定铰支座和水平滑动铰支座。预应力施加完成后，杆BC、杆AD内力分别为-39 kN、-66.575 kN，连续索和分段索内力为27.575 kN。

图 7 基于有限质点法的索强化剪式铰单元计算模型Fig. 7 Calculation model of cable-strengthened scissor unit based on finite particle method

如图7(b)所示，离散成有限质点法计算模型时，杆BC和杆AD分别采用质点P2、P6、P4和P1、P3、P5描述，并使质点P3和P6的平动位移耦合；分段索AC和BD分别采用质点P1、P4和P2、P5描述；连续索BADC采用质点P2、P7、P8、P9、P10、P4描述，并将质点P1和P5作为索段P7P8和P9P10的接触点。

有限质点法通过动力过程来求解静力问题，节点C和节点D外力采用阶梯增长方式加载。根据文献[26]的建议，为保证静力解的可靠性，加载时长不应小于5 倍的结构最小自振周期。节点外力时程如图8 所示，其中时间变量为虚拟值，仅用于加载计算。有限质点法计算时，取时间步长Δt=1×10-5s，虚拟阻尼系数μd=10。

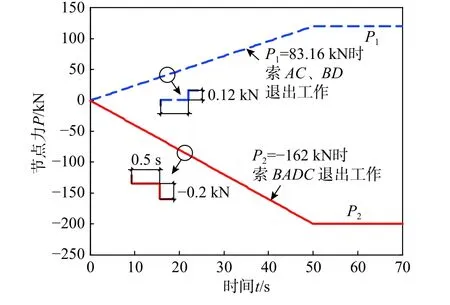
图 8 节点力-时程曲线Fig. 8 Node force-time curve

以外力时程P1为例求解加载过程中剪式铰单元的动能和应变能的比值关系。图9 为计算结果，可见和应变能相比，剪式铰单元的动能可忽略，说明该加载过程为准静态过程。

图 9 动能与应变能比值时程曲线Fig. 9 Time history curve of the ratio of kinetic energy to strain energy

外力时程P1、P2对应的D节点竖向位移时程曲线d1、d2如图10 所示。由图10 可见，当部分索松弛退出工作后，节点位移增速加快。

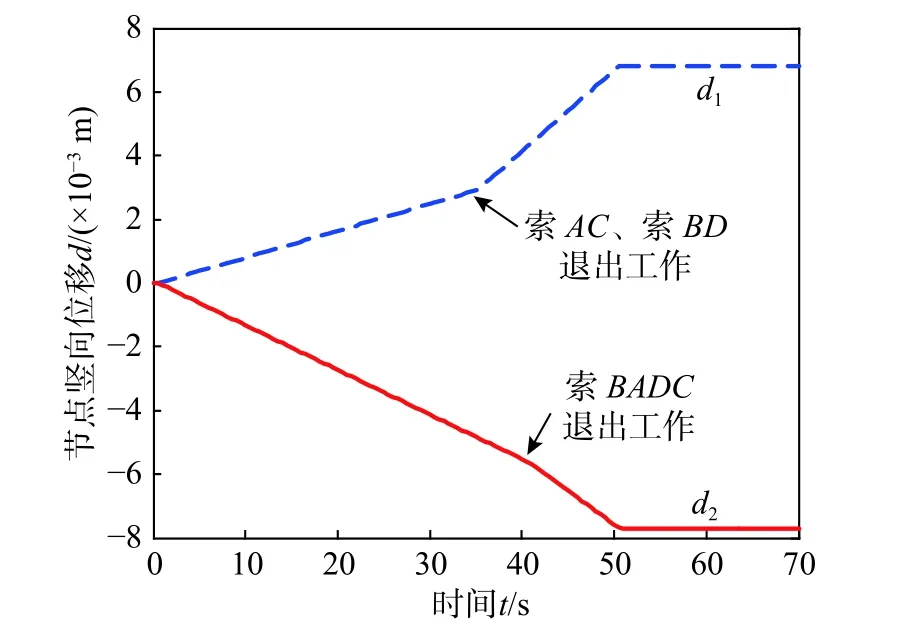
图 10 D 节点竖向位移时程曲线Fig. 10 Vertical displacement-time curve of node D

节点D的力-位移相关曲线如图11 所示。由图11 可得，有限质点法计算结果和本文推导公式计算结果基本吻合。力-位移曲线斜率反应了索强化剪式铰单元的轴向刚度，当部分索退出工作后，单元的轴向刚度也相应减小。解析解计算时未考虑单元受力后的几何非线性，当轴力较大时，解析解求得的单元刚度偏大。

为比较预应力大小对剪式铰单元轴向刚度的影响，取不同预应力状态下的剪式铰单元进行轴向加载分析，加载采用图8 所示的外力时程。计算得到节点D的力-位移相关曲线如图12 所示，图中F为不同预应力状态下的连续索和分段索的预应力值。

根据连续索和分段索是否退出工作，可将图12中的力-位移曲线划分成三个阶段(无预应力作用时不存在连续索和分段索均受拉的状态，所以只有两个阶段)，初始预应力越大索退出工作所需施加的外力越大。但不同预应力条件下，处于同一阶段的剪式铰单元的力-位移曲线斜率一致，表明其轴向刚度相同。当连续索和分段索均受拉时，剪式铰单元的轴向刚度最大，预应力可以延缓该轴向刚度的退化，但不能提高该轴向刚度值。

图 11 节点D 力-位移相关曲线Fig. 11 Force-displacement curve of node D

图 12 不同预应力条件下节点D 力-位移相关曲线Fig. 12 Force-displacement curve of node D under different prestress conditions

3 索强化剪式铰机构

将索强化剪式铰单元沿连续索方向进行叠加，并将连续索在单元之间进行连接，便可得到索强化的剪式铰机构。通过连续索可以控制剪式铰机构的开合，并施加全局预应力。本节将采用有限质点法对展开成形后的索强化剪式铰拱进行受力性能分析。

3.1 索强化剪式铰拱模型

图13 为展开成形后的索强化剪式铰半圆拱，内径10 m，厚度1 m，由12 个索强化剪式铰单元组成。剪式铰杆采用实心矩形钢杆，钢杆截面宽12.8 mm，高116.5 mm，弹性模量E=206 GPa；上、下弦分段索和连续索均采用10 mm 直径钢丝绳，弹性模量E=170 GPa。上、下弦分段索原长分别为2.8716 m、2.6105 m；连续索原长为58.9776 m；剪式铰单元中和上、下弦分段索相连的杆段长分别为1.5268 m、1.3880 m。

图 13 索强化剪式铰半圆拱Fig. 13 Cable-strengthened scissor-hinge semicircle arch

半圆拱通过支座Z1、Z2、Z3、Z4固定。施加预应力时仅设置支座Z2、Z3，其中支座Z2为固定铰支座，支座Z3为水平滑动铰支座。预应力施加完毕后将支座Z1、Z2、Z3、Z4均设为固定铰支座。

3.2 索强化剪式铰拱受力性能分析

拱预应力通过张拉连续索施加，施加过程中考虑结构自重作用。预应力施加完毕后，在图13所示节点处施加竖向节点外力P，P以0.01 s 增加0.1 kN 的阶梯增长方式从0 逐渐增加至10 kN。有限质点法计算时，取时间步长 Δt=1×10-5s，虚拟阻尼系数μd=10。

预应力施加完成后，连续索内力12 kN(应力153 MPa)，加载完成后连续索内力增加至15.8 kN。上、下弦分段索内力沿拱圆心角θ 的分布情况如图14 所示，cu、cd 分别表示上、下弦分段索，“加载前”表示预应力施加完成状态，“加载后”表示节点外力施加完成状态。施加预应力时，支座Z3可水平滑动，自重作用下拱截面上压下拉，跨中弯矩最大，此时下弦分段索内力大于上弦分段索内力。施加节点外力时，支座均固定，在节点外力作用下，拱跨中和支座附近的弯矩增量方向相反。节点外力施加完成后，跨中下弦分段索内力增大，上弦分段索内力减小直至松弛退出工作；靠近支座处的上下弦分段索内力的增减趋势正好相反。在预应力和节点外力作用下，剪式铰组成杆件以轴向受力为主。图15 为剪式铰杆段轴力沿拱圆心角θ 的分布情况，bc 为连续索经过杆段，b 为另一半杆段。受连续索的作用，bc 杆段所受的压力普遍比b 杆段的大。相同圆心角对应的bc 杆段和b 杆段的压力之和从拱顶向支座处增加，且整体随外荷载的增加而增大。

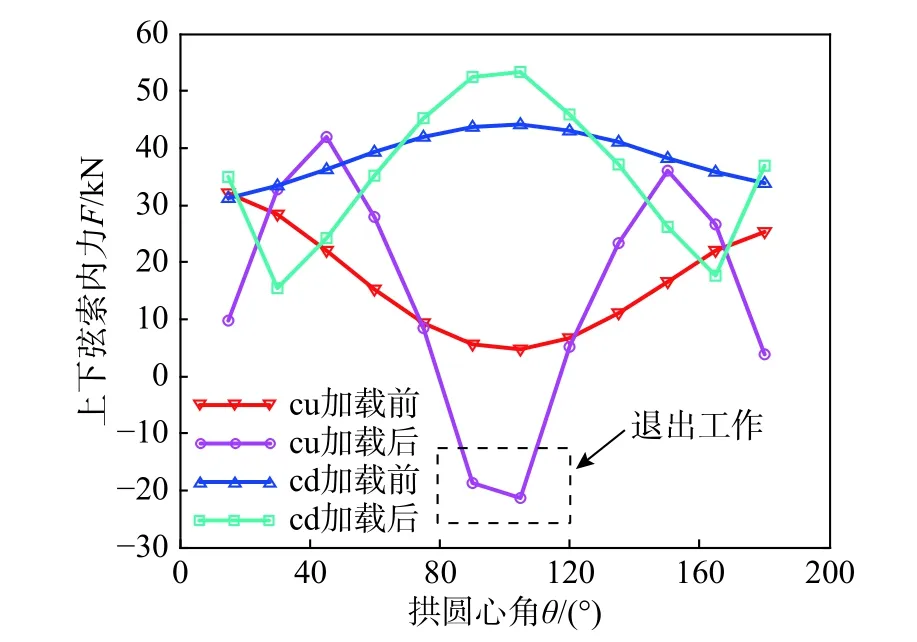
图 14 加载前后上下弦索内力分布Fig. 14 Internal force distribution of upper and lower cables before and after loading

图 15 加载前后剪式铰杆轴力分布Fig. 15 Axial force distribution of scissor-hinge before and after loading

待节点外荷载施加稳定后去除连续索来模拟连续索断裂的情况。从节点加载至连续索断裂过程中，拱跨中下弦节点(图13 节点20)的竖向位移时程如图16 所示。连续索断裂前节点20 在节点外力作用下仅发生0.05 m 的竖向位移；连续索断裂后，支座附近的剪式铰杆件受力变形加剧，跨中附近的剪式铰单元因缺少足够的约束而发生相对转动，带动整个拱向下运动，节点20 的竖向位移增加至3.176 m。可见连续索对索强化剪式铰机构的刚度至关重要。

随着拱的向下变形，拱上下弦分段索逐步退出工作，剪式铰杆段的内力也由受轴向力为主转变为受轴力和弯矩的共同作用。图17 和图18 为支座附近连续索经过的剪式铰杆段(图13 梁2)的轴力和弯矩时程。节点外力加载时，杆段所受轴力增加，但弯矩保持不变(为零)；连续索断裂后，杆段轴力由-89.3 kN 增加至-133.7 kN，弯矩由0 增加至100 kN·m。可见连续索对索强化剪式铰机构的内力传递及承载力有显著影响。

图 16 节点20 竖向位移时程Fig. 16 Vertical displacement-time curve of node 20

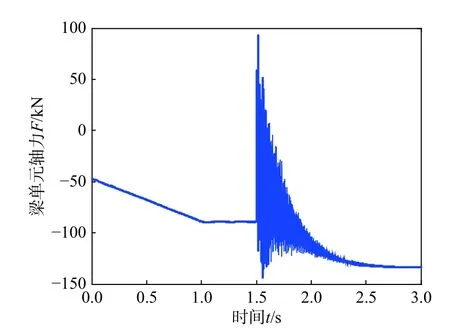
图 17 梁单元2 轴力时程Fig. 17 Axial force-time curve of beam element 2

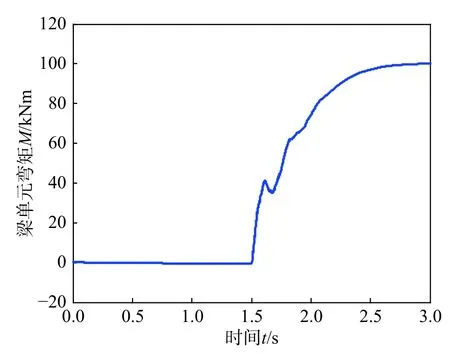
图 18 梁单元2 弯矩时程Fig. 18 Bending moment-time curve of beam element 2

4 结论

本文采用索对剪式铰机构进行强化，以提高剪式铰机构的刚度和承载能力。文中推导了规则索强化剪式铰单元的轴向刚度和抗弯刚度计算公式，给出了有限质点法计算框架下的索强化剪式铰单元的计算分析方法，并对一个典型的索强化剪式铰拱进行受力和断索行为分析。本文分析结果表明：

(1) 索强化剪式铰单元的轴向刚度主要由索的抗拉刚度提供，预应力可以延缓单元轴向刚度的退化，但不能提高单元轴向刚度峰值；单元抗弯刚度由剪式铰杆段的抗弯刚度和索的抗拉刚度共同提供。

(2) 索强化剪式铰机构可由索强化剪式铰单元组合得到，将单元间的连续索进行联通，通过连续索的缩放可控制机构开合及机构预应力的施加。

(3) 连续索对索强化剪式铰机构的刚度和承载力至关重要。连续索可有效减小剪式铰单元杆件的内部转动和弯曲变形。

(4) 连续索断裂后，支座附近的杆件弯矩和远离支座的机构变形将急剧增加，整体变形以剪式铰单元杆件的转动变形为主。