钢筋网高延性混凝土加固砖柱偏心受压性能试验及计算方法研究

邓明科，李 彤，范丽玮,2

(1. 西安建筑科技大学土木工程学院，陕西，西安 710055；2. 天津天华北方建筑设计有限公司，天津 300000)

在砌体结构加固工程中，针对砌体柱受压承载力不足的加固方法目前主要有钢筋混凝土面层加固法、钢筋网水泥砂浆面层加固法、外包型钢加固法和外加预应力撑杆加固法等。上述方法存在施工复杂、工期较长、增加结构自重、减小使用空间等缺点[1]。近年来，FRP(fiber reinforced polymer，纤维增强复合材料)已被广泛应用于既有砌体结构的加固维修[2-4]，其中，采用FRP 布包裹加固砖柱，通过约束砖柱的横向变形改善其受压性能，已取得了一些研究成果，但主要集中在轴心受压砖柱的研究方面[5-8]，对于偏心受压砖柱的研究鲜有报道。并且该方法也存在耐火性差、破坏突然、高温高湿环境下与砌体粘结性能差等缺点[9-10]。因此，探寻新技术和新材料以提高砌体柱的偏心受压性能具有重要意义。

高延性混凝土(highly ductile fiber reinforced concrete，HDC)是一种具有高强度、高韧性和高耐损伤能力以及受拉应变硬化的新型结构材料[11-13]。笔者研究团队将其用于钢筋混凝土柱[14]、砖砌体墙[15-17]的抗震加固，均取得了良好的加固效果。文献[18]采用HDC 面层包覆加固砖柱并进行了轴心受压试验研究，结果表明，HDC 面层约束了砖柱横向变形，大幅度提高了砖柱的承载力和变形能力。

为弥补传统加固法的不足，并进一步研究HDC 对砖砌体柱偏心受压性能的提高作用，本文提出采用钢筋网HDC 面层加固砖柱的方法，对27 个砖柱试件进行偏心受压性能试验，研究钢筋网HDC 面层加固后砖柱的破坏形态和受力性能，并提出了偏心受压砖柱正截面承载力计算方法。

1 试验概况

1.1 试件设计与制作

试验共设计了9 组砖柱，每组3 个试件，主要考虑了不同加固方式(两面或四面加固)和不同偏心距对砖柱受力性能的影响。《砌体结构设计规范》(GB 50003-2011)要求偏心距不应超过0.6y(y为截面形心到偏心方向截面边缘的距离)，以防止产生过大的受力裂缝，确保砌体构件在偏心受压时的安全性，但在实际工程中，屋面梁处容易出现轴力偏心距不满足规范要求的情况，故设计了4 个偏心距，分别为e=0、0.3y、0.6y和0.9y。按照《砌体基本力学性能试验方法标准》(GB/T 50129-2011)，采用尺寸为240 mm×115 mm×53 mm 的烧结普通砖砌筑。试件设计尺寸为240 mm×370 mm×720 mm，高厚比为3，钢筋采用HPB300 级。为保证纵向钢筋的锚固，在加固试件两端浇筑混凝土垫板。为方便试验加载，将偏心距较大(0.9y)的试件两端钢筋混凝土垫板外挑150 mm，试件设计参数见表1，详细尺寸及构造如图1 所示。

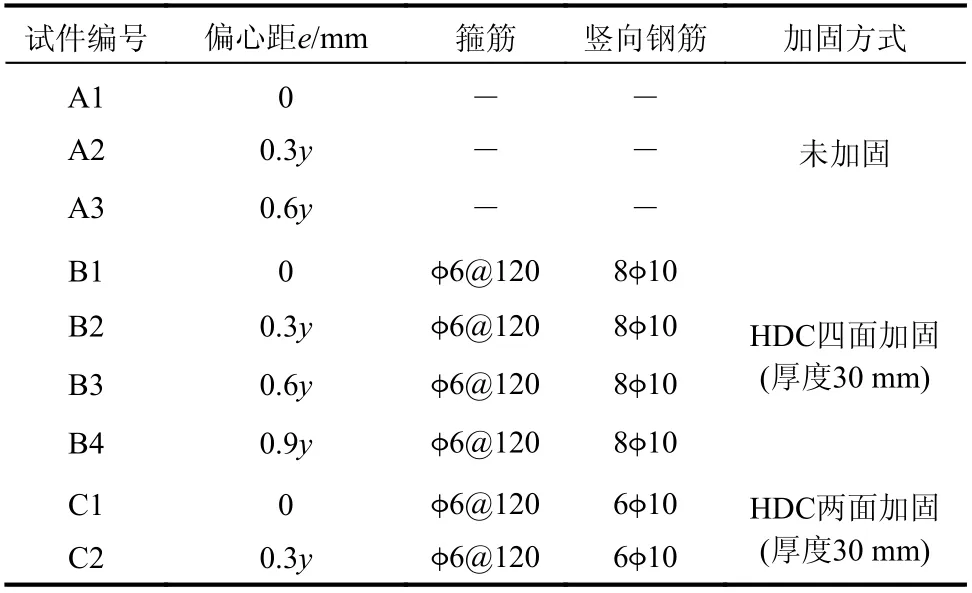
表 1 试件设计参数Table 1 Parameters of specimens

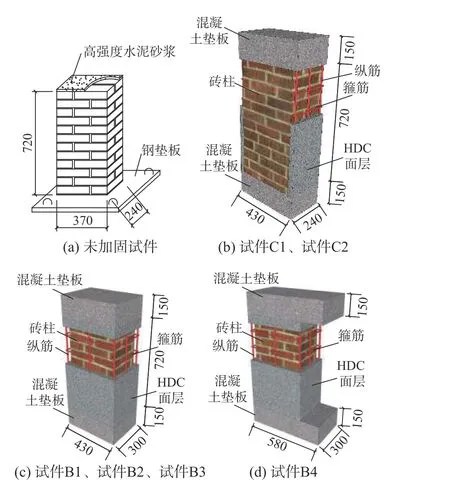
图 1 试件详图 /mmFig. 1 Details of specimens

1.2 材料力学性能

根据《砌墙砖试验方法》(GB/T 2542-2012)测得烧结普通砖的抗压强度平均值为7.87 MPa；采用边长为70.7 mm 的立方体试块，测得水泥砂浆的抗压强度平均值为3.01 MPa。

本试验采用的HDC 主要成分为水泥、粉煤灰、精细河砂、矿物掺合料、水、PVA 纤维和高效减水剂。PVA 纤维的体积掺量为2%，纤维各项性能指标见表2。HDC 的基本力学性能见表3。其中，fdcu为采用边长为70.7 mm 的立方体块测得的立方体抗压强度平均值；fdc为HDC 轴心抗压强度平均值，按文献[19]方法进行换算；fdt为采用350 mm×50 mm×15 mm 的哑铃型拉伸试件测得的HDC 轴心抗拉强度平均值。钢筋力学性能见表4。

1.3 试验装置与测试内容

本试验在5000 kN 液压伺服试验机上进行，对偏心受压试件，在试件上、下两端均安装单向转动的刀铰支座，通过调整刀铰位置实现不同的加载偏心距，加载现场如图2(a)所示。试验采用位移控制加载方式，加载速度为0.5 mm/min。主要测试内容包括砌体竖向变形值、HDC 面层变形值和钢筋应变值。测点布置与加载装置见图2(b)和图2(c)。

表 2 PVA 纤维各项性能指标Table 2 Performance indicators of PVA

表 3 HDC 的力学性能Table 3 Mechanical properties of HDC

表 4 钢筋的力学性能Table 4 Mechanical properties of steel

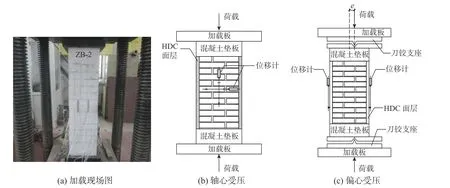
图 2 试验装置及测点布置Fig. 2 Test setup and layout of measurement points

2 试验结果及分析

2.1 试验现象

2.1.1 轴心受压(e=0)

1)试件A1

加载至极限荷载Pu的50%～60%时，试件表面出现第一条竖向裂缝；加载至(70%～80%)Pu时，竖向裂缝迅速向试件两端延伸，砌体表面有片状剥落现象；持续加载至极限荷载，竖向裂缝贯通，局部块体压碎脱落，试件承载力急剧下降，试件破坏。

2)试件B1、试件C1

试件B1 加载至(50%～65%)Pu时，HDC 面层沿角部出现竖向微裂缝并缓慢延伸；加载至80%Pu时，竖向裂缝明显变宽，窄面2/3 高度处HDC 面层外鼓，有剥离迹象；持续加载至极限荷载，窄面HDC 面层出现水平褶皱裂缝，局部剥离砌体，试件破坏。试件C1 破坏过程类似。

2.1.2 偏心受压(e=0.3y)

1)试件A2

加载至(50%～70%)Pu时，近轴力受压面出现第一条竖向裂缝；继续加载，远轴力侧出现水平裂缝，但延伸不明显，竖向裂缝则不断增多、延伸，并主要集中在刀铰下方；持续加载至极限荷载，近轴力侧的竖向裂缝贯通，角部砖块压碎脱落，试件破坏。

2)试件B2、试件C2

试件B2 加载至(45%～60%)Pu时，近轴力侧的HDC 面层中下部出现竖向裂缝并缓慢延伸；加载至80%Pu时，竖向裂缝明显加宽，局部面层外鼓；持续加载至极限荷载，近轴力侧的竖向裂缝贯通，部分面层与砌体剥离，试件破坏，而远轴力侧始终无明显现象。试件C2 破坏过程类似。

2.1.3 偏心受压(e=0.6y)

1)试件A3

加载至(25%～35%)Pu时，远轴力侧的窄面上出现第一条水平裂缝；随着荷载的继续增大，水平裂缝不断加宽，并出现新的水平裂缝；加载至70%Pu时，刀铰下方的两宽面出现竖向裂缝；持续加载至极限荷载，水平裂缝发展很宽，并延伸至两宽面的2/3 处，而竖向裂缝主要分布在近轴力侧的砖柱中上部，没有上下贯通，局部砖块压碎脱落，试件破坏。

2)试件B3

试件B3 破坏过程与试件B2 类似，不同点在于远轴力侧的受压面仅在加载后期出现水平受拉裂缝，且没有延伸、加宽，持续加载至极限荷载后，近轴力侧竖向裂缝贯通，试件破坏。

2.1.4 偏心受压(e=0.9y)

试件B4 加载至(45%～65%)Pu时，远轴力侧的中下部出现水平受拉裂缝，并不断延伸、加宽，且出现新的水平裂缝；加载至80%Pu时，近轴力侧受压面出现竖向裂缝；持续加载至极限荷载，水平裂缝发展较宽，竖向裂缝贯通，个别HDC 面层与砌体剥离，试件破坏。典型试件破坏形态如图3 所示。

2.2 破坏形态

根据3 组轴压试件和6 组偏压试件的试验现象和破坏过程可得：

1)试件A1、试件B1、试件C1 均发生轴心受压破坏。试件A1 破坏时，由于竖向裂缝贯通，砖柱被分割成若干个独立的细长小柱体，最终因小柱体失稳或压碎而破坏，呈明显脆性破坏特征；试件B1、试件C1 采用钢筋网HDC 面层加固，破坏时HDC 面层由于直接受压而产生水平褶皱裂缝，并且砖柱角部应力集中使HDC 面层沿竖向开裂，两种裂缝共同作用下HDC 面层局部剥离砌体，但未剥离面层仍具有较高承载力，荷载下降缓慢，最终因砌体局部压碎而破坏，试件保持了良好的整体性。

图 3 典型试件破坏图Fig. 3 Typical failure modes of test members

2)试件A2、试件B2、试件B3、试件C2 均发生小偏心受压破坏。未加固砖柱(试件A2)破坏时，近轴力侧砌体角部砖块压碎脱落，远轴力侧砌体出现少量水平受拉裂缝，达到极限荷载后，突然丧失承载力，呈明显脆性破坏特征；加固柱(试件B2、试件B3、试件C2)破坏时，近轴力侧面层竖向裂缝贯通，个别HDC 面层与砌体剥离，但未剥离面层仍能良好受力，而远轴力侧砌体无明显现象或仅出现少量水平拉裂缝，根据钢筋应变测试结果，远轴力侧钢筋无论受压或受拉均未达到屈服状态，具有小偏心受压破坏特征，但高延性混凝土受压时具有良好的抗压韧性，防止了试件的突然破坏。

3)试件A3 破坏时，远轴力侧的砌体形成较宽的主拉裂缝，近轴力侧砌体上部砖块压碎脱落，竖向裂缝没有上下贯通，可认为其属于大偏压破坏；试件B4 破坏时，远轴力侧的HDC 面层形成细密的水平裂缝，且分布均匀，受拉钢筋应变接近屈服，近轴力侧的窄面HDC 面层局部与砌体剥离，最终发生砌体压碎破坏，具有大偏心受压破坏特征。

2.3 荷载-位移曲线分析

以对比组试件的峰值荷载和峰值位移作为参考点，将各试件的荷载-位移曲线进行归一化处理，如图4 所示。从图4 中可以看出，未加固砖柱刚度小、变形能力差，几乎没有塑性变形，达到极限荷载后承载力迅速下降，呈明显脆性破坏特征。采用钢筋网HDC 面层加固后砖柱的初始刚度得到明显提高，尤其四面加固砖柱的提高幅度更大；接近极限荷载时，试件的荷载-位移曲线发生明显弯曲，曲线斜率逐渐变小，砖柱表现出明显的弹塑性变形特征；加载至极限荷载以后，荷载-位移曲线较为平缓，承载力下降缓慢。总体来看，钢筋网HDC 面层可大幅度提高砖柱的初始刚度和变形能力，改善砖柱的脆性破坏特征。

2.4 承载力分析

各组试件的试验结果列于表5，由表5 可以得出：

1)与未加固砖柱相比，采用钢筋网HDC 面层加固的砖柱开裂荷载提高43%～383%，极限荷载提高45%～265%，说明钢筋网HDC 面层能够良好受力，延缓了砖柱的开裂过程，限制了竖向裂缝的开展，大幅度提高了砖柱的受压承载力。

2)与试件C1 和试件C2 相比，试件B1 和试件B2 的开裂荷载分别提高93%和48%，极限荷载分别提高98%和76%，说明钢筋网HDC 四面加固可有效约束砖柱的横向变形，抑制砖柱竖向裂缝的开展，使得砖柱轴向承载力大幅度提高，其加固效果明显优于钢筋网HDC 两面加固。

图 4 荷载-位移归一化曲线Fig. 4 Normalized load-displacement curves

3)与轴心受压砖柱相比，偏心受压砖柱的开裂荷载、极限荷载均随着偏心距的增大而减小，对于未加固砖柱，其极限荷载分别降低40%和46%，采用钢筋网HDC 两面加固后，极限荷载降低15%，采用钢筋网HDC 四面加固的砖柱，其极限荷载分别降低24%、45%和52%，分析原因如下：初始偏心距在砖柱截面产生应变梯度，减小截面的受压面积，偏心距越大，远轴力侧的拉应力越大，越容易产生水平受拉裂缝，砖柱受压承载力降低更加明显。然而，对于钢筋网HDC 面层加固砖柱来说，由于HDC 受拉时具有多裂缝开展特性，且抗拉强度远高于砌体，因而在偏心荷载作用下，HDC 延缓了水平裂缝的开展，因此，偏心距相同时，加固试件的极限荷载降低幅度小于未加固砖柱，说明钢筋网HDC 面层在偏心荷载作用下仍具有良好的加固效果，可有效提高砖柱的偏压承载力。

2.5 纵筋、箍筋及HDC 面层应变分析

根据加固材料的应变测试结果绘制出纵筋、箍筋以及HDC 面层的荷载-应变关系曲线如图5所示。图5 中，正值表示拉应变，负值表示压应变。根据曲线可得：

1)轴心受压砖柱(试件B1、试件C1)达到极限荷载时，受压纵筋基本达到屈服状态，钢筋强度得到有效利用；HDC 面层由于核心砌体的膨胀，处于拉、压复合受力状态，并且破坏时存在剥离现象，导致HDC 的压应变值较小。

2)小偏心受压砖柱(试件B2、试件B3、试件C2)达到极限荷载时，近偏心侧的受压纵筋接近屈服，而远偏心侧的纵筋应变随偏心距增大逐渐从压应变转为拉应变，但均未达到屈服状态，说明随偏心距增大，截面受压区高度逐渐减小，试件承载力也逐渐降低。

3)试件B4 达到极限荷载时，远偏心侧纵筋受拉接近屈服，近偏心侧纵筋受压屈服，钢筋强度基本得到充分利用；近偏心侧HDC 面层直接受压而外鼓剥离，其应变较小，远偏心侧HDC 处于受拉状态，砖柱破坏时具有大偏心受压破坏特征。

4)所有试件的箍筋应变在加载前期增长较慢，接近峰值荷载时快速增大，表明箍筋在核心砌体产生明显的横向膨胀以后，发挥了较强的被动约束作用。

3 承载力实用计算方法研究及二次受力分析

3.1 基本假定

1)认为核心砌体达到极限压应变 εult时，砖柱破坏；

2)截面应变分布符合平截面假定；

3) HDC 与砌体之间粘结良好，不产生滑移；

4)不考虑砌体的抗拉作用。

3.2 材料本构模型

1)砖砌体受压本构模型

2) HDC 本构模型

HDC 受拉时具有应变硬化效应，取其应力-应变曲线的上升段为斜直线，下降段为水平直线，如图6(a)所示，其单轴拉伸应力-应变关系为：

HDC 受压应力-应变曲线采用双线性模型，如图6(b)所示，应力-应变关系为：

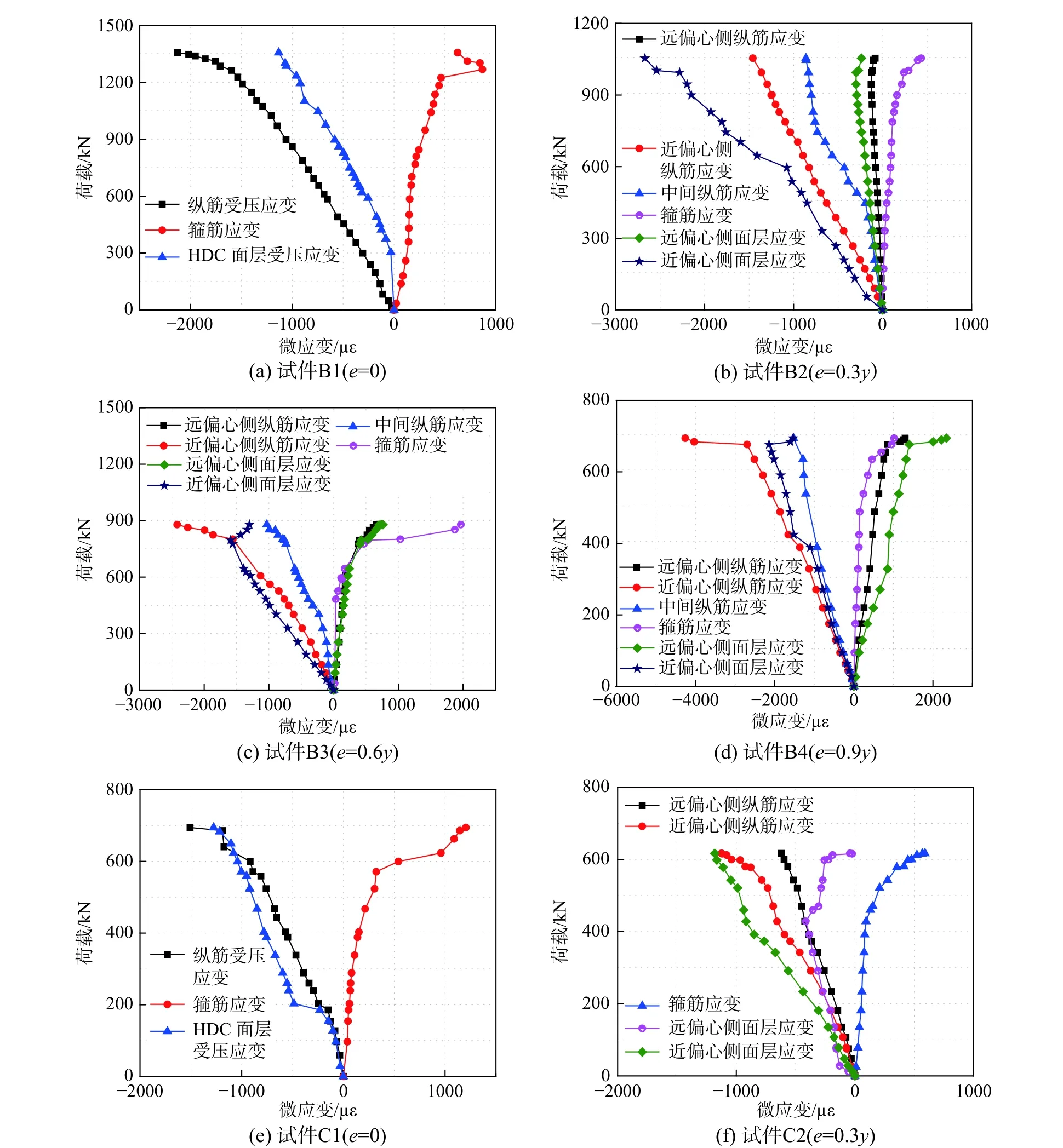
图 5 荷载-应变曲线Fig. 5 Load-strain curves

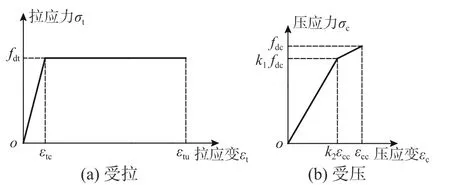
图 6 HDC 应力-应变曲线Fig. 6 Stress-strain curves of HDC

表 6 HDC 本构模型参数Table 6 Parameters of constitutive model of HDC

3)钢筋本构模型

本文所用钢筋具有明显屈服平台，故采用理想弹塑性模型。

4) HDC 材料强度利用系数

加固层厚度远远小于砖柱截面高度，因此，根据上述基本假定，当砖柱破坏时，加固层HDC的压应变近似可取为 εcd=εult=0.0031，此时，HDC 应变小于其材料峰值压应变，其材料强度并未得到充分发挥，因此提出HDC 的强度利用系数α0，由式(4)计算可得：

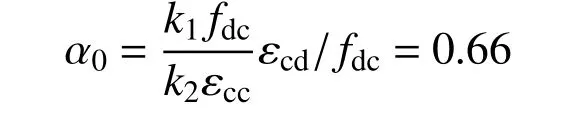
3.3 钢筋网HDC 面层加固砖柱偏压承载力计算

3.3.1 截面受压区的计算简化

以四面加固砖柱为例，计算简图如图7 所示。受压区分为C1、C2 和C3 三个区域，并规定在构件处于全截面受压状态时，计入截面中部两根纵筋的应力。设加固后截面宽度为b1，截面高度为h1，截面有效高度为h0，截面中和轴到受压砌体边缘的距离为x。

C1 区砌体的压应力呈曲线分布，为简化计算，参考文献[21]，采用等效矩形应力图形替换，在砌体受压边缘达到极限压应变 εult时，αm取0.8755， βm取0.7731。其中， αm为等效矩形应力图形的应力与砌体抗压强度平均值的比值，βm为等效矩形应力图形的高度与实际应力图形高度的比值。

C2 区HDC 厚度远远小于截面受压区高度，为使计算偏于安全，假定该区HDC 的应变均匀分布，并等于砌体极限压应变 εult，由此计算得该区HDC 压应力为 α0fdc。

HDC 的抗压强度远远高于砌体，因此，C3 区的HDC 应力不可忽略，根据其三角形的应力图形分布可得竖向力为 0.5α0fdcxt。

3.3.2 截面受拉区的计算简化

截面受拉区的计算简化可分为考虑HDC 的抗拉作用和不考虑HDC 的抗拉作用两种情况进行。考虑HDC 的抗拉作用时，仅考虑T1 区高延性混凝土的抗拉贡献，根据应变协调条件，以受拉钢筋的应变作为HDC 的拉应变，且认为该区应力均匀分布，如图7 所示。根据相似关系可得：

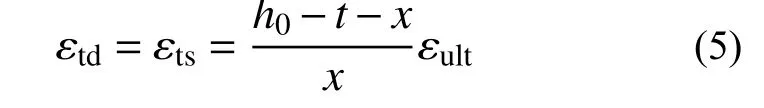
3.3.3 偏心受压柱的正截面承载力计算公式

根据上述简化方法，极限状态时各关系式如下：

式中：fm0为原构件砌体抗压强度； αs为受压纵筋强度利用系数，本试验取1.0；fy′为新增受压竖向钢筋的屈服强度；As为新增受拉区竖向钢筋截面面积；A′s为新增受压区竖向钢筋截面面积；Asm为新增截面中部竖向钢筋截面面积； σs、 σd分别为受拉区的竖向钢筋应力和HDC 应力，按材料的本构方程计算； σsm为截面中部两根钢筋应力，其应变按式(7)计算：

附加偏心距ea的计算参考《砌体结构加固设计规范》(GB 50702-2011)得：

式中， β为加固后试件高厚比。

不考虑HDC 的抗拉作用，或者忽略截面中部两根纵筋应力时，只需删除式(8)和式(9)中相应部分即可。

3.3.4 计算结果分析

根据上述公式所得的试件承载力计算结果列于表7，由表7 可见，试件的计算值与试验值吻合较好，相对误差均在15%以内。另外，根据计算结果可以看出，是否考虑HDC 的抗拉作用对计算结果影响不大。因此，为了便于砌体偏压柱的加固设计，可不考虑HDC 的抗拉作用。

表 7 试验值与计算值的比较Table 7 Comparison of test and calculation results

3.4 二次受力加固层应变滞后分析

在实际工程中，对竖向构件进行加固时很难做到完全卸载，加固层应变滞后于原结构，本节主要分析二次受力的应变滞后对加固柱承载力的影响，各项基本假定和材料本构关系如前所述。为了便于工程设计，定义砖柱的初始应力水平指标 β0为加固前砖柱所受轴向荷载与理论轴向荷载之比，计算如下：

式中， σ0为砖柱的初始竖向压应力。

砖柱在初始偏心荷载作用下，其截面应变分布如图8 所示。

图 8 砖柱截面应变分布Fig. 8 Strain distribution of masonry column

对砖柱采用钢筋网HDC 面层加固并加载至极限状态时，截面应变分布见图8。受压边缘钢筋和HDC 的实际应变为：

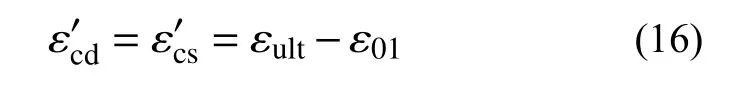
截面中部钢筋的实际应变为：

将上述分析计算的不同应力水平和偏心距下的HDC 抗压强度利用系数列于表8，表8 中其余强度利用系数取值可由线性插值法求解，并绘制α0随初始应力水平的变化曲线，见图9。

表 8 HDC 抗压强度利用系数Table 8 Compression strength reduction factor of HDC

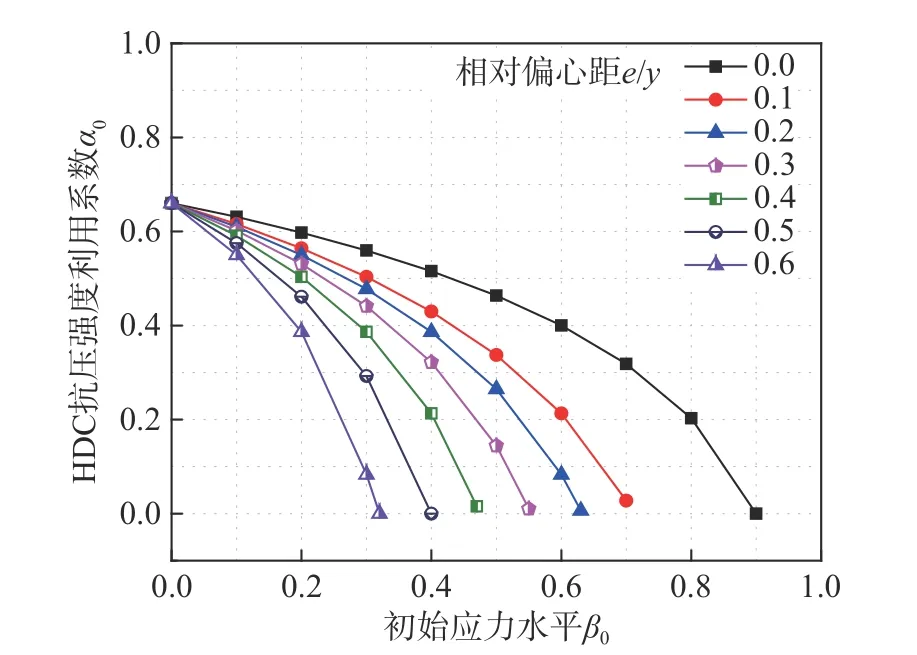
图 9 初始应力水平- α0 关系曲线Fig. 9 Initial stress level -α0 curves

由图9 可见，HDC 抗压强度利用系数随初始应力水平、初始偏心距的增大而减小，初始应力水平越高，利用系数降低速度越快。结合上述分析可见，考虑二次受力的影响时，钢筋网HDC 面层加固偏压砖柱的承载力计算公式仍可采用式(8)和式(9)，仅需用式(17)和式(18)代替式(5)和式(7)。

4 结论

通过27 个砖柱的受压试验研究和理论分析，研究了钢筋网高延性混凝土面层加固砖柱在偏心受压荷载作用下的受力性能，探讨了二次受力的应变滞后对加固柱承载力的影响，可得出以下结论：

(1)与未加固砖柱相比，采用钢筋网HDC 面层加固的砖柱开裂荷载提高43%～383%，极限荷载提高45%～265%，说明钢筋网HDC 面层与砌体具有良好的协调工作能力，限制了竖向裂缝的开展，可大幅度提高砖柱的偏心受压承载力。

(2)采用钢筋网HDC 面层加固的砖柱达到极限荷载以后，承载力下降缓慢，说明钢筋网HDC面层约束了砖柱的横向变形，可有效提高砖柱的变形能力，改善了砖柱的脆性破坏特征，发挥了HDC 高韧性的特点。

(3)与C 组试件相比，B 组试件的开裂荷载提高48%～93%，极限荷载提高76%～98%，说明钢筋网HDC 四面加固有效地约束了砖柱的横向变形，延缓了砖柱的开裂过程，大幅度提高了砖柱的受压承载力，其加固效果优于钢筋网HDC 两面加固。

(4)随偏心距增大，截面应变梯度增大，受压区高度减小，砖柱的承载力逐渐降低，但采用钢筋网HDC 面层加固后，由于HDC 抗拉强度较高，且具有受拉多裂缝开展特性，在偏心荷载作用下，HDC 延缓了水平裂缝的开展，因此，偏心距相同时，加固试件的极限荷载降低幅度小于未加固砖柱，说明初始偏心距并未削弱钢筋网HDC面层的加固效果。

(5)考虑HDC 的抗拉作用，并对加固层的应力进行计算简化，得到钢筋网HDC 面层加固偏压砖柱的承载力计算公式，与试验结果吻合较好。

(6)对砖柱受压加固的二次受力进行了分析，给出了不同初始偏心荷载作用下的HDC 抗压强度利用系数，可供加固设计参考使用。