“解几”背景,“平几”融合:从一道高考试题谈起

张 鹏

江苏省扬州市第一中学

平面解析几何综合问题,经常融入平面几何背景,是基于平面几何知识的进一步提升与拓展,成为高考数学命题中的一个重要场景与应用.在处理此类问题时,经常要合理借助平面几何的直观,把握平面解析几何的实质,进而综合分析与解决问题.同时,此类问题也很好地兼顾了高考数学试题的基础性、综合性、创新型和综合性,以及试题间的层次性,合理调控综合程度.

1 真题呈现

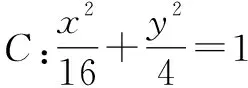
2 真题剖析

该题以椭圆为问题背景,结合点的对称、线段的长度关系以及矩形的确定,进而求解对应四边形的面积,巧妙地将平面几何与平面解析几何知识加以合理交汇与融合,合理串联起“数”与“形”的联系,数形结合,直观想象.

破解问题的关键是根据条件,通过确定平面四边形的形状,借助椭圆的定义、解直角三角形、坐标处理或焦半径公式等,破解思维多变,技巧方法多样.具体破解时,“数”与“形”相互转化、相互协作,可代数运算,可数形结合,更加直观形象地破解问题.

3 真题破解

上述高考真题解法如下.

解法1：椭圆定义法.

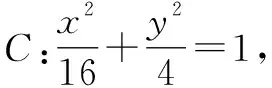
依题目条件可知,四边形PF1QF2为矩形.

设|PF1|=m,|PF2|=n,利用椭圆定义可得m+n=2a=8,则m2+2mn+n2=64.

又结合矩形的性质,可得m2+n2=|F1F2|2=4c2=4(a2-b2)=48,则mn=8.

故所求四边形PF1QF2的面积为|PF1||PF2|=mn=8.故填答案:8.

点评：圆锥曲线的定义及其应用,是解决圆锥曲线的综合应用问题中比较常用的基本知识点之一.本解题方法的关键就是抓住椭圆的定义来分析与应用,为解决其他应用问题奠定条件.这也是实现定义先行的根本策略.抓住定义,从定义视角入手,由此来构建相应的关系式,为问题的进一步分析与求解建立基础,也是综合应用问题的基石.

解法2：解直角三角形法.

依题目条件可知,四边形PF1QF2为矩形.

如图1所示,设∠PF1F2=α,则在Rt△F1PF2中,|PF1|=2ccosα,|PF2|=2csinα.

图1

点评：利用题目条件先判断四边形PF1QF2为矩形,在Rt△F1PF2中设出对应的角,结合已知斜边确定两直角边,通过解直角三角形,并结合椭圆的定义建立所涉角的三角关系式,利用矩形的面积公式以及三角关系式的恒等变形,进而得以求解四边形的面积.利用解直角三角形的思维解决问题,一直是初中平面几何中比较常见的思维方式,也是我们平时解决问题的常用技巧.

解法3：坐标法.

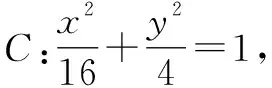
①

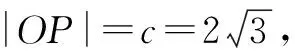
②

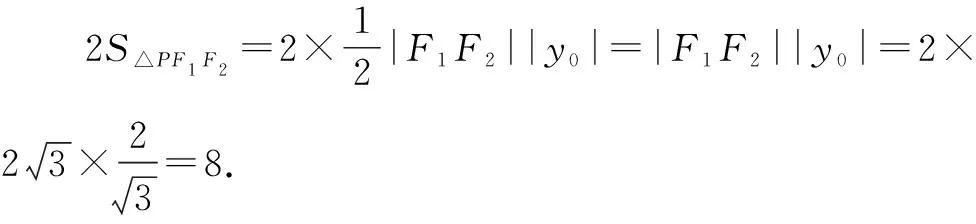
点评：设出点P的坐标,其满足椭圆方程,根据点P的位置关系确定其到坐标原点的距离,进而建立相应的关系式,通过两式对应的代数运算与化简,得到点P的纵坐标的绝对值,即对应三角形斜边上的高,进而利用图形的对称性求解四边形的面积.转化三角形对应的底边与高,可以求解任意形状的三角形的面积,具有一般性.

解法4：焦半径公式法.

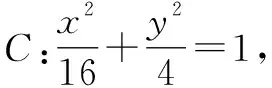
依题目条件可知,四边形PF1QF2为矩形.

设P(x0,y0),则有

③

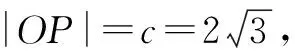
④

根据椭圆的焦半径公式,可得|PF1|=a+ex0,|PF2|=a-ex0.

故填答案:8.

点评：利用题目条件先判断四边形PF1QF2为矩形,设出点P的坐标,其满足椭圆方程,根据点P的位置关系确定其到坐标原点的距离,进而建立相应的关系式,通过两式对应的代数运算与化简,得到点P的横坐标的值;结合椭圆的焦半径公式,并利用矩形面积公式建立关系式,代入对应的数值即可求解对应的四边形面积.焦半径公式法是处理与圆锥曲线的焦半径有关的问题的一大常用技巧.

4 变式拓展

根据以上高考真题以及破解过程,可以将问题进行一般化处理,注意条件中线段关系式成立的前提,进而可以得到一般性的结论.

具体证明过程可以直接参照以上高考真题的破解过程,这里不再赘述.

保留问题的背景,改变问题的设问方式,可以用不同的方式来设置问题,而具体的求解结果保持不变.

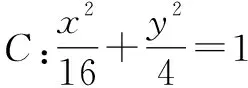
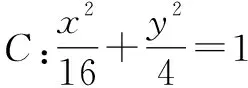
以上两个变式的答案均为8.具体破解过程与以上高考真题的破解方法类似,这里不多加叙述.

5 解后反思

在解决一些平面解析几何的综合问题时,经常从中挖掘相应的平面几何内涵,抽象出对应的平面几何性质,通过合理的直观想象与数形结合,将平面几何融入到平面解析几何中去.通过平面几何的直观性,可以在一定程度上减少数学运算,优化解题过程,形成“数”与“形”之间的转化与变形,为问题的快速解答与优化提供更加便捷的途径,这也是处理平面解析几何综合问题中经常采用的方法.

利用平面几何知识解决平面解析几何综合问题,可以减少平面解析几何的运算量,发散数学思维,有效拓展解题思路,合理利用数形结合与直观想象,从而优化数学解题过程,提升数学解题能力,培养数学核心素养.