第一性原理计算Mo浓度对Mo掺杂BiVO4光催化性能的影响

苟 杰, 熊明姚, 张志远, 吴征成, 苏 欣

(1.伊犁师范大学 物理科学与技术学院, 伊宁 835000 2.伊犁师范大学 新疆凝聚态相变与微结构实验室, 伊宁 835000)

1 引 言

BiVO4是迄今为止报道的性能最高的三元金属氧化物光电阳极材料之一[1]. BiVO4具有三种晶相，即单斜白钨矿结构、四方白钨矿和四方锆石结构. 其中单斜白钨矿结构的BiVO4由于其窄带隙以及稳定性，作为一种高效的可见光驱动光催化剂而备受关注[2-5]. 找到合适的掺杂剂进行掺杂对于提高结构的相关性能至关重要[6，7].

单斜晶系BiVO4具有良好的光学吸收性能以及相对于H/H2O和O/H2O氧化还原电位的合理带边. 其中Park等[8]采用实验加理论的方法研究了W和Mo共掺BiVO4，结果表明，在BiVO4光催化剂中连续掺杂W和Mo，可以提高光催化剂效率. Ding等[9]采用第一性原理计算研究了掺杂IB金属(Cu、Ag和Au)对其光催化活性的影响，发现只有Cu的掺杂对提高单斜晶系BiVO4的光催化活性有积极的作用. Regmi等[10]的制备了Ni掺杂BiVO4半导体材料，Ni掺杂BiVO4样品都比本征BiVO4表现出更好的性能，用于废水处理的光催化性能增强. Zhang等[11]采用Y3+掺杂BiVO4粉末并证明其掺杂体系是一种高效的光催化剂，可用于水分解和烃类气体降解. Toprek等[12]采用第一性原理研究了W掺杂BiVO4的光催化活性，以W原子取代BiVO4中的V原子，带隙随着浓度的增加而增加，带隙变宽，W掺杂BiVO4的吸收系数在可见光区域内得到明显提升. Luo等[13]系统地研究了Mo6+、W6+、Sn4+掺杂BiVO4的不同掺杂位置及其光电化学性质. 结果表明，Mo6+或W6+掺杂的BiVO4具有更高的光电流，而Sn4+掺杂的BiVO4的光电流没有明显变化. 还利用拉曼光谱和X射线光电子能谱分析了BiVO4晶格中的掺杂位置，发现Mo或W取代的是BiVO4中的V位.

综上所述，金属掺杂不论是在实验还是理论方面都有非常丰富的研究基础，而不同浓度的Mo对BiVO4光催化性能的影响在理论方面还未被研究过. 所以，本文采用第一性原理研究不同浓度的Mo掺杂BiVO4的电子结构、光学性质和光催化性能，从而了解不同浓度的Mo对BiVO4体系光催化性能变化的潜在机制.

2 理论模型与计算方法

如图1所示，构建了一个具有2×2×1的几何结构BiVO4超胞，其中的原子总数为96，具体有16个Bi、16个V和64个O原子. 图1中的红色原子，紫色原子和灰色原子分别为O，Bi和V. 分别采用1，2和4个Mo原子掺杂替换图中V原子. 图中标记的1-4就是Mo原子替代的位置，即1个Mo原子时，选择1位置；2个时，选1和2位置；4个时，选1-4位置. 所研究的四种体系可表示为BiMoxV1-xO4(x=0，0.0625，0.125，0.25).

图1 超晶胞掺杂模型：BiVO4Fig. 1 Doping model of supercell：BiVO4

本文利用MS 8.0软件中的CASTEP对不同浓度的Mo掺杂BiVO4体系的性质进行计算模拟[14，15]. 优化结构和最稳定几何体的相应总能量计算基于广义梯度近似(GGA)函数和Perdew-Burke-Ernzerhof(PBE)校正[16]. 采用平面波基组描述各个原子的价层，即O(2s22p4)、Bi(5d106s26p3)、V(3p64s23d3)和Mo(4p64d55s1). 采用2×2×3的k点网格进行布里渊区积分[17]，平面波截止能量400 eV，能量误差为1×10-5eV/atom，最大力0.03 eV/Å，公差位移0.0001 nm，应力偏差0.05 GPa.

3 结果与讨论

3.1 几何优化结果

表1是本征BiVO4和不同浓度的Mo掺杂BiVO4的晶格常数、总能量以及形成能. 本征BiVO4的晶格常数a=7.317 Å，b=11.638 Å，c=5.174 Å. 与实验值a=7.253 Å，b=11.702 Å，c=5.096 Å相比[18]，c的误差为1.5 %，a，b的误差小于1 %，说明选择参数的正确性.

表1 BiVO4掺杂前后的晶格常数、总能量以及形成能

通过计算缺陷形成能来检验BiVO4掺杂体系的稳定性. 其计算公式如下[19]：

(1)

3.2 能带结构分析

图2是BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种体系的能带结构图，由图2(a)可得，本征BiVO4的带隙值为Eg=2.123 eV，价带顶和导带底位于不同的高对称点，所以，单斜相BiVO4为间接带隙. 这与其他科研工作者计算所得的间接带隙值(Eg=2.24 eV)吻合[9]，说明计算BiVO4参数设置的合理性. 根据BiMo0.0625V0.9375O4的能带结构图可得，由于导带底穿过费米能级(EF)，说明BiMo0.0625V0.9375O4具有n型半导体特性，BiMo0.0625V0.9375O4的带隙值增加为2.142 eV. 同理，观察BiMo0.125V0.875O4和BiMo0.25V0.75O4的能带结构图，我们可以发现，掺杂后的BiMo0.125V0.875O4和BiMo0.25V0.75O4同样具有n型半导体特性，带隙值进一步增加为2.160 eV和2.213 eV. 所以，单斜相BiVO4的带隙随着Mo浓度的增大而增大，BiMo0.25V0.75O4达到最大带隙为2.213 eV，Mo掺杂BiVO4后的导带全部向低能量区域移动从而越过费米能级形成n型半导体.

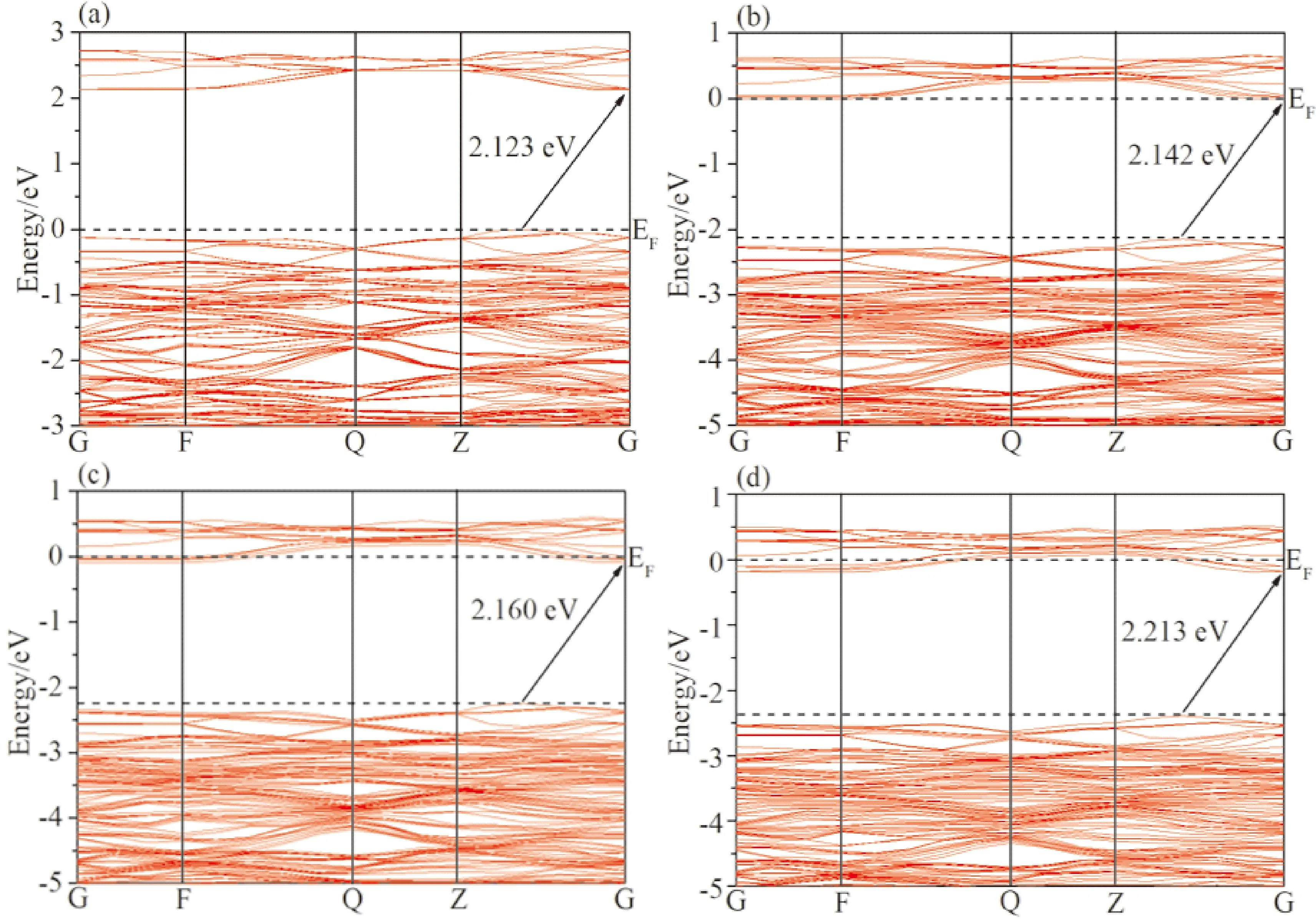
图2 能带结构：(a)BiVO4；(b)BiMo0.0625V0.9375O4；(c)BiMo0.125V0.875O4；(d)BiMo0.25V0.75O4Fig. 2 Band structures：(a)BiVO4；(b)BiMo0.0625V0.9375O4；(c)BiMo0.125V0.875O4；(d)BiMo0.25V0.75O4

3.3 态密度分析

如图3a-d所示，绘制了本征BiVO4和BiMoxV1-xO4(x=0.0625，0.125，0.25)掺杂体系的总态密度图(TDOS)和分波态密度图(PDOS). 本征BiVO4的TDOS和PDOS绘制在图4a中. 其中0 eV处的垂直点线为费米能级. 在-25～-15 eV范围内，TDOS主要是由O 2s和少量的V 3d以及极少量的Bi 6s和6p贡献. 在-15～-5 eV的能量范围内，TDOS几乎完全是由Bi-6s提供，当然还有着微量的O 2p为TDOS贡献. 价带中BiVO4态密度在-5至0 eV范围内，主要是Bi 6p，V 3d和O 2s以及少量的Bi 6s贡献的. 导带中BiVO4态密度，主要是由Bi 6p和V 3d贡献. 对于BiMo0.0625V0.9375O4体系，从图3b可以看出，在导带底部形成了Mo 4d的局域态，整个态密度向低能区域移动，导带底部越过费米能级，形成n型半导体特性，这与能带结构得到的结果一致，说明分析的正确性. 而对于BiMo0.25V0.75O4和BiMo0.125V0.875O4体系，随着Mo浓度的增加(图3c和d)，Mo 4d态的密度增加，在导带底部有更多的Mo 4d占据态. 同时，随着Mo浓度的增加，导带底部越过费米能级越多越明显，这两种掺杂体系同样具有n型半导体特性，与能带结构结果吻合.

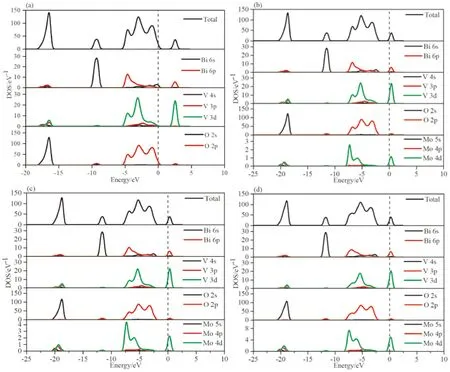
图3 态密度：(a)BiVO4；(b)BiMo0.0625V0.9375O4；(c)BiMo0.125V0.875O4；(d)BiMo0.25V0.75O4Fig. 3 Densities of state：(a)BiVO4；(b)BiMo0.0625V0.9375O4；(c)BiMo0.125V0.875O4；(d)BiMo0.25V0.75O4

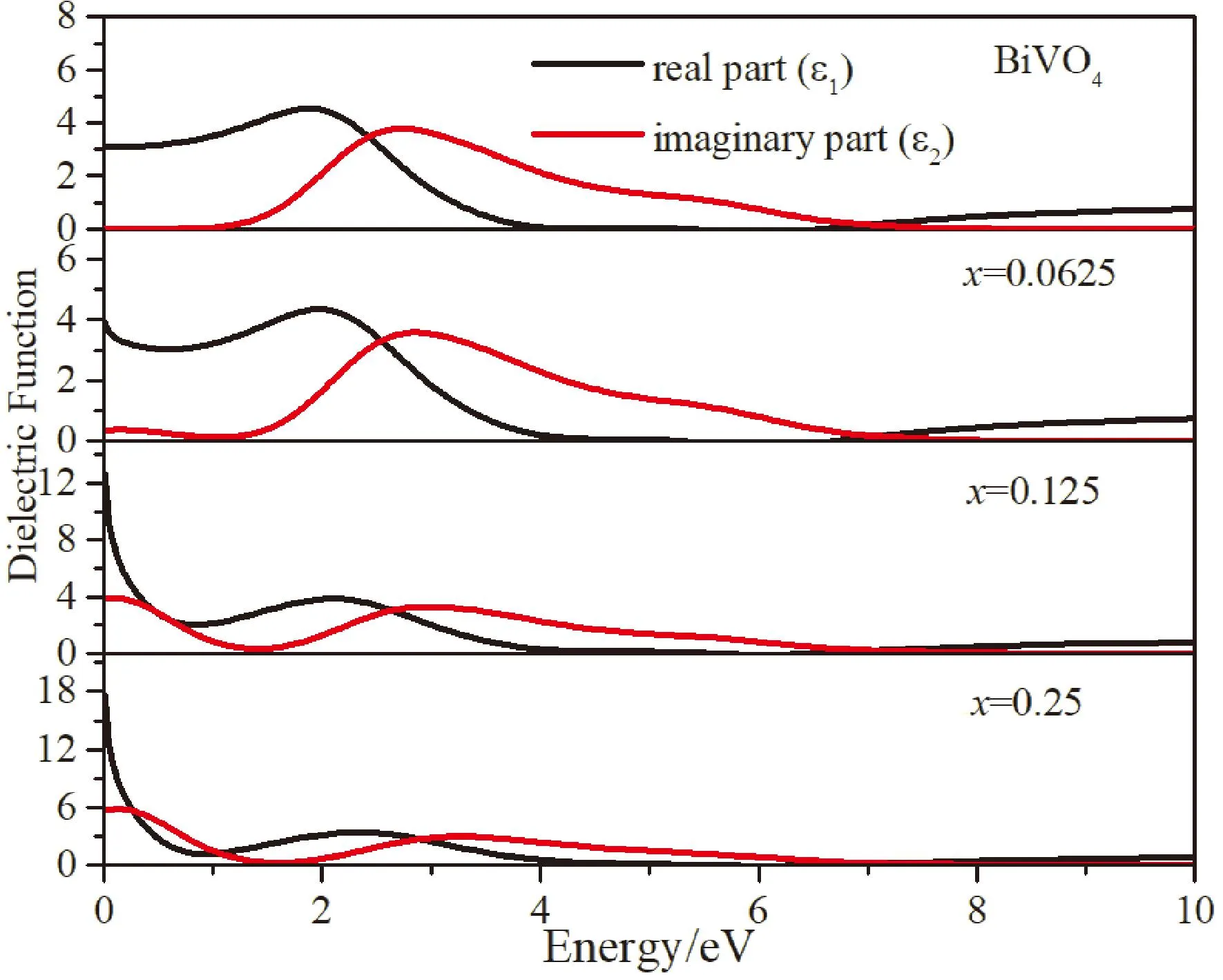
图4 介电函数Fig. 4 Dielectric functions

3.4 光学性质分析

介电函数的虚部ε2(ω)由占据和未占据电子态之间的动量矩阵元素计算得出. 实部ε1(ω)由虚部ε2(ω)通过Kramers-Kronig变换导出. 所有其他光学常数，如吸收系数α(ω)和反射率R(ω)，都是从ε1(ω)和ε2(ω)推导出来的. 通过ε1(ω)和ε2(ω)的相关函数可以得到吸收系数α(ω)和反射系数R(ω)[20]：

(2)

(3)

根据下图4所示为BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种体系的介电函数图，图4中黑线和红线分别为体系介电函数的实部和虚部. 将零能量下介电函数实部的值称为静态介电常数，用ε1(0)表示. 从图中可以看出BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种体系的介电常数分别为3.08，3.90，12.7和17.50，由此显而易得的是掺杂后的静介电常数随着Mo原子的浓度呈现增大的趋势，这意味着通过Mo掺杂BiVO4体系后新诱导的电子态将导致更多的电荷转移，其中BiMo0.25V0.75O4静介电常数最大，效果最好. 介电函数的虚部反映的是不同能量光子的吸收特性，从图中可以看出掺杂后BiVO4体系峰值相较于本征BiVO4峰值有所降低. 对于低能量区域，本征BiVO4的虚部为零，随着Mo原子浓度的增加，BiVO4的虚部逐渐增大.

图5是本征BiVO4和BiMoxV1-xO4(x=0.0625，0.125，0.25)掺杂体系的反射光谱图. 图中本征BiVO4在能量为6.45 eV时达到最大值0.261，BiMo0.0625V0.9375O4在能量为6.52 eV时的最大值为0.260，BiMo0.125V0.875O4的BiMo0.25V0.75O4的最大值分别为0.328和0.392. 当能量大于7 eV，四种BiVO4体系的反射曲线趋势趋于一致，BiMo0.125V0.875O4和BiMo0.25V0.75O4这两种掺杂体系的最大值明显高于本征BiVO4. 可以看出BiMoxV1-xO4(x=0.0625，0.125，0.25)三种掺杂体系在低能量区域内的反射光谱提升明显，其中，BiMo0.25V0.75O4体系最高.

图5 反射光谱Fig. 5 Reflectance spectra

图6是BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种体系的吸收光谱图，从图中可以看出，本征BiVO4的吸收系数在150 nm—1100 nm不为零，并且通过增加Mo原子的浓度吸收系数具有向较短波长移动的趋势. 对于波长大约在400—800 nm，吸收系数随Mo浓度的增加而减小，但对于波长大于1100 nm时，可以清楚的观察到光吸收系数随着Mo浓度的增大而增强. 这表明，BiVO4通过增加Mo原子的浓度，可以更好的利用红外光.

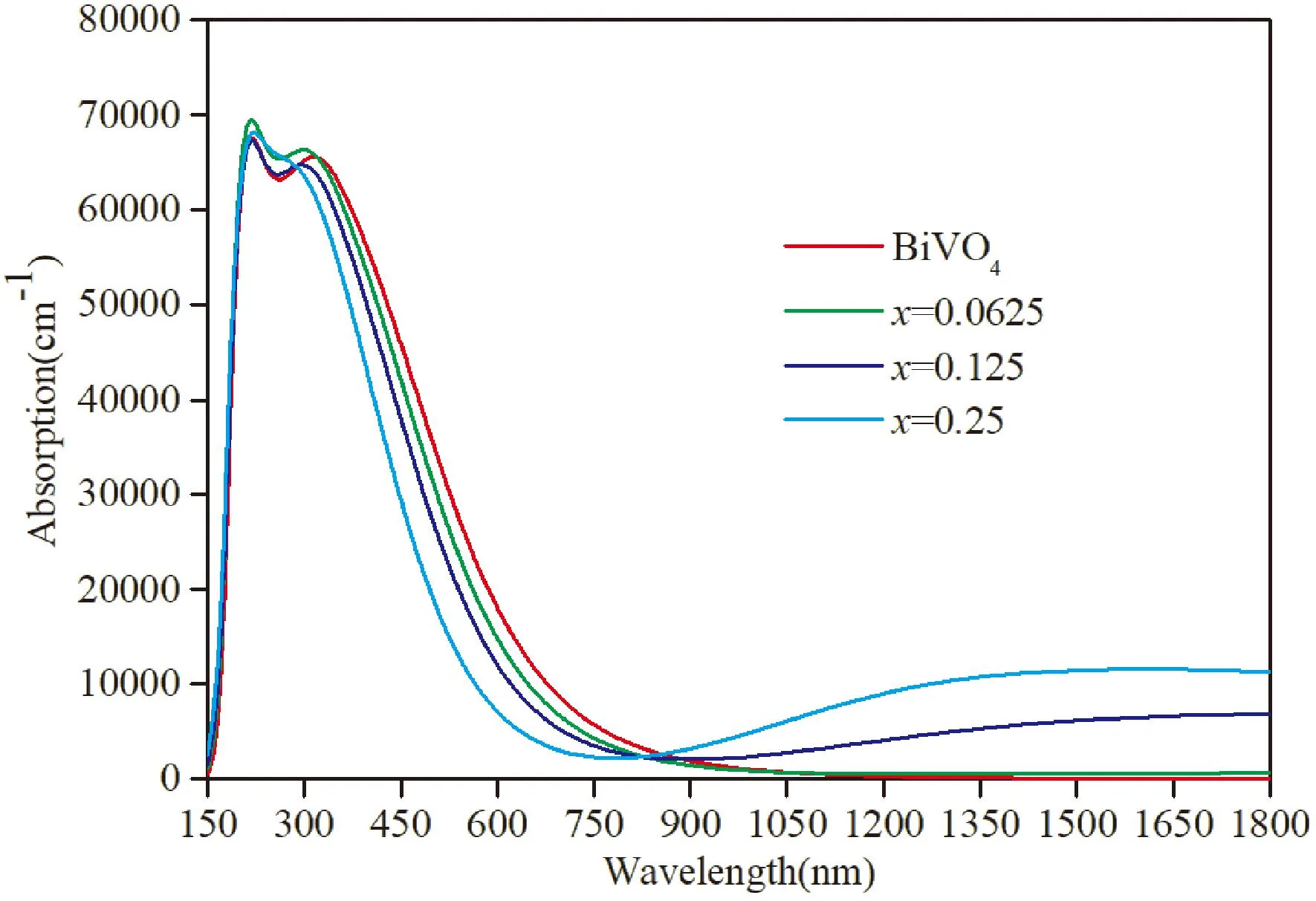
图6 吸收光谱Fig. 6 Absorption spectra

3.5 光催化性能

为了研究本征BiVO4和掺杂BiVO4的光催化活性，半导体的带边位置和吸附物种的氧化还原电位对光催化性能非常重要. 半导体的导带带边的还原电势(ECB)和价带带边的氧化电势(EVB)可以通过以下经验公式得到[21]：

ΕCB=X-Εe-0.5Εg

(4)

ΕVB=Εg+ΕCB

(5)

X为半导体的电负性，Ee为H标度上的自由电子能量(Ee约为4.5 eV)，Eg是对应体系的带隙值.

半导体BiaVbOc的电负性由以下方程式计算[22]：

X=[Xa(Bi)·Xb(V)·Xc(O)]1/(a+b+c)

(6)

式中，a、b和c是化合物中Bi、V和O原子的数量，X(Bi)、X(V)和X(O)是组成原子的原子电负性.

类似地，掺杂体系BiaVbOc-dZd的电负性：

X=[Xa(Bi)·Xb(V)·Xc-d(O)·Xd(Z)]1/(a+b+c)

(7)

式中，d是体系中Mo原子的数量，X(Z)是对应掺杂原子Mo的电负性，计算所得数据列于表2.

表2 计算的本征BiVO4和掺杂BiVO4的电负性X和带边位置ECB和EVB，Eg是计算的带隙.

由表2可知，BiMoxV1-xO4(x=0，0.0625，0.125，0.25)的导带电势分别为0.4745 eV，0.4690 eV，0.4650 eV和0.4425 eV. 这些结构的价带电势分别为2.5975 eV，2.6110 eV，2.6250 eV，2.6615 eV. 图7所示为本征BiVO4和BiMoxV1-xO4(x=0.0625，0.125，0.25)作为光催化剂的示意图. 可以看出，四种体系的价带电位都比O2/H2O(1.24 eV)都大，能够氧化H2O生成O2. 在BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种结构中，BiMo0.25V0.75O4氧化生成O2的能力最高，本征BiVO4体系氧化生成O2的能力是最低的.

4 结 论

本文基于第一性原理计算研究了V晶格上掺杂原子Mo的浓度对具有单斜白钨矿BiVO4的电子结构、光学性质和光催化活性的影响. 浓度效应表现如下：通过增加Mo的浓度，BiVO4的带隙增大. BiMoxV1-xO4(x=0，0.0625，0.125，0.25)四种体系均是间接跃迁形式，三种BiVO4掺杂体系具有n型半导体特性. BiMoxV1-xO4(x=0.0625，0.125，0.25)体系的静介电常数大于本征BiVO4. 光吸收系数显示BiVO4通过增加Mo原子的浓度，可以更好的利用红外光. 而在四种体系当中，BiMo0.25V0.75O4氧化生成O2的能力是最高的.