稀土X (X=La、Ce、Pr、Nd)修饰单层h-MoS2的NO气敏性

薛丽丽, 高 静, 赵丽瑾, 王 芳, 王 伟, 张一鸣

(1. 山东省产品质量检验研究院, 济南 250100; 2. 吉林大学 微纳传感材料与器件实验室,长春 130012)

1 引 言

随着工业的快速发展，化石燃料的消耗与日俱增，与之伴随的是包括NO、NO2、SO2等在内的小分子气体对于环境的污染越来越严重，对人类的健康和工农业生产带来严重危害[1，2].据报道，吸入超过50 ppb量级浓度的NO气体就会损伤人的中枢系统[3].此外，NO还可以通过氧化转化为毒性更大的二氧化氮气体(NO2)[4].除了作为一种常见的空气污染物外，NO还能促进各种疾病的传染，即便是在低浓度下也会在一定程度上加速病毒的传染[5].因此在低浓度状态即能检测到NO存在对人们身体健康非常有利.目前对于气体浓度的检测有两种方法，一种是通过化学检验法检测，但是效率相对较低，不适合大规模应用；另外一种是通过专用的分析仪器完成，其原理是基于各种感知原理而设计的气敏传感器[6].作为传感器家族中的一员，以半导体材料为基础的气敏传感器具有灵敏度高、稳定性好、响应和恢复时间短等优点，是制作气敏传感器的理想材料.但是传统的半导体气敏传感器同时还存在着工作温度高、寿命短等缺点，制约了其在工业和生活中的应用[7].单层 h-MoS2是典型的过渡金属硫化合物，具有类石墨烯结构.和传统半导体材料相比，h-MoS2具有比表面积大、优越的化学、物理和电学特性，而且在地壳中储量丰富，是制作气体探测传感器的理想材料[8，9].但是h-MoS2和其他晶体不一样，其表面没有悬挂键[10]，不容易吸附气体小分子，且响应/恢复时间长、低气敏性，因此本征单层h-MoS2无法直接用于气敏传感器的制作.

掺杂是材料改性的一种非常有效的手段，且已经在其他方面得到广泛的应用，Chen等[11]通过F4TCNQ分子修饰MoS2表面明显缩短了对NH3的响应时间.Sharma等[12]将CuO与MoS2形成异质结，能够探测到浓度为5 ppm的NH3气体，且响应/恢复时间仅为17 s/26 s；Cho等[13]用Au掺杂MoS2后电子从Au向MoS2流动，提高了气敏性；Cui等[14]发现SnO2修饰MoS2后对于环境的适应性大大增强；Pham等[15]通过气相化学沉积法(CVD)对MoS2进行Au原子修饰后，其对NO的探测极限降低到0.1ppb；Ma等[16]通过第一性原理计算得到Au，Pt，Pd等贵金属掺杂MoS2能够对能带进行调制，进而影响对NO、NO2的吸附.这些研究结果表明，掺杂或异质结修饰MoS2后电子性质将产生变化，增强了表面自由电子或空穴的面密度，从而影响到对探测气体的气敏性.稀土是调控材料性能的重要的掺杂剂，在工业上有不可替代的作用，由于稀土在改善材料性能方面的优越性，很多国家将稀土列为战略储备物质.Rathi等[17]研究发现La掺杂MoS2后其响应/恢复时间只有未掺杂之前的1/6，且对于NO2的敏感性由3.346 ppm降低到0.627 ppm；Rong等[18]发现Ce掺杂MoS2后氧化电势由1.733 V降低到1.508 V，能够显著提高氧化反应效率.虽然稀土能够对材料的性能进行调节，但是对于MoS2气敏性影响的研究还比较少，Rathi等[17]虽然研究了La掺杂MoS2对NO2气敏性的影响，但是对于其中的机理没有说明.鉴于此，本文将采用基于密度泛函理论的第一性原理研究常见的La、Ce、Pr、Nd四种稀土元素对h-MoS2中的NO气敏性影响，从原子分子层面揭示气敏性调控机理，为设计全新的气敏传感器提供理论依据.

2 计算方法

计算过程采用了基于密度泛函理论的第一性原理[19，20]，交换关联势能采用的是广义梯度近似中的PBE泛函，k点网格密度为8×8×1，超软赝势的截断能是460 eV，总体能量收敛1×105eV/atom，最大应力0.05 GPa.能带、态密度的计算采用的是HSE06杂化泛函[21]，价电子分别为Mo-4p64d55s1、S-3s23p4、N-2s22p3、O-2s22p4.

在自然状态下，体相h-MoS2属于六方晶系，空间群为P63/mmc(图1a).对体相h-MoS2单胞(0001)面进行修剪得到单层h-MoS2(图1b).考虑到掺杂浓度，对a、b两个基矢扩展3倍，得到单层h-MoS2的3×3×1的超晶胞(图1c)，此模型中Mo原子有9个，S原子有18个.为屏蔽相邻单层h-MoS2之间的相互作用，在[0001]方向上设置了20 Å的真空层.所有稀土元素调控和或气体分子吸附都是在此模型上进行的.

图1 计算模型：(a)体相h-MoS2；(b)单层h-MoS2；(c)单层h-MoS2的3×3×1超晶胞Fig. 1 Calculation models：(a)pristine h-MoS2；(b)monolayer h-MoS2；(c)3×3×1 supercell of monolayer h-MoS2

3 结果与讨论

3.1 几何优化

为验证计算方法的可靠性，首先用GGA-PBE对体相h-MoS2进行晶格优化，得到的体相h-MoS2的晶格常数为a=b=3.16 Å，c=12.32 Å，Schonfeld 等[22]通过X射线衍射法测得a=b=3.161 Å，c=12.295 Å，Ataca等人[23]通过第一性原理计算得到a=b=3.17 Å，c=12.41 Å.经过对比发现，本文通过GGA-PBE优化 h-MoS2得到的晶格常数与前人在理论和实验上得到的非常接近，初步判定本文所建模型合理、准确.

3.2 稳定性

对于晶体通常用形成能表征结构的稳定性，形成能是孤立原子结合成晶体时所释放出来的能量，若形成能为负值，表示该掺杂为放热反应，体系能量减小，理论上说明该体系稳定，且形成能越小则说明体系越稳定，掺杂越容易进行；反之则不稳定，不容易掺杂.对于稀土La、Ce、Pr、Nd四种元素掺杂h-MoS2有两种形式，一种是取代Mo原子，一种是取代S原子，通过计算四种稀土元素两种不同取代方式的形成能得到结构的稳定性.公式(1)为稀土取代Mo的形成能，公式(2)为稀土取代S的形成能[24].

Eform1=ETotal-(m-1)μMo-2mμS-μX

(1)

Eform2=ETotal-mμMo-(2m-1)μS-μX

(2)

其中ETotal是掺杂体系的总能量，μMo、μS、μX分别是孤立态的Mo、S、X(X=La、Ce、Pr、Nd)原子的能量，m是结构中的Mo原子个数，2m是结构中的S原子个数.表1即为计算得到的掺杂体系的形成能.

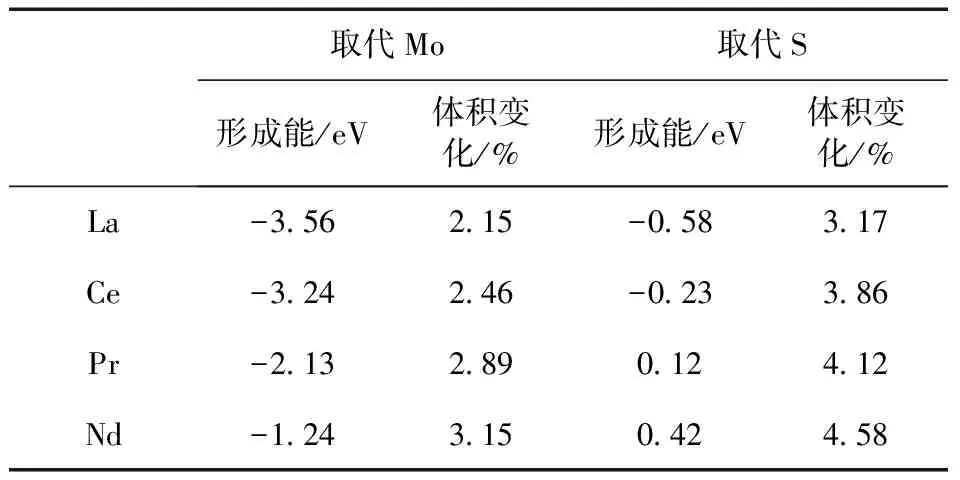
表1 X (X = La，Ce，Pr，Nd)取代Mo、S原子后的形成能

从表1中可以看出，La、Ce、Pr、Nd取代Mo原子后得到的形成能分别为-3.56 eV、-3.24 eV、-2.13 eV、-1.24 eV，结合能为负，说明掺杂体系容易形成且稳定存在.同时还可以看出，随着稀土元素原子序数的增加，体系的形成能在增大，说明稳定性在减弱.La、Ce、Pr、Nd取代S原子后得到的形成能分别为-0.58 eV、-0.23 eV、0.12 eV、0.42 eV，Pr、Nd取代S原子后形成能为正，说明体系不稳定.虽然La、Ce取代S原子后的形成能为负，但是相比于取代Mo原子后的形成能高出很多.出现上述结果主要由两个方面的原因，一是孤立Mo原子的能量为-0.042 eV，而孤立S原子的为-0.056 eV，Mo原子的能量要高于S原子，所以稀土取代Mo后更容易降低体系能量；二是稀土原子的原子半径要大于Mo和S的，所以取代后会导致晶格畸变，通过表1可以看出，取代Mo原子后的体积增大最高达到3.15%，而取代S原子后的体积增大最高达到4.58%，由此看出取代S原子带来的晶格畸变能量要高.综上所述，本项目主要研究La、Ce、Pr、Nd取代Mo原子后的气敏传感性.

为了从电子层面研究掺杂体系的稳定性，本文还计算了掺杂体系的Mulliken布居数和键长.Mulliken布居数是电子在各原子轨道上的分布，能在一定程度上反应化学键的成键情况，两原子间的布局数大说明电子主要局域在两原子之间，更倾向于形成共价键；反之两原子间的Mulliken布居数小说明电子主要局域在各自的原子轨道上，更倾向于形成离子键.表2、表3分别给出了稀土元素取代Mo、S原子后的Mulliken布居数和键长，未掺杂之前的h-MoS2的Mulliken布居数为0.27，X(X=La、Ce、Pr、Nd)取代Mo原子后的Mulliken布居数分别为0.35、0.33、0.32、0.32，相比于未掺杂前，Mulliken布居数增大，说明掺杂后更倾向于在X-S之间形成共价键，有利于体系稳定，与形成能得到的结论一致.同时，X-S之间的化学键长相比于未掺杂前的也增加了，导致了晶格畸变，体积增大，与表1所得结论一致.X(X=La、Ce、Pr、Nd)取代S原子后的Mulliken布居数分别为0.31、0.28、0.27、0.25，其中Mo-La、Mo-Ce之间的Mulliken布居数要比未掺杂之前的大，说明掺杂后结构稳定，而Mo-Pr、Mo-Nd的Mulliken布居数要比未掺杂之前的h-MoS2的小，共价效应减弱，稳定性降低，与表1计算出的形成能为正结论一致.

表2 X (X = La，Ce，Pr，Nd)取代Mo原子后的Mulliken布居数和键长

3.3 吸附特性

单层h-MoS2对NO的吸附可以用吸附能表示，

Eabs=EMoS2+NO-EMoS2-ENO

(3)

吸附能表征气体分子在材料表面的稳定性和反应的难易程度，吸附能为负表示能够吸附，且吸附稳定；反之则表示不能吸附.公式(3)中Eabs、EMoS2+NO、EMoS2、ENO分别表示体系吸附能、吸附体系总能量、单层h-MoS2能量、孤立NO分子能量.分子吸附后电荷转移数量可以通过Hirshfeld电荷分析方法得到，该方法可以确定气体分子在吸附在基体上后是得到还是失去电子，从而分析基体电阻的变化情况和气敏性.每个原子的电荷ΔQ可以通过计算密度ρ(r)和电子密度ρ0(r)得到[25]，其表达式如公式(4).

(4)

本文以NO分子作为吸附对象来研究单层h-MoS2的气敏性.为了寻找最稳定的吸附构型，分别计算了Mo、S以及X(X=La、Ce、Pr、Nd)原子顶部吸附位的吸附性质，即TMo，TS1，TS2、Tx，其中TS1和TS2分别是与X原子直接成键的S和没有成键的S(如图2所示).通过对比上述4种不同吸附位点的吸附能(Eabs)、吸附距离(d)和Hirshfeld转移电荷(ΔQ)来确定最稳定的吸附位点.吸附能能够判断吸附强弱；吸附距离是吸附的气体分子与吸附点位之间的距离，其值越小说明相互作用越大，如果吸附距离小于吸附物到基底材料最近两原子共价键长，则容易形成化学吸附，反之则为物理吸附；Hirshfeld电荷分析可以定量描述系统的电荷转移情况，正值代表基体在吸附反应中作为电荷受体，反之则为电荷供体.

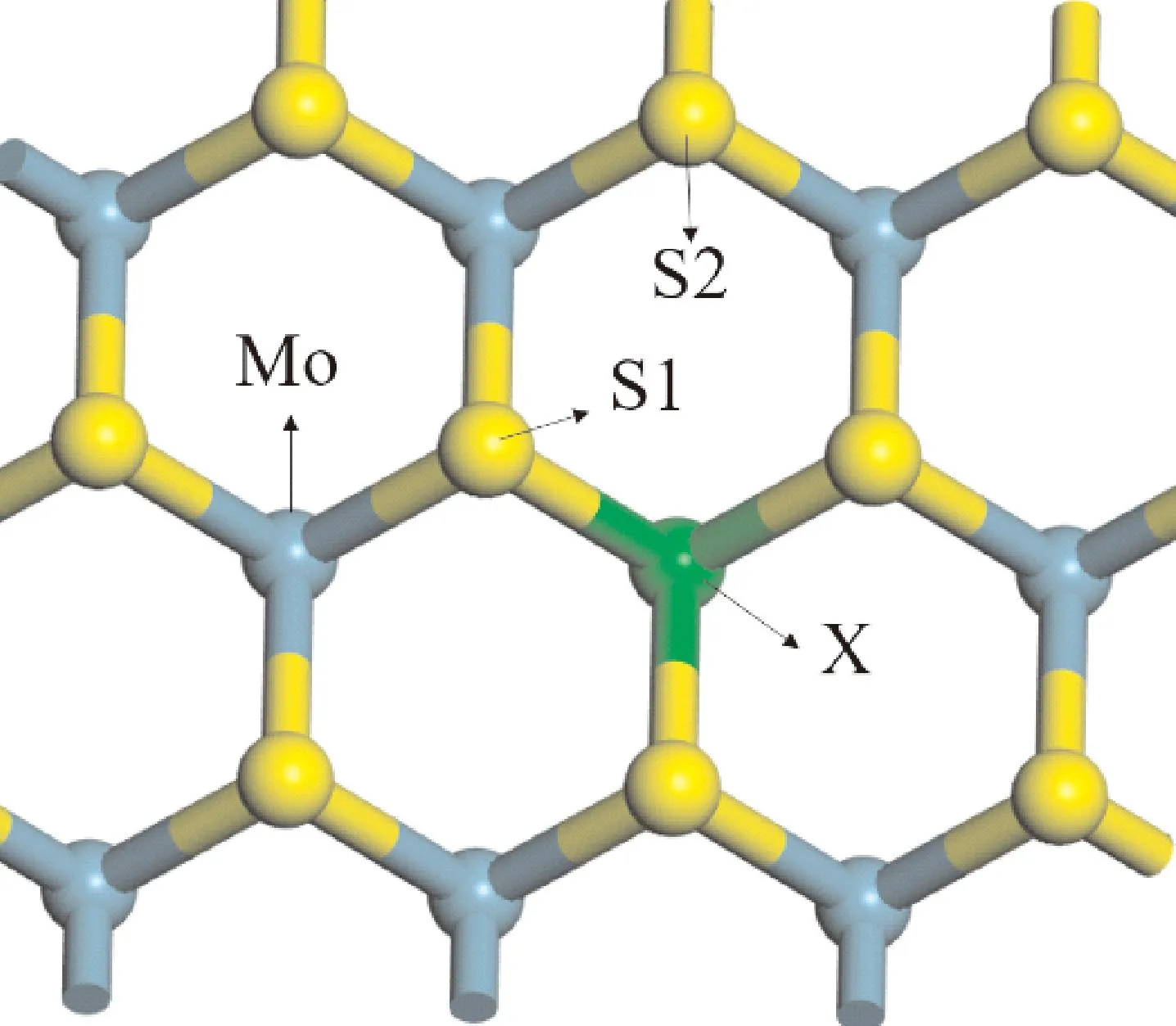
图2 NO吸附h-MoS2不同位置示意图Fig. 2 Diagram of NO adsorbed on different positions of h-MoS2

表4是稀土掺杂单层h-MoS2后NO的吸附能、吸附距离和Hirshfeld转移电荷，可以看出未掺杂之前的单层h-MoS2吸附能在-0.76 eV左右，而掺杂X(X=La、Ce、Pr、Nd)后的吸附能均值分别为-0.95 eV、-1.02 eV、-0.83 eV和-0.81 eV，可以看出掺杂后的吸附能要比未掺杂之前的小，所以掺杂能够增强NO的吸附能力.La掺杂后NO吸附在La原子顶部位置的吸附能为-1.215 eV，相比其他三个吸附位置吸附能最小，因此对于NO的吸附最稳定，对于两个不同位置的S原子，与La直接相连接的S原子S1顶部的NO吸附能为-0.954 eV，低于S2顶部的NO吸附能(-0.758 eV)，因此NO更倾向于在S1顶部吸附；La掺杂后的吸附距离最小为La-NO之间的吸附(2.475 Å)，远小于单层h-MoS2和NO分子间两个最近原子的共价键长(3.195 Å)，推断La-NO之间属于化学吸附，而该吸附位的Hirshfeld转移电荷为0.213e，进一步证实了La与NO分子间吸附较强.Ce掺杂后NO吸附在Ce原子顶部位置的吸附能为-1.225 eV，相比其他三个吸附位置吸附能最小，因此对于NO的吸附最稳定，对于两个不同位置的S原子，与Ce直接相连接的S原子S1顶部的NO吸附能为-1.142 eV，低于S2顶部的NO吸附能(-0.896 eV)，NO更倾向于在S1顶部吸附；Ce掺杂后的吸附距离最小为Ce-NO之间的吸附(2.854 Å)，小于单层h-MoS2和NO分子间两个最近原子的共价键长(3.054 Å)，推断Ce-NO之间属于化学吸附，而该吸附位的Hirshfeld转移电荷为0.325e，进一步证实了Ce与NO分子间吸附较强.同时，由于MoS2属于n型半导体，而掺杂La、Ce后Hirshfeld转移电荷皆为正，说明电荷向基体表面转移，降低了电阻，提高了气敏性.Pr掺杂后NO吸附在Pr原子顶部位置的吸附能为-0.912 eV，相比其他三个吸附位置吸附能要小，但是其他三个不同吸附位的吸附能也都在-0.8 eV左右，差别不是很明显，对于两个不同位置的S原子，与Pr直接相连接的S原子S1顶部的NO吸附能为-0.856 eV，低于S2顶部的NO吸附能-0.794 eV，能量差别不是很明显；Pr掺杂后的吸附距离最小为Pr-NO之间的吸附(3.405 Å)，大于单层h-MoS2和NO分子间两个最近原子的共价键长(3.186 Å)，推断Pr-NO之间属于弱van der Waals力下的物理吸附，而该吸附位的Hirshfeld转移电荷为-0.056e，进一步证实了Pr与NO分子间吸附较弱.Nd掺杂体系与Pr掺杂体系具有类似的特点，但是对于两个不同位置的S原子，与Nd直接相连接的S原子S1顶部的NO吸附能为-0.745 eV，而S2顶部的NO吸附能-0.812 eV，NO更倾向于吸附在S2顶部，但是能量差别不是很明显；Nd掺杂后的吸附距离最小为S-NO之间的吸附距离(3.516 Å)，大于单层h-MoS2和NO分子间两个最近原子的共价键长(3.215 Å)，推断S-NO之间属于物理吸附.同时可以看出，掺杂Pr、Nd后Hirshfeld转移电荷皆为负，说明电荷向NO转移，增加了电阻，降低了气敏性.

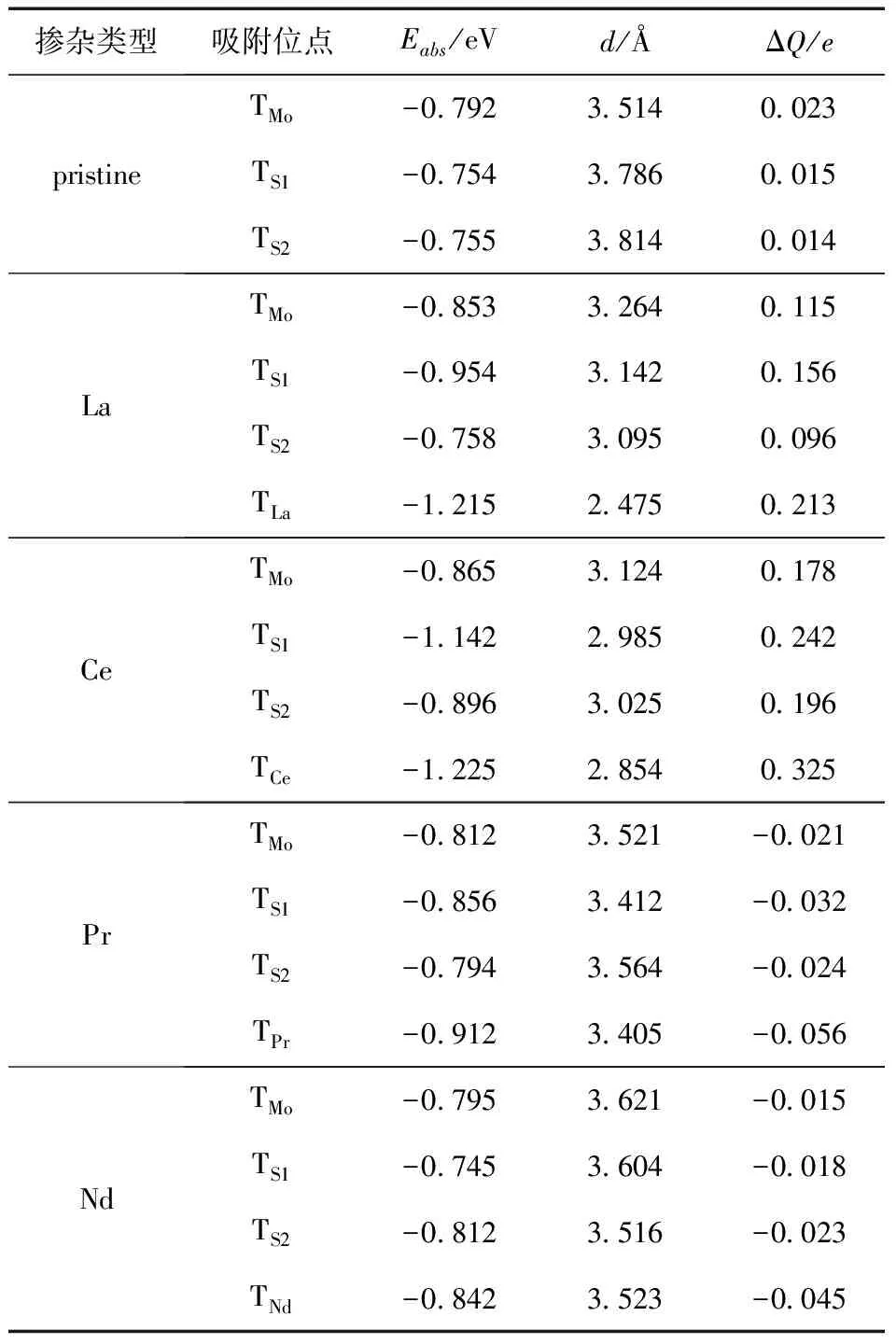
表4 X (X = La，Ce，Pr，Nd)修饰单层h-MoS2吸附NO的吸附能、吸附距离和Hirshfeld转移电荷

对体系施加电场能够改变体系电荷的布局，从而改变材料性质，改善气敏性.本文在原有计算模型的基础上沿[0001]方向施加了0.001 a.u.的电场.表5是电场调控单层h-MoS2吸附NO的吸附能、吸附距离和Hirshfeld转移电荷，对比本征h-MoS2可以看出未施加电场前吸附能平均值为-0.76 eV，施加电场后为-0.78 eV，吸附能略有增加，但是增加幅度非常有限，同时吸附距离和Hirshfeld转移电荷变化也不是很明显，所以施加电场对本征h-MoS2吸附NO能力的改善作用有限.对La掺杂体系施加电场后，NO吸附在La原子顶部位置的吸附能为-1.425 eV，相比于未加电场前的-1.215 eV增长了16%，四个不同吸附位的吸附距离分别为3.025 Å、2.954 Å、3.021 Å、2.324 Å，相比未施加电场前的减小非常明显，因此对于NO的吸附更加稳定.对Ce掺杂体系施加电场后，NO吸附在Ce原子顶部位置的吸附能为-1.296 eV，相比于未加电场前的-1.225 eV基本没有变化，吸附距离为3.121 Å，未施加电场之前为3.025 Å，相比略有增加，但是仍然保持化学吸附特征.对Pr掺杂体系施加电场后，NO平均吸附能为-0.958 eV，而未加电场前的平均吸附能为-0.833 eV，降低了约12.5%，吸附更容易进行；施加电场后，平均吸附距离为3.06 Å，具有明显的化学吸附特性，而未加电场前属于弱van der Waals力下的物理吸附；施加电场后，Hirshfeld转移电荷为正值，NO向基体转移电荷，减小了基体电阻，提高了气敏性，而未加电场前为负，基体向NO转移电荷，增加了基体电阻，所以施加电场对Pr掺杂h-MoS2的影响非常明显.对Nd掺杂体系施加电场后Nd原子顶部位置的吸附能为-0.862 eV，相比于未加电场前的-0.842 eV基本没有变化，吸附距离为3.51 Å，未施加电场之前为3.523 Å，相比略有减小，但是仍然属于弱van der Waals力下的物理吸附，影响不是很明显.

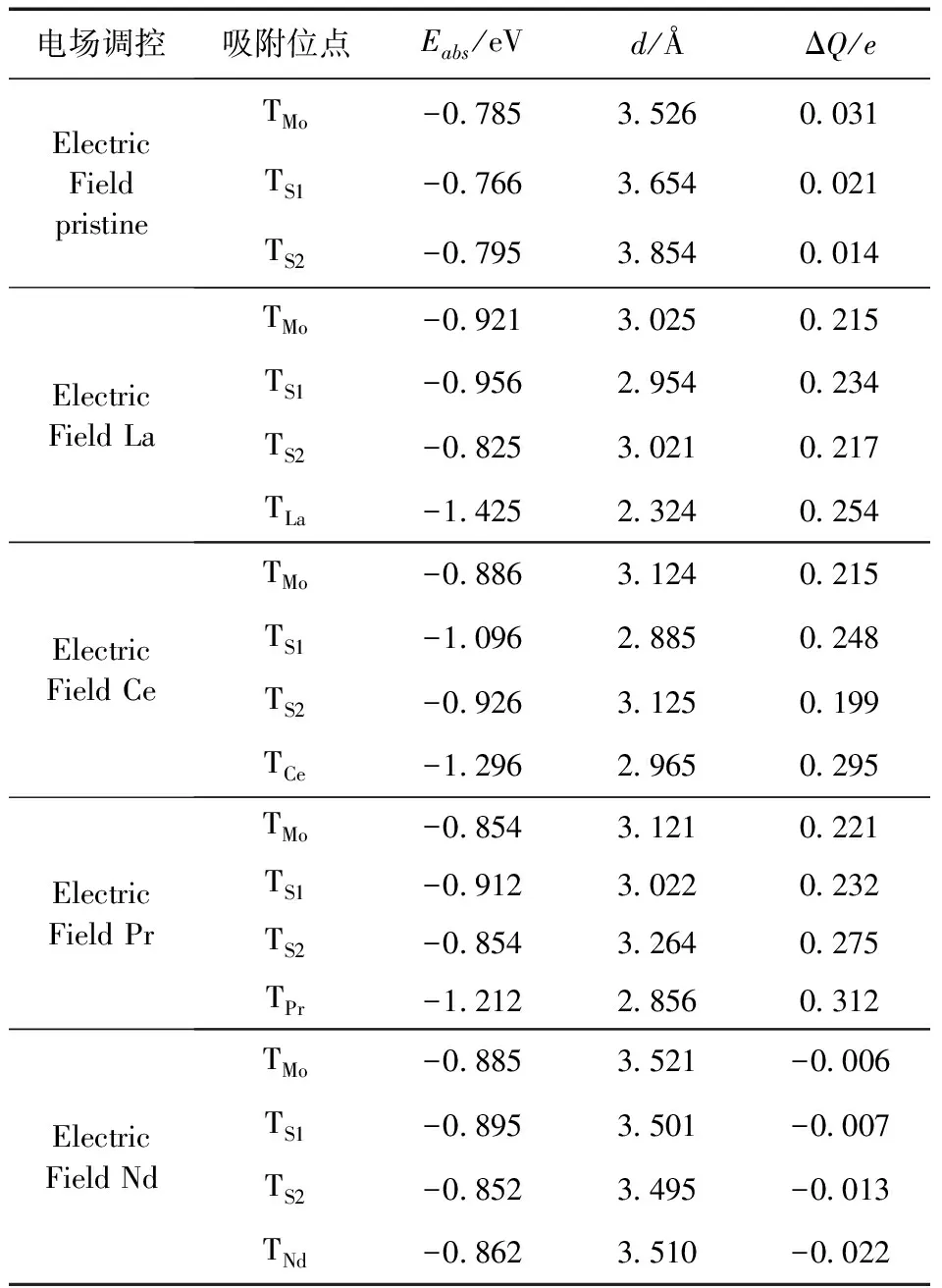
表5 电场调控单层h-MoS2吸附NO的吸附能、吸附距离和Hirshfeld转移电荷

3.4 功函数

功函数(WF)为单个电子由固体的内部移至表面真空中所需要的最小能量，是描述物质中电子逃离难易程度的重要参数之一.传感器在吸附气体后会引起功函数变化，吸附前后功函数变化越大说明气敏性越高，有利于检测[26].功函数表示为公式(5).

WF=-eΦ0-EF

(5)

其中e是电子电量，Ф0是真空静电势，EF是费米能级.图3是稀土掺杂单层h-MoS2功函数，图3(a)是没有施加电场的功函数，横坐标对应的是四种不同的吸附位置.在Mo原子顶部吸附位置，本征体系功函数为5.21eV，而X(X=La、Ce、Pr、Nd)掺杂的功函数分别为4.86 eV、4.75 eV、5.15 eV和5.24 eV，可以看出La和Ce掺杂后能明显改变功函数的大小，而Pr和Nd掺杂对功函数的改变很小，在S1、S2以及X(X=La、Ce、Pr、Nd)顶部吸附NO后也有类似的规律.根据吸附前后功函数变化越大说明气敏性越高，有利于检测的规律可知，La和Ce掺杂后能明显改变单层h-MoS2的气敏性，与吸附能、吸附距离和Hirshfeld转移电荷得出的结论非常相似.图3(b)是施加电场后的功函数，对比图3(a)(b)两个图形可以看出，施加电场后的功函数略有增加.在Mo原子顶部吸附位置，本征体系功函数为5.32 eV，而X(X=La、Ce、Pr、Nd)掺杂的功函数分别为4.95 eV、5.09 eV、4.96 eV和5.22 eV，可以看出Ce和Pr掺杂后能明显改变功函数的大小，而Ce和Nd掺杂对功函数的改变很小，在S1、S2以及X(X=La、Ce、Pr、Nd)顶部吸附NO后也有类似的规律.

图3 X (X = La，Ce，Pr，Nd)掺杂单层h-MoS2的功函数：(a)没有电场；(b)施加电场Fig. 3 The work functions of X (X = La，Ce，Pr，Nd)doped monolayer h-MoS2：(a)no electric field；(b)with electric field

3.5 伏安特性

为了更直观地计算稀土掺杂对单层h-MoS2气敏性的影响，利用非平衡格林函数(NEGF)方法建立了载流子输运模型[27]，研究NO与单层h-MoS2吸附时的伏安特性.理论上稀土元素顶部吸附位的气敏性最强，所以关于伏安特性的计算就以四种稀土元素顶部吸附展开，电压偏压范围为0-2 V.图4即为伏安特性曲线，可以看出未施加电场时(图4a)随着电压的增大，La、Ce两掺杂体系的电流分别由0增大到5.3 μA和4.8μA，而Pr、Nd两掺杂体系的电流分别仅仅由0增大到2.2 μA和1.2 μA，所以La、Ce掺杂对于体系敏感性的影响比较明显，与Hirshfeld转移电荷的研究结果一致.图4(b)是施加电场后(图4a)伏安特性曲线，施加电场后Ce体系的电流由0增大到6.5 μA，相比未施加电场前敏感性增强，同时Pr体系的电流由0增大到4.8 μA，气敏性也得到明显的提升，与Hirshfeld转移电荷的结论一致.

图4 X (X = La，Ce，Pr，Nd)顶部吸附位的伏安特性曲线：(a)没有电场；(b)施加电场Fig. 4 The V-I curves of top adsorption site of X (X = La，Ce，Pr，Nd)：(a)no electric field；(b)with electric field

4 结 论

基于密度泛函理论的第一性原理，研究了X(X=La、Ce、Pr、Nd)稀土元素对单层h-MoS2的NO气敏性的影响，得到如下结论：

(1)La、Ce、Pr、Nd取代Mo原子后得到的形成能分别为-3.56 eV、-3.24 eV、-2.13 eV、-1.24 eV，说明掺杂体系容易形成且稳定存在；而取代S原子后得到的形成能虽然除Nd掺杂体系外也都为负，但是能量要比取代Mo原子高，因此La、Ce、Pr、Nd取代Mo原子体系最为稳定.

(2)La、Ce、Pr、Nd取代Mo原子后的Mulliken布居数分别为0.35、0.33、0.32、0.32，相比于未掺杂前，Mulliken布居数增大，说明掺杂后更倾向于在X-S之间形成共价键，有利于体系稳定.

(3)NO吸附在La、Ce原子顶部位置的吸附能为-1.215 eV，-1.225 eV，吸附距离分别为2.475 Å、2.854 Å，具有明显的化学吸附特征，Hirshfeld转移电荷分别为0.213e和0.325e，具有明显的受体特征，降低了电阻，提高了气敏性.施加电场后能有效提高Pr掺杂体系的吸附强度，增大Hirshfeld转移电荷，所以电场对Pr掺杂体系的影响最为明显.

(4)本征结构功函数为5.21 eV，X(X=La、Ce、Pr、Nd)掺杂的功函数分别4.86 eV、4.75 eV、5.15 eV和5.24 eV，因此La和Ce掺杂后能明显改变功函数的大小，而Pr和Nd掺杂对功函数的改变很小，施加电场后对Pr的影响非常明显.

(5)通过分析掺杂体系的伏安特性曲线，La、Ce两掺杂体系的电流分别由0增大到5.3 μA和4.8 μA，而Pr、Nd两掺杂体系的电流分别仅仅由0增大到2.2 μA和1.2 μA，所以La、Ce掺杂对于体系敏感性的影响比较明显.