利用多周期空间非均匀啁啾场产生单个短阿秒脉冲

韩岳峰, 张刚台, 白婷婷, 张依琳, 张 倩, 赵 曦

(1.宝鸡文理学院 物理与光电技术学院, 宝鸡 721016; 2.宝鸡文理学院 数学与信息科学学院, 宝鸡 721013;3.黔南民族师范学院 物理与电子科学学院, 都匀 558000)

1 引 言

阿秒光脉冲的出现和发展为微观动力学的研究带来前所未有的时间分辨率，使得人们深入研究物质内部电子的超快动力学过程，包括电子的跃迁、电离和驰豫过程[1]等成为可能. 目前通过超强超快激光与原子、分子相互作用产生的高次谐波是实验上获得单阿秒脉冲的有效途径. 典型的高次谐波谱具有以下特征：低阶次谐波的转换效率随着阶次的增加而急速下降，然后出现一个谐波效率几乎不变的平台区域，最后谐波在平台区域末的某一阶次位置处截止. 高次谐波辐射过程可以用半经典三步模型来解释[2]：首先，处在基态的电子通过多光子电离或者隧穿电离进入到连续态；其次，进入连续态的准自由电子在随着外场的振荡过程中而获得额外的能量；最后，电子电离后，先在激光场中加速，然后当激光场反向时，一部分电子在激光场的作用下返回到原子核附近并复合到基态，同时辐射出高能光子. 按照这个模型，光子的最大能量为Ip+3.17Up，其中Ip为原子的电离势，Up为电子的有质动力能. 上述过程在驱动光的每半个光周期内重复一次，因此在时域上表现为一个阿秒脉冲链的形式.

从实用的角度讲，孤立的单阿秒脉冲更有研究价值，所以研究人员主要关注怎样从高次谐波辐射中提取孤立的阿秒脉冲. 目前实验上有两种方法可以实现单个阿秒脉冲：一种方法是周期量级激光泵浦方案[3-5]，另一种方法是偏振态门方案[6，7]. 最近，Gaumnitz等[8]利用双周期的中红外激光实现了脉宽仅为43 as的软X射线脉冲，这是迄今为止实验上所产生的最短阿秒相干光脉冲. 理论上，研究人员提出了多种有效方案来缩短阿秒脉冲的脉宽或者提高阿秒脉冲的强度，如双色场[9，10]、电离门方案[11]、叠加态方案[12，13]、啁啾场[14]、静电组合方案[15]等.

近年来，基于空间非均匀场驱动的等离激元高次谐波的产生引起了研究人员的广泛兴趣. 实验上，空间非均匀场可通过激光脉冲与金属纳米天线、纳米尖及纳米波导等结构的相互作用来产生[16-18]. 由于表面等离激元共振增强被限制在纳米结构单元附近很小的区域内，导致增强电场在纳米量级的空间尺度下具有不均匀性，因此产生的等离激元场为空间非均匀场. 此外，在没有额外激光放大腔体或激光泵浦的条件下，表面等离子共振能够使入射激光强度增加2-3个数量级，这超过了激光在惰性气体中产生高次谐波的阈值强度. 目前，关于等离激元高次谐波的研究工作已被实验和理论报道[19-23]. 与传统均匀场相比，空间非均匀场能够再加速电子，在这个过程中，复合电子经历了更长的谐振时间，从而获得了额外的动能，因此高次谐波谱的截止区会得到极大地延伸. 最近，由空间非均匀场驱动产生的孤立阿秒脉冲引起人们的广泛关注[24-27]. 在本课题组之前的工作中，利用空间非均匀场驱动氦离子获得了脉宽分别为17.3 as和15.2 as的单个阿秒脉冲[28，29].

通过文献调查发现，虽然空间非均匀场、啁啾场与原子或分子系统的高次谐波研究工作已经发表，但目前关于啁啾场结合空间非均匀效应驱动预激发氦离子的高次谐波研究工作却鲜有报道. 另外，在大多数方案中，均采用少周期激光脉冲，相比多周期激光脉冲，少周期激光脉冲不易在实验上实现. 基于上述原因，本文更深地开展了多周期空间非均匀啁啾场驱动预激发氦离子的高次谐波辐射及单个阿秒脉冲的产生. 结果表明：利用空间非均匀啁啾场作为驱动源，不仅能拓展谐波截止，而且能产生频带很宽且只有单一量子路径起主导作用的超连续谱. 叠加连续谱上的一段谐波，直接产生了脉宽仅为11.4 as的单个超短脉冲.通过调节驱动脉冲的持续时间，可获得一个脉宽仅为10 as的单个脉冲. 此外，应用小波时频分布和经典三步模型解释了高次谐波辐射及孤立阿秒脉冲产生的物理机制.

2 理论模型与方法

在长度规范和偶极近似下，原子在激光场中的含时Schrödinger方程可表示为(无特别说明，本文均采用原子单位)：

(1)

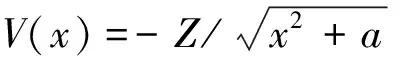
(2)

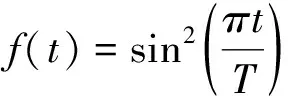
初始态为基态和第一激发态的等权相干叠加态，可表示为：

(3)

其中|g〉、|e〉分别表示基态和第一激发态波函数.

利用二阶分裂算符方法求解方程(1)，可获得体系在任意时刻的波函数ψ(x，t). 在计算中，空间长度为2457.6 a.u.，空间步长为0.15 a.u.，时间步长为0.02 a.u.. 同时，为了避免波函数在边界处发生反射，在每演化完一个时间步之后在波函数上乘以cos1/8的面具函数. 得到波函数后，根据Ehrenfest定理[30]，电子含时偶极加速度a(t)为：

(4)

通过对电子偶极加速a(t)进行傅里叶变换，可获得高次谐波功率谱：

(5)

式中q是谐波阶次.

电子的电离几率随时间的变化关系为：

(6)

上式求和遍及所有束缚态，φn(x)是第n个束缚态的波函数.

通过叠加一些连续谐波，可以获得阿秒脉冲的时域分布：

(7)

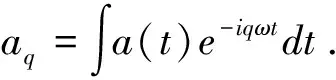
通过小波变换，可获得某一阶次谐波的时频特征，即频率为ω的谐波在t0时刻的振幅为：

(8)

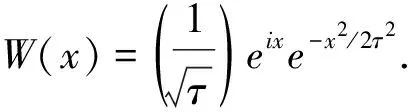
3 结果与讨论

图1给出了初态为He+离子的基态和第一激发态的等权叠加在三种激光场作用下的高次谐波谱. 从图1(a)可知，在单个800 nm的激光场作用下，谱截止位置处于第72阶次谐波，仅仅在截止区的几个谐波是连续的. 在单个啁啾场作用下(β=7.1)，谐波截止扩展到第518阶次谐波，且阶次高于90的谐波是连续的，相对应的连续谱宽度为664 eV. 虽然利用单个啁啾场驱动预激发的氦离子可以获得连续谱，但谐波谱仍然显示强的调制，这不利于单个超短阿秒脉冲的产生. 为了更大地拓展谐波截止，进而拓展连续谱的宽度以及减小谐波啁啾，本文引入一个空间非均匀性参数到啁啾场中，以下称为空间非均匀啁啾场(β=7.1，ε=0.004). 如图1中蓝虚线所示，在空间非均匀啁啾场作用下，谐波截止扩展至第1050阶次，并且在300阶次以上的谐波是连续的，形成一个宽度约为1163 eV的超连续谱. 此外，与以上两种光场作用下得到的谐波谱相比，在空间非均匀啁啾场作用下，谐波谱变得更规整、更光滑. 因为光滑谐波覆盖极其宽的频谱范围，这意味在空间非均匀啁啾场作用下，叠加大范围的连续谐波将会产生一个脉宽超短的单个阿秒脉冲.

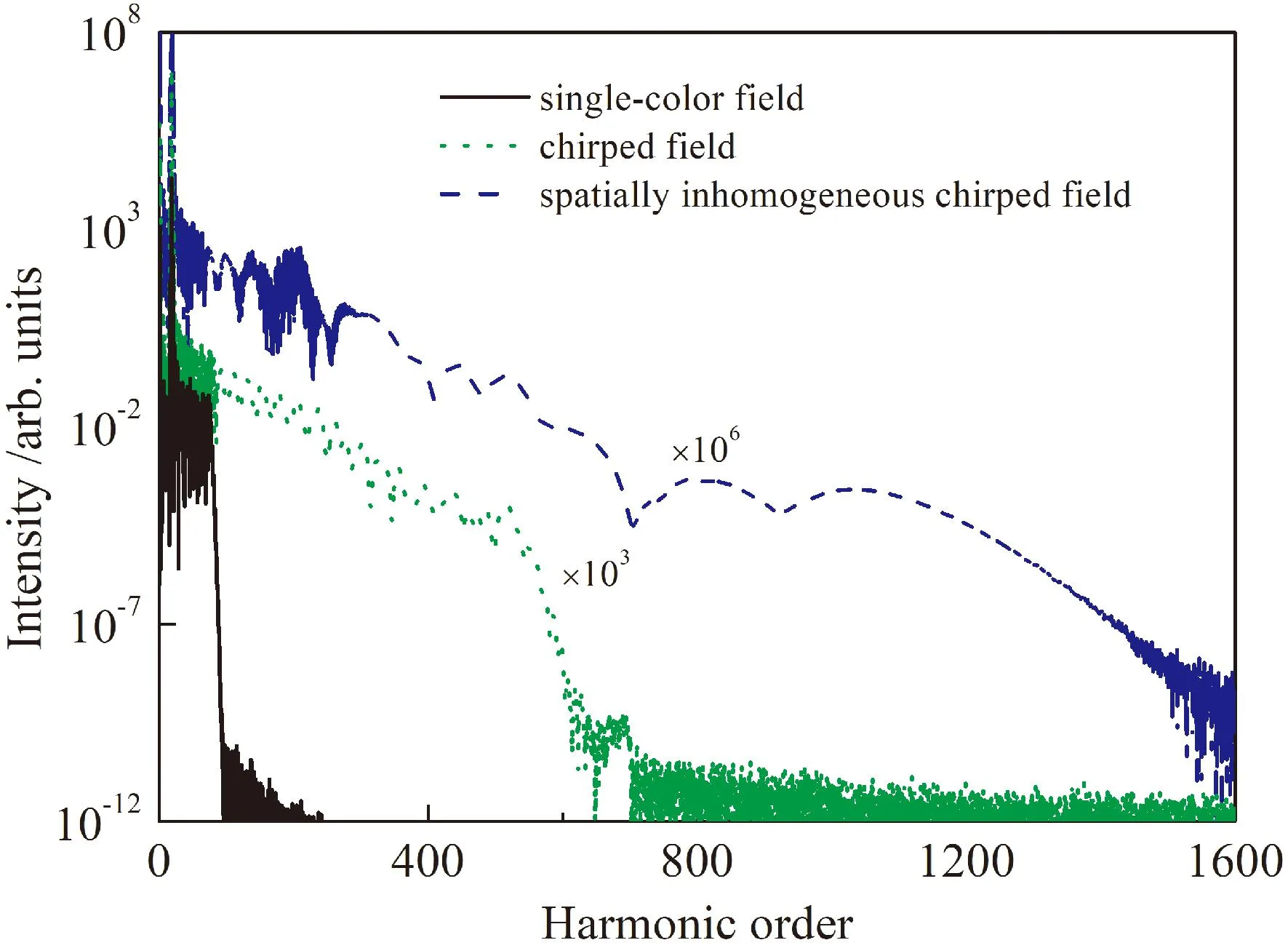
图1 不同激光场作用下He+离子的谐波谱. 黑实线：单色场；绿虚线：啁啾场；蓝虚线：空间非均匀啁啾场. 初态选取为He+离子的基态和第一激发态的等权相干叠加. 驱动脉冲的强度为I=3×1014W/cm2，啁啾参数为β= 7.1、t0= 198 a.u.、τ0= 200 a.u.和非均匀参数是ε=0.004.Fig. 1 Harmonic spectra of the He+ ion driven by three different laser fields. Black solid line：single-color field；green dotted line：chirped field；blue dashed line：spatially inhomogeneous chirped field. The initial state of the He+ ion is prepared as a coherent superposition of the ground state and the first excited state with equally weighted population. The intensity of the driving pulse is I=3×1014W·cm-2，the chirped parameters are set to be β=7.1，t0=198 a.u.，τ0=210 a.u. and the inhomogeneous parameter is ε=0.004.

图2 不同激光场中高次谐波谱的时频分布：(a)啁啾场；(b)空间非均匀啁啾场.Fig. 2 Time-frequency distributions for the HHG spectra in different laser fields：(a)Chirped field. (b)Spatially inhomogeneous chirped field.

通过以上讨论可知，在空间非均匀场驱动下，不仅能够有效扩展谐波谱的截止位置，而且能够产生单一量子路径起主导作用的超连续谱. 而量子路径选取的一个直接应用就是可以产生单个阿秒脉冲. 为了证实该观点，本文对空间非均匀啁啾场中阿秒脉冲的产生情况进行了研究. 作为对比，本文也给出单个啁啾场中阿秒脉冲的生成情况，结果如图3(a)所示. 对于单个啁啾场，通过叠加505-545阶次谐波，在时域上得到了一个脉宽为71 as单个脉冲. 然而这个阿秒脉冲仍然较宽，远大于原子中电子运动的时间尺度(24 as)，其应用将会受到限制. 对于空间非均匀啁啾场，通过滤出连续谱上880-1120阶次谐波，在没有任何相位补偿的情况下，在时域上得到了一个脉宽为11.4 as单个脉冲，这非常接近公式ΔT=T0/N的预测结果[31]. 进一步研究表明：通过叠加连续谱上不同阶次的谐波，可以得到不同脉宽的单个超短阿秒脉冲，如图3(c)和3(d)所示，这为实验上产生中心频率可调谐的单个阿秒脉冲提供了方便.

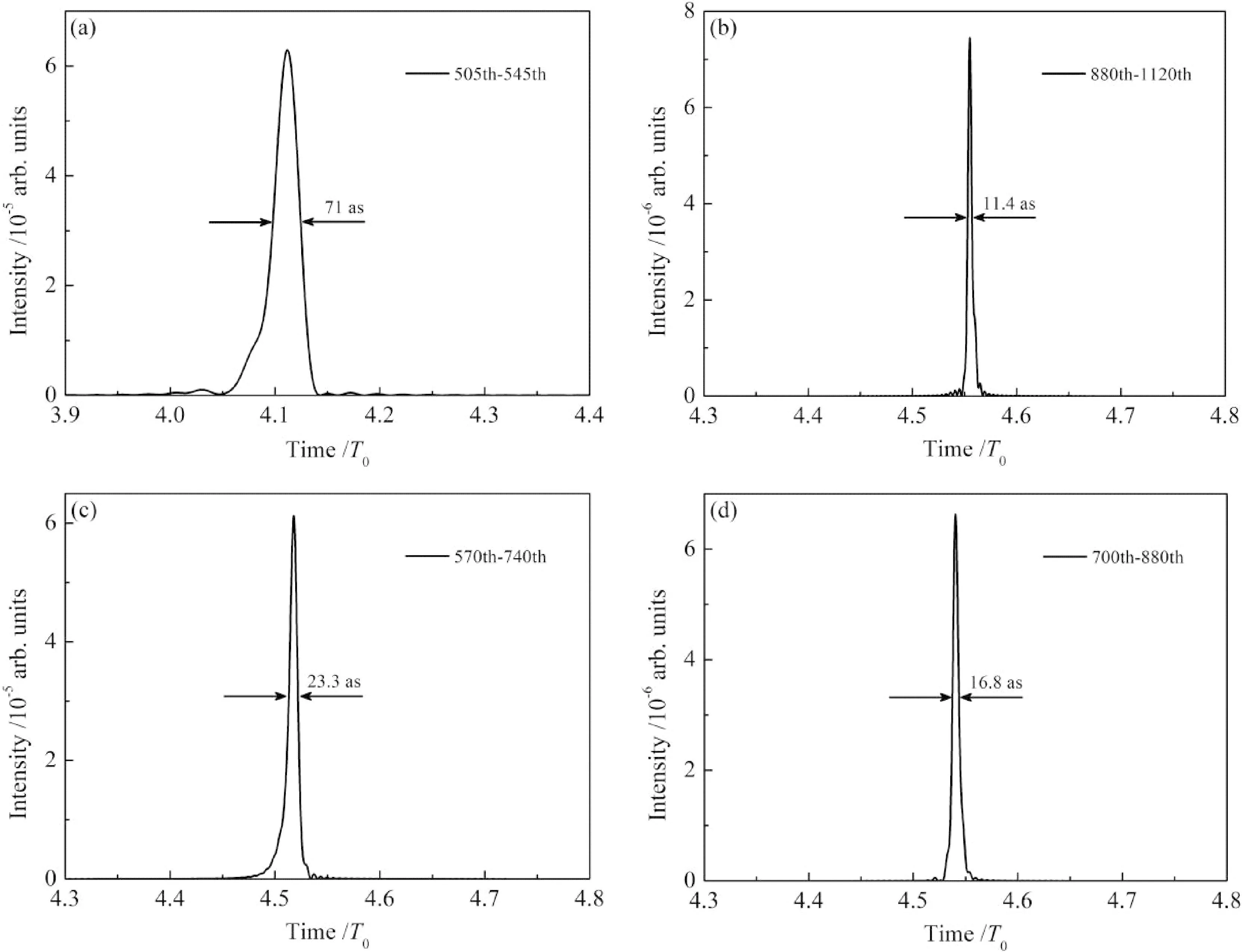
图3 不同激光场中产生的阿秒脉冲：(a)啁啾场中叠加505-545阶次谐波得到的阿秒脉冲时域包络；(b)-(d)空间非均匀啁啾场中叠加不同阶次谐波得到的阿秒脉冲时域包络.Fig. 3 Attosecond pulses generated by different laser fields：(a)Temporal profile of the attosecond pulse by superposing the harmonics from the 505th to 545th order in the chirped field. (b)-(d)Temporal profiles of the attosecond pulses by superposing different order harmonics in the spatially inhomogeneous chirped field.

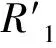
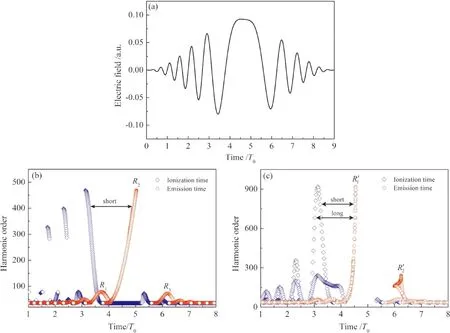
图4 激光脉冲的电场和经典电子轨道示意图：(a)啁啾脉冲的电场；啁啾场(b)和空间非均匀啁啾场(c)中谐波阶次与电离时间和发射时间之间的关系.Fig. 4 Electric field of the laser pulse and the schematic of the classical electron trajectory：(a)Electric field of the chirped pulse. Dependence of the harmonic order on the ionization and emission times in the chirped field (b)and in the spatially inhomogeneous chirped field (c).

图5 脉冲持续时间为19T0的空间非均匀啁啾场中的结果：(a)脉冲持续时间分别为19T0(红虚线)和9T0(蓝实线)的空间非均匀啁啾场驱动得到的谐波谱；(b)驱动脉冲的电场和电离几率随时间的变化关系；(c)对应(a)中红线所示的高次谐波谱的时频分布；(d)叠加880-1120阶次(黑虚线)、1090-1390阶次(红实线)谐波得到阿秒脉冲时域包络.Fig. 5 Results inthe spatially inhomogeneous chirped field with pulse duration of 19T0：(a)Harmonic spectra in the spatially inhomogeneous chirped field with pulse duration of 19T0 (red dotted line)and with pulse duration of 9T0(blue solid line)，respectively. (b)Electric field of the driving pulse and the dependence of the ionization probability on the time. (c)Time-frequency distribution for the HHG spectrum corresponding to the red dotted line in (a). (d)Temporal profiles of the attosecond pulses by superposing the harmonics of the 880th-1120th order (black dotted line)and the 1090th-1390th order (red solid line).

4 结 论

本文提出一种利用多周期空间非均匀啁啾场驱动预激发氦离子来产生高次谐波，进而获得单个短阿脉冲的有效方案. 研究结果表明：当驱动脉冲的脉宽为9 fs时，可使高次谐波的截止扩展至1050阶次，并且产生了只有单一短量子路径贡献的超连续谱，其谱宽为1163 eV.通过对连续谱上不同范围的谐波进行叠加，得到了一系列中心频率可调谐的、脉宽超短的单个阿秒脉冲，其最短脉冲可达11.4 as. 当驱动脉冲的脉宽增加至18.5 fs时，谱截止可以被进一步拓展到1260阶次，同时获得了谱宽达589 eV的高效超连续谱.对该连续谱上1090-1390阶次的谐波进行滤波，直接产生一个脉宽仅为10 as的单个脉冲，这非常接近傅里叶变换极限脉冲. 与9 fs脉冲驱动得到的阿秒脉冲相比，其强度提高了数倍. 总之，本方案的优点在于利用多周期空间非均匀啁啾场实现了高次谐波截止位置的有效拓展，进而获得了频谱很宽且只有单一量子路径贡献的超连续谱，这对实验上产生单个超短阿秒脉冲是非常有利的. 然而，由于连续谱的转换效率仍然较低，产生的阿秒脉冲强度不高. 因此，在本课题组在未来的工作中，从理论上继续探索既能增强谐波效率又能扩展谐波截止的新方案，以便获得更高强度、更短脉宽的孤立阿秒脉冲.