Mo1-xWxC碳化物稳定性及力学性质的第一性原理计算

周少兰, 丛大龙, 杨九州, 李 立, 黄安畏, 冉旭东, 陈汉宾, 李忠盛

(西南技术工程研究所, 重庆 400039)

1 引 言

金属碳化物由于尺寸细小、弥散分布等特性，在钢中起晶粒细化及沉淀强化作用，对钢的力学性能影响显著[1]. 因此，众多学者对碳化物在钢中的固溶析出行为以及在钢中的沉淀强化作用进行了广泛的研究，发现Mo、Zr、Nb、V、W等元素在钢中的合金化中作用突出，并对碳化物的析出影响较大. 合金元素直接影响碳化物的种类和含量，从而影响整个钢铁材料的力学性能，研究表明[2-4]向低碳微合金钢中加入一定量的Mo、W，会形成一种具有“极高热稳定性”的复合碳化物，大幅度提高了钢的强度，因此对这两种合金元素展开了大量研究.

Wang等人[5]等通过透射电镜及三维原子探针等表征手段研究了Mo含量对Nb-Mo-V钢中组织转变及碳化物的影响，研究表明Mo能降低合金元素在碳化物中的扩散速率，从而抑制碳化物粗化. 熊辉辉[6]通过构建离散点阵平面/最近邻断键(DLP/NNBB)模型，并进行第一性原理计算，研究发现Mo固溶进NbC后能降低(Nb、Mo)C与铁素体的界面能，随着Mo含量的升高，Nb-Mo钢中晶粒变细且铁素体中纳米碳化物的析出量增加. Leder mueller等人[7]发现Mo对位错恢复有延缓作用，同时在时效过程中，Mo会分裂成纳米级Nb-C溶质团簇和NbC和Fe3C沉淀，延缓这些相的粗化，从而提高钢的强度. Jang等人[8]通过第一性原理研究Mo、W对Ti-MO钢中TiC碳化物稳定性的影响，研究表明：Mo固溶到TiC中，降低了界面化学能，促进了碳化物的形成. Zhou等人[9]通过第一性原理计算了Mo、W对MC型碳化物的形成能和MC/Fe体系界面能的影响，研究表明：Mo、W进入MC中升高了形成能，但体系界面能降低. Zhao等人[10]通过对钢析出行为研究分析，研究发现：在含有W元素的钢中，析出相均含有W元素，且奥氏体晶粒尺寸和析出相的尺寸均随着W含量的增加而减小. Wen等人[11]对比分析了六种NaCl型过渡金属碳化物MC的稳定性和力学性能，研究表明：NaCl型MoC形成能为正，热力学不稳定. Lin和Deng[12]采用基于局部密度泛函理论的LMTO-ASA方法，结合线弹性理论，从第一性原理出发，计算了具有B1结构的过渡金属WC、MoC、WN和MoN的碳化物和氮化物的剪切模量. Li等人[13]对比分析了三种晶体结构(WC、MoC、NaCl型)中WC的结构稳定性和力学性能，计算得到的零压平衡晶格常数与已有的实验和理论结果吻合较好. 形成焓表明WC型最稳定，其次是MoC型，最后是NaCl型. 根据弹性稳定性准则，预测三种结构均为机械稳定结构，并研究了三种结构在0-100 GPa压力范围内的弹性常数、弹性模量等参数. 综上所述，目前对碳化物析出及其界面行为研究较多，关于Mo、W对碳化物的结构与力学性质影响的定量研究较少.

本文通过虚拟晶体近似构建不同掺杂含量的Mo1-xWxC模型，采用第一性原理方法计算了Mo1-xWxC碳化物的结合能、形成能、弹性常数、弹性模量、硬度、韧脆性等力学参数，判断Mo1-xWxC的稳定性，研究Mo1-xWxC碳化物的力学性能变化规律，为新型钢铁材料的设计提供基础数据.

2 计算方法与模型

本文研究主要在Materials Studio软件中的CASTEP模块中进行，整个计算采用周期性边界条件对模型简化处理[14]. 在进行计算前，对参数进行了收敛性测试，测试后截断能为400 eV，K点取18×18×18，体系自洽迭代能量差收敛值取10-5eV/atom，交互关联函数采用Perdew-Burke-Ernzerho(PBE)框架下的广义梯度近似. 同时在保证计算精度的同时，为了提高计算时间，采用Pulay密度混合法加速自洽循环，最后采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)方法对晶胞进行结构优化.

本次研究主要以具有简单六方点阵结构的MoC为研究对象，通过虚拟晶体近似构建不同W含量的Mo1-xWxC碳化物模型. 虚拟晶体近似方法允许两种以上元素占据同一个原子，该方法已被证实可应用于部分合金相及固溶体的计算研究中[15].

3 结果与讨论

3.1 晶格常数

在进行碳化物力学性质计算前，需要对模型进行结构优化. 优化后的晶格常数结果列于表1，由表1可见，本次计算值与实验数据以及其他计算方法获得的结果均符合较好，误差小于1%，表明此次计算方法与模型是较为合理可靠的，在此基础进行其余性质计算.

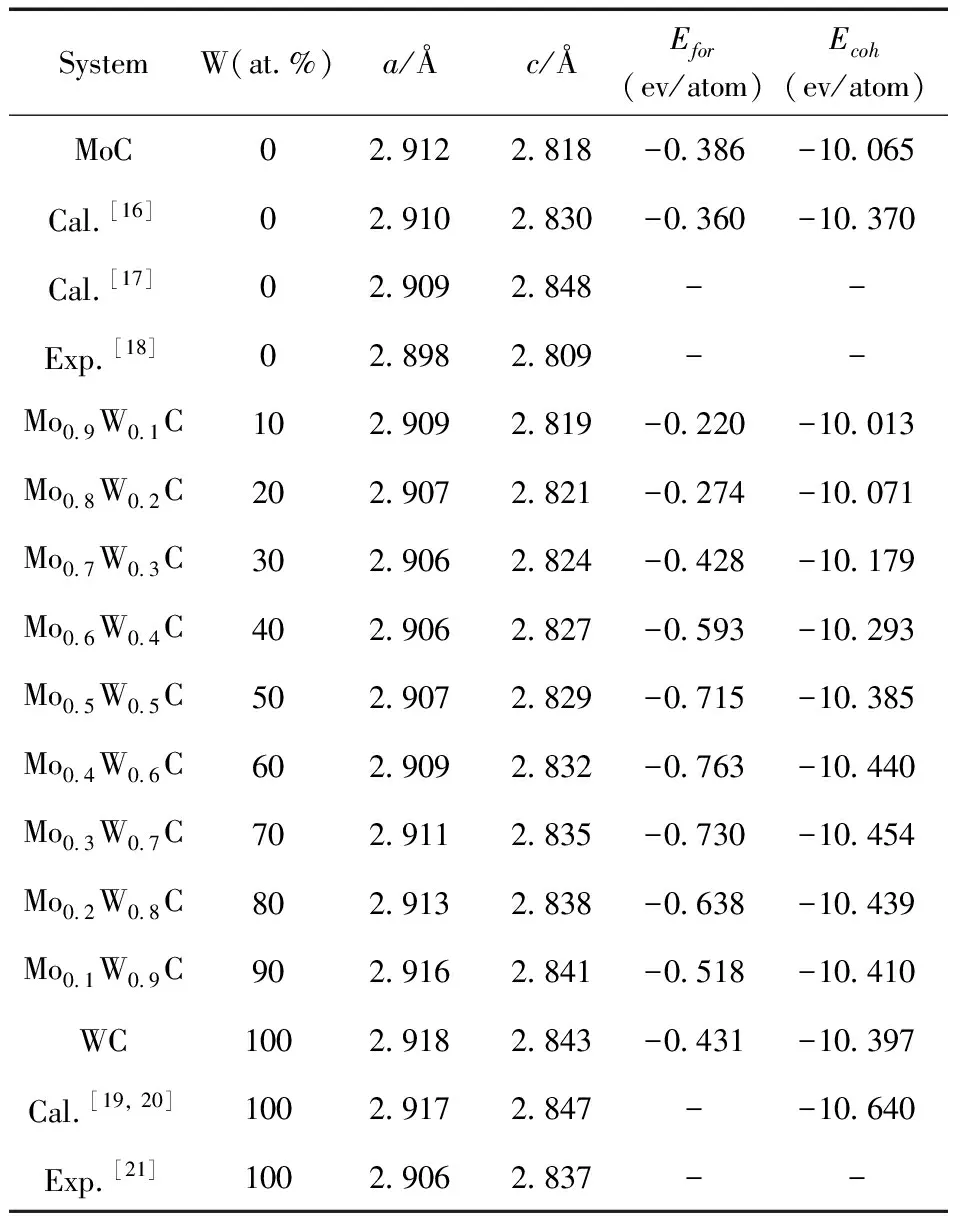
表1 Mo1-xWxC的晶格常数、形成能、结合能

图1为Mo1-xWxC碳化物的晶格常数与W含量的关系，从图中可以看出：随着W含量的增加，晶格常数a先降低加后增加，晶格常数c呈线性增加.

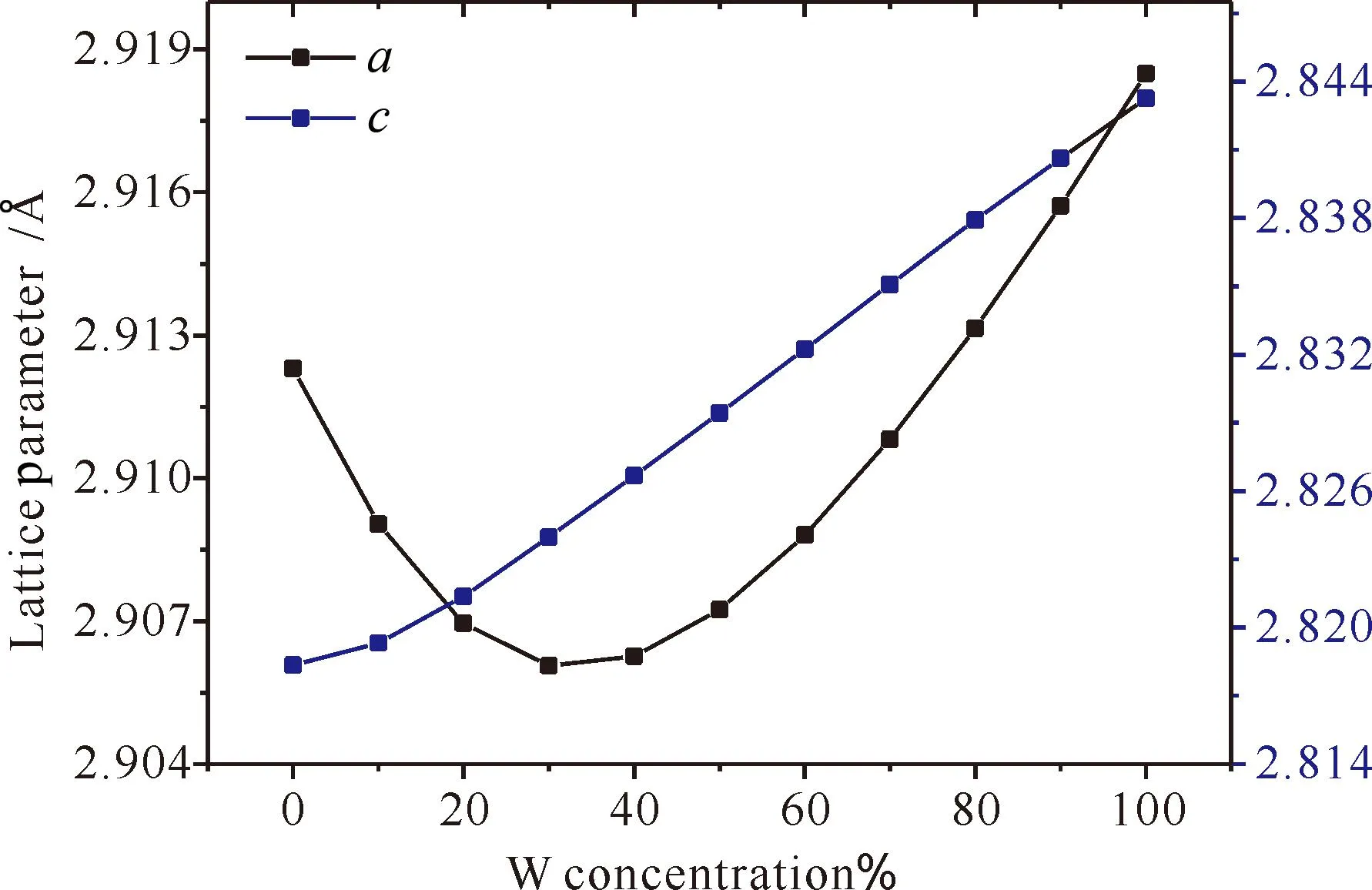
图1 Mo1-xWxC 的晶格常数Fig. 1 Lattice parameters of Mo1-xWxC

3.2 形成能与结合能

碳化物的稳定性对材料的力学性能影响很大. 为了研究Mo1-xWxC稳定性，我们计算了不同掺杂含量下Mo1-xWxC的形成能、结合能. 形成能表示原子从单质态形成碳化物过程中释放(或吸收)的能量，结合能表示n个孤立且自由的原子紧密粘合在一起所需的能量.以MoC为例，形成能、结合能计算公式为：

(1)

(2)

通过公式计算的不同掺杂含量下Mo1-xWxC的的形成能、结合能如表1所示，本次计算的MoC的形成能、结合能是-0.386 eV/atom、-10.065 eV/atom，与文献[16，19，20]中的计算值及实验值偏差较小，表明本次计算结果是合理可靠的，负的形成能表明体系在热力学上是自发形成的，结合能表示组成晶体的原子在其晶体状态与自由原子状态之间变化的能量差值. 形成能为负值，说明该体系能自发形成，值越负表明该体系形成越容易；结合能为负值，说明晶体可稳定存在，其数值越负，说明晶体结构越稳定.

如图2所示，在MoC中掺入W时，结合能、形成能均为负值，表明Mo1-xWxC能自发形成且能稳定存在. 随着W含量的增加，形成能呈倒U字形变化趋势，当W含量为0.6时，形成能绝对值最大，这表明Mo0.4W0.6C是最容易形成的，同时随着W含量的增加，结合能绝对值增加，表明Mo1-xWxC稳定性随着W含量的增加而增加.

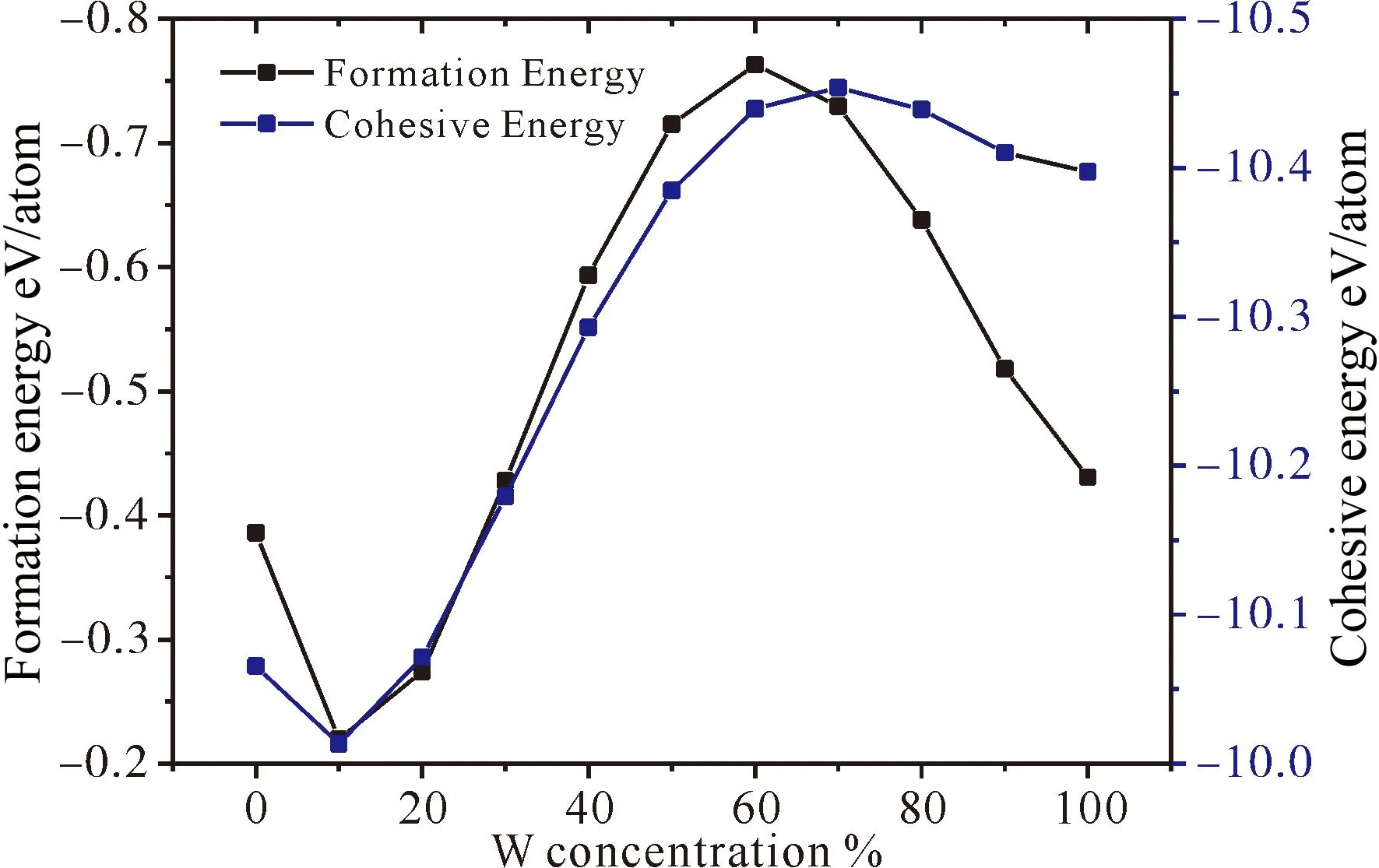
图2 Mo1-xWxC的形成能与结合能Fig. 2 Formation energy and cohesive energy of Mo1-xWxC

3.3 力学性质

3.3.1弹性性质

本次计算的Mo1-xWxC碳化物为密排六方结构，在Castep计算中可以直接得到5个独立弹性常数C11、C12、C13、C33、C44. 基于Viogt-Reuss近似[22]，体积模量、剪切模量等计算公式为：

(3)

(4)

(5)

(6)

依据Hill近似[23]，Hill体模量以及剪切模量定义为Voigt和Reuuss值的平均值BH=1/2(BV+BR)和GH=1/2(GV+GR). 对多晶体而言，杨氏模量的计算公式为：

(5)

晶体的力学稳定性可以借助于独立弹性常数进行判定，六方晶系相结构的Born力学稳定性判据[24]为：C11-C12>0，(C11-C12)C33-2C132>0，C44>0.

表2列出了不同W含量的Mo1-xWxC弹性常数，从表中可以看出：不同掺杂含量下的Mo1-xWxC均满足Born判据，在力学上是稳定的，为了更清楚的显示Mo1-xWxC弹性常数的变化，将结果绘于图3，从图中可以看出：随着W含量的增加，弹性常数C11、C33、C44线性增加，C11、C33、C44分别反映a、c方向的抗压缩能力和a方向的抗剪切变形的能力，计算结果表明Mo1-xWxC碳化物的抗压缩和抗剪切变形能力均随着W含量的增加而增加.

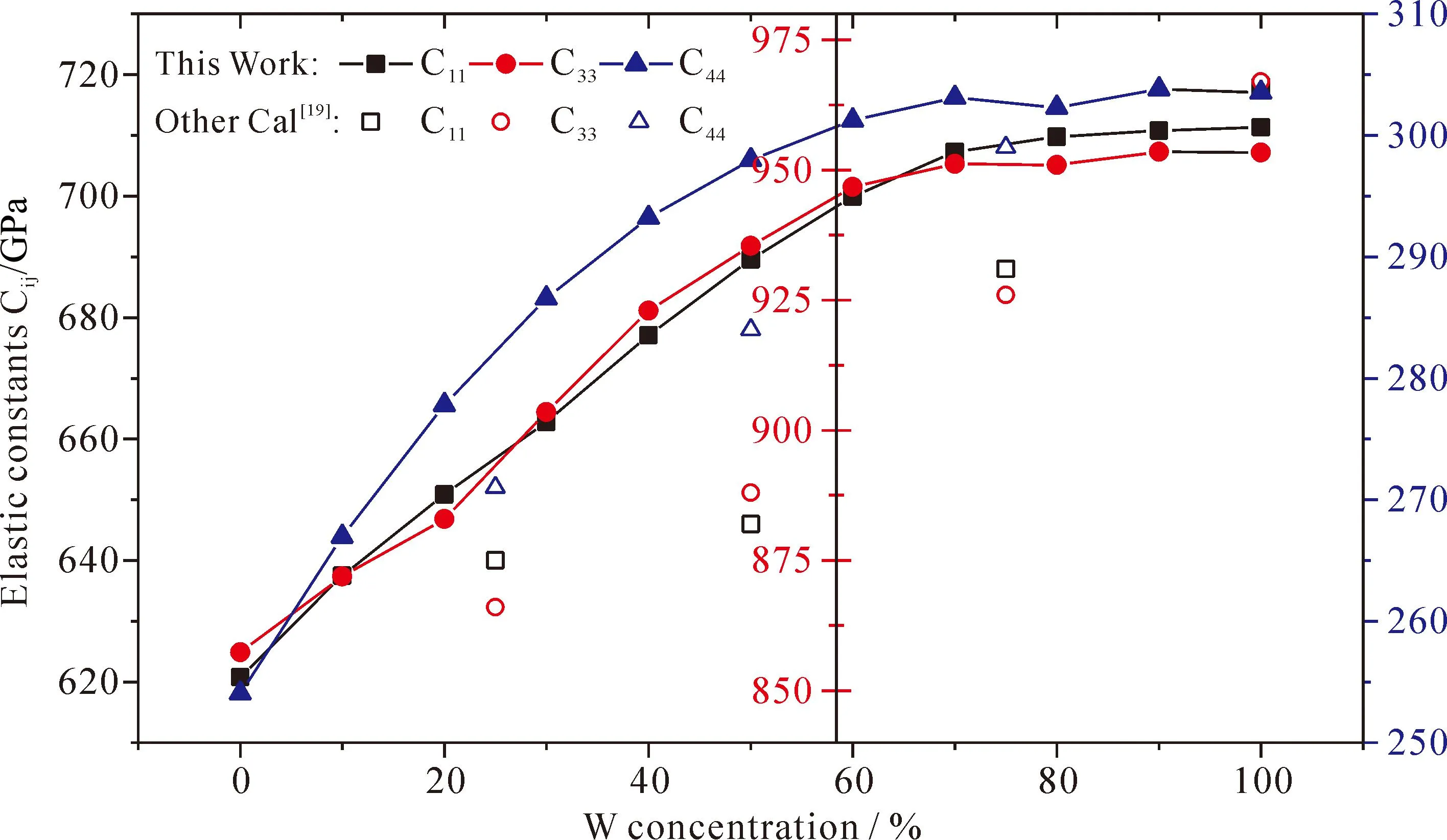
图3 Mo1-xWxC的弹性常数Fig. 3 Elastic constants of Mo1-xWxC

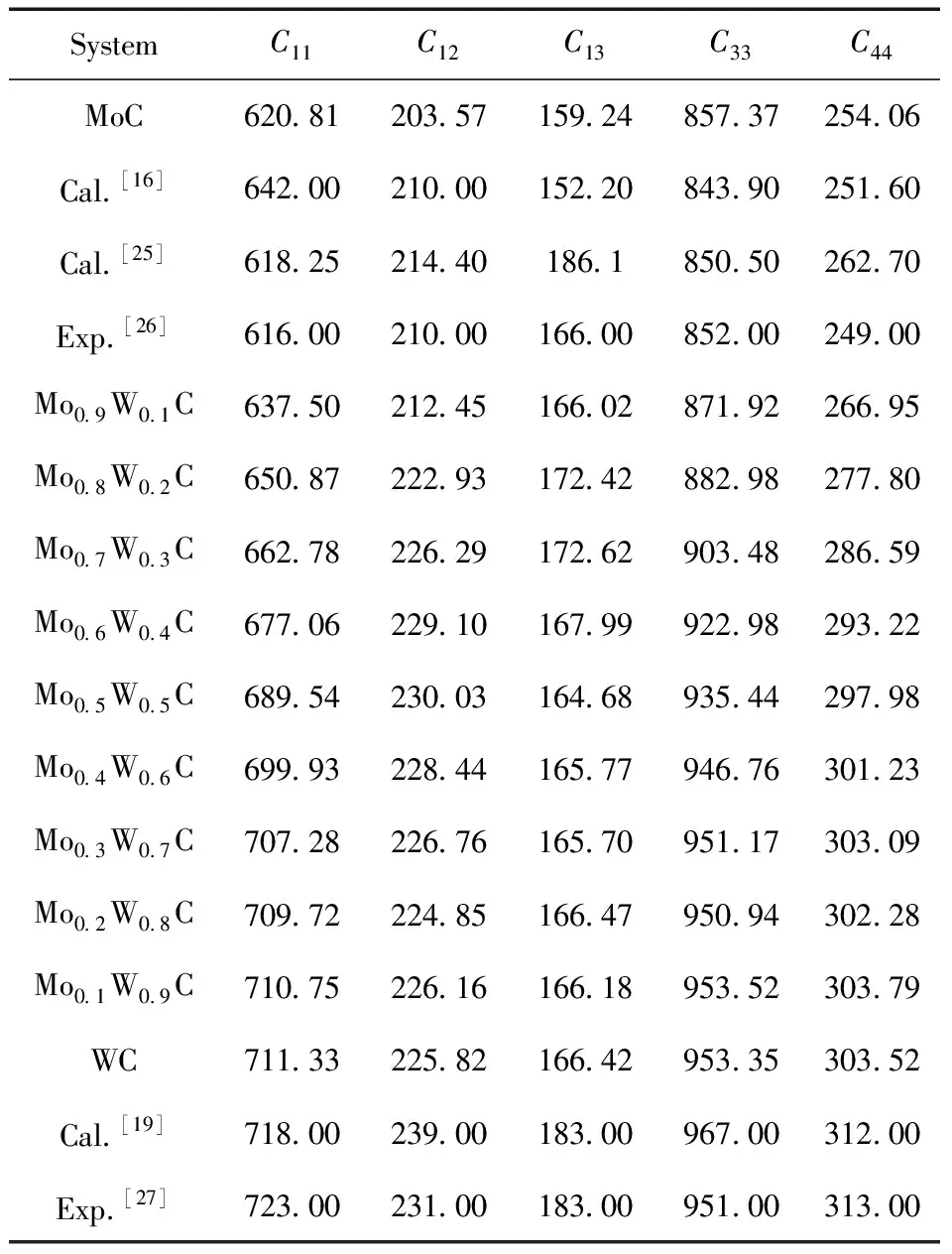
表2 Mo1-xWxC的弹性常数 (单位：GPa)

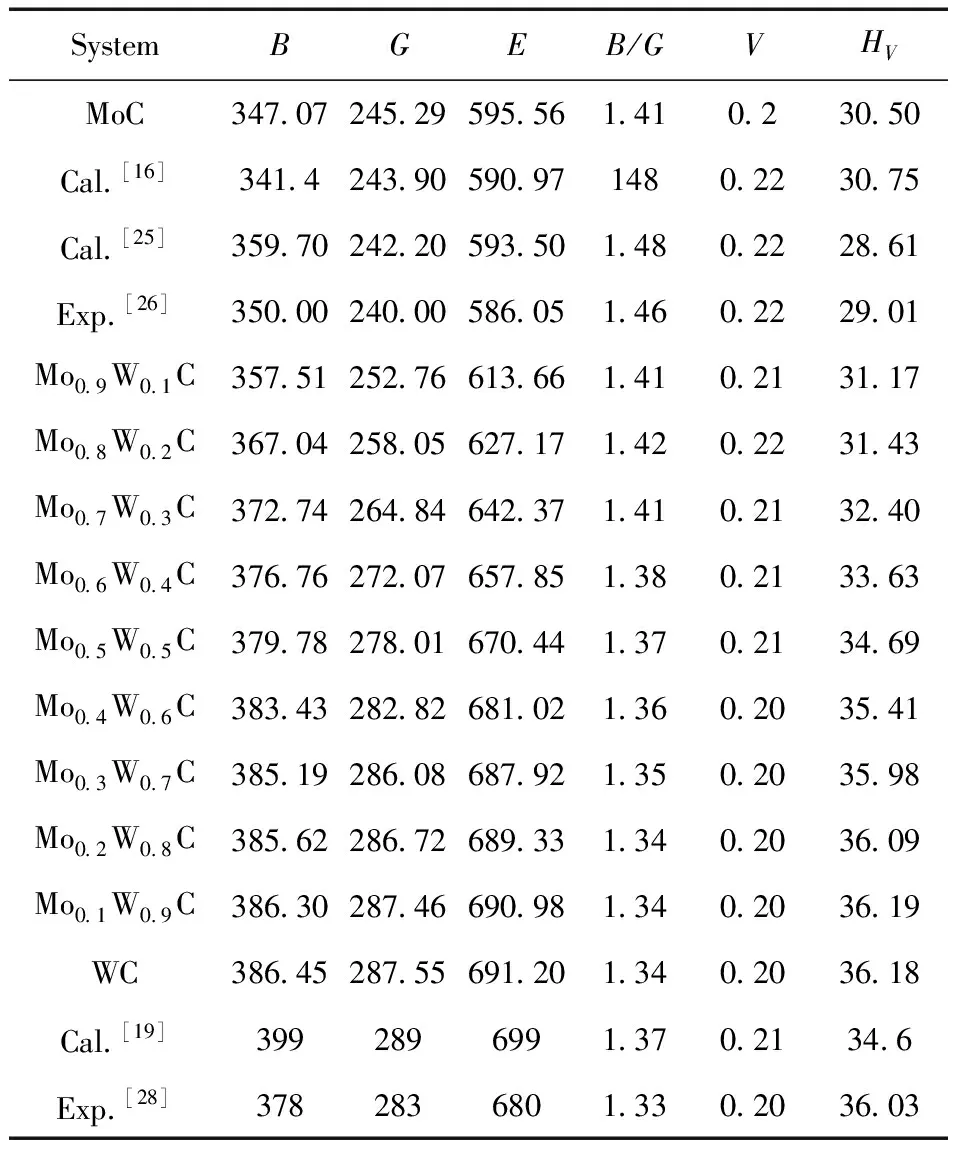
表3 Mo1-xWxC的弹性模量 (单位：GPa)

图4为Mo1-xWx碳化物的体模量(B)、剪切模量(G)、杨氏模量(E)，图4表明：随着W含量的增加，Mo1-xWx碳化物的三种弹性模量均增加. 体模量、剪切模量可以分别表示材料对体积和形状变化的抵抗力，值越大，抵抗能力越强，相同掺杂含量下，Mo1-xWxC的体模量大于剪切模量，表明受外界力时，Mo1-xWx碳化物倾向于形状变化而不是体积变化. 而杨氏模量为纵向弹性模量，表征材料的抗变形能力，杨氏模量值越大，表示材料的刚度越大. 本次计算结果表明Mo1-xWxC为硬质材料，随着W含量的增加，Mo1-xWx碳化物抗压缩、抗剪切变形能力均增强，且越来越难发生弹性变形.

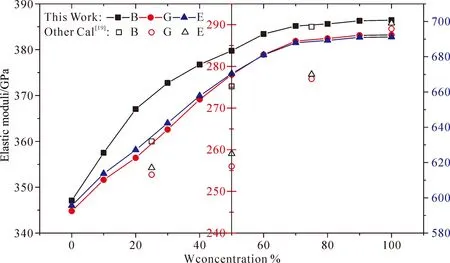
图4 Mo1-xWxC的弹性模量Fig. 4 Elastic moduli of Mo1-xWxC

3.3.2硬度及韧脆性

基于Pugh[29]的经验关系，体模量B与剪切模量G的比值可判断材料的韧脆性行为，当B/G>1.75时，材料呈韧性，反之呈脆性. 此外，泊松比u反映了晶体抗剪切的稳定性，也可以判断材料的本征韧脆性，如果u大于0.26，则材料表现出相对的韧性；否则，材料是脆性的. 图5为本次计算的Mo1-xWxC的B/G与u，两条曲线变化一致，从图中可以看出：Mo1-xWxC碳化物整体呈脆性，随着W含量的增加，Mo1-xWxC脆性增加.

图5 Mo1-xWxC的B/G、泊松比Fig. 5 B/G and Poisson’s ration of Mo1-xWxC

材料的硬度一定程度上表征了材料抵抗变形或断裂的能力，在钢中MoC碳化物是抗磨损相，因此研究这些碳化物是很有必要的，根据Tian等人[30]的理论，材料的硬度可以通过剪切模量等公式推导，计算公式为：

HV=0.92K1.137G0.708

(6)

K=G/B

(7)

耐磨性是极端环境下材料的重要指标，根据Leyland和Matthews所提出的标准，弹性破坏应变HV/E可用来表征合金的耐磨性，图6为Mo1-xWxC碳化物的硬度值及HV/随W含量的变化图，从图中可以看出：随着W含量的增加，Mo1-xWxC维氏硬度和耐磨性皆增加.

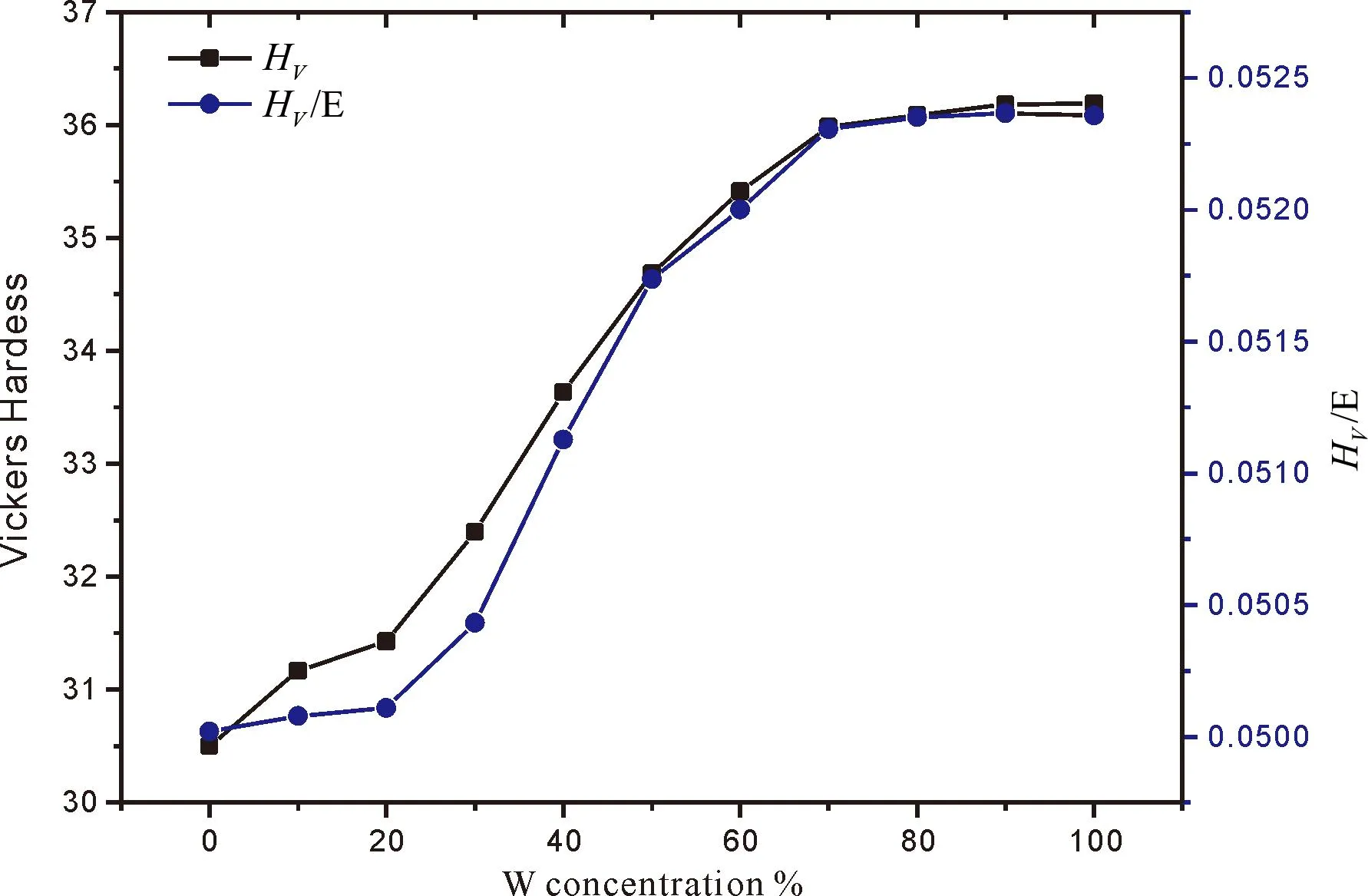
图 6 Mo1-xWxC的硬度及HV/EFig. 6 Vickers hardness and HV/E ratios of of Mo1-xWxC

3.3.3力学各向异性

力学各向异性指数可以定量判断材料的各向异性，进而研究材料在不同方向的力学性质，在材料科学研究中具有重要的应用价值. 而力学各向异性图可以定性判断材料的各向异性，对于各向同性的材料，其三维曲面图为圆球形，各向异性越大，曲面图越偏离球形. Mo1-xWxC碳化物的三维杨氏模量如图7所示，Mo1-xWxC的三维杨氏模量图整体变化不大，随着W含量的增加，Mo1-xWxC的三维杨氏模量趋向于球形，表明Mo1-xWxC呈各向同性，且在MoC中加入W可以降低材料的各向异性.

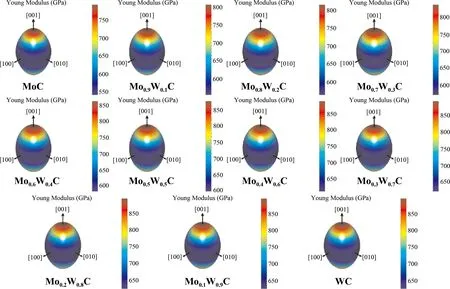
图 7 Mo1-xWxC的三维杨氏模量图7 3D visualizations of Young modulus of Mo1-xWxC

3.4 电子态密度

弹性模量反映了晶体中原子间结合力的强弱，为了进一步理解Mo1-xWxC中合金元素之间的成键关系，计算了不同掺杂含量下的Mo1-xWxC的态密度，如图8所示，从图中可以看出：不同掺杂含量下的Mo1-xWxC的总态密度分布趋势基本一致，且在费米能级处的电子态密度值均不为零，说明Mo1-xWxC均具有金属特性并且导电. 同时在费米能级两侧均有明显的尖峰，表明赝能隙的存在，赝能隙可以直接反映该体系成键共价性的强弱，从图中可知，在Mo1-xWxC中，赝能隙的宽度随着W含量的增加而增加，赝能隙越宽，表明该体系成键的共价性越强. 费米能级处的DOS值越低，体系越稳定，Mo1-xWxC在费米能级处的DOS值分别为0.47、0.41、0.35、0.30、0.27、0.25、0.24、0.24、0.24、0.23、0.23，表明随着W含量的增加，Mo1-xWxC碳化物的稳定性逐渐增强.

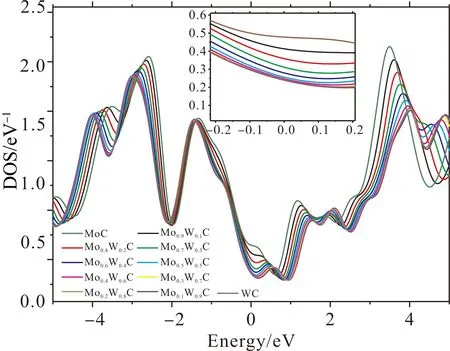
图 8 Mo1-xWxC的态密度Fig. 8 Density of states of Mo1-xWxC

4 结 论

本文通过第一性原理结合虚拟晶体近似方法系统研究了不同掺杂含量下Mo1-xWxC碳化物的稳定性、力学性质和电子性质，研究表明：Mo1-xWxC能自发形成且稳定存在，随着W含量的增加，Mo1-xWxC的稳定性、体模量、杨氏模量、剪切模量、维氏硬度、耐磨性均增加，而W的添加会导致材料脆化，同时Mo1-xWxC碳化物的脆性随着W含量的增加而增加.