连续分布电荷体系电荷元的自能问题*
付全红 常 健 郑建邦
(西北工业大学物理科学与技术学院 陕西 西安 710129)
电荷体系的能量是一个被广泛讨论的问题.当一个电荷体系由若干部分组成时,电荷体系的电场能等于各部分的自能与各部分之间的相互作用能之和.一个连续分布电荷体系,例如连续带电体、连续带电曲面等,可分割为无穷多个电荷元,电荷体系的电场能等于电荷元的自能与电荷元之间的相互作用能之和[1-4].文献一般认为,由于电荷元的电荷量趋于零,故电荷元的自能趋于零,所有电荷元的自能之和也趋于零,因此,电荷体系的电场能就等于电荷元之间的相互作用能[5-10].
上述推理虽然结论正确,但是不够严谨,原因在于虽然电荷元的自能趋于零,但是电荷元的数目趋于无穷大,因此,所有电荷元的自能之和也趋于零需要从数学上严格证明.文献[11-12]以自由体电荷为例对该问题做了一些研究,但是没有涉及面电荷和极化电荷的情形.
本文系统研究连续分布电荷体系电荷元的自能问题,利用均匀带电球体和均匀带电圆面的自能公式和夹逼定理,分两步严格证明连续分布电荷体系电荷元的自能之和为零:第一步,证明自由电荷体系电荷元的自能之和为零;第二步,证明一般电荷体系电荷元的自能之和为零.
1 自由电荷体系电荷元的自能
1.1 自由体电荷的电荷元的自能
考察任意一个自由体电荷,相对介电常数为1,体电荷密度为ρf,体积为V.将自由体电荷分割为N1(N1→∞) 个正方体电荷元,边长为a1(a1→0).
自由体电荷的电场能为[13]
(1)
式中,Ei和Ej分别表示第i个和第j个正方体电荷元在空间产生的电场强度.
第i个正方体电荷元的自能为
(2)
所有正方体电荷元的自能之和为
(3)

(4)

图1 正方体电荷元的内切球和外接球
式中,Qf、R、ρf分别表示均匀带电球体的电荷量、半径、体电荷密度.
为了方便起见,将正方体电荷元减去内切球剩下的部分,或外接球减去正方体电荷元剩下的部分叫做“边角料”.对于图1(a),正方体电荷元的自能等于内切球的自能、“边角料”的自能、内切球与“边角料”的相互作用能之和,由于内切球和“边角料”带同种电荷,相互作用能大于零,故正方体电荷元的自能大于内切球的自能.同理,对于图1(b),正方体电荷元的自能小于外接球的自能.因此
W内切球,i (5) (6) 根据式 (4),内切球和外接球的自能分别为 (7) (8) 式中,ρf,i表示第i个正方体电荷元的体电荷密度. 当a1→0时,W内切球,i→0,W外接球,i→0,根据夹逼定理 W正方体,i→0 (9) 即正方体电荷元的自能为零. 下面证明所有正方体电荷元的自能之和也为零. (10) (11) 式中,|ρf|min和|ρf|max分别表示体电荷密度绝对值的最小值和最大值.由式(6)、式(10)、式(11)得 (12) 当a1→0时,有 根据夹逼定理 (13) 即所有正方体电荷元的自能之和也为零. 考察任意一个自由面电荷,相对介电常数为1,面电荷密度为σf,面积为S.将自由面电荷分割为N2(N2→∞) 个等边三角形电荷元,边长为a2(a2→0). 自由面电荷的电场能为[13] (14) 式中,Ei和Ej分别表示第i个和第j个等边三角形电荷元在空间产生的电场强度. 第i个等边三角形电荷元的自能为 (15) 所有等边三角形电荷元的自能之和为 (16) (17) 图2 等边三角形电荷元的内切圆和外接圆 式中,γ≈1.7为均匀带电圆面的自能系数,Qf、R、σf分别表示均匀带电圆面的电荷量、半径、面电荷密度. 为了方便起见,将等边三角形电荷元减去内切圆剩下的部分,或外接圆减去等边三角形电荷元剩下的部分叫做“边角料”.对于图2(a),等边三角形电荷元的自能等于内切圆的自能、“边角料”的自能、内切圆与“边角料”的相互作用能之和,由于内切圆和“边角料”带同种电荷,相互作用能大于零,故等边三角形电荷元的自能大于内切圆的自能.同理,对于图2(b),等边三角形电荷元的自能小于外接圆的自能.因此 W内切圆,i (18) (19) 根据式(16),内切圆和外接圆的自能分别为 (20) (21) 式中,σf,i表示第i个等边三角形电荷元的面电荷密度. 当a2→0时,W内切圆,i→0,W外接圆,i→0,根据夹逼定理 W等边三角形,i→0 (22) 即等边三角形电荷元的自能为零. 下面证明所有等边三角形电荷元的自能之和也为零. (23) (24) 式中,|σf|min和|σf|max分别表示面电荷密度绝对值的最小值和最大值.由式(19)、式(23)、式(24)得 (25) 当a2→0时,有 根据夹逼定理 (26) 即所有等边三角形电荷元的自能之和也为零. 第1节研究了自由电荷体系电荷元的自能,本节在此基础上研究一般电荷体系 (既有自由电荷,也有极化电荷) 的电荷元的自能.考察任意一个一般电荷体系,介电常数为ε,自由体电荷密度为ρf、自由面电荷密度为σf、极化体电荷密度为ρp、极化面电荷密度为σp.将体电荷分割为N1(N1→∞) 个正方体电荷元,边长为a1(a1→0),面电荷分割为N2(N2→∞) 个等边三角形电荷元,边长为a2(a2→0). 一般电荷体系的电场能为[13] (27) 式中,Ei和Ej分别表示第i个和第j个 (正方体或等边三角形) 电荷元在空间产生的电场强度. 第i个 (正方体或等边三角形) 电荷元的自能为 (28) 所有 (正方体或等边三角形) 电荷元的自能之和为 (29) 先证明一般电荷体系 (正方体或等边三角形) 电荷元的自能为零. (30) (31) 式中,εmin和εmax分别表示介电常数的最小值和最大值.由式(30)和式(31)得 (32) 根据夹逼定理 (33) 即一般电荷体系(正方体或等边三角形) 电荷元的自能为零. 再证明一般电荷体系所有 (正方体或等边三角形) 电荷元的自能之和也为零. (34) (35) 由式(34)和式(35)得 (36) 根据夹逼定理 (37) 即一般电荷体系所有 (正方体或等边三角形) 电荷元的自能之和也为零. 本文系统研究了连续分布电荷体系电荷元的自能问题,利用均匀带电球体和均匀带电圆面的自能公式和夹逼定理,严格证明了连续分布电荷体系电荷元的自能之和为零.因此,连续分布电荷体系的电场能就等于电荷元之间的相互作用能.1.2 自由面电荷电荷元的自能
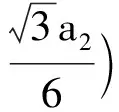

2 一般电荷体系电荷元的自能


3 结论

