关于曲线拐点的一些探讨

刘合财

(贵阳学院 理学院,贵州 贵阳 550005)

拐点是函数性质研究的重要内容,在导数和微分的应用中有重要的地位和作用,反映了平面曲线的内在几何特征,是函数曲线上单调性相同而凸凹性不同的分界点。多篇文献对拐点进行了研究和探讨,一些教材对拐点的定义较宽泛,而有些文献对拐点的定义更严密、更严格。一定程度上对拐点的性质、判定等问题研究不翔实、不系统、不深入。拐点是函数曲线的凸凹性分界点,在Logistic模型中的S型曲线拐点是一个比较特殊的点,在疫情趋势预测、网络舆情预测中也是研究者非常关注的一个重要节点,[1-5]这使得拐点的相关研究具有重要的意义。本文对曲线拐点的定义、性质、判别、计算、应用有一定的探讨和思考。

1 拐点的定义

数学教材中关于拐点有不同的定义,通常定义有：

定义1：若函数y=f(x)在点x0可导,且在点x0的一侧是凸,而另一侧是凹,则称点M(x0,f(x0))是曲线y=f(x)的拐点。[5]

定义2：如果在点x0两侧邻近的曲线y=f(x)具有不同的凸性,则称曲线上的点(x0,f(x0))为曲线y=f(x)的拐点(或变曲点)。[6]

定义3：设曲线y=f(x)在点(x0,f(x0))处有穿过曲线的切线,且在切点近旁,曲线在切线的两侧分别是严格凸和严格凹的,这时称点(x0,f(x0))为曲线y=f(x)的拐点。[7]

按此定义,拐点不仅是凸和凹曲线的分界点,而且必须是曲线的连续点。即拐点是连续曲线上凸凹弧的分界点。

另外,有教材的定义是：光滑曲线上凸凹弧的分界点。连续函数的尖点不光滑,不是拐点。[8]

2 拐点的性质

性质1(必要条件)：若函数曲线y=f(x)以(x0,f(x0))为拐点,且存在f′′(x0),则f′′(x0)=0。

即：函数在其曲线拐点二阶可导,则函数在该点的二阶导数为0。

亦即：函数在其曲线拐点二阶可导的必要条件是函数在该点的二阶导数为0。

性质2(必要条件)：若函数f(x)在(x0-δ,x0+δ)存在连续二阶导数,且以(x0,f(x0))为拐点,则f′′(x0)=0。

即：函数在拐点的一邻域内存在连续二阶导数,则函数在该点的二阶导数为0。

亦即：函数在拐点的一邻域内存在连续二阶导数的必要条件是函数在该点的二阶导数为0。

注1：若已知有f′′(x0)=0,(x0,f(x0))不一定是曲线y=f(x)的拐点。

即：函数在一点的二阶导数为0不是该点为曲线拐点的充分条件。

如：f(x)=x4,f′′(0)=0,(0,0)不是该曲线的拐点。事实上,∀x≠0,f′′(x)>0,f(x)在(0,0)的两侧皆是凸。

注2：若(x0,f(x0))是曲线y=f(x)的拐点,y=f(x)在x0的导数不一定存在。

即：函数在一点的导数存在不是该点为曲线拐点的必要条件。

注3：与极值点的不重合性。函数在拐点处没有极值,即拐点与极值点不能在同一处取到。[9]文献[8]在“光滑曲线上凸凹弧的分界点称为该曲线的拐点”定义下证明了“函数的极值点不可能与拐点重合”,证明了函数曲线的拐点与其极值点的不重合性。

注4：与极值点的关联性。从拐点定义知,若f(x)具有二阶导数,则曲线f(x)的拐点即为f′(x)的极值点。根据f′(x)的极值点的结果就可得到f(x)拐点的相应结果。

3 拐点的判别

因为曲线f(x)拐点与f′(x)极值点的关联性,故可以根据函数f′(x)在一点的高阶导数的符号来判定f′(x)的极值点,从而判定f(x)的拐点。从而有以下结论：

判别2(充分条件)：设f(x)在U(x0,δ)二阶可导,f′′(x0)=0,f′′′(x0)≠0,则(x0,f(x0))是拐点。

判别3(充分条件)：设f(x)在x0的某一邻域内有直到n阶的导数,且f(n)(x)在x0连续,f′′(x0)=f′′′(x0)=…=f(n-1)(x0)=0。而f(n)(x0)≠0,则当n为奇数时(x0,f(x0))是拐点。

这是根据函数极值点的判定定理,当n(≥3)为奇数时,n-1为偶数,[f′(x0)](n-1)=f(n)(x0)≠0,从而f′(x)在x0取极值,(x0,f(x0))是拐点。

此判别法亦可表述为：

设f(x)在x0的某一邻域内有直到2k+1阶的导数,且f(2k+1)(x)在x0连续,f′′(x0)=f′′′(x0)=…=f(2k)(x0)=0,而f(2k+1)(x0)≠0,则(x0,f(x0))是拐点。

在上述判别法的条件中,当n为偶数时,(x0,f(x0))不是拐点。这是因为当n(>3)为偶数时,n-1为奇数,[f′(x0)](n-1)=f(n)(x0)≠0,从而f′(x)在x0不取极值,(x0,f(x0))不是拐点。

4 拐点的计算

根据拐点的定义和判别,拐点左右两侧邻近f′′(x)的符号相异,拐点的计算重点在于找出二阶导数等于0和不存在的点。先找出可能的拐点,当点左右两侧邻域的二阶导数符号相同时该点不是拐点,当符号相反时该点就是拐点。

证：首先求出曲线的三个拐点,

例2：问a和b为何值时,点(1,3)为曲线y=ax3+bx2的拐点?

解：因(1,3)在曲线上,故有a+b=3。

又(1,3)为拐点,且y''=6ax+2b,故y''(1)=6a+2b=0。

5 拐点的应用

拐点除了用于函数图像描绘外还有广泛的应用,在人口预报、疫情预测以及金融学中股票和期货分析等方面以及材料力学、流体力学、机械工程、土木工程、信号处理等工程领域都有广泛而深入的应用。

在疫情预测中,人们非常关注拐点这样一个特殊的节点,其代表了某一指标变化率的一种改变。文献[10]根据有关统计数据画出了COVID-19全国累计报告确诊病例数变化趋势图,进一步研究可以考虑基于统计发布数据的疫情拐点判断等相关问题。

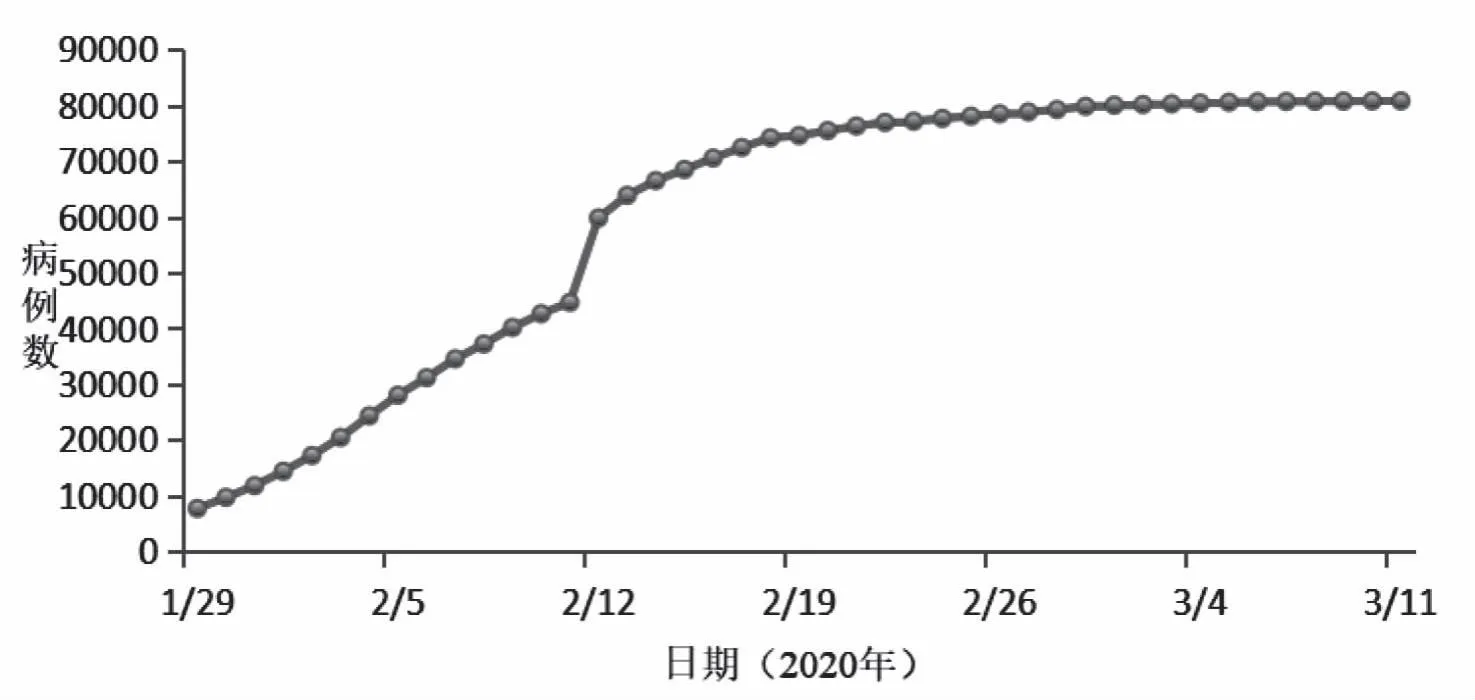
图2 COVID-19全国累计报告确诊病例数变化趋势图[10]

6 结论

本文探讨了曲线拐点的定义、性质(必要条件)、判别(充分条件),还讨论了曲线拐点的计算与应用。拐点是函数的凸凹性分界点,其相关研究具有重要的意义。