基于云模型和D-S证据理论的岩溶盾构隧道掌子面稳定性评价

王 祥 陈发达 吴贤国 冯宗宝 陈虹宇

(1.贵阳城市轨道交通有限公司, 贵阳 550091; 2.华中科技大学土木与水利工程学院, 武汉 430074; 3.南洋理工大学土木工程与环境学院, 新加坡 639798)

轨道交通发展使得岩溶地区盾构隧道工程不断增加,特殊的地质条件引发很多安全问题,特别是对隧道施工至关重要的掌子面稳定性。岩溶环境下的掌子面稳定性问题相比其他工况更加复杂,掌子面失稳或塌陷等安全事故会造成严重人员伤亡和巨大的财产损失。因此对掌子面稳定性进行准确评价并提出有效措施十分重要。

针对岩溶盾构隧道掌子面失稳带来的影响,学者们通过建模、数值或理论分析等对掌子面稳定性进行了研究。安永林等利用强度折减法获取了掌子面临界失稳破坏状态。[1]郭佳奇等研究了断续裂纹的压剪起裂属性的变化规律, 建立了掌子面断续节理防突层失稳突水判断依据。[2]王志杰等构建了掌子面失稳破坏的圆锥台模型,为高压岩溶隧道的设计和施工提供了依据。[3]王秀英等建立了在极限平衡原则之下的掌子面稳定性分析模型和极限支护力计算式。[4]李姝等基于极限分析上限定理和非线性M-C破坏准则分析了深埋盾构隧道掌子面的稳定性状态。[5]杨文钰等基于K-L级数分解法建立了描述土性参数空间变异性的三维随机场,研究掌子面失稳模式和极限支护应力规律。[6]Paternesi等采用三维有限元方法对加筋与无加筋隧道掌子面稳定性进行数值分析。[7]Xue等基于思想点法建立了跨河盾构施工开挖面稳定性评价模型。[8]Li等通过数值模拟和理论分析,评估了在饱和土中挖掘出饱和土的屏蔽隧道的面部稳定性。[9]但这些建模、数值或理论分析没有体现出多因子影响的复杂性,无法处理多源信息的模糊和随机不确定性问题和实现对风险状态的动态管控,而且缺乏对岩溶地质的针对性分析。D-S证据理论对解决“不确定性”“多因素影响”“动态更新”等重要问题是比较好的选择。[10]利用云模型对D-S证据理论进行改进,能够减少多源证据冲突性,处理随机性和模糊性问题以获得更精准可靠的结论。[11]

因此,将基于工程实践和文献研究,选取指标构建框架体系,以评价掌子面的稳定性,并以贵阳市轨道交通3号线太慈桥站为例,提出一种基于云模型和D-S证据理论的岩溶盾构隧道掌子面稳定性评价方法,建立云模型计算掌子面稳定性指标证据,在对多指标证据融合后,使不同时刻证据进行不断更新,从而实现稳定性的动态评价,并基于全局敏感度分析找出敏感因素,为解决岩溶盾构隧道施工过程中的掌子面稳定性评价问题提供思路和对策。

1 理论基础

1.1 云模型

作为一种不确定性转化模型,云模型在处理模糊性和随机性事件方面具有较大的优势。[12]设定量论域U={x},C为U上某个量化区间所对应的定性概念,元素x为C在U上的一次随机实现,μ(x)为x对C的确定度,取值范围[0,1],是有稳定倾向的随机数。

μ:U→[0,1]∀x∈Ux→μ(x)

(1)

x在论域U上的分布称为云,与其对应的确定度组成的数据对(x,μ)为云滴。

(Ex,En,He)为云模型的三个数字特征,其中:期望Ex反映云滴的平均点;熵En是定性概念的不确定性度量;超熵He是熵的不确定性度量,反映云滴的凝聚度。

云图像的生成涉及云发生器,云发生器分为两类:正向云发生器和逆向云发生器。[13]

1.1.1正向云发生器输出云

正向云发生器输出云计算式:

(2)

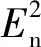
不断重复上述步骤,直至产生n个云滴,形成云。

1.1.2逆向云发生器计算云模型的各种数字特征

样本平均值Ex计算式:

(3)

得到Ex计算样本期望值后,可根据样本计算方差,得到云模型的熵En,超熵He可取常数。

1.2 D-S证据理论

D-S证据理论是一种能够直接表达“不确定”和“未知性”的不确定推理方法。[14]在D-S证据理论中,Θ是辨识框架,这个辨识框架由一系列对象θi构成,即Θ={θ1,θ2,…,θn}。

该理论包括基本概率分配函数m、信任函数Bel和似然函数Pl三个定义,令Θ为一个论域集合,2Θ为Θ的所有子集构成的集合,定义2Θ→[0,1]时函数分别表示为:

(4)

(5)

Bel(A)表示对事件A的信任程度。Pl(A)表示证据对事件A为真的不确定程度。

基于D-S组合规则可同时融合同一个识别框架下的多条证据做出决策,若对∀A⊆Θ,有mi(i=1,2,…,n)为Ai(i=1,2,…,n)的n个基本概率赋值,多条证据的组合规则为:

(6)

式中:k为各条证据之间的冲突系数,k越大,冲突越大。当k=1时,证据之间完全冲突,组合规则不再适用,因此在融合过程中须检验k值的大小。

2 基于云模型和D-S证据理论的盾构隧道掌子面稳定性评价模型

2.1 建立评价指标体系及评价标准

为保证盾构隧道掌子面稳定性评价的适用性,根据已有研究成果[15-17],兼顾各指标间的相关性,遵循系统性和可实现原则,将一级评价指标划分为三大类:岩溶地质因素V1、施工因素V2以及围岩因素V3,其下共选择18个影响因素作为二级评价指标见表1。建立的指标体系如表1所示,其中充填物、地下水和溶洞与隧道的位置关系是定性指标,其余评价因子均为定量指标。通过工程设计资料、地质勘探报告和施工现场监测获取定量指标的实际数据,并利用专家打分法获得定性指标的评分。各个评价指标等级状态划分标准见表1。

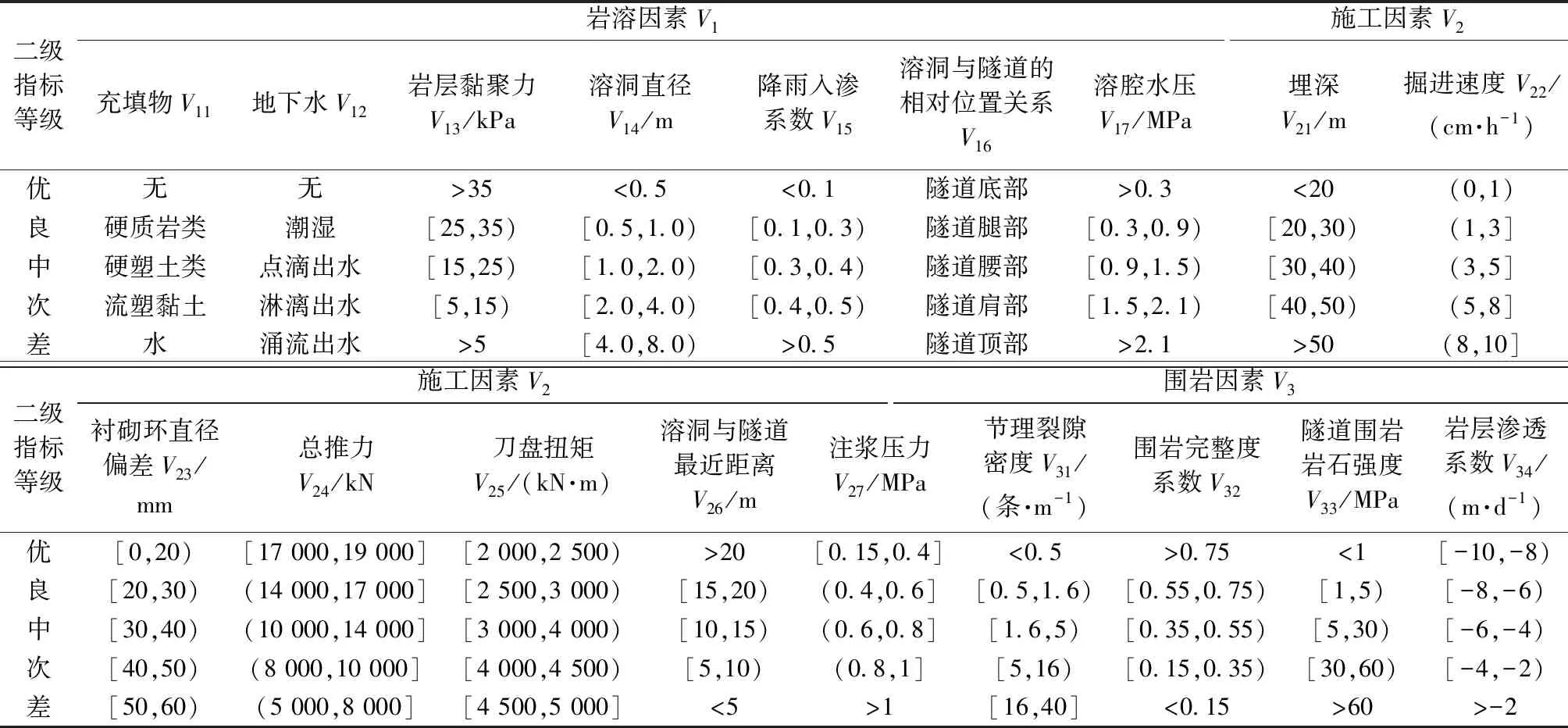
表1 岩溶环境盾构施工掌子面稳定性评价体系指标及评价标准

基于相关文献资料[18-19],参考国内外相关分级标准,将盾构隧道掌子面稳定性分为Ⅰ级(优)、Ⅱ级(良)、Ⅲ级(中)、Ⅳ级(次)、Ⅴ级(差),分级标准具体见表2。

表2 掌子面稳定性分类标准

2.2 基于云模型的证据表达

2.2.1评价指标云数字特征计算

根据表1评价指标等级划分标准,各个评价指标在每个等级下具有一个区间值[Cmin(k),Cmax(k)],因此,云数字特征计算式[20]如下:

(7a)

(7b)

Heij=λ

(7c)

式中:Exij(k)、Enij(k)、Heij分别是指标Dij在第k等级云模型的期望值、熵值、超熵值;λ为常数,可根据实际情况选取。

根据式(7),针对每个三级指标的每一个等级构建一个云模型,确定各评级指标对应各安全等级云模型的三个特征值(Ex,En,He)。

采取专家评分的方法对涉及的几个定性指标:充填物V11、地下水V12、溶洞与隧道的相对位置关系V16以及隧道围岩分级V35进行打分并得出三个特征值。然后利用正向云发生器可以得出各个评价指标所形成的云模型,其中以V13岩层黏聚力以及V23衬砌环直径偏差为例表示出云滴(图1、图2),从蓝色云到绿色云依次表示Ⅰ级至Ⅴ级。

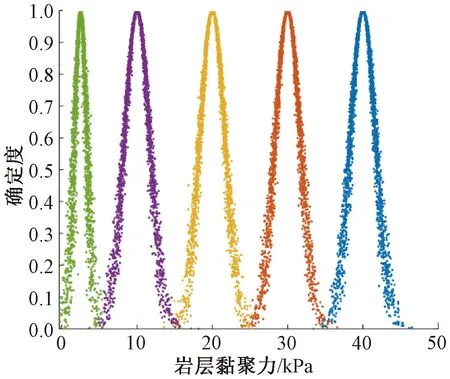
图1 岩层黏聚力云

图2 衬砌环直径偏差云

2.2.2评价指标等级隶属度计算

设xij为收集的评价指标Dij在t时刻的实测值,通过式(8)求得xij对各风险等级的诊断云模型的确定度[21]:

k=Ⅰ,Ⅱ,…,Ⅴ

(8)

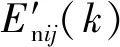
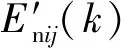
考虑到测量误差、外界干扰等原因,会引起稳定性评价的不确定性,指标不确定的隶属度由式(9)求得:

φij=1-max[μij(Ⅰ),μij(Ⅱ),…,μij(Ⅴ)]

(9)

2.2.3归一化生成证据

由以上步骤得到的隶属度μij(k)表示指标测量值属于各等级云模型的程度。将云模型理论与D-S证据理论相互结合,将D-S证据理论中的基本可信度分配转化为云模型理论中计算所得的隶属度[22]。

指标Dij的各等级隶属度为:

[μij(Ⅰ),μij(Ⅱ),…,μij(Ⅴ),φij]

(10)

利用式(10)对隶属度进行归一化得到证据mij。

(11)

2.3 D-S证据融合和证据更新

2.3.1冲突检测及证据融合

1)识别框架确定。基于上述云模型指标体系等级划分,岩溶盾构隧道掌子面稳定性评价等级被划分为5个等级,因此,D-S证据理论识别框架同样包括五个风险等级和不确定度,表示为:

Θ={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Φ}

(12)

式中:Φ为不确定度。

2)冲突检测。由于传统的Dempster规则无法处理高冲突证据,可利用加权平均规则对不同证据权重进行重新分配。[23]为能够在合适的条件下采取不同的证据融合方法进行信息融合,要判断不同证据之间所存在的冲突程度,冲突程度用冲突系数k的大小确定,k值由式(6)计算可得。当k<0.95时,可以应用Dempster规则,当k>0.95时,可以应用基于加权平均的证据融合方法。[24]

2.3.2证据更新

当冲突处于较小的范围内时,则可以采取传统的Dempster规则[16]进行证据融合,计算式见式(6)。

1)计算不同时刻的证据距离和相似度。

(13)

其中

式中:D是一个2K+1×2K+1的矩阵。

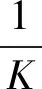
相似度通过式(14)分别计算:

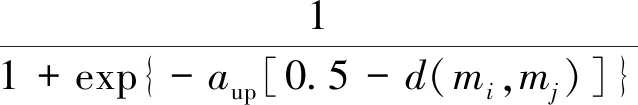
i≠j;i,j=t-2,t-1,t;aup=6

(14)

从式(14)可以得出,当两证据之间的距离越大时,两证据的相似度就会越小。

2)计算证据支持度和可靠度。

mt-2、mt-1,mt三条证据的支持度可由式(15)计算:

i,j=t-2,t-1,t

(15)

mt-2、mt-1和mt各自的可靠度通过式(16)计算:

i,j=t-2,t-1,t(16)

在此基础上,基于可靠度就可以确定不同证据相对重要性权重。

3)计算历史证据权重τt和当前证据权重υt。

证据更新中所用当前时刻证据权重为:

υt=crd(mt)

(17)

则定义历史时刻证据权重为:

τt=1-υt

(18)

4)更新后的证据获取[25]。

在风险评价等级中有5种状态,若式(14)中D=Ⅰ,假设由式(14)得到的t-1时刻证据mt-1(Ⅰ),并且获取了当前证据mt,即有:

(19)

因此,可以计算当前t时刻证据对风险等级为Ⅰ级的概率信度赋值为:

mt(Ⅰ)=τtmt-1(Ⅰ)+υtmt(Ⅰ|Ⅰ)=

τtmt-1(Ⅰ)+υt

(20)

此时,由于命题得到了条件命题的支持,证据更新后的命题t时刻的概率信度赋值mt(Ⅰ)大于或等于t-1时刻mt-1(Ⅰ)。另一方面,由于在条件命题为风险等级为Ⅰ级下,其他风险等级条件命题的概率信度赋值为0,因此风险等级为Ⅱ级的命题更新后概率信度赋值为:

mt(Ⅱ)=τtmt-1(Ⅱ)+υtmt(Ⅱ|Ⅰ)=τtmt-1(Ⅱ)

(21)

其他风险等级的概率信度赋值均按式(11)求出。对于全集Θ的概率信度赋值,有:

mt(Θ)=τtmt-1(Θ)+υtmt(Θ|Ⅰ)=τtmt-1(Θ)

(22)

基于以上步骤可以得出更新后的t时刻的证据。

2.4 敏感性分析

敏感性程度的分析可以得到不同输入因素对输出因素的影响程度,从而制作相应对策降低系统风险。[26]目前应用较为广泛的分析指标为全局敏感度(GSA),Spearman秩相关系数是一种全局灵敏度(GSA)测度,可以判断出两个变量之间的相关性,可以揭示输入和输出因素之间的灵敏度。以GSA(Dij)表示输入特性Dij的全局敏感度可由式(23)[27]表示:

GSA(Dij)=

(23)

GSA(Dij)绝对值越高,评价指标Dij越敏感。GSA(Dij)的正负决定了Dij与评价结果呈正相关或负相关。

3 实例研究

四方河路站—皂角井站区间为贵阳市轨道交通3号线7标部分工程,位于贵阳市南明区皂角井片区。四-皂区间隧道主要穿越地层为中风化白云岩,抗压强度为45～78 MPa,区间钻孔67个,见溶洞的钻孔有14个(直径都大于1 m),钻孔见洞率为21.5%,其中2个溶洞充填率较大,溶洞充填物为软塑—可塑状黏土,局部微含碎石。区间场地地下水主要为潜水,具体可分为第四系松散岩类孔隙水和岩溶水。场地详勘期间测得场区范围内地下水位埋深为1.0～12.5 m,相应标高为1 067.96～1 187.32 m,水位有一定起伏。分析为岩溶裂隙发育得极不均一,白云岩局部隔水又局部含水而形成的复杂水文地质条件所致。

3.1 数据准备和证据获取

选取太慈桥站施工段为例。选择隧道工程领域来自不同单位处于同一层级的3位专家依据现场调研情况和工程资料对V1、V2和V3因素进行独立打分,分数范围为0～100。分别取3位专家评分的均值作为各因素评分分值,获取定性指标的最终数据;并采用实地监测和调研获取定量指标的数据。监测点1在一定时间段t内的指标数据如表3所示。

表3 专家给出的t时刻掌子面稳定性评价

将表2的t时刻运营站点评价指标数据代入计算隶属度值的函数算式中,计算不同时刻数据所对应的评价指标Dij的隶属各个稳定性等级的值。依据最大隶属度原则,最大确定度所在的等级即为该指标对应的稳定性等级状态,通过式(11)对稳定性等级隶属度归一化,形成第t时刻证据mt。重复上述过程依次获得其余时刻的证据。监测点1第t时刻稳定性评价指标对各等级的证据计算结果如表4所示。

表4 第t时刻稳定性评价指标在各等级的可信度分配

3.2 掌子面稳定性评价

通过高冲突证据融合以及低冲突证据融合的方法分别得到了3个二级评价指标的基本可信度分配,结果如表5所示,再将3个二级评价指标的证据进行融合,最终得到岩溶环境盾构施工掌子面稳定性评价结果,融合结果如表6所示。

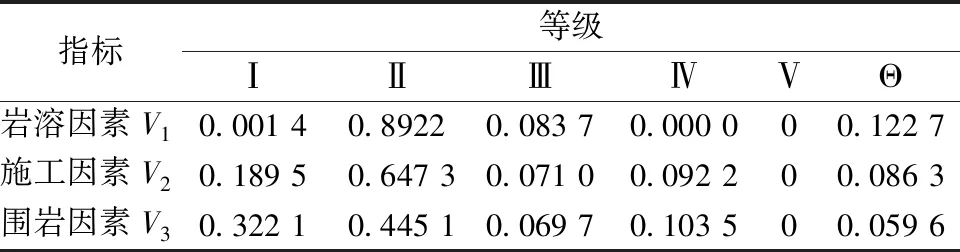
表5 二级评价指标的证据

表6 岩溶环境盾构施工掌子面稳定性评价结果

由表5可知:在证据分类融合的过程中,不确定性系数m(Θ)逐渐减小,说明评价结果的不确定性不断被削弱,不同属性指标证据的基本概率分配可靠性更高,对稳定性评价结果的贡献和解释程度也越大。

在第t时刻,掌子面稳定性状态处于“良”状态。重演求取第t时刻岩溶环境盾构施工掌子面稳定性评价结果的步骤,得到其他时刻的掌子面状态评价结果。通过证据更新得到t-1时刻的历史证据等级Ⅲ即“中”的信度赋值最大,令式(22)中等级为Ⅲ,在已经获取当前t时刻证据m1:t-1(Ⅱ)=Bel1:t-1(Ⅱ)的情况下,有m1:t-1(Ⅲ)=Bel1:t-1(Ⅲ),即可知基于条件化线性组合更新、规则更新后的t时刻证据m1:t如表7所示。

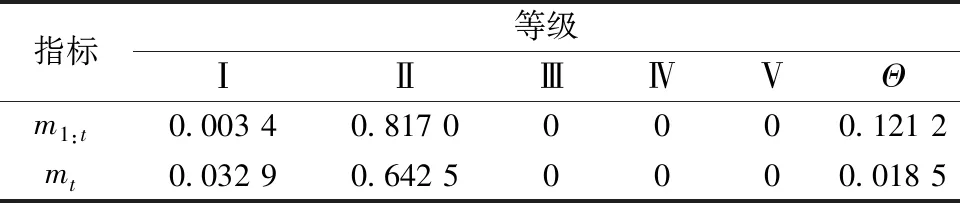
表7 更新后和未经更新的证据

由表7可知:m1:t和mt都是由t时刻监测值计算得到的评价结果,均显示掌子面稳定性状态处于“良”,与实际工程情况相符,但是m1:t在Ⅱ级的基本概率赋值要大于mt,表明进行证据动态更新可以有效地提升证据的可靠性。

3.3 敏感性分析

全局敏感性分析法是研究和分析模型的状态或输出变化对各个输入参数变化的敏感程度的方法,为研究岩溶盾构隧道掌子面稳定性状态变化对各个影响因素变化的敏感程度,将使用Spearman秩相关系数来揭示出各输入因素的全局灵敏度。基于上述数据,图3表示了评价体系中18个影响因子的全局灵敏度的测量结果。

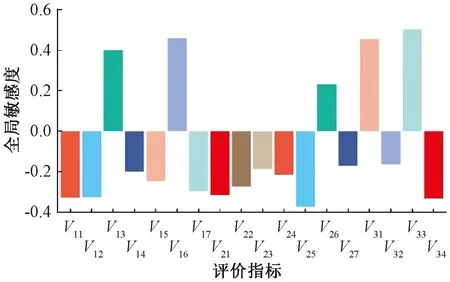
图3 全局敏感度测试结果

从以上全局敏感性测试结果可以看出:

1)各个输入因子对掌子面稳定性的敏感度表现大致呈现正相关和负相关两种状态。呈负相关关系的输入因素增大时,掌子面稳定性就会降低;呈正相关关系的输入因素提高时,掌子面稳定性也会随之变高。为进一步提高掌子面稳定性,应重点关注影响力较大的因素。

2)对于该评价段来说,V16(溶洞与隧道的相对位置关系)、V33(隧道围岩强度)、V31(节理裂隙密度)和V13(岩层黏聚力)为影响掌子面稳定性最敏感的4个因素,故应作为重点关注和管控对象,通过采取加强监测、加固围岩、处理溶洞等针对性处理措施保持掌子面稳定。

3.4 风险管控措施

根据掌子面稳定性评价结果对不同掌子面稳定性等级采取对应的施工控制措施,以指导和反馈施工。主要从溶洞勘探预处理、超前预支护和掌子面核心土预加固等措施控制掌子面变形、维持掌子面稳定,对应如下:

当掌子面稳定性为Ⅰ级时,可不采取超前支护和加固措施;当掌子面稳定性为Ⅱ级,加强监测对发生掉块的地方喷射混凝土封闭,及时采取支护措施,并加强施工过程中的监控测量;当掌子面稳定性为Ⅲ级,采用喷射混凝土或掌子面锚杆注浆加固,对局部掉块严重的地方采用超前小导管注浆加固;当掌子面稳定性处于Ⅳ级时,完善岩溶盾构施工前的岩溶洞穴检测和预警系统,对开挖面附近溶洞进行勘探和注浆充填处理,采用玻璃纤维锚杆注浆加固,开挖后喷射混凝土封闭掌子面,并对掌子面前方实施超前管棚支护;当掌子面稳定性处于Ⅴ级时,加强地质超前预报和现场监测,实施岩溶注浆加固和洞内注浆加固等岩溶处理措施,采用纤维锚杆注浆加固超前核心土封闭掌子面,洞口全断面采用大管棚超前支护,同时优化盾构掘进过程中的施工控制参数,减少盾构机掘进造成的地层损失。

4 结束语

1)将云模型与改进的D-S证据理论模型相结合,基于云模型计算得到的隶属度值转化成D-S证据理论中的基本可信度分配。在信息的融合更新后,通过敏感性分析过程最终形成有效且直观的多源融合和更新的岩溶盾构隧道掌子面稳定性评价方法体系。

2)基于相关工程经验和文献资料,从岩溶因素、施工因素以及围岩因素3个方面构建了岩溶盾构施工掌子面稳定性评价指标体系,并依照相关资料提出了具有科学性的指标评价标准,将综合评价指标划分为5个风险等级,对今后的岩溶盾构隧道掌子面研究具有一定的参考价值。

3)通过证据更新规则有效地提升了证据的可靠性,实现了掘进过程中掌子面状态的动态管控。实例应用的结果表明开挖面总体处于较稳定的状态,并基于全局敏感性分析揭示出各影响因素的敏感性排序,有利于进行岩溶盾构隧道施工的指导和决策。