钢纤维混凝土梁抗剪强度的集成学习预测方法*

狄春锋

(中铁建设集团有限公司, 北京 100043)

0 引 言

钢混结构的剪切破坏可能会导致结构突然失稳并引发严重的安全事故,因此,提升钢混结构的抗剪承载力至关重要。钢纤维混凝土(SFRC)是在普通混凝土中掺入适量、不规则分布的短钢纤维(SF)所形成的一种多相多孔复合材料,这些不规则分布的SF能有效地阻止混凝土内部宏观裂缝的形成及微裂缝的扩展,显著改善SFRC的抗拉、抗弯和延性性能等[1],进而提升结构的物理、力学性能及耐久性[2]。

准确地计算或预测SFRC结构的极限抗剪性能有利于结构设计研究[3]。但传统方法具有不同的局限性,模拟试验耗时耗力,且无法大量、快速地得到不同工况的极限抗剪性能[4];则统计公式则难以考虑所有的抗剪性能影响因素[5];而有限元法需要详细的本构信息才能计算,且一次只能计算一个结构或构件,耗时较长,有时有限元计算和热力学的结果也会有所出入,这证明有限元模拟法也有所局限[6]。尽管SFRC结构的抗剪性能已有过相关的研究,但在许多方面仍有改善的余地,且目前仍未得到普适性的预测方法。

近年来引入的机器学习算法可能为普适性抗剪性能预测提供新思路。机器学习主要研究计算机模拟或实现人类的行为,通过学习获取新的技能和知识,完善自身已有的知识结构,并不断提高自身的性能。机器学习在土木工程领域已有诸多应用,包括健康监测、性能预测评估等[7-8]。性能预测的应用包括抗剪性能的评估,如文献[9-10]使用人工神经网络对钢混构件的抗剪性能进行预测,并与3种现行抗剪设计方法对比证明人工神经网络可以得到更优的结果;Yaseen等结合粒子群优化的人工神经网络算法对钢混梁的抗剪性能进行预测[11],输入参数为几种材料性能和尺寸,并识别不同参数对抗剪性能的影响程度,最后用元启发式优化算法对其进行验证;Zhao等用反向传播神经网络成功预测钢混梁结构的挠度[12],采用了120种梁的几何与力学性能数据,划分了7个数据集进行对比。

机器学习在土木工程领域应用最多的算法依旧是人工神经网络,而集成学习的引入,可以改善神经网络的可解释性差、需要数据量较大、计算成本昂贵等缺陷。集成学习本身不算一种单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。集成学习集百家之所长,能在机器学习算法中拥有较高的准确率,目前在土木工程领域已有部分应用。文献[13-14]基于集成学习算法完成了混凝土的配合比设计的工作,并得到不同因素对配合比的影响程度及对应的解决方案,成功地得到了抗冻性和成本优化的配合比方案;Gong等用集成学习预测沥青混凝土的弹性模量[15],与Witczak公式计算结果相比预测精度提升22.5%,计算时间仅略微有所增加[16];Huang等基于几种集成学习算法研究了钢混框架结构平面内失效模式[17],其中准确度最高的达到了85.7%,且大部分都超过了80%。

为建立准确高效的SFRC梁结构的抗剪性能预测模型,提出了一种基于集成学习算法评估结构抗剪性能的模型,只需输入相应的参数,即可在几秒内得到SFRC梁结构的抗剪强度。首先,用热力图分析方法直观、线性地研究各参数之间的关系,判断输入参数之间是否有冗余度,并判断输入是否与输出之间有强相关性;其次,基于弱学习器、Bagging(RandomForest)和Boosting(XGBoost、AdaBoost和GradientBoost)三类算法对抗剪性能进行预测,并对比测试集和训练集的计算过程,验证模型的泛化性;最后,使用k近邻算法(KNN)、核脊回归(Rigde)、Lasso回归(Lasso)与多元线性回归(MLP)四种常用的回归模型与集成学习计算的结果进行对比,验证模型的高效性及可行性。

1 数据集

1.1 数据集的来源与预处理

机器学习通常需要的数据量较大,但鉴于工程领域的数据较少,且通过试验或实际工程所得数据较为困难,而对抗剪性能的研究文献中已积累了不少数据,因此本研究的数据从文献中收集。因研究的目的为建立有效的模型,为此数据并未穷尽所有相关文献,仅选取了代表性的330组数据,数据量虽不大,但参数具有代表性,均为对抗剪性能产生影响的重要参数[1]。

本研究使用自助抽样法划分数据集。具体数据的分析如表1所示。数据集包含8个参数:梁有效高度d、梁有效宽度bw、纵向配筋率ρ、混凝土的抗压强度fc、骨料尺寸da、剪跨比a/d、纤维抗拉强度ft、钢纤维系数Fst、抗剪强度Vu作为输出参数。表1分别展示了各参数的均值、方差以及最大值和最小值。

表1 数据集的统计分析

1.2 参数的相关性分析

利用热力图可以看出数据表里多个参数两两的相似度,从而可展示参数的相关系数矩阵,其相关系数计算公式见式(1)。

(1)

式中:ρ为相关系数;X1和X2为任意两个参数;Cov为协方差;E为数学期望;D为方差。图1展示了所有参数之间的热力图关系。热力图的颜色越深,表示线性相关程度越高;对于相关系数小的两个参数,只能说明二者的线性关系程度弱,但不能说明参数之间不存在其他的相关关系,如曲线关系等。可以看出:

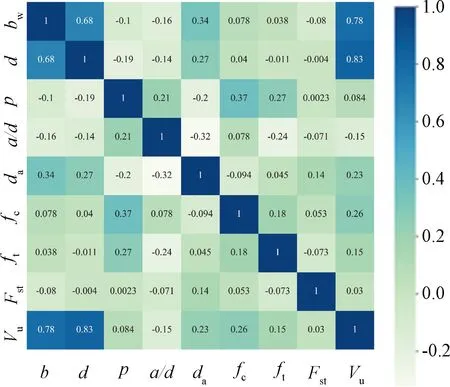
图1 参数热力图分析

1)钢纤维混凝土结构的抗剪性能与梁的有效高度和宽度的线性关系程度最高,分别为0.83和0.73,这证明梁的尺寸对抗剪性能有直接相关的影响,在结构设计中应着重考虑。

2)其他参数对抗剪性能的线性影响较弱,应进一步考虑是否有其他关系存在。

3)输入参数之间的线性关系均较弱,这证明至少在线性关系程度层面,输入参数的独立性较强,均可同时作为输入来建立模型,互相干涉影响的可能性较低,从侧面可以印证模型的鲁棒性较强,适用性也较强。

2 集成学习算法

集成学习的思想是组合许多的弱学习器以得到一个预测效果较好的强模型。集成学习对于不充分数据有很好的效果,适用于钢混结构领域性能预测数量不够充分的数据集[18]。常见的集成组合策略主要包括Bagging和Boosting两类。其中,Bagging利用不同估计算法结果的平均值进行预测,Boosting算法通过一系列聚合的估计模型的加权平均值进行预测。图2展示了集成学习通用的原理,从样本集中依据两类抽样方法Bagging和Boosting抽取数据,通过不同的集成学习算法组合弱学习器,将学习器和样本分别加权,得到强学习器,最后输出结果。其中,同类的弱学习器称之为同质的基学习器,不同类的弱学习器称之为异质的组件学习器。常见的弱学习器包括支持向量机(SVM)、逻辑回归、神经网络以及CART决策树等。

图2 集成学习原理

2.1 常用的弱学习器

2.1.1DecisionTree算法

DecisionTree算法是运用于分类的一种树结构,其中的每个内部节点代表对某一属性的一次测试,每条边代表一个测试结果,叶节点代表某个类或类的分布。其构造分为生成和剪枝两个步骤:由数据集生成,递归选择最优特征;剪枝检验生成的结果,可以将树变得更简单并使它具有更好的泛化能力。优点包括分类精度高、生成的模式简单、对噪声数据有很好的健壮性等,是应用最广泛的弱学习器。

2.1.2ExtraTree算法

ExtraTree算法由许多DecisionTrees构成,收集多个去相关树的结构,聚集起来输出分类结果,每棵树都有一个随机样本,样本有多个特征,每棵树都必须从这些特征集中选择最佳特征,然后根据一些数学指标(本文用基尼指数)拆分数据。ExtraTree算法的随机包括特征随机、参数随机、模型随机和分裂随机。

2.2 RandomForest算法

传统的Bagging抽样方法会从原始数据集中重复抽取子样本,将多次采集到的样本集作为训练集,而原始数据集中没被抽取到的样本作为测试集。图3展示了RandomForest算法流程的一部分,首先,从样本中随机抽取子样本建立子训练集,每个节点分裂之前随机选择特征生成特征子集,建立决策树,对结果进行一票制投票。与Bagging方法相比,多了一次针对特征的随机选择过程。RandomForest算法与ExtraTree算法十分相似,都由许多DecisionTrees构成,二者的主要区别包括:ExtraTree使用所有的样本特征随机选取,完全随机地得到分叉值;RandomForest平均结果,在随机子集内得到最佳分叉属性。

图3 随机森林算法示意

2.3 Boosting族算法

2.3.1XGBoost算法

XGBoost算法通过优化结构化损失函数,加入正则项的损失函数,起到降低过拟合的风险程度,实现弱学习器的生成,并且没有采用搜索方法,而是直接利用了损失函数的一阶导数和二阶导数值,并通过加权分位数、预排序等方法对性能进行提升。

2.3.2AdaBoost算法

AdaBoost算法通过不断地模型迭代,更新样本的权重,其每次用的数据点均相同,只是权重值不同。分类误差越大,则对应的弱学习器权重系数越小,即误差率小的弱学习器权重系数越大。每一次生成的子模型,都是生成拟合结果更好的模型。采用加权平均方法进行融合,得到最终的强分类器。该算法具有原理简单、分类精度高、能使用各种分类模型来构建弱学习器、不容易过拟合等特点。

2.3.3GradientBoost算法

GradientBoost算法的思想是借鉴于梯度下降法,基本原理是根据当前模型损失函数的负梯度信息来训练新加入的弱学习器,然后将训练好的弱分类器以累加的形式结合到现有模型中。实质是基于Boosting集成思想的加法模型,训练时采用前向分布算法进行贪婪的学习,每次迭代都学习一棵决策树来拟合之前的树的预测结果与训练样本真实值的残差。XGBoost实质上是GradientBoost的极限状态。

3 试验与分析

3.1 试验环境

本文的程序使用Anaconda Navigator软件平台中的Jupyter Notebook模块进行搭建,基于Python 3.7编程语言及建立在Numpy、Pandas和Matplotlib之上的Scikit-Learn工具库进行集成学习算法的编程计算。基于交叉验证方法进行自动调参,在缺省参数的基础上调整为合适的超参数,使模型得到其能力的最优结果及较优的泛化性能,使用语法示例如下:

from sklearn.ensemble import RandomForestClassifier

clf=RandomForestClassifier(n_estimators=10,max_features=2)

clf=clf.fit(X, y)

scores=cross_val_score(clf, X, y)

3.2 试验结果与分析

表2展示了各算法的决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE),见式(2)。决定系数的值越大,自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比越高;RMSE和MAE的值越低,误差越小,预测的准确度越高,但RMSE与MAE更多地表征模型的稳定性,而非准确度。

(2a)

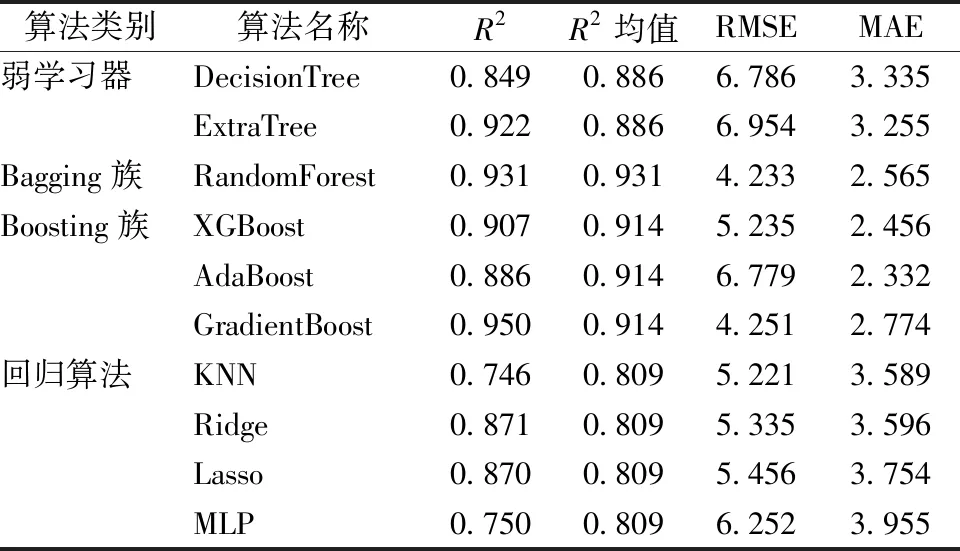
表2 算法计算结果对比

(2b)

(2c)

图4展示了各算法准确度的计算过程,包括集成学习所需要的弱学习器(图4a、b),典型的集成学习两族算法(图4c～f)。

a—DecisionTree; b—ExtraTree; c—RandomForest; d—XGBoost; e—AdaBoost; f—GradientBoost; g—KNN; h—Rigde; i—Lasso; j—MLP。

1)图4a～j都展示了在测试集和训练集的计算结果对比,测试集的结果相较于训练集差一些,但测试集的准确度也无限趋于训练集,证明模型均未过

拟合,可拓展性较强,即模型的泛化性较强。随着数据的逐渐积累,测试集的结果可能会与训练集一样好。

2)结果最优的为Bagging族算法,其次是Boosting族算法,这证明集成学习预测SFRC结构的抗剪性能的模型的准确度较高,模型的预测能力相对稳定,可以推广应用。

3)在集成学习诸多算法的结果中,又以RandomForest算法和GradientBoost算法最优,准确度分别达到了0.931和0.950,且RMSE和MAE的值也显示模型的稳定性较好,证明这两种算法最适用于抗剪性能的预测。另外,GradientBoost算法能灵活处理各种类型的数据,包括连续和离散数据,且易于特征组合和选择,调参相对少,这使其更易于无机器学习算法基础的工程设计从业者快速、高效的使用。总之,这两种算法都是集成学习中的代表性算法,也被证明具有高效、精准的计算能力,二者的集成思路不同,GradientBoost是多棵树累加之和且只能顺序生成,而RandomForest是多棵树进行多数表决且可以并行生成;前者是依据偏差优化,后者是方差优化;前者是全样本训练,后者是有放回的抽样训练。二者各有利弊,在计算时最好两个算法都用,使结果互相印证。

4)弱学习器的准确度不如集成学习算法,准确度的均值只有0.886,证明集成了各弱学习器的模型更适用于本研究,可以更好地对钢混结构抗剪强度进行评估预测。需要注意的是,ExtraTree比RandomForest算法更具有随机性,因该算法不需选择最佳阈值,而是采用随机阈值进行分枝;并且这种增加的随机性有助于创建更多彼此独立的决策树,各个子决策树越独立,综合的效果就越大于大数定律。这两点也是ExtraTree的准确度仅次于RandomForest算法结果的原因。

5)XGBoost算法虽然是基于GradientBoost的极致梯度提升算法,两者思想基本相同,但做了一些优化,包括二阶导数使损失函数更精确、正则项避免树过拟合以及Block存储可以并行计算等。但XGBoost准确度只有0.907,并不如GradientBoost的0.950,这说明优化并不一定会使模型的准确度提升,因此不可一味地使用最新的优化算法,有时经典算法可能更适用。

6)本研究还使用4种回归算法对数据集进行计算,包含k近邻算法(KNN)、核脊回归(Rigde)、Lasso回归(Lasso)与多元线性回归(MLP),结果展示在图4 g-j与表2中,可以看出,回归算法的准确度均未超过0.900,均值只有0.809,且稳定性也较弱,比几种集成学习算法的表现差,这证明了集成学习模型在计算强非线性系统的数据集时表现更好,而回归算法的表现较差,并不适用。

4 结束语

本文建立了钢纤维混凝土结构抗剪性能的机器学习预测模型,采用了集成学习算法对文献中的数据进行建模,得到了如下结论:

1)准确度最优的GradientBoost模型达到了0.950,充分证明了模型的有效性,可以准确地预测SFRC结构的抗剪性能。

2)测试集与训练集的计算过程对比证明了模型的泛化性较高,可拓展应用。

3)集成学习中Bagging族算法比Boosting族算法的结果更优,其中的GradientBoost与RandomForest最优。

4)集成学习的准确度和稳定性均高于传统回归算法,证明集成学习更适用于SFRC结构抗剪强度预测问题。

未来的研究方向是选用集成学习模型中表现较优的模型进行不断优化,并依据文献、实体工程数据等来源不断拓展数据集的参数及数量,分析不同参数对预测结果的影响程度及相关关系,以便得到结构性能与各输入参数的简化数学关系式,最终使模型可实际应用于工程设计与研究。