基于云贝叶斯网络盾构下穿铁路近接施工安全风险动态评价*

周 立

(武汉地铁集团有限公司, 武汉 430040)

0 引 言

随着我国地铁轨道交通和高速铁路的飞速发展,地铁隧道区间下穿铁路施工现象越来越普遍。在盾构下穿铁路工程中,施工阶段是主要的风险源头。为了控制盾构推进过程中对周围环境的影响,限制地基和轨道变形,保障上部铁路的正常运营,开展盾构下穿铁路施工过程风险动态评估与决策,对施工过程中的风险状态进行实时监控与预警具有重要研究意义。

国内外对于盾构隧道下穿铁路施工安全影响研究主要有理论分析法、数值模拟、模糊评价等方法。Shi等基于弹性理论建立土体-隧道相互作用弹性模型,利用随机介质理论预测盾构施工引起的地表移动变形[1]。Wang利用数值模拟针对黄土层浅埋双连拱隧道穿越对既有铁路运营安全影响的特点,提出铁路路基和轨道沉降的控制标准[2]。陈海丰等基于理论分析和三维数值仿真研究了软弱地层地铁盾构下穿高铁的安全控制技术[3]。马相峰等通过数值模拟对地铁盾构下穿多股道铁路路基变形控制优化进行研究[4]。祝嘉辉等结合现场资料探究下穿施工时既有高铁线路沉降规律及盾构施工参数控制[5]。薛春瑞将调查打分法和数值模拟相结合,建立了盾构隧道穿越既有高铁风险评价模型[6]。林大涌等通过层次分析法识别风险因素,利用模糊集理论建立了风险模糊综合评价模型[7]。上述研究主要集中于沉降变化规律分析,对风险管理研究不充分,传统的评价方法局限于静态推理,难以反映风险演化过程。

盾构下穿铁路施工安全涉及的致险因素繁杂多样,由于监测数据的不确定性和多源复杂致险信息的动态变化,对盾构下穿铁路工程安全风险进行实时监控与更新管理十分重要。贝叶斯网络可以很好地用于知识表示和概率推理,云模型将定量数值转化成定性概念时能充分表达模糊不确定性,使用云模型可以将贝叶斯网络节点的数据转化为处于各个属性状态的确定度,进而实现网络节点的离散化,同时描述了定性概念的模糊性。本文将云模型和贝叶斯网络结合,建立云贝叶斯网络的动态风险分析模型,可根据系统中实时获取的证据实现模型的更新[8],解决了传统风险分析方法在动态风险评价问题中的限制。盾构下穿铁路首先对盾构下穿铁路施工致险因素进行分析,根据专家知识和工程经验建立施工安全贝叶斯网络,利用云模型离散节点数据获取先验概率,基于贝叶斯网络进行风险概率推理、敏感性分析和逆向诊断,使用综合云获得系统节点最终的风险值,为工程施工安全风险的实时监控与预警提供决策支持。

1 理论基础

1.1 云模型

云模型是用语言值描述的某个定性概念与其数值表示之间的不确定性转换模型[9]。设U是一个论域U={x},T是与U相联系的语言值。U中的元素x对于T所表达的定性概念的隶属度CT(x) (或称x与T的相容度)是一个具有稳定倾向的随机数,隶属度在论域上的分布称为隶属云[10]。CT(x)在[0,1]中取值,云是从论域U到区间[0,1]的映射,即CT(x):U→[0,1],∀x∈U,x→CT(x)。

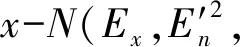
(1)

1.2 贝叶斯网络

贝叶斯网络(BN)结构是一个有向无环图,由代表随机变量的节点以及连接节点的有向边构成。有向边,表示了节点之间的条件依赖关系,从父节点指向子节点。若节点之间没有有向边,则说明它们相互独立。条件概率用于定量地描述节点之间的依赖关系,是BN建立和推理的基础。对于没有父节点的节点,利用边缘概率分布表达信息。

贝叶斯的推理是基于贝叶斯公式(2)[8]进行的,给定变量B一种状态b,对于变量A的状态aj,j=1,2,…,k,可用公式(3)表示概率关系:

(2)

(3)

其中P(A=aj|B=b)是观察证据b成立A=aj假设成立的概率,P(B=b|A=aj)是当aj为真时,B=b被观测到的可能性。P(A=aj)是假设成立的可能性,P(B=b)是证据发生的概率,P(A=aj|B=b)和P(A=aj)分别被称为后验概率和先验概率。

2 基于云贝叶斯网络动态安全风险评价模型

为了实现盾构下穿铁路近接施工风险的动态评估,本研究开发了基于云贝叶斯的安全风险评价推理模型。它主要包括以下几个步骤:1)贝叶斯网络构建;2)云模型获取先验概率;3)云贝叶斯前向推理预测;4)事中、事后保护。图1为所提出方法的流程图。

图1 基于云贝叶斯网络的施工安全动态评价方法流程

2.1 贝叶斯网络构建

2.1.1建立盾构下穿铁路施工风险评价指标体系和标准

一般情况下,导致隧道施工安全事故的主要原因可分为3个方面:不良地质条件、设计和施工参数不当、管理不善[8]。通过查阅大量文献以及对盾构下穿铁路施工安全事故工程经验的总结,威胁施工安全的影响因素主要分为地质条件、隧道相关参数、

既有铁路风险、和施工参数4个层面。地质条件主要包括:土体压缩模量(C1)、黏聚力(C2)、内摩擦角(C3)这三个方面,隧道相关参数主要涉及:新建隧道直径(C4)、新建隧道埋深(C5)、穿越空间夹角(C6)、近接空间距离(C7)[13-15]4个方面,既有铁路风险主要涉及既有铁路等级(C8)、运营时速(C9)[16]、铁路路基沉降(C10)、轨道差异沉降(C11)4个方面。在地铁盾构开挖施工阶段,确定合理的盾构机械施工参数对隧道施工及周围结构安全具有重要的意义。其中土仓压力(C12)、注浆压力(C13)、推进力(C14)、推进速度(C15)是施工过程中影响地基变形和结构变形的主要因素[17],因此盾构施工参数涉及4个方面。

为了便于评价系统的风险状况,基于大量工程实践、仿真和文献总结,参考相关规范要求[18-19],将盾构下穿铁路施工阶段的安全风险总体水平(T)划分为1(安全)、2(低风险)、3(中风险)、4(高风险)、5(极端风险)5个等级,对每个指标对应的风险等级取值范围进行划分。客观因素基于现场监测及工程数据进行衡量,主观因素由专家打分进行评判。评价指标安全风险等级划分标准和取值范围如表1所示。

表1 评价指标及标准

2.1.2贝叶斯网络模型设计

首先基于2.1节中建立的盾构下穿铁路施工风险指标体系创建BN节点,然后通过分析节点之间的因果关系建立风险因素与目标风险事件之间有向性的逻辑关系,从而形成网络结构。在隧道施工领域,经过大量实践积累了丰富的工程经验,涉及专家知识的利用和故障树转化是建筑领域用于创建BN结构的有效方法。除此之外还要构建条件概率表(CPT),它是反映变量之间关联性的联合概率分布集,贝叶斯网络的定量推理是以它为前提和基础实现的。

2.2 节点离散化

构建贝叶斯网络时,所开发的节点状态为连续型变量或者混合变量,通常会造成具有连续父节点的离散子节点的条件概率无法确定,在使用上存在限制从而造成模型的精度下降,推理结果出现偏差。在云BN中,应用云模型的前向云算法对连续型节点数据的进行离散化处理,并转化成先验概率。

2.2.1定义云族

定义F为贝叶斯网络中某连续型节点的归一化风险论域,F=[0,1],D1,D2,…,Dn是论域F的两两无交集的充分完全划分,F1,F2,…,Fn是相对于n个划分的定性概念语言表示,即n个风险等级,对应的在论域F上生成n个相邻的风险云族CloudF1,CloudF2,…,CloudFn。表2表示了论域上n个相邻风险云族的定义。利用前向云算法根据输入云数字特征生成大量云滴,用来生成云滴的云发生器的数字特征由表2得到。

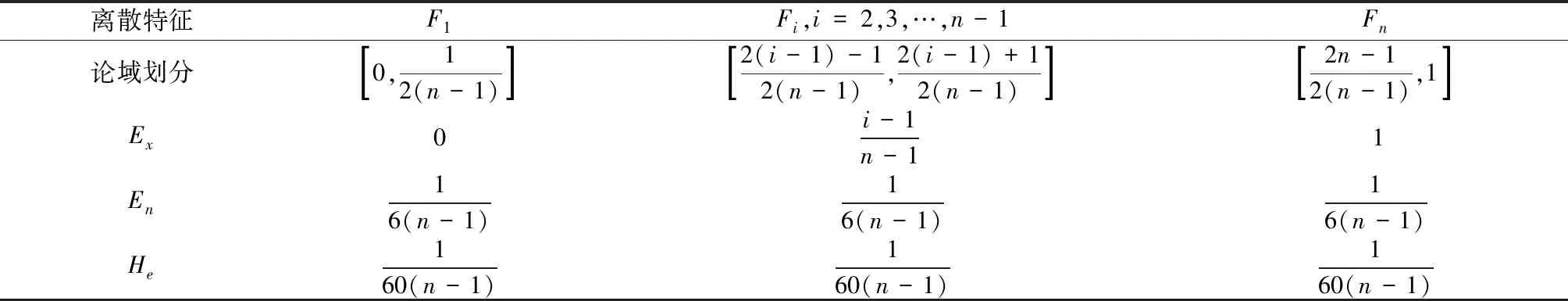
表2 n个风险云族的划分及数字特征

在正态云中,[Ex-3En,Ex+3En]区间对可涵盖99.74%的云所表示的概念,符合正态分布中的“3σ”原则。因此为了保证论域上的各个云能够很好的区分,并保留其表达优势,将云所接受的定性概念的范围即云的熵设为论域宽度的1/6,云的超熵根据经验设为熵的1/10。

2.2.2节点数据归一化处理

贝叶斯网络中各父节点的数据属性、取值范围等均有所不同,为了将变量的信息映射至风险论域的云族中,需要对所有变量进行归一化处理,将规范后的数值综合到[0,1]区间。式(4)给出了取值区间为[m,n]的变量归一化公式。

(4)

根据式(4)可得上述指标的归一化表达式,例如新建隧道直径(C4)如式(5)所示。

(5)

2.2.3确定度-先验概率转换

将得到的归一化变量值u,作为定性概念Fi的一次随机实例,输入到基于MATLAB代码构造的前向云发生器中,可获得云滴drop(u,μ),其中μ是u值对CFi的确定度。式(6a)给出了计算确定度μ(u)的过程。云模型定义了确定性程度,贝叶斯网络推理需要输入概率,利用式(6b)将确定度转换为BN源节点的先验概率。

(6a)

(6b)

式中:α为一致性参数,取值在(0,1]之间。α越大,表明确定度与概率转换保持的一致性越高,这里建议使用α=1以达到最大的一致性。

2.3 风险值输出

为了消除观测信息确定度计算过程中的随机性对最终系统风险评估值的影响,对于云模型转化得到的观测节点在各个风险状态的边际分布概率进行多次重复计算,并输入到云贝叶斯网络中进行迭代推理,通过概率聚合获取各个风险等级的概率分布结果,将风险等级划分为n个水平,表示为{F1,F2,…,Fn},设定Rj(Fi)是利用云贝叶斯网络风险度量结果j隶属于风险水平Fi的概率,用Rj={Rj(F1),Rj(F2),…,Rj(Fn)}表示。经过k次重复推理获取k个计算结果{R1,R2,…,Rk},对{R1,R2,…,Rk}进行概率合成得到式(7),式(8)表示了风险水平Fi下k个结果的聚合概率。

R={R(F1),R(F2),…,R(Fn)}

(7)

i=1,2,…,n;j=1,2,…,k

(8)

为了进一步的反映风险概率的不确定性程度,通过正态云模型生成综合云的方式获取具体的不确定风险值。因此本研究可根据表1中的云特征值,由云模型运算法则可得到综合云CZ参数(ExZ,EnZ,HeZ)。它综合了概率和不确定性,更加全面地反映了风险度量结果。

(9)

2.4 敏感性分析和风险诊断

本研究利用敏感度性能度量(Sensitivity Performance Measure,SPM)来评估每个风险因素变化对风险事件的贡献程度,确定关键的风险因素,以帮助决策者明确施工过程中的监测和控制重点,从而有针对性地采取管控措施。假设根节点风险因素为Ci(i=1,2,…,n),ci表示每个根节点的状态,叶节点风险事件为T,SPM(Ci)作为衡量根节点灵敏度的指标,计算式如式(10)所示。

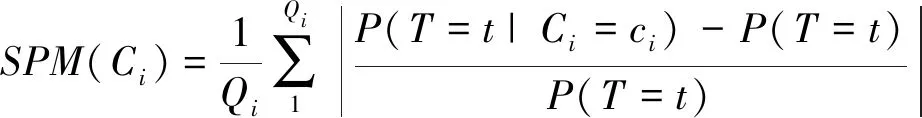
(10)

式中:Qi是Ci的状态个数。SPM(Ci)越接近于1,说明根节点的敏感度越大,应当重点关注。

风险诊断分析旨在涉及不可避免发生事故的情况下,计算各危险因素Ci的后验概率分布。致险因子Ci的后验概率用P(Ci=c|T=t)来表示,如式(11)所示。

i=1,2,…,n

(11)

其中P(Ci=c|T=t)越高,更接近于1,可将Ci视为造成事故T=t可能性最大的致因,可快速查明最可能导致故障的致因组合,使得安全事件得到有效控制,降低风险程度避免事故的进一步恶化。

3 实例分析

3.1 工程背景

武汉市轨道交通6号线唐家墩站～石桥路站区间约右K25+495～K25+595范围内下穿京广铁路等股道群,共有12股道(其中汉孝城际高架2股道在建、京广上下行线2股在建、城际场京广上行联络线1股道在建)。下穿长度约100 m,区段线间距约10.2～10.7 m,隧道顶覆土厚度约22 m,区间隧道采用2台土压平衡式盾构机进行掘进,盾构机从石桥路站先后始发,掘进至唐家墩站吊出,盾构开挖区域所在土体为淤泥质粉质黏土夹粉土、粉砂。

3.2 盾构下穿铁路施工安全贝叶斯网络构建

根据表1给出的盾构下穿铁路施工风险指标体系,整合事故树及专家经验等先验知识,得到安全风险分析贝叶斯网络拓扑结构,并建立关联父节点与子节点的条件概率表,构建模型如图2所示。根据2.1.1节中的安全风险评价标准,贝叶斯网络中每个节点都有5个状态,叶节点T表示的事件为系统总体风险,B1～B4,为中间节点,是影响风险的4个关键因素类别。C1～C15,15个指标为输入变量是网络中的根节点。

图2 盾构下穿铁路施工系统风险的贝叶斯网络模型

3.3 云模型离散化处理

选取该工程下穿其中一高铁工程盾构施工段某截面作为研究对象,收集对应指标体系的数据,使用归一化公式对原始数据进行处理,表3给出了用于该截面盾构下穿铁路施工安全风险分析的BN网络各节点的观测值。

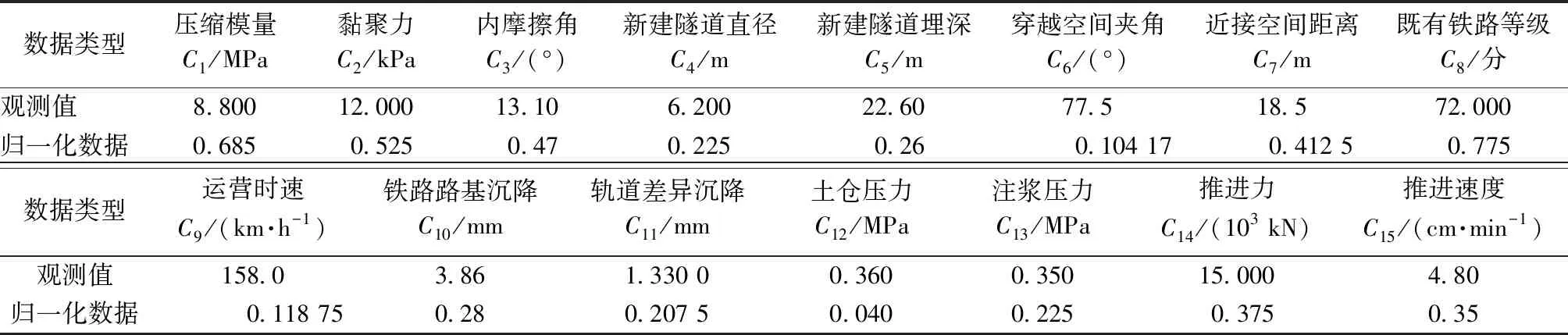
表3 贝叶斯网络各节点变量的观测值

在[0,1]的论域上将风险云定义为5个相邻的云族,依据表2将系统风险云族划分为CloudF1(0,1/24,1/240),CloudF2(1/4,1/24,1/240),CloudF3(1/2,1/24,1/240),CloudF4(3/4,1/24,1/240),CloudF5(1,1/24,1/240),分别表示1(安全)、2(低风险)、3(中风险)、4(高风险)、5(极端风险)5个等级。图3表示了风险云族的示意图。

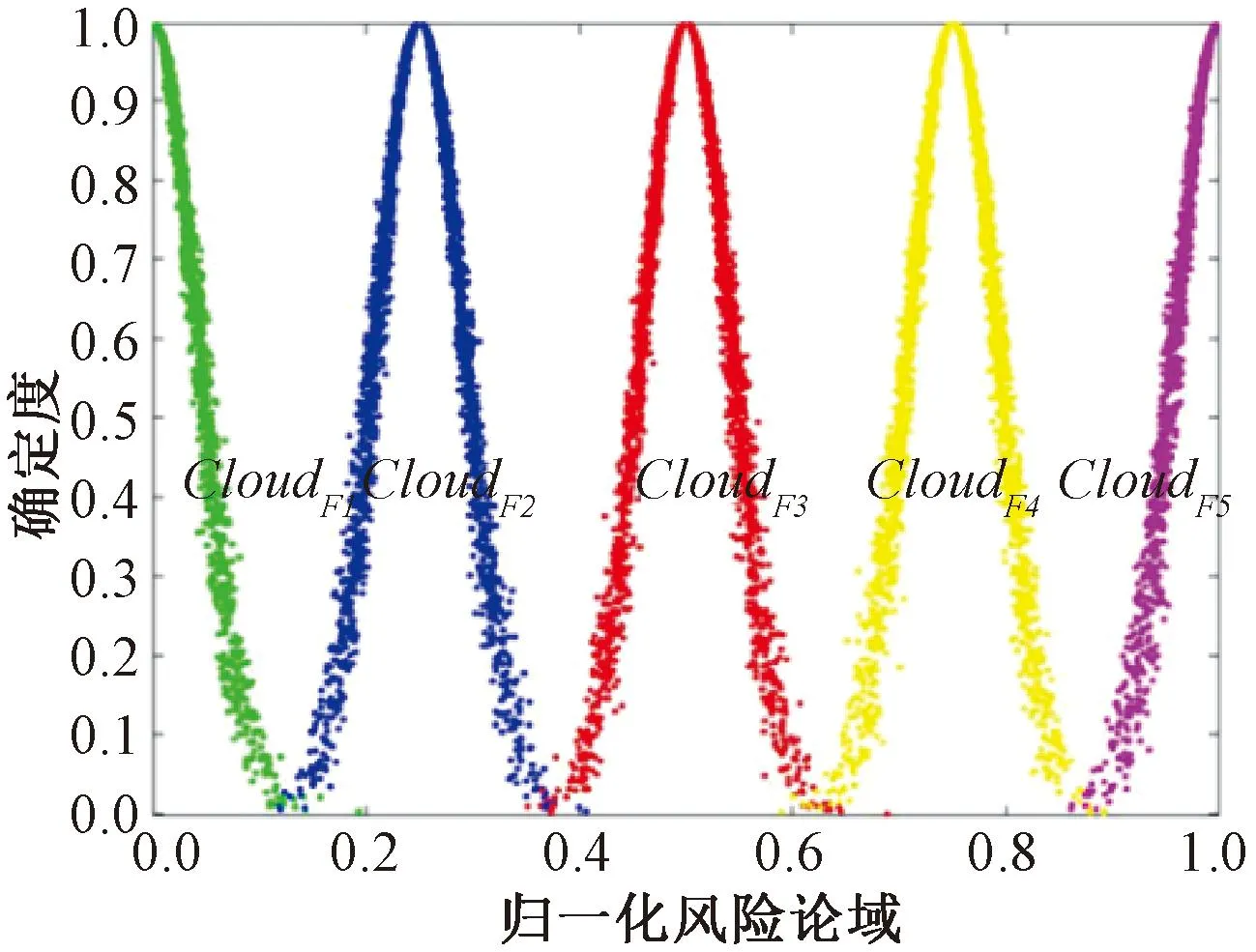
图3 风险云族示意

3.4 风险推理预测

将表3中的归一化数据和图3定义的云族代入2.2节中的式(6a),根据前件云算法产生观测值对

各云族的100组确定度并利用式(7)转化成先验概率输入BN,利用构建的贝叶斯网络重复推理100次,通过2.3节中式(7)和(8)对100组风险概率分布进行聚合。表4给出了最终各类型节点风险状态的聚合概率。

表4 不同类型风险的聚合概率分布

根据式(6a)计算综合云的数字特征,并生成综合云的云图如图4所示。由表4可知,叶节点T风险等级为3状态的聚合概率最大,为0.383 9,在风险状态为2等级取得第二大聚合概率为0.298 8,结合图4可知,叶节点T的综合云期望值为0.319 6,处在2级风险和3级风险水平之间,因此可以得到该盾构下穿铁路工程研究截面施工安全风险等级为3级(中风险)水平,并有向2级(低风险)状态发展的趋势,整体上来说该工程研究截面需要进一步加强风险管控,通过采取一定的措施将风险水平进一步降低。

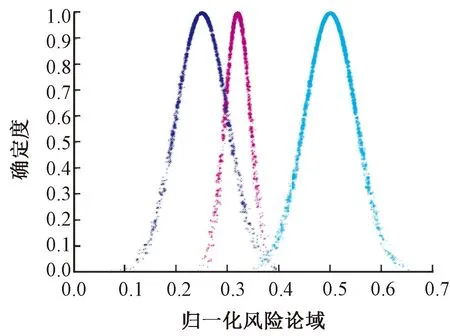
二级云; 聚合云; 三级云。

进一步分析可以看出土质条件B1相关的风险和盾构施工参数B4相关的风险较高,B1安全状态处于3级(中风险)水平,有向4级(高风险)水平转化的趋势,B1安全状态处于3级(中风险)水平,有向4级(高风险)水平转化的趋势,B4安全状态处于3级(中风险)水平,有向2级(低风险)转化的趋势。隧道相关参数B2、既有铁路风险B3的安全等级均为2级,有向3级转化的趋势,B1的风险值大于B4大于B3大于B2,因此可基本判断导致该截面下穿施工总体处于中风险水平的因素显著表现在地质条件和盾构机械参数两方面,应对土质和施工条件通过注浆改善土体、及时调整盾构机械参数等有效措施降低风险,对于B2和B3则应加强监控使其处在可控水平上。

3.5 敏感性分析

通过敏感性分析,可以快速识别出在各状态下盾构下穿铁路施工诱发安全风险的关键影响因素,根据式(10)计算15个影响因素对叶节点T在较高风险等级下(T3、T4)的敏感度,敏感度越大,表示根节点对叶节点T的影响越大。计算得到了基于100个样本的所关注根节点的SPM均值如图5所示。

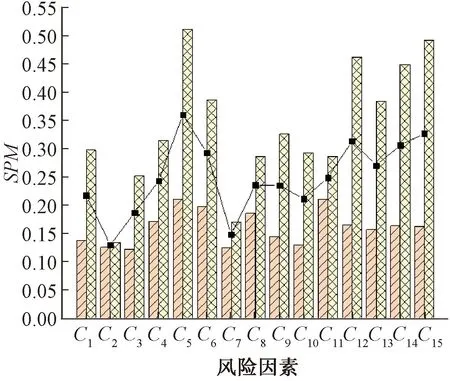
从图5可以看出,当T3时,即安全风险状态处在中风险时,轨道差异沉降C11、新建隧道埋深C5、穿越空间夹角C6、既有铁路等级C8四个因素的敏感度相对较大,对盾构下穿铁路施工安全风险处在3等级的影响较大;当T4时,新建隧道埋深C5、推进速度C15、土仓压力C12、推进力C14因素敏感度较大。两种风险状况下,较敏感的因素存在较大差异。总的来看,在施工前应该结合隧道与铁路相对位置及各自状况制定切实可行的施工方案,在施工过程中,盾构施工参数的对于系统处在高风险水平的影响会逐渐增强,要注意对施工参数及时进行分析调整和设计优化,控制和降低潜在风险,保证良好的施工管理水平。此外整体风险到达较高的水平时,15个影响因素的SPM均呈现显著增大变化趋势,T4时的各因子SPM基本为T3的1倍,也进一步说明了当系统面临越来越大的风险时,敏感性因素会起到重要影响,通过敏感性分析及时制定相关控制措施为风险管控提供了重要保障和决策支持。

3.6 风险诊断

基于贝叶斯网络的逆向推理技术,利用公式(12)可以计算各个致险因素对总体风险状况恶化发生工程安全事故的后验概率。假设事故发生安全风险等级处在较高P(T4)=1的情况下,图6给出了T4等级下15个影响因素后验概率的分布情况。

从结果可以看出,土体压缩模量C1、既有铁路等级C8两个因素的风险水平处于状态4的概率最大,接近100%,是最可能导致安全事故的直接诱因。其次土体黏聚力C2、内摩擦角C3、近接空间距离C7、土仓压力C12、推进力C14五个因素也处在相对较高的风险状态,总的来说土质条件致灾可能性最高。可以通过防灾设施的建立来降低风险,如护坡、挡土墙、防洪堤等,加强土地的稳定性和抗灾能力。为了减少寻因的盲目性,需要对初步诊断出的可能引起事故发生的最典型因素给予更多关注,因此在进一步的故障诊断过程中,可针对性地根据危险程度对这些因素进行第二轮的排查。也就是说,将C1=4作为给定新的证据输入到云BN模型中,实现下一个P(Ci|T4,C1=4)的故障诊断,以此类推将上一步的诊断结果作为下一步诊断的证据信息不断去进行多轮的诊断分析,直到找到最可能的致因组合,较好地控制住总体风险的演化。

4 结束语

1)提出基于云模型和贝叶斯网络的动态安全评价推理模型,并说明了基于该模型的盾构下穿铁路施工过程风险评估方法的具体步骤,主要包括:建立风险指标体系、贝叶斯网络构建、云模型获取先验概率、风险概率推理预测风险诊断等过程,为盾构下穿铁路近接施工系统实时安全决策分析提供支持。

2)基于大量文献和工程经验总结,从地质条件、隧道相关参数、既有铁路风险和盾构施工参数4个方面来识别影响盾构下穿铁路施工系统安全的风险因素,构建涵盖了15个影响因素的安全风险评价指标体系和评价标准。

3)结合工程实例,利用云贝叶斯模型进行推理,得到系统的风险水平为3等级(中风险)。通过敏感性分析可知盾构下穿铁路安全风险事件的发生与隧道埋深、直径,轨道沉降,施工参数密切相关,是安全控制的重点,并利用反向推理获得致险因素诊断概率值以指导施工。验证了该方法用于盾构下穿施工动态安全风险评价的实用性和优越性。