基于Bootstrap-Cpu 的机床进给机构装配过程能力评估方法＊

惠 阳 牛博雅 史建猛 梅雪松

（①中航西安飞机工业集团股份有限公司，陕西 西安 710089；②西安交通大学机械工程学院，陕西 西安 710048）

过程能力评估作为基于统计过程控制（statistical process control，SPC）的关键核心技术之一，不仅能够反映当前过程满足产品质量要求的能力，而且已经成为过程质量持续改善的重要手段[1]。在批量化机床进给机构装配过程中，受5M1E（人、机、料、法、测、环）因素影响，进给机构装配过程能力可能不足，会导致进给机构装配质量出现较大波动，甚至出现不合格产品。因此有必要对机床进给机构装配过程能力进行评估。

过程能力评估方法的实现建立在过程能力指数（process capability indices，PCIs）计算的基础上。最早关于PCIs 的研究主要包括第一代过程能力指数Cp[2]，第二代过程能力指数Cpk和Cpm[3-5]和第三代过程能力指数Cpk[6]。随后，过程能力评估方法在机械产品制造过程能力评估中得到了应用。Panse A等[7]通过过程能力指数和Cpk对反映齿轮箱质量的振动信号进行了分析，实现了对装配线末端齿轮箱检测过程能力评估。Bottani E 等[8]基于过程能力指数Cp和Cpk实现了制造车间装配线过程能力评估。吕立晓等[9]为验证六西格玛管理方法在某公司中低压液压缸制造质量中的效果，通过Cpk对改善前后的过程能力进行了评估，验证了所提方法的有效性。黄祖广等[10]针对加工过程短期能力评估问题，提出了一种基于统计过程的短期能力评估模型，并在数控车床加工轴工件实例中验证了模型的有效性。赵家黎等[11]提出基于熵权理论和模糊物元的改良多元过程能力指数，解决了汽车左前门外板的过程能力综合评价问题。上述研究均遵循统计过程控制的思想，通过质量观测样本估计质量特性的分布规律，然后根据分布规律选择或者构建不同过程能力指数来实现对机械产品制造过程能力的评估。但是这些过程能力评估方法的实现都需要有足够的样本数据作为支撑，不适用于机床进给机构装配过程小样本情况。

为此，美国斯坦福大学统计学教授Efron B等[12]在归纳、总结前人研究成果的基础上，基于模拟抽样统计推断思想提出了Bootstrap 方法，利用原始小样本数据，通过重采样来扩充样本容量来进行统计计算，从而实现了样本未知分布和小样本条件下的过程能力评估。Stoma P 等[13]利用传统过程能力指数Cp研究了基于Bootstrap 的过程能力评估方法，开发了一种基于引导法确定过程能力的程序，制定了生产过程能力置信区间的标准值，并通过实验分析指出基于Bootstrap 的过程能力评估方法比传统方法估计的结果更加准确，可以实现测量实验样本为10 的过程能力评估。Park C 等[14]研究了Bootstrap 方法在过程能力指数Cpk计算过程中的应用，并提出了Bootstrap 置信区间修正方法。Rao G S 等[15]利用Bootstrap 方法对非正态过程能力指数Cpkv的置信区间进行了估计。颜斌等[16]利用1/σ的无偏估计分别重新设计了过程能力指数Cp和Cpm，并利用Bootstrap 方法对它们的置信区间进行了估计，验证了所提方法的有效性，同时指出利用Bootstrap 方法可以给实际生产工作提供生产指导。然而，当前还未见到有关Bootstrap 方法在机床进给机构装配过程能力评估中应用的研究。

1 机床进给机构装配过程描述

图1 所示为机床进给机构装配过程，可以看出，机床进给机构装配过程是进给机构装配质量形成的过程，主要包括滑座安装、前后支撑座安装、线轨副安装、滚珠丝杠副安装和工作台安装等环节。在装配过程中，为了确保进给机构最终装配质量参数满足要求，就需要对若干装配环节的若干装配特征如直线度、平行度等进行测量和调整，直到该装配过程的装配质量参数满足精度要求才可进入到下一装配过程。然而此过程受到人（装配工人）、机（测量设备）、料（零件）、法（工艺方法）、环（环境状况）、测（测量方法）因素的影响，这些偶然或者随机因素是难以消除的，但它们会造成进给机构装配过程的装配质量出现波动，甚至出现不合格产品。因此，在批量化生产过程中，需要及时对机床进给机构装配过程能力进行评估。

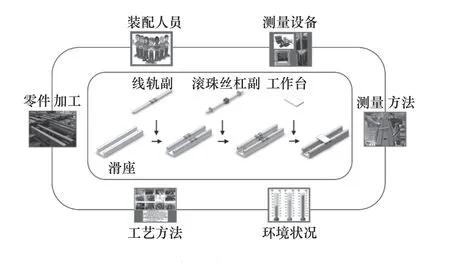
图1 机床进给机构装配过程

2 基本理论

2.1 Cpu 计算方法

在工程实际中，为了更好地对过程能力进行观察、测量和分析，通常使用可量化的PCIs 对具体过程能力进行描述。PCIs 是将过程的波动与输出的要求规格进行比较抽象而出的无量纲变量，在众多PCIs 中，Cpk描述了质量参数分布中心与规格中心不重合情况下的过程能力，并且因其易使用和易解释的特点在各个行业得到了广泛应用[3]。Cpk的计算公式为

式中：TU为质量参数的规格上限；TL为质量参数的规格下限； σ为质量参数标准差； µ为质量参数均值。

对于单侧规格，只有公差上限要求时，过程能力指数计算公式为

对于单侧规格，只有公差下限要求时，过程能力指数计算公式为

考虑到机床进给机构装配质量参数只有公差上限要求，可以利用Cpu对其过程能力进行估计。但Cpu的使用需要满足质量参数样本服从正态分布和足够样本进行参数估计的条件，并且统计过程控制中要求至少25 个以上的子组或者100 个以上的质量参数样本才能够建立可靠的控制限[17]。对于机床进给机构来说，其装配质量参数不服从特定分布，并且装配质量参数为小样本。因此，Cpu无法直接用于机床进给机构装配过程能力评估。

2.2 Bootstrap 计算方法

图2 所示为Bootstrap 方法的基本原理[14]。设A0={a1,a2,···,an}为一个不确定分布的长度为n的随机样本序列，tn表示A0统计量T的值。 那么Bootstrap 方法的基本原理可以描述为：首先，对样本序列A0进行B次有放回重采样，得到B个随机替换样本Ai∗（下标i表示第i次重采样，i=1,2,···,B），每个Ai∗={a1∗,a2∗,···,an∗}，称为Bootstrap 样本；其次，对每个Bootstrap 样本Ai∗计算其统计量T值，得到对应估计值，进而得到统计量T的Bootstrap 经验分布，记为tn∗={t1∗,t2∗,···,tB∗}；最后，在B足够大时，就可以用Bootstrap 经验分布代替实际分布，进而求出统计量T所有可能提供了一种近似。这样就可以通过Bootstrap 方法对小样本进行统计模拟，从而获得未知分布和未知参数的统计估计。

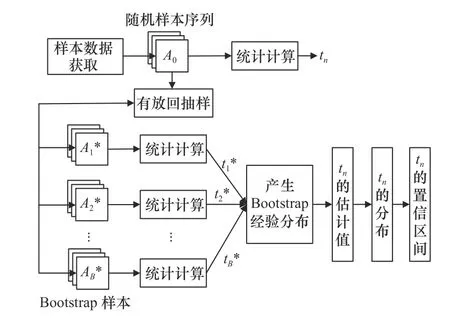
图2 Bootstrap 方法基本原理

对于样本量为n的样本序列，共有nn种可能的Bootstrap 样本，当n取较大值时这个数十分庞大。Efron 和Tibshirani 研究发现只需要得到1 000 组Bootstrap 样本就能得到准确的区间估计，因此后续在利用Bootstrap 方法进行计算时，B取1 000。经过不断的发展，Bootstrap 方法[18]又可以分为标准Bootstrap（standard bootstrap，SB）方法、百分位数Bootstrap（percentile bootstrap，PB）方法、t 百分位数Bootstrap（percentile-t bootstrap， PTB）方法和修正偏差后的百分位数Bootstrap（biased-corrected percentile bootstrap，BCPB）方法。这4 种方法均遵循图2 所示Bootstrap 方法基本原理，只是对区间上下限进行了不同估计。

下面以统计量T为例就上述4 种方法进行简单介绍。

（1）SB 方法

SB 方法建立在认为Bootstrap 经验分布tn∗={t1∗,t2∗,···,tB∗}近似服从正态分布的基础上。对于Bootstrap 经验分布的均值和标准差S∗，分别采用式（4）和式（5）计算得到。

进而得到T的100(1-α)%置信区间为

式中：Z(1-α/2)为标准正态分布的1-α/2百分位数。

（2）PB 方法

PB 方法通过将Bootstrap 经验分布tn∗={t1∗,t2∗,···,tB∗}按照从小到大排序，得到其第α/2 和1-α/2分位点，进而得到T的100(1-α)%置信区间为

（3）PTB 方法

PTB 方法建立在对PB 方法进行改进的基础上，使得得到的置信区间更加准确。该方法首先需要根据求得的Bootstrap 经验分布构造新的统计量t∗：

然后通过将t∗按照从小到大排序，得到其第α/2和1-α/2分位点，进而得到T的100(1-α)%置信区间为

（4）BCPB 方法

BCPB 方法考虑了随机反复抽样不均匀导致的Bootstrap 经验分布偏离原分布的情况。该方法首先求得Bootstrap 经验分布中小于tn的概率：

然后计算：

式中：Φ(·)为为标准正态分布的累积函数。

进而得到T的100(1-α)%置信区间为

3 基于Bootstrap-C pu的装配过程能力评估方法

设机床进给机构装配质量参数样本为y={y(1),y(2),···,y(N)}，N为质量参数样本数。下面通过引入Bootstrap 方法来对机床进给机构装配质量参数进行Cpu计算，进而构建了基于Bootstrap-Cpu的机床进给机构装配过程能力评估方法，该方法的主要步骤如下。

步骤1：对装配质量参数样本y={y(1),y(2),···,y(N)}进行有放回重复抽样，得到随机替换样本

步骤2：计算替换样本y∗的均值和方差，进而利用式（2）计算得到对应Cpu的估计值

步骤5：结合表1 过程能力评价参考表对Cpu进行分析，进而实现机床进给机构装配过程能力评估。

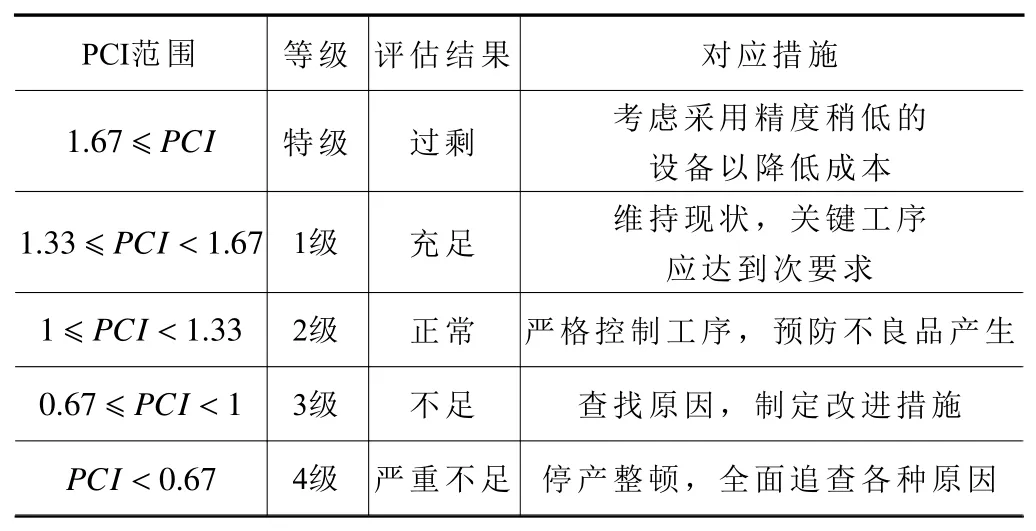
表1 过程能力评价参考表[20]

如果机床进给机构装配过程中存在n装配质量参数，只需要分别对每个装配质量参数执行基于Bootstrap-Cpu的装配过程能力评估方法，得到n个评估结果，最后综合这n个评估结果对机床进给装配过程能力进行评估。

4 实例应用

4.1 机床进给机构装配过程数据收集

图3 为某机床进给机构装配过程数据测量现场。在数据测量过程中，测量工具使用机床企业常用的杠杆千分表（型号：0-0.2，精度：0.002 mm）。同时，为了得到准确性测量结果，测量过程中装配质量参数取3 次测量结果平均值。表2 描述了该机床进给机构装配质量参数，主要包括工作台上表面与X轴平行度和工作台上表面与Y轴平行度。表3描述了某批次该机床进给机构装配质量参数样本数据。

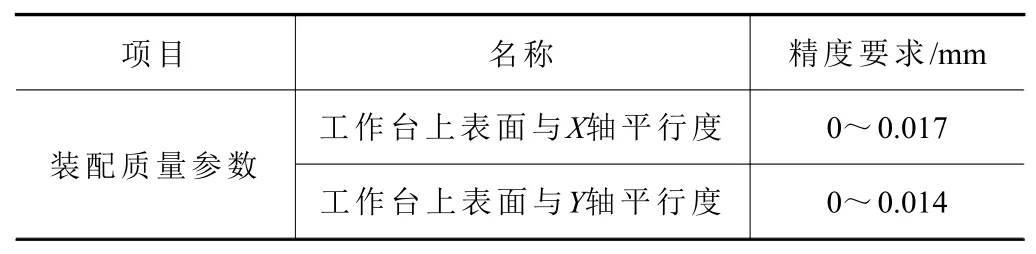
表2 某机床进给机构装配质量参数精度要求

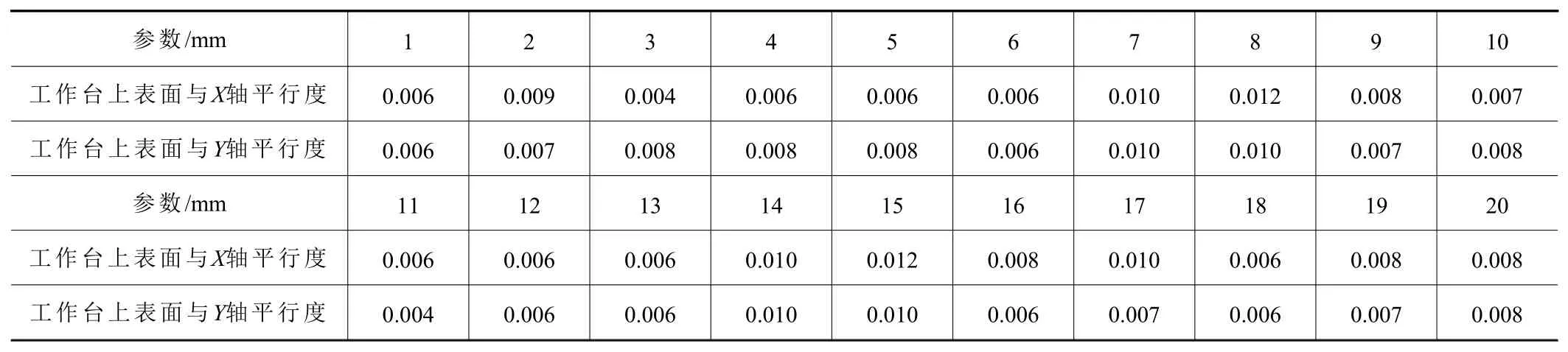
表3 某机床进给机构装配质量参数样本数据

图3 某机床进给机构装配质量参数数据测量现场

4.2 机床进给机构装配过程能力评估

由获取的机床进给机构装配过程测量数据，得到该批机床进给机构装配质量参数数据分布情况如图4 所示。可以看到，该批机床进给机构装配过程中工作台上表面与X轴平行度数据分布和工作台上表面与Y轴平行度数据分布均不服从正态分布，无法直接利用传统过程能力指数Cpu对进给机构装配过程能力进行评估。

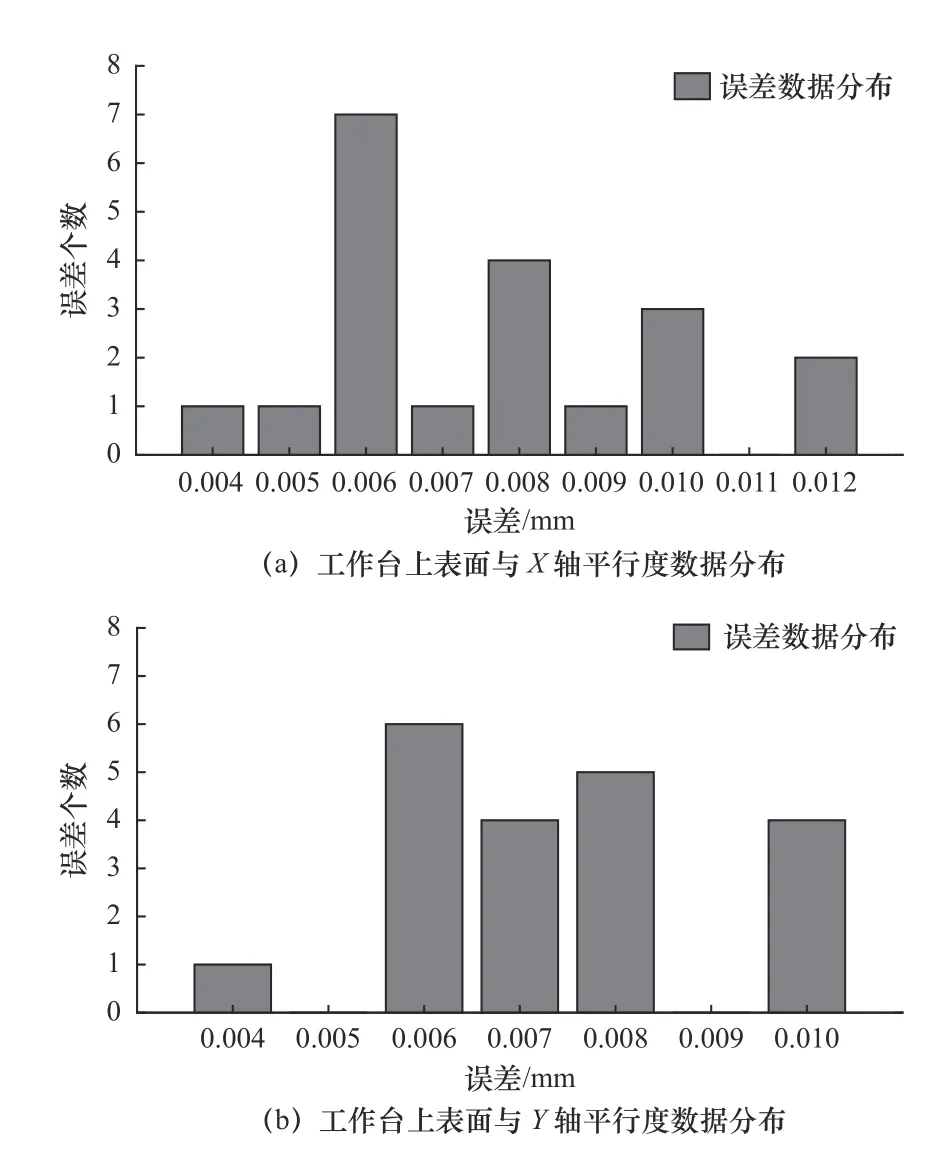
图4 机床进给机构装配质量参数数据分布

为此，首先设工作台上表面与X轴平行度数据统计量为Cpu1，工作台上表面与Y轴平行度数据统计量为Cpu2，采用章节3 提出的基于Bootstrap-Cpu的进给机构装配过程能力评估方法对该批机床进给机构装配过程能力进行评估。

其次，分别对现有20 组工作台上表面与X轴平行度数据和工作台上表面与Y轴平行度数据进行有放回抽样，抽样1 000 次，分别得到它们的1 000 组Bootstrap 样本。利用式（2）计算工作台上表面与X轴平行数据的1 000 组Bootstrap 样本的Cpu1估计值，得到统计量Cpu1的Bootstrap 经验分布如图5 所示，可以看到在中，值小于1 的百分比为0.6%，值大于等于1 的百分比为99.4%；同时，利用式（2）计算工作台上表面与Y轴平行度数据的1 000 组Bootstrap 样本的Cpu2估计值，得到工作台上表面与Y轴平行度数据统计量Cpu2的Bootstrap 经验分布如图6 所示，可以看到在计算结果中，值小于1 的百分比为1%，值大于等于1 的百分比为99%。显然，Bootstrap 经验分布和中各Bootstrap 样本Cpu估计值大于等于1 的百分比均达到了99%，说明该批机床进给机构装配过程能力可能是足够的。

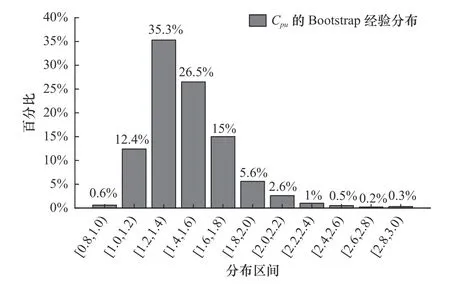
图5 工作台上表面与X 轴平行度数据统计量Cpu1的Bootstrap 经验分布

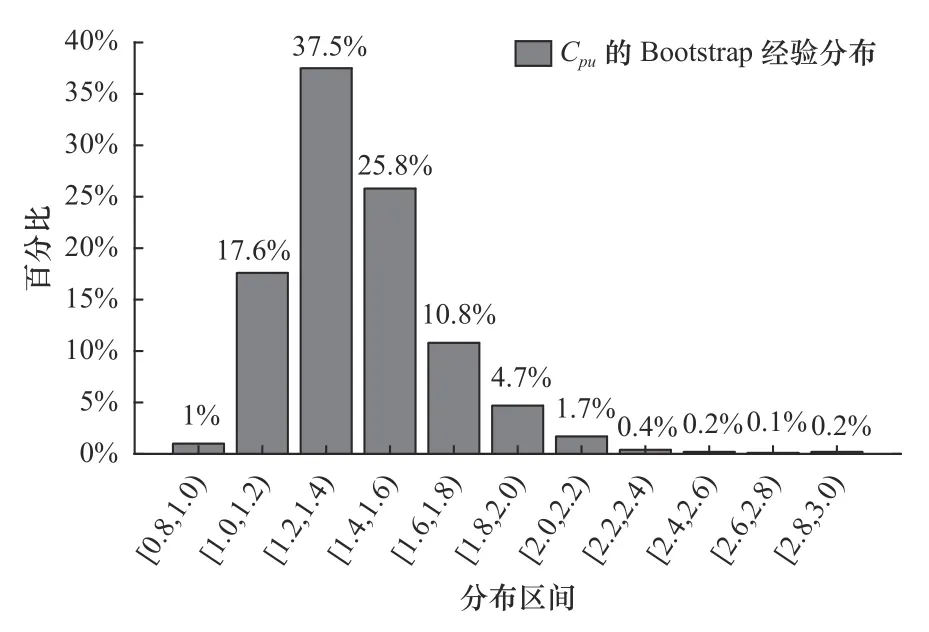
图6 工作台上表面与Y 轴平行度数据统计量Cpu2的Bootstrap 经验分布

最后，按照式（6）、式（7）、式（9）和式（14）进行Cpu95%置信度下的SB、PB、PTB 和BCPB 置信区间计算，得到基于Bootstrap-Cpu的进给机构装配过程能力指数计算结果，见表4，这里引入覆盖率（Cov）的概念来表示真值落在置信区间的频率值。由表4 可知，工作台上表面与X轴平行度数据Cpu估计值Cpu的Bootstrap 估计值对应的SB、PB、PTB 和BCPB 置信区间下限值均大于1，4 种置信区间都有着较高的覆盖率（93%、95%、93% 和95%），并且置信区间长度最大不超过1.03；工作台上表面与Y轴平行度数据Cpu估计值Cpu的Bootstrap 估计值对应的SB、PB、PTB 和BCPB 置信区间下限值均大于1，4 种置信区间都有着较高的覆盖率（93%、95%、94% 和94%），并且置信区间长度最大不超过1.1。

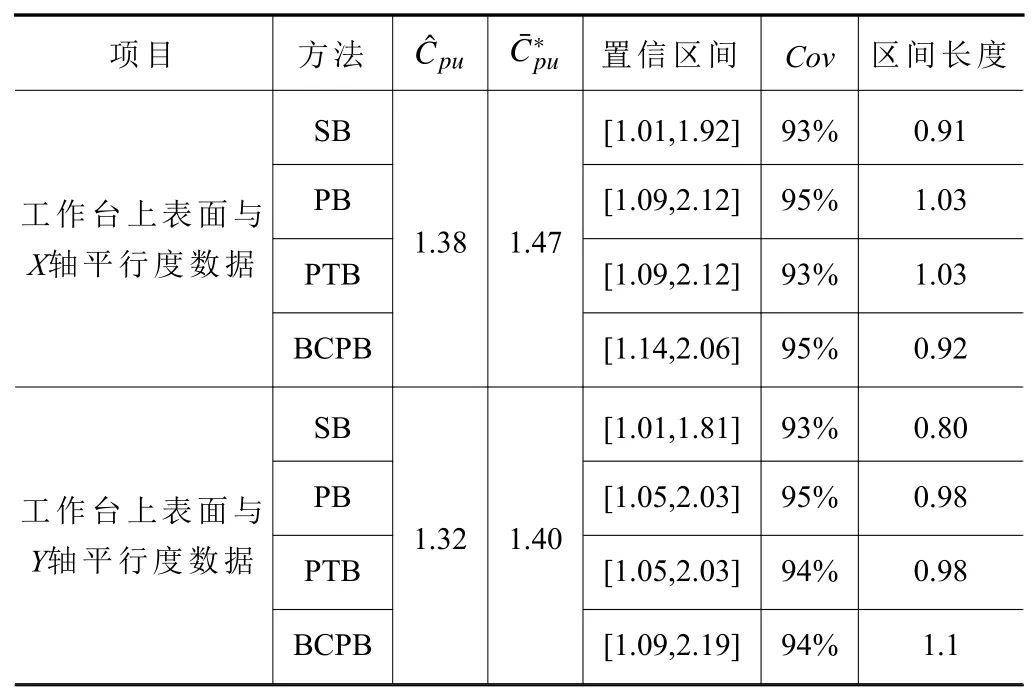
表4 基于Bootstrap-Cpu 的机床进给机构装配过程能力指数计算结果

显然，在95% 置信度条件下，工作台上表面与X轴平行度数据和工作台上表面与Y轴平行度数据Cpu的4 种Bootstrap 置信区间（SB、PB、PTB 和BCPB）计算结果没有显著性差异，它们对应的4种置信区间下限值均大于1，对应的值分别为1.47 和1.40，且工作台上表面与X轴平行度误差数据最大置信区间长度为1.03 时对应的最小覆盖率为93%，工作台上表面与Y轴平行度误差数据最大置信区间长度为1.1 时对应的覆盖率为94%。因此，该批机床进给机构装配过程能力是足够的，其装配质量波动较小。

5 结语

本文在对过程能力指数Cpu和Bootstrap 方法进行分析的基础上，构建基于Bootstrap-Cpu的机床进给机构装配过程能力评估方法，得到了95% 置信度条件下进给机构装配质量参数误差数据最大置信区间长度均大于1、最小覆盖率均大于93%的结论，表明实例中的该批机床进给机构装配过程能力是足够的，进而实现了机床进给机构装配过程能力评估。